基于压力拱发展规律的隧道初次支护时机研究

王立华, 刘源, 孙捷城, 李洁, 吕显州, 王渭明

(1.山东科技大学 土木工程与建筑学院, 山东 青岛 266590;2.济南轨道交通集团有限公司, 山东 济南 250014;3.山东高速建设管理集团有限公司, 山东 济南 250014;4.山东科技大学 地球科学与工程学院, 山东 青岛 266590)

0 引言

在隧道开挖过程中,压力拱的形成对隧道的稳定性保障具有重要作用[2]。针对该问题,众多学者展开了大量研究。刘燕鹏[3]在隧道围岩破坏过程中不同开挖方法下,对压力拱的分布范围及其动态发展规律进行研究,得出隧道塌方过程中,压力拱拱体范围随隧道塌落高度的变化而改变的结论。叶飞等[4]根据隧道开挖现状,分析了压力拱的发展规律,从理论上推导了初始压力拱和坍塌压力拱的范围,并且分析了压力拱动态发展过程中的影响因素。侯伟名[5]根据现有压力拱理论对特殊地层昔格达地层中隧道开挖时围岩的失稳形态和应力变化规律进行研究,分析了隧道开挖过程中压力拱的动态发展过程与最终形成状态,探究了隧道开挖过程中昔格达地层的发展状态。以往对于压力拱的研究基本都是基于隧道横截面方向的压力拱形态的分析[6],对于压力拱形态在隧道开挖过程中的变化分析较少,但是其特征形态是随着开挖进程动态发展的,因此从纵断面方向对隧道围岩状态进行研究是有必要的。

压力拱的形成对于充分发挥围岩自承能力具有支撑作用[7]。基于新奥法的共同作用原理强调充分发挥围岩自承能力的同时,需要通过各类支护方式适时加固围岩[8-9],因此在对围岩支护时应根据围岩条件,合理确定支护的施作时间,保证围岩与支护共同作用的有效发挥。在此方面,唐苗[10]采用物理模型试验和数值模拟相结合的方法,分析了马蹄形隧道围岩塑性区对压力拱高度的影响,并将压力拱理论应用于隧道围岩稳定性分析,从压力拱理论的角度探究了隧道衬砌施作时机与压力拱成拱之间的关系。王睿等[11]提出将隧道开挖后围岩产生松动圈的时刻作为施作初期支护的最佳时间,分析了隧道围岩应力变化和衬砌变形规律。路军富等[12]采用围岩变形基本稳定速率作为判定指标分析高铁黄土隧道二次衬砌的施作时机。Sharifzadeh等[13]通过采用应力释放法和参数弱化法分析初期支护施加时机对引水隧道开挖损伤区范围的影响。当前研究多通过应力释放率确定支护时机[14],为了更加直观地反映初期支护对于开挖面上方围岩变形的约束能力,本文引入位移完成率衡量围岩受开挖扰动程度,通过所建立的位移完成率和应力释放率的对应关系,获得最优支护时机。

本文通过有限元软件FLAC3D对济莱高铁隧道开挖过程进行动态模拟分析,研究隧道开挖过程中围岩压力的变化规律及隧道变形机制,分析压力拱的动态发展过程,得出隧道纵截面压力拱形态特征图,并在此基础上提出隧道初期支护施作时机的确定方法,以期为类似工程条件下的隧道支护时机的优选提供参考。

1 工程概况及模型建立

1.1 工程概况

济南至莱芜高速铁路位于山东省中部,线路西起济南市济南东站,终于钢城区钢城站。济莱高铁沿线地貌分区图如图1所示。本线西端通过济南枢纽连接济滨、石济、济青等高速铁路,南端远期延伸至鲁南高铁。

图1 济莱高铁沿线地貌分区图Fig.1 Landform zoning map along the Jilai high-speed railway

本文中以济莱高铁宅科隧道DK36+530～DK36+590段为研究背景,隧道埋深为40～105 m,围岩级别为Ⅳ级,其断面尺寸示意图如图2所示。隧址区地处山东省中部隆起区,进口段临近宅科水库特大桥,出口处临近凤落峪中桥。构造侵蚀、剥蚀低山地貌,覆盖层厚度为30～130 m,冲沟较发育。

图2 宅科隧道断面尺寸示意图Fig.2 Schematic diagram of section size of Zhaike Tunnel

1.2 模型建立

本文模型建立过程中,对岩土体中包含的节理等非连续均匀介质进行简化,采用强度折减的方法进行数值分析。根据圣维南原理,结合宅科隧道现场实际,建立三维模型如图3所示,模型长度为70 m,宽度为60 m,高度为55～75 mm,计算模型共有53 553个单元,为了减小边界效应的影响,计算时上边界为自由面,4个侧面为水平约束面,底部为全约束平面。

通过实验发现,当随机森林中树的个数为200时,每棵树的深度在10之后分类准确率会趋于稳定,对于行为数据集分类准确率达到很好的效果。

隧道地层自上而下依次为碎石土、泥质灰岩、灰岩,围岩及支护计算参数见表1。模拟中本构模型采用摩尔-库伦模型,支护结构选取各向同性弹性本构体,锚杆采用cable单元,衬砌采用厚度为30 cm实体单元,采用三台阶开挖法,开挖进尺根据初期支护钢架间距确定,本模拟中支护钢架距离设置为4 m。

表1 围岩及支护计算参数Tab.1 Calculation parameters of surrounding rock and support

为了更准确地模拟现场实际地质情况,在隧道围岩特布置5个路径并设置测线提取相应位置的应力,从而分析隧道在不同埋深条件下围岩应力变化情况,测线L1、L2、L3、L4、L5应力监测路径如图4所示。

图4 隧道围岩应力监测路径Fig.4 Stress monitoring path of surrounding rock of Tunnel

2 压力拱动态演化分析

2.1 围岩应力分析

隧道开挖后,随着二次围岩应力的不断调整,围岩竖向应力产生了显著变化,隧道开挖后竖向应力云图如图5所示。从图中可以发现,隧道拱顶的荷载通过拱腰传递至拱脚,使得拱脚位置的应力大于处于同一高度下围岩的应力,由此可知,隧道开挖使得围岩中产生压力拱现象。

图5 隧道开挖后竖向应力云图Fig.5 Cloud map of vertical stress after tunnel excavation

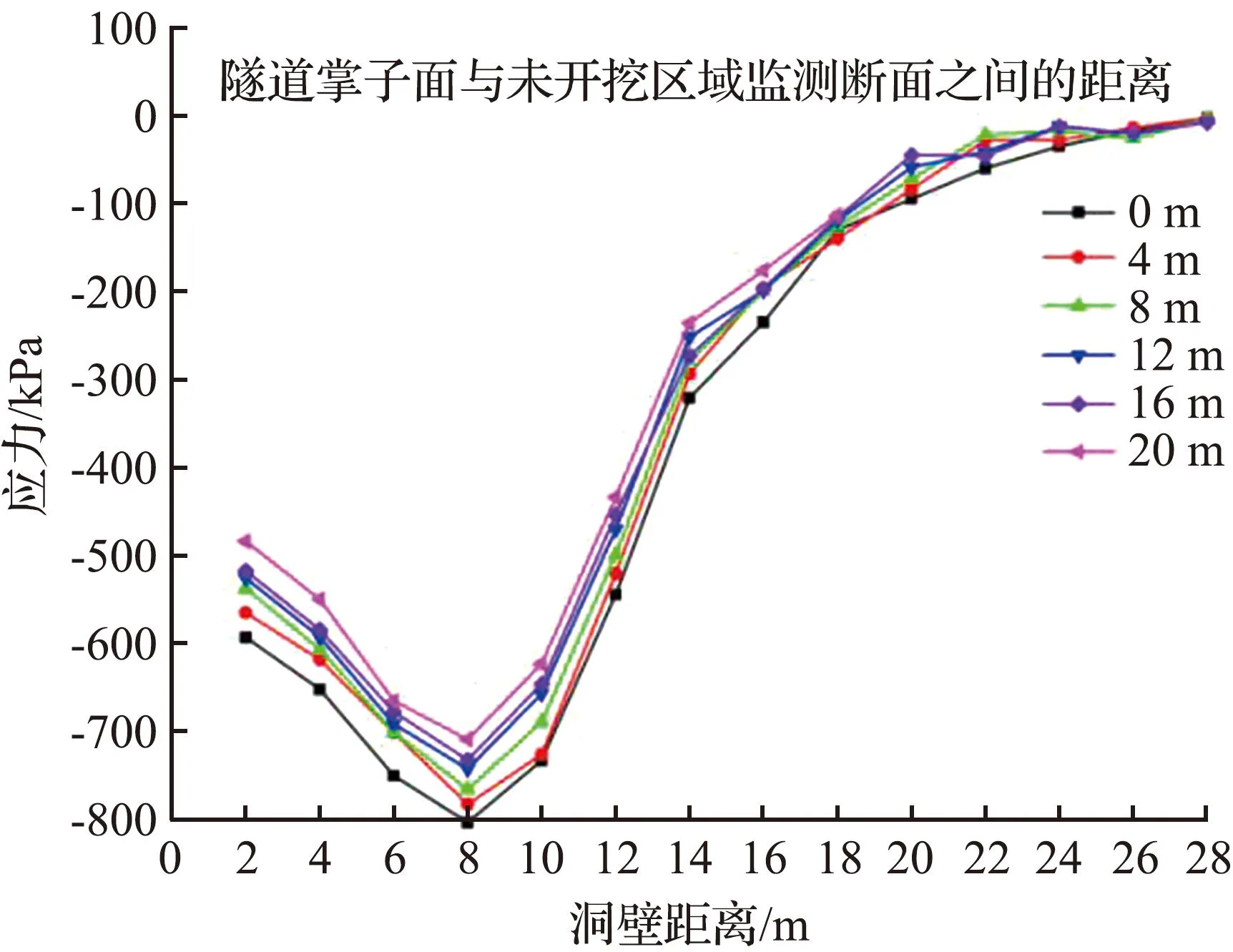
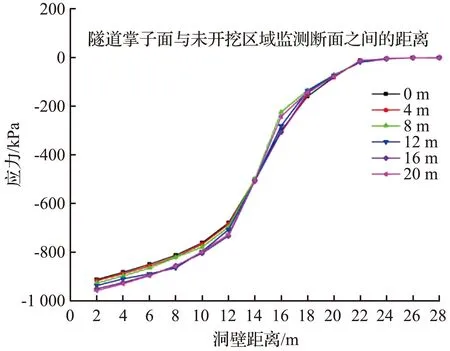
隧道开挖至24 m时测线L1围岩应力变化情况如图6所示。由图6可知,洞壁距离一定时,开挖断面上方围岩受扰动程度远大于未开挖断面。洞顶上方2～6 m高度范围内环向应力增大,且于6 m位置处环向应力达最大值-394.61 kPa。拱顶8～20 m范围内径向应力与原岩应力相比基本无变化,随着洞顶距离的增大环向应力逐渐减小为0。径向应力受扰动的深度约为8 m,而环向应力增大的幅度为20 m,由此可知隧道拱顶以上20 m范围内的围岩均参与成拱效应。

(a) 径向应力

(b) 环向应力图6 测线L1围岩应力的变化Fig.6 Stress change of surrounding rock of survey line L1

根据压力拱边界判定[15-18]可知,其内边界位于最大主应力出现最大值处,因此该隧道压力拱内边界位于洞顶上方4 m处。压力拱外边界判定为切向应力减小到原岩应力与环向应力比值为0.9处,即隧道上方18 m位置,约位于隧道上方1.4D位置处(D为隧道截面宽度)。由此可知,隧道拱顶位置在1.4D范围内的围岩参与成拱效应,承担着隧道拱顶上方的围岩荷载。

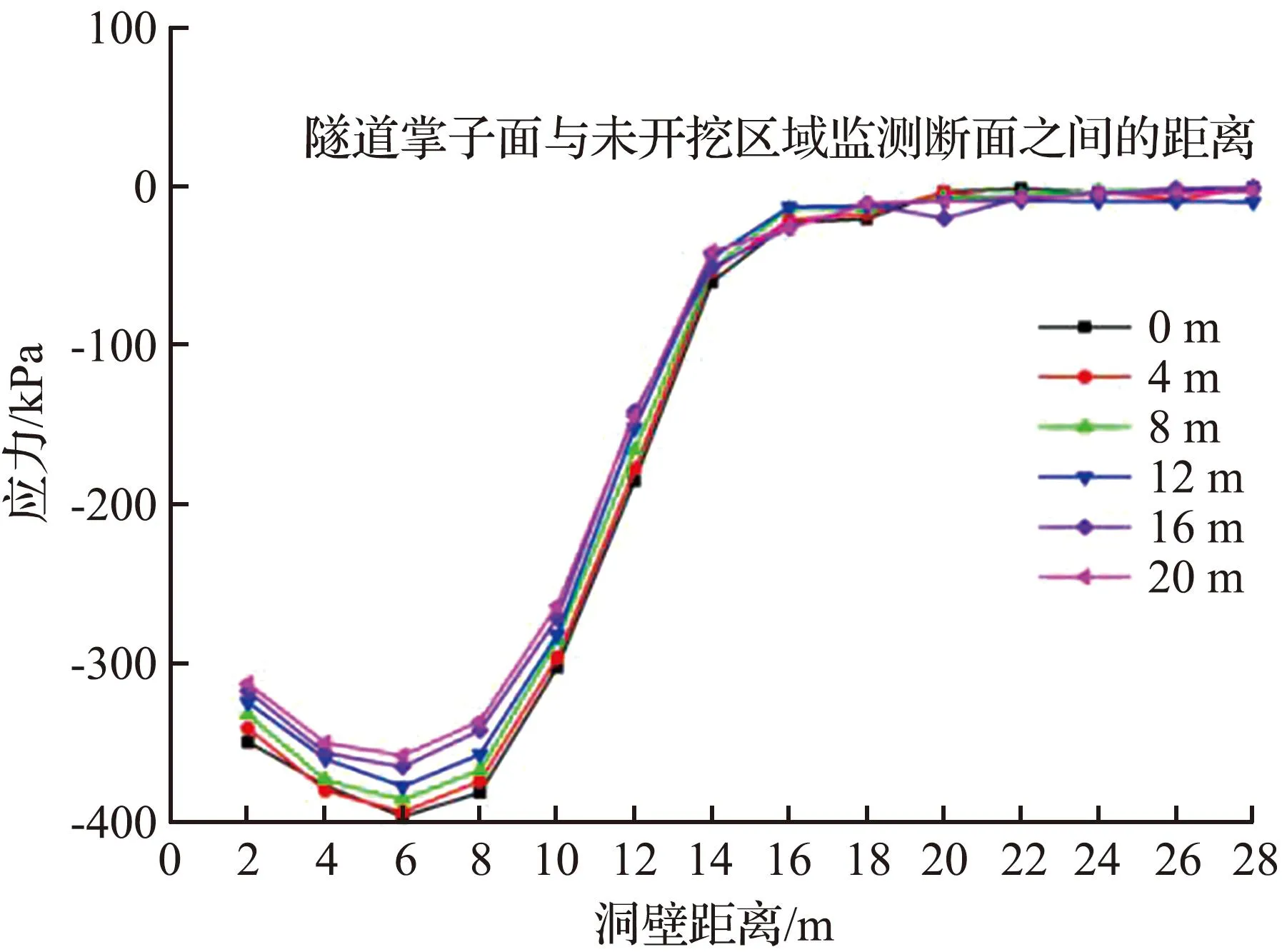
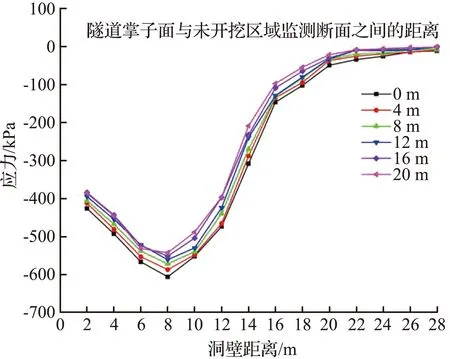
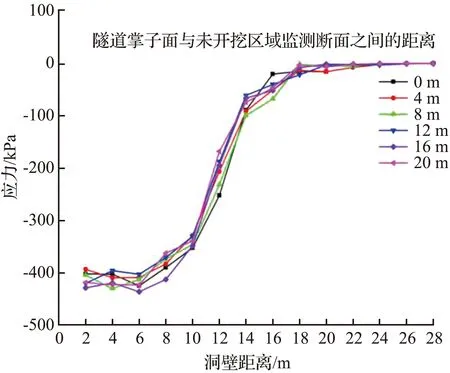
测线L2、L3围岩应力的变化分别如图7、图8所示。由图7可知,在隧道拱肩位置2～8 m受隧道开挖扰动影响较大,在距离隧道上方8 m位置的围岩应力最大,径向应力最大值为-499.67 kPa,环向应力最大值为-605.33 kPa。可见,随着掌子面距离监测断面(Y=24 m)不断接近,各监测点应力值不断增加并于相距为0时达最大值,表明隧道压力拱的发展过程是一个动态演化过程,会随着隧道的开挖逐渐向外侧扩展。

(a) 径向应力

(b)环向应力图7 测线L2围岩应力的变化Fig.7 Stress change of surrounding rock of survey line L2

(a) 径向应力

(b) 环向应力图8 测线L3围岩应力的变化Fig.8 Stress change of surrounding rock of survey line L3

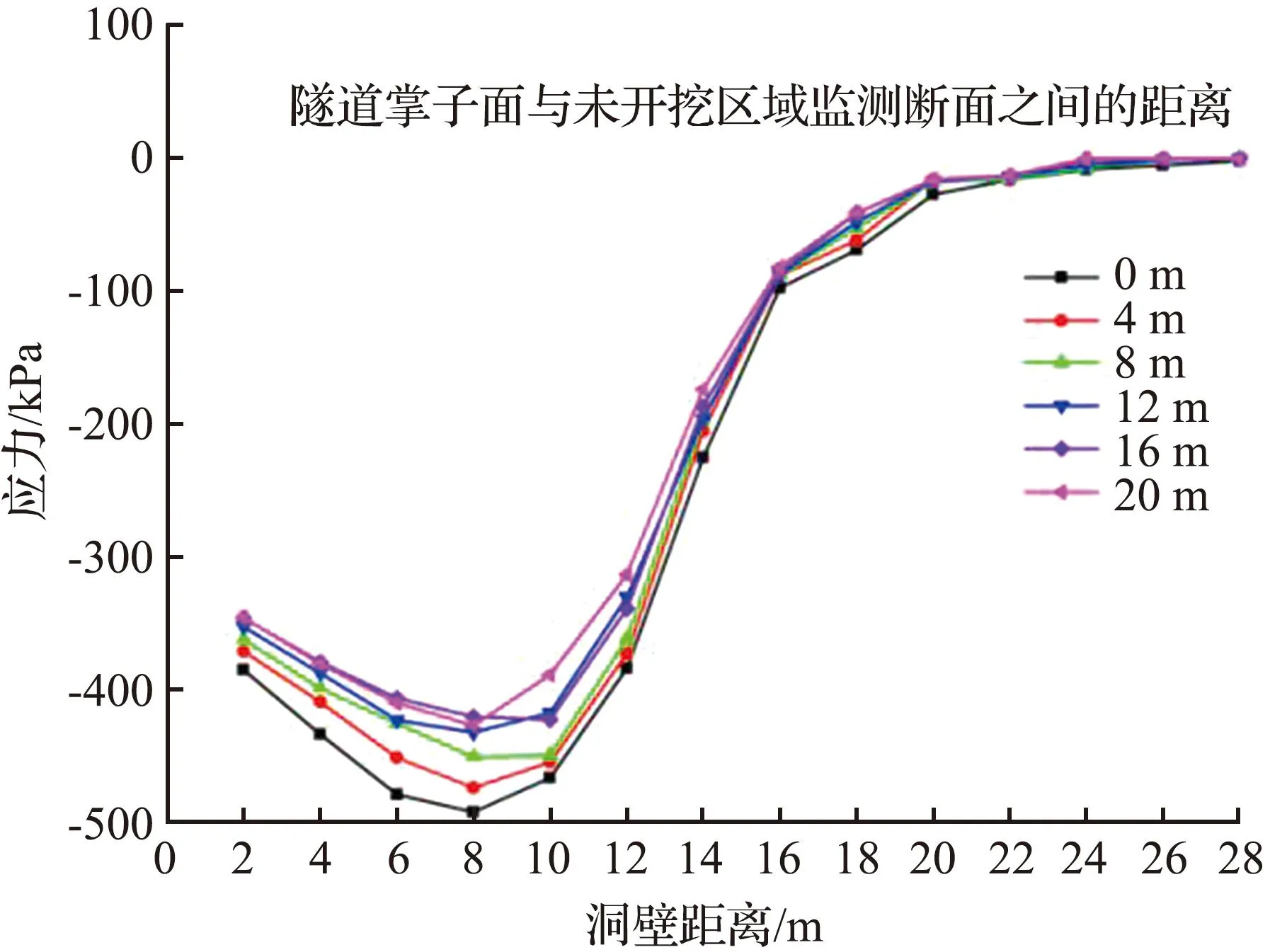
由图8可知,对比测线L2和测线L3可知,测线L3的围岩应力要大于测线L2的,且测线L3环向应力最大值出现在距离洞壁8 m位置处,说明在隧道围岩中不同路径应力重分布的幅度不同,并且靠近拱脚位置的围岩应力要大于其他位置的。

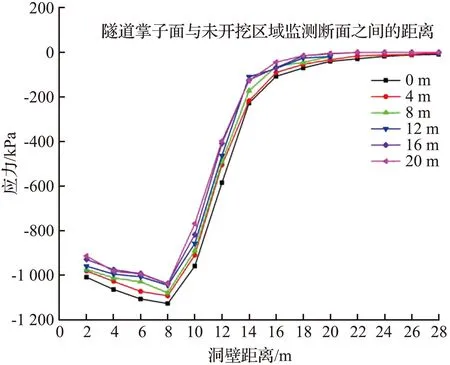
隧道拱脚部位测线L4围岩应力的变化如图9所示,与测线L1、L2、L3相比测线L4的应力值明显增大,说明拱脚部位主要承担来自压力拱上方围岩的荷载。从图9(b)中可以看出,监测断面最大围岩压力为-1 385.25 kPa,距洞壁12 m处,其值远大于L1、L2、L3相同位置的环向应力,围岩环向应力的峰值随着远离隧道洞壁方向逐渐减小,在距离隧道洞壁15 m处围岩应力迅速减小,然后逐渐恢复至原岩应力大小。

(a) 径向应力

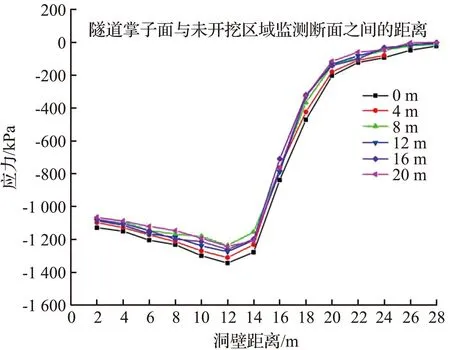
(b) 环向应力图9 测线L4围岩应力的变化Fig.9 Stress change of surrounding rock of survey line L4

仰拱处测线L5围岩应力的变化如图10所示。由图10可见,径向应力受开挖扰动的范围约为拱脚右侧12 m范围内,12 m范围以外的区域急剧减小逐渐恢复为0。从环向应力的变化趋势可以看出,隧道开挖影响在监测断面上方8 m处出现转折点,8 m以外范围内的围岩应力逐渐减小,并且各点的环向应力和径向应力均远大于其他测线的测量结果,24 m处围岩环向应力与径向应力均减小为0,即恢复至原岩应力大小。

(a) 径向应力

(b) 环向应力图10 测线L5围岩应力的变化Fig.10 Stress change of surrounding rock of survey line L5

由此可见,隧道仰拱靠近拱脚部位在0～24 m(即1.8D范围内)的围岩参与成拱效应,承担着隧道拱部上方的围岩荷载。这是由于围岩主应力方向受到隧道开挖影响产生偏转,最大主应力方向逐渐从竖直方向偏转至水平方向,隧道围岩中出现具有拱的力学特征的封闭环形应力,使得围岩拱体上方的荷载传递至隧道拱脚处围岩。在施工过程中压力拱范围是逐渐扩展的,并且在仰拱下方22 m范围内能够形成稳定的压力拱。

2.2 压力拱特征分析

根据隧道压力拱拱体处于环向应力升高区,隧道压力拱的外边界为小于原岩应力10%的点所组成的边界线[19],将5条测线所得结果与隧道外廓描点连线得到压力拱横截面断面特征形态图,隧道横截面压力拱形态特征图如图11所示,图中灰色填充区域为压力拱范围,所得到的压力拱范围是一个分布在隧道周围的封闭环形的拱形区域,在边墙和拱脚处的范围最大,拱顶区域分布范围较小。

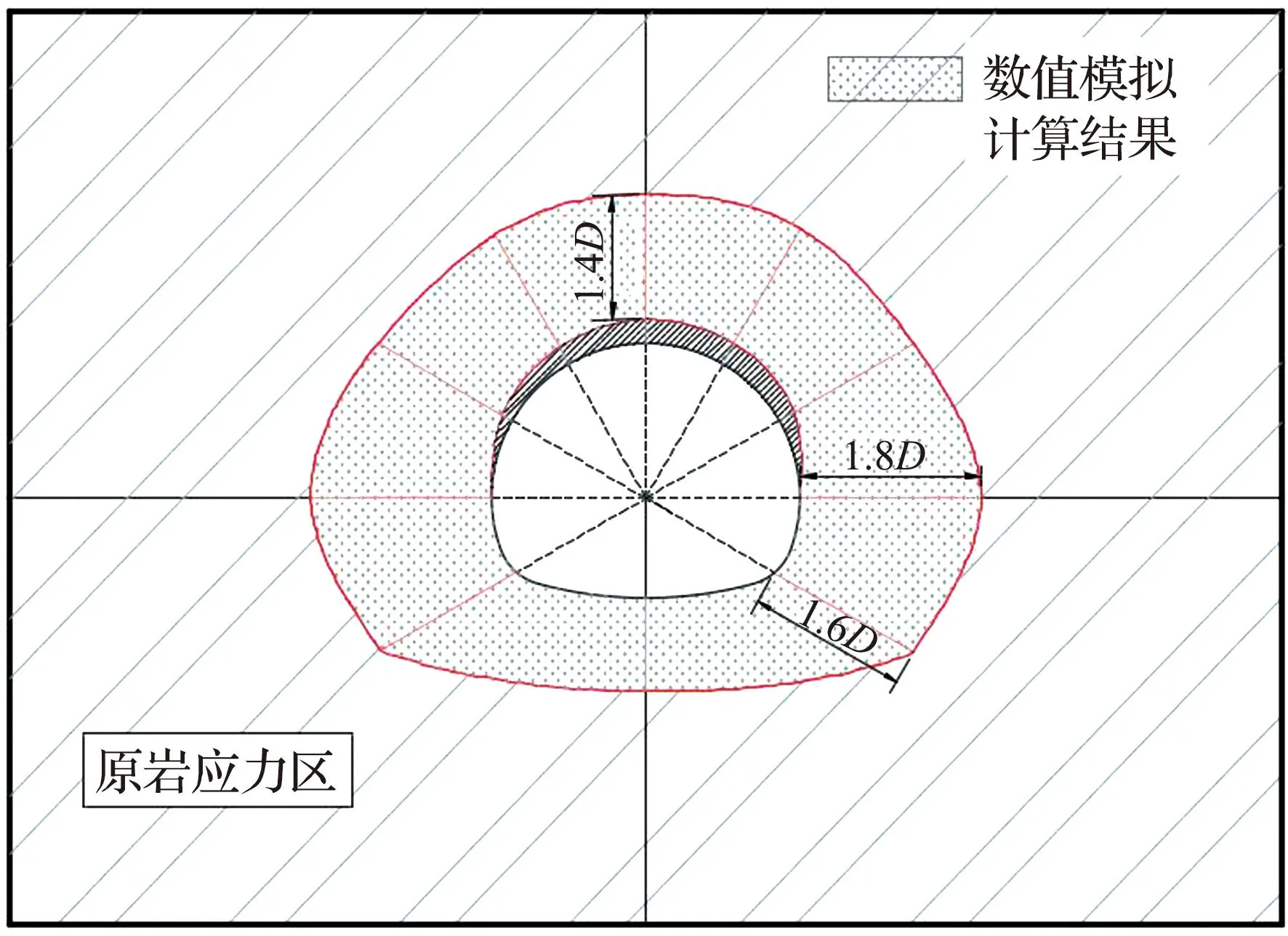
图11 隧道横截面压力拱形态特征图Fig.11 Shape characteristic diagram of tunnel cross-section pressure arch

隧道纵截面压力拱形态特征图如图12所示。由图12可知,在隧道开挖过程中拱顶上方形成临空面,拱顶位置围岩在重力的作用下产生破裂,使得该位置形成了松动区,掌子面前方的围岩通过自身的变形调节作用对周围岩体形成一定的约束能力,在拱部位置形成压力拱,且稳定拱体的形成贯穿开挖全过程。随着中台阶和下台阶逐步开挖,拱体范围逐渐扩大至仰拱部位[15]。开挖面上方依次形成了压力拱区域和原岩应力区2部分。

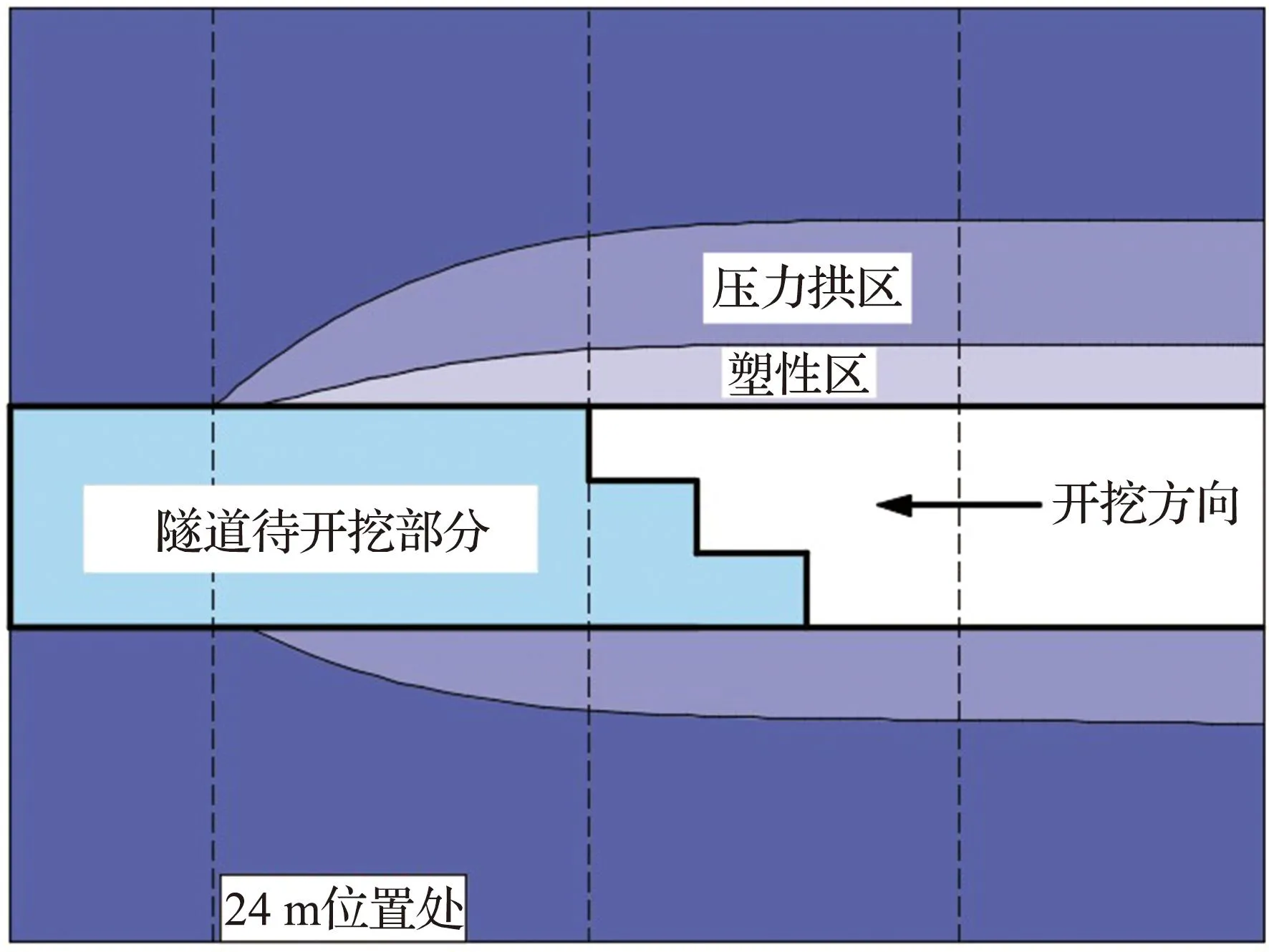
图12 隧道纵截面压力拱形态特征图Fig.12 Shape characteristic diagram of longitudinal section pressure arch of tunnel

经过多次的调节作用,与隧道外侧一定距离之外的围岩逐步趋于稳定状态,能够形成较为稳定的压力拱承担上方围岩传递来的压力[16]。在对隧道结构进行加固时,应当充分考虑隧道的围岩应力变化特点,从而对隧道围岩失稳区进行有效的加固处理,充分发挥围岩自承能力。

3 山区隧道开挖支护时机确定

3.1 初次支护时机判据选择

为了研究不同支护时机影响下围岩的受力状态及支护结构力学行为,本文以济莱高铁宅科隧道为背景按照围岩应力释放率为50%～100%时施作初期支护进行分析,数值分析工况见表2。

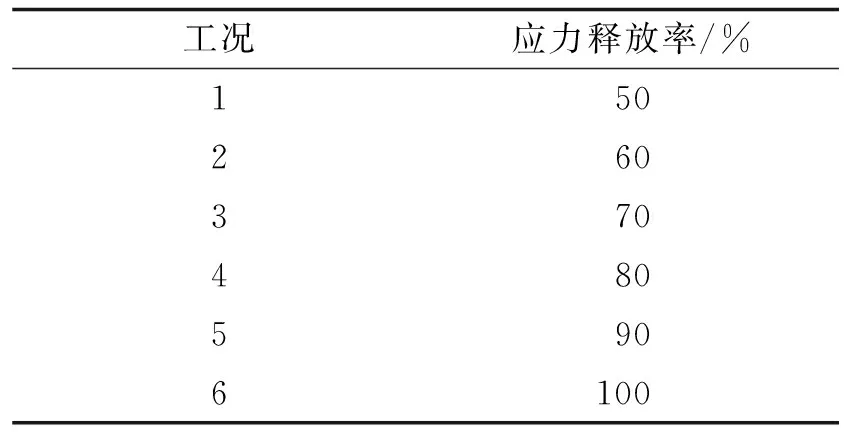
表2 数值分析工况Tab.2 Numerical analysis conditions

研究山区高铁隧道开挖应力释放时,地应力的释放过程一般采取空间反向荷载施加法[20],即根据工程实际情况设定将模型边界选定为隧道宽度的3～5倍来消除边界效应的影响,通过对隧道上方的各个节点的节点反力进行计算,然后在进行隧道开挖模拟时对该节点反力的1～a(a为不大于1的值)进行计算,最后将其反向施加在该节点上进行数值分析,待初期支护施作后释放剩余的节点力,以此具体实现模拟隧道开挖后围岩应力逐步释放的过程。

3.2 支护时机对于围岩塑性区的影响

通过对比分析在应力释放率不同时围岩塑性区分布情况,研究应力释放率对围岩变形破坏的影响,得到的不同应力释放率条件下塑性区分布状态,如图13所示。由图13可见,在不同应力释放率条件下的围岩塑性区分布形态相似,主要集中分布于隧道洞周区域,并且在隧道拱顶位置出现明显的塑性区面积增大的现象。

(a) λ=0.5

(b) λ=0.6

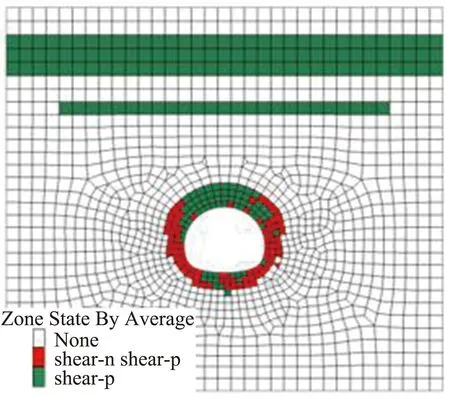
(c) λ=0.7

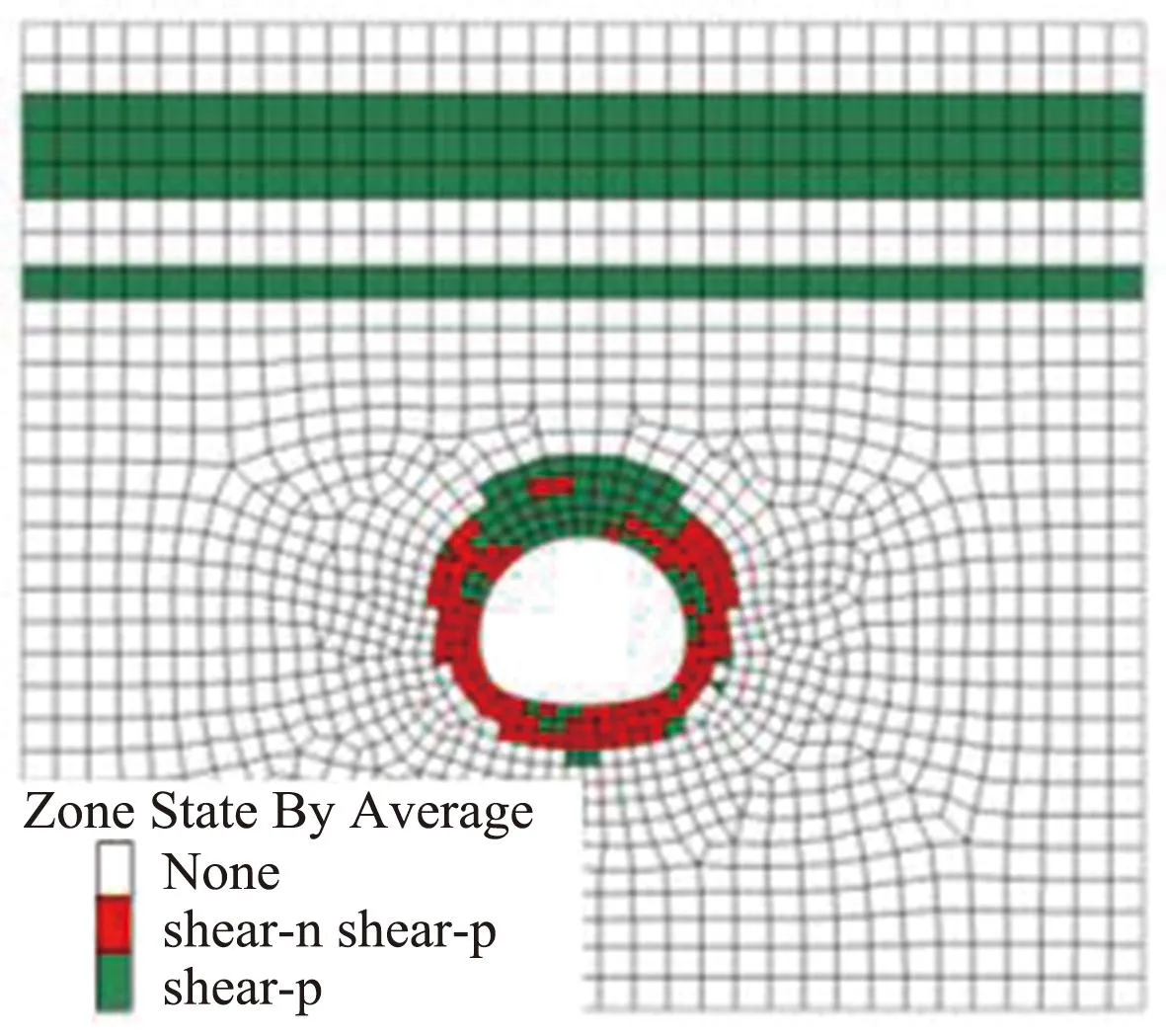
(d) λ=0.8

(e) λ=0.9

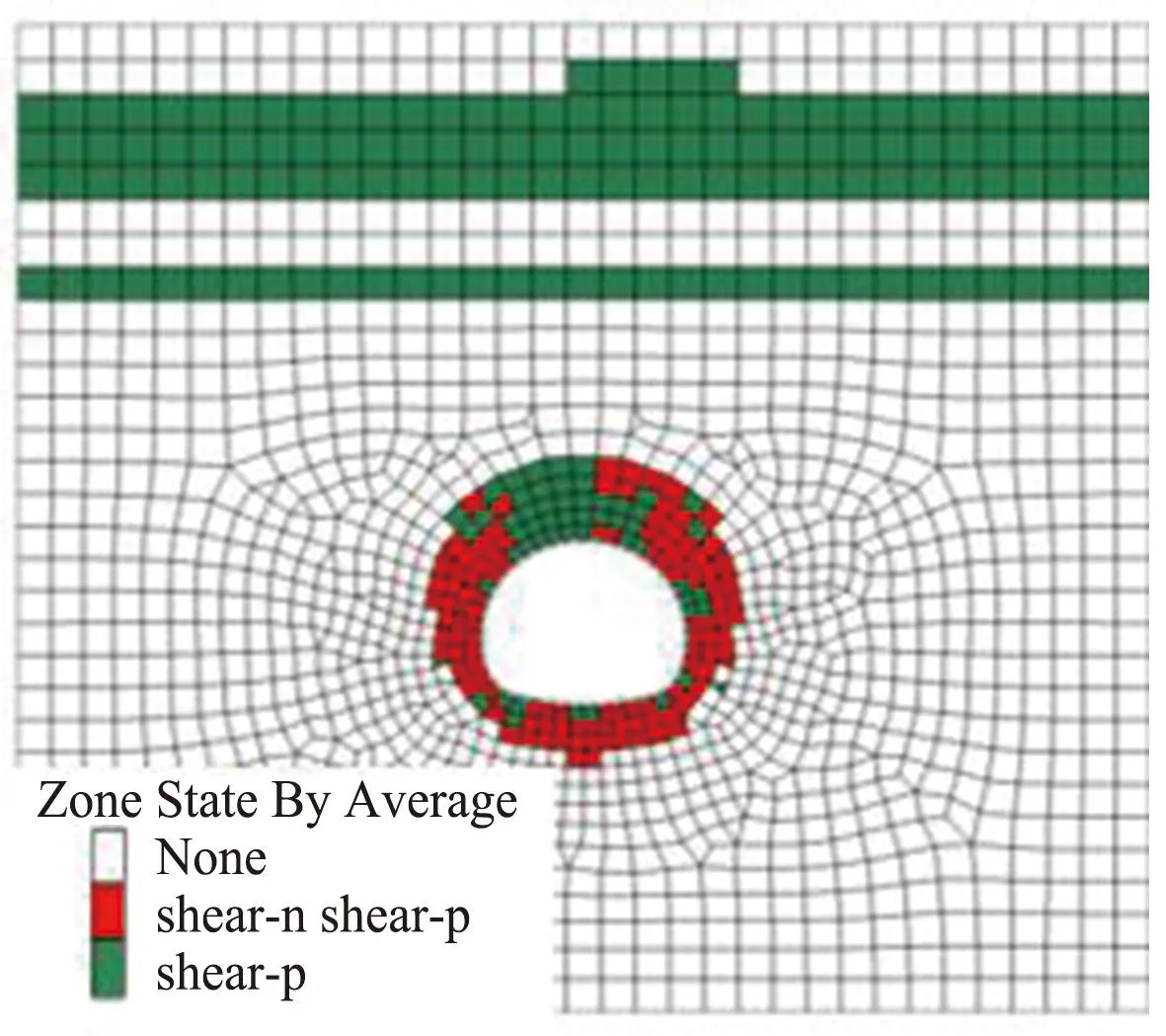
(f) λ=1.0图13 不同应力释放率λ条件下塑性区分布状态图Fig.13 Distribution state diagram of plastic zone under different stress release rates λ

塑性区体积率随应力释放系数的变化如图14所示。由图14可以发现,在对塑性区体积率进行计算时,随着应力释放率的增大和开挖断面逐渐向前推进,围岩的塑性区范围不断增大,此时隧道围岩主要受到剪切破坏。随着隧道开挖荷载释放率的增大,塑性区的体积也在逐渐增大,当隧道开挖荷载释放达到90%时,围岩的塑性区体积率迅速增大,因此需要在开挖荷载释放为70%和80%时施作初期支护,能够尽量减小围岩变形,维持隧道结构的稳定性。

图14 塑性区体积率随应力释放系数的变化Fig.14 Plot of the volume rate of plastic zone as a function of the stress relief coefficent

3.3 支护时机对于隧道变形影响分析

根据上述塑性区体积率和塑性区分布进行分析,得到最佳支护时机为应力释放率的70%和80%。隧道开挖过程中的应力释放率为70%、80%时的围岩位移如图15所示。从图15中可以看出,掌子面尚未开挖至隧道监测断面时,各监测点均已出现不同程度变形,随着掌子面逐渐向隧道监测断面推进,各监测点的变形逐渐增大,通过一段距离后位移增量逐渐减小,此时位移达到最大值,围岩趋于稳定状态,即压力拱整体形成,围岩产生较大变形的危险点分别是拱顶和拱肩位置这2个点,对于支护结构的分析时应当从这2个最危险位置点着手考虑。

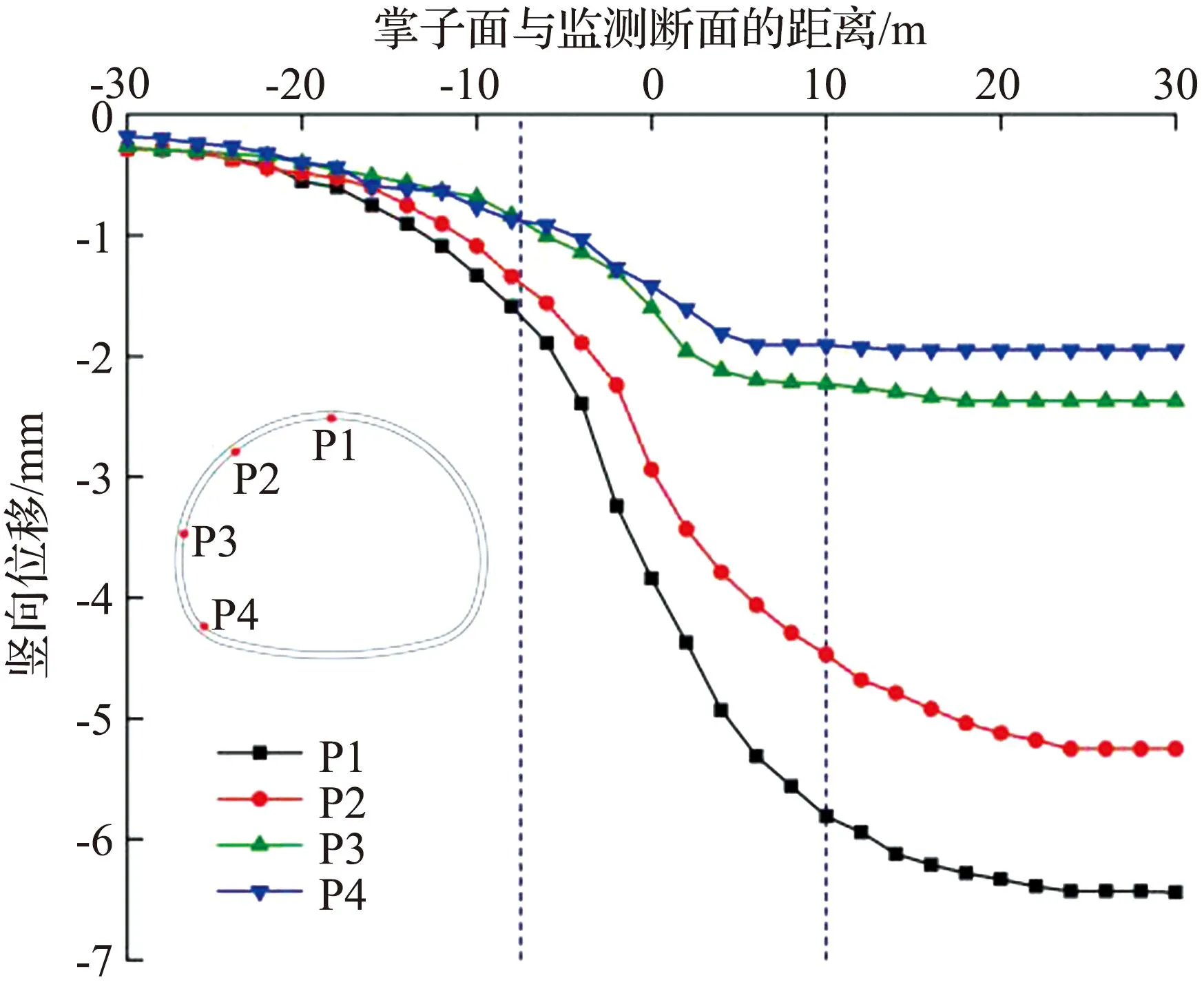
(a) 应力释放率λ=0.7

(b) 应力释放率λ=0.8图15 隧道开挖过程中的围岩位移Fig.15 Displacement of surrounding rock during excavation

为了更加准确地分析围岩的扰动程度和产生较大变形的范围,选取最危险位置的监测点数据对变形增量进行分析,隧道开挖过程中的围岩位移增量如图16所示。由图16可见,随着掌子面的推进,各监测点的变形增量不断增大,当掌子面越过监测断面后,变形增量逐渐减小至0。通过在位移增量为0.2 mm处作水平线,与围岩位移最大的拱顶和拱肩位置的变形增量曲线相交,此时对应的区域为变形增量急剧增大的范围,表明在进行初期支护时支护结构与掌子面间的距离不能超过这个范围,否则极易导致围岩易失稳。应力释放率为70%时,与拱顶的变形增量曲线相交时所对应的范围是(-7.5 m,10 m)。应力释放率为80%时,与拱顶的变形增量曲线相交时所对应的范围是(-10 m,10 m)。因此可以针对具体工程的实际情况适当选取合理的应力释放率。

(a) 应力释放率λ=0.7

(b) 应力释放率λ=0.8图16 隧道开挖过程中的围岩位移增量Fig.16 Displacement increment of surrounding rock during excavation

3.4 最佳支护时机确定方法

提取与开挖面距离L处的围岩变形值与距离开挖面足够远处同一位置的位移值进行对比,2个位置上位移的比值称为位移完成率[21]。引入位移完成率对围岩受开挖影响的程度进行准确分析,能够更加准确地表示初次支护对开挖岩体的变形控制能力。

r(L)=u(L)/u(∞)×100%,

(1)

式中:r代表开挖应力释放率,取值范围为[0,100%];u代表应力释放率为r时某点产生的位移。

根据围岩位移变化建立开挖应力释放率和掌子面距离监测断面的对应关系[22],即通过提取最危险位置产生的位移,计算得出该位置的位移完成率,以此作为横坐标,以掌子面与监测断面的距离L作为主纵坐标,以应力释放率λ作为次纵坐标,通过上述方法建立起位移完成率和应力释放率[23]的对应关系,基于位移完成率r的λ-L曲线如图17所示。根据已知的应力释放率可以求得掌子面与支护结构间的距离L。

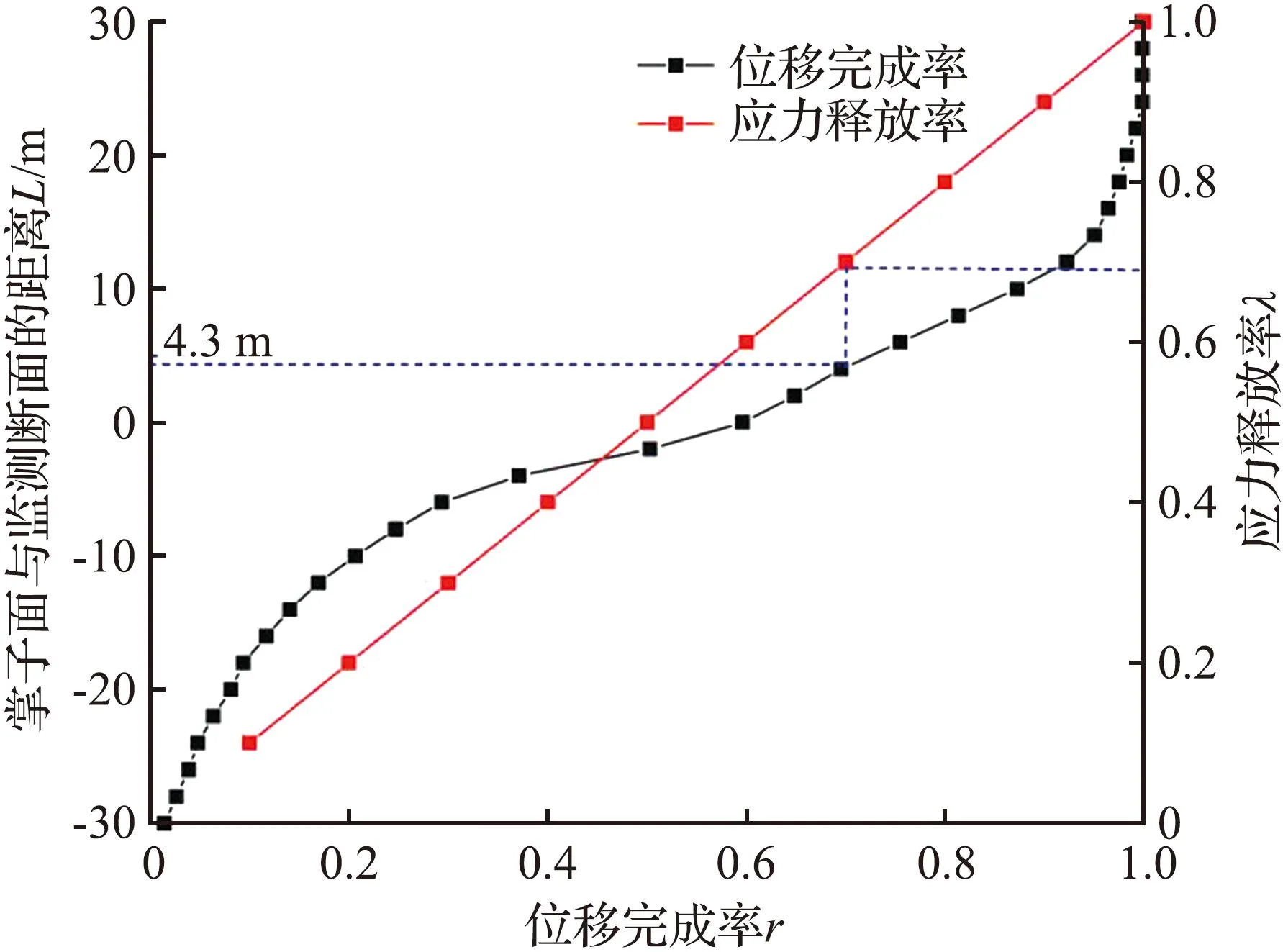
(a) 应力释放率λ=0.7

(b) 应力释放率λ=0.8图17 基于位移完成率r的λ-L曲线Fig.17 λ-L curves based on displacement completion rate r

以应力释放率70%为例进行分析。在右纵轴上找出应力释放率为70%的点作水平线与应力释放率曲线相交,然后在该交点上作竖直线找到此时位移完成率曲线上的交点,此时该点所对应的坐标即为掌子面与初期支护之间的控制距离,其值为4.3 m,在该安全距离内围岩应力得到充分释放并达到自稳状态。同理可得,当应力释放率为80%时,其初期支护距离不得超过7.6 m。因此济莱高铁宅科隧道初期支护施加最佳时机应控制在支护结构滞后于掌子面的距离为4.3～7.6 m。

4 结论

本文通过建立山区高铁隧道三维数值模型,研究了隧道开挖过程中围岩应力变化规律,分析了压力拱的形成机制及分布范围,得出了隧道纵截面压力拱形态特征图,在此基础上确定了隧道初期支护施作时机,得到以下结论:

① 通过对山区隧道开挖全过程中的围岩应力变化进行分析发现,在隧道开挖过程中,上部围岩中应力逐渐偏转,围岩荷载逐渐向四周传递,最终达到新的应力平衡状态,在隧道四周产生封闭环状应力表现为压力拱效应。

② 隧道仰拱靠近拱脚部位在0～24 m(即1.8D)的围岩参与成拱效应,围岩应力集中程度较高,承担着隧道拱部上方的围岩荷载,在施工过程中是逐渐扩展的,并且在仰拱下方能够形成稳定的压力拱。

③ 在进行隧道支护时机确定时,以应力释放率和掌子面与监测断面间的距离为变量,分析隧道开挖时围岩变化规律。随着隧道开挖应力释放率的不断增大,塑性区体积不断增大,并且在应力释放率达到90%时,出现塑性区体积率急剧增大的现象,因此认定在此之前增长较为缓慢的应力释放率即70%～80%是最佳初期支护时间点。

④ 为了更加直观地反映初期支护对于开挖面上方围岩变形的约束能力,引入位移完成率来衡量围岩受开挖扰动的程度,通过所建立的位移完成率和应力释放率的对应关系,获得实际最优支护时机。在本文所分析的实际工程中,通过对塑性区和位移完成率的分析,认为在隧道开挖时初期支护滞后于掌子面的距离应控制在4.3～7.6 m。