一种多运动模式的软体爬行机器人

张林贝子, 苏韩飞, 梁小流, 农卫航, 丁江,3*

(1.广西水利电力职业技术学院 交通工程学院, 广西 南宁 530023;2.广西大学 机械工程学院, 广西 南宁 530004;3.广西制造系统与先进制造技术重点实验室, 广西 南宁 530004)

0 引言

由柔性材料制成的软体机器人具有高度的柔性与灵活性,能较好地实现抓取[1-2]、滚动[3-4]和爬行[5-6]等基本功能,在越障、攀爬、抓取等机械化应用场景中展现了巨大的应用前景。其中,软体爬行机器人具有适应非结构化环境的优点,可以广泛应用于监测、救援和侦查等领域,引起了大量学者的关注[7-8]。

近年来,为了提升软体爬行机器人在地形方面的适应能力,学者们开发了多种不同运动模式的软体机器人。Wang等[9]设计了一种由智能复合材料制成的仿尺蠖软体爬行机器人,该机器人能够在水平面上实现直线运动和转弯运动。Umedachi等[10]研制了一种采用形状记忆合金为主要材料的软体机器人,该机器人通过改变自身的姿态和形状来调节与接触面间的摩擦力,不仅能够在水平面上爬行,而且对一定坡度的平面具有良好的适应能力。Yang等[11]将海星的微管足结构引入到机器人设计中,提出了一种可以在潮湿、凹凸不平的地面上爬行的软体机器人,使软体机器人对平面地形的适应能力得到了进一步加强。在执行任务过程中,仅能够在平面上爬行的软体机器人远不能适应复杂的地形,因此,研究者们开始开发能在管道或者杆状物之间爬行的软体机器人。Liao等[12]受到蛇缠绕运动的启发,研究了一种爬杆软体机器人,该软体机器人可以爬水平杆、垂直杆和弯曲杆等。Zhang等[13]设计了一种由硅胶材料制成的用于管道检测的软体爬行机器人,该软体机器人对弯曲和管径变化的管道都具有良好的适应性。

为了进一步拓展软体爬行机器人的多运动模式,本文中采用材质分别为聚乙烯和聚丙烯的2种商用波纹管为主体材料,通过浇注成型和3D打印技术,设计并制造了一种可以适应平面和杆地形的多运动模式软体爬行机器人,为提高软体爬行机器人地形适应性提供了一种新型结构。

1 软体爬行机器人的设计与制造

1.1 软体爬行机器人的设计

本文中设计的软体爬行机器人由1个转向伸缩执行器和2个弯曲执行器组成。转向伸缩执行器由3根弯曲性能良好的聚乙烯材质弹性波纹管组成,弯曲执行器采用伸缩性良好的聚丙烯材质波纹管。通过调节转向伸缩执行器的3根弹性波纹管内部压强,可控制其伸缩长度和转向角度。调节弯曲执行器的内部压强,可控制其弯曲半径。转向伸缩执行器与弯曲执行器之间采用热熔胶连接固定。

1.2 软体爬行机器人的制造

软体爬行机器人的制造过程如图1所示。弯曲执行器制造过程如图1(a)所示,弯曲执行器以聚丙烯材质波纹管(内径为14 mm,外径为20 mm,长度为50 mm)作为主体,在其侧面分别覆上限制层(热熔胶加热涂抹)、摩擦层、弹性层以及固定弹性层的橡胶圈,其中,将可折叠波纹管的每9个折叠单元作为一节,并采用橡胶圈将弹性层固定。弹性层的宽度为32 mm,厚度为0.2 mm;限制层的宽度为25 mm,厚度为1 mm;摩擦层的宽度为25 mm,厚度为5 mm。摩擦层由硅胶浇注成型得到,限制层与摩擦层之间采用硅胶专用胶粘接。转向伸缩执行器制造过程如图1(b)所示,转向伸缩执行器由3根弹性波纹管(内径为13 mm,外径为18 mm,长度为210 mm)与3D打印的刚性连接件组成,其中3根弹性波纹管的排布方式为沿同一圆周且间隔120°。软体机器人的整体装配效果图如图1(c)所示,2个弯曲执行器分别安装在转向伸缩执行器的两侧。

(a) 弯曲执行器制造过程

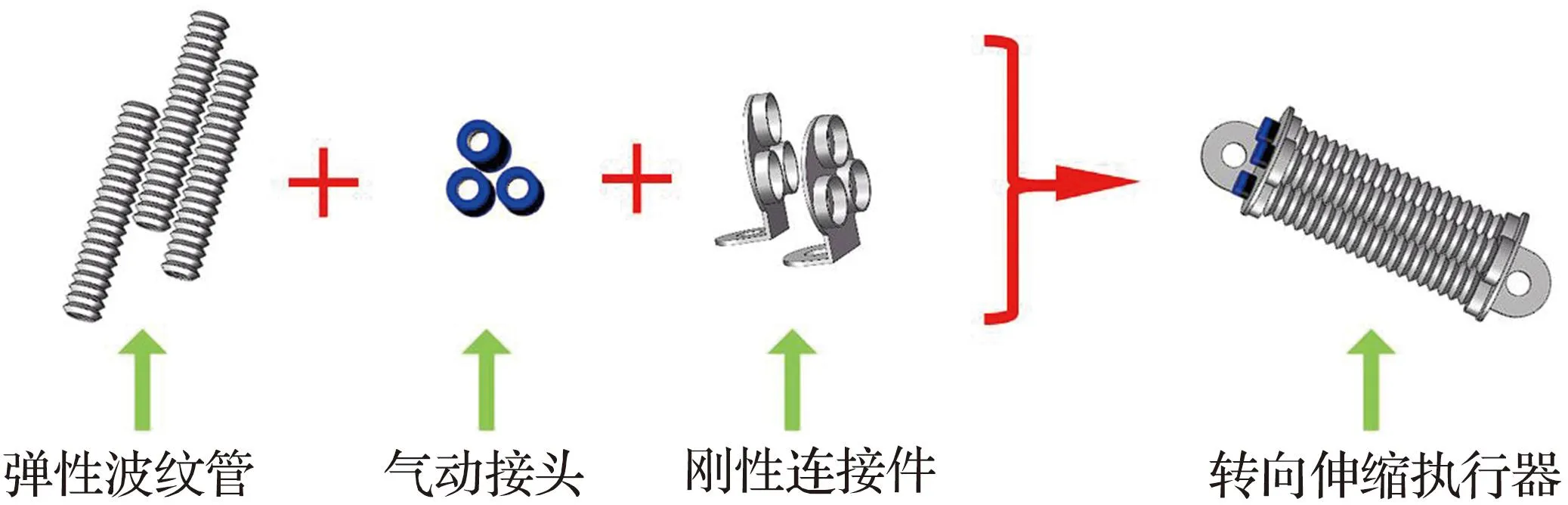
(b) 转向伸缩执行器制造过程

(c) 整体装配效果图1 软体爬行机器人的制造过程Fig.1 Manufacturing process of soft crawling robot

2 软体爬行机器人的运动模式

为了研究软体爬行机器人的运动步态控制规律,本文中将软体爬行机器人的运动步态规律划分为平面直行、平面转向和平面-杆过渡等3种模式。

2.1 平面直行模式

平面直行模式的运动步态如图2所示,分为6个运动步态:①左侧弯曲执行器充气弯曲,使摩擦层脱离地面,右侧弯曲执行器的摩擦层与地面接触,转向伸缩执行器处于放气状态;②转向伸缩执行器的3根弹性波纹管同时以相同负压吸气,由于右侧弯曲执行器与地面的摩擦力大于左侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动左侧弯曲执行器向右收缩移动;③左侧弯曲执行器放气,摩擦层与地面接触;④右侧弯曲执行器充气弯曲,使摩擦层脱离地面;⑤转向伸缩执行器的3根弹性波纹管同时放气,由于右侧弯曲执行器与地面的摩擦力小于左侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动右侧弯曲执行器向右伸长移动;⑥右侧弯曲执行器放气,摩擦层与地面接触。至此,该软体爬行机器人完成一个平面直行运动周期。

图2 平面直行模式的运动步态Fig.2 Motion gait diagram of straight plane mode

2.2 平面转向模式

平面转向模式的运动步态如图3所示,分为6个运动步态:①左侧弯曲执行器充气弯曲,使摩擦层脱离地面,右侧弯曲执行器的摩擦层与地面接触,转向伸缩执行器的3根弹性波纹管处于相同负压状态;②分别调节3根弹性波纹管的内部压强,使转向伸缩执行器弯曲成一定角度,由于左侧弯曲执行器与地面的摩擦力小于右侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动左侧弯曲执行器转向;③右侧弯曲执行器充气弯曲,使其摩擦层与地面脱离;④左侧弯曲执行器放气,使摩擦层与地面接触;⑤转向伸缩执行器的3根弹性波纹管同时以相同负压吸气,由于左侧弯曲执行器与地面的摩擦力大于右侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动右侧弯曲执行器转向;⑥右侧弯曲执行器放气,摩擦层与地面接触。至此,该软体爬行机器人完成一个平面转向运动周期。

图3 平面转向模式的运动步态Fig.3 Motion gait diagram of plane steering mode

2.3 平面-杆过渡模式

平面-杆过渡模式的运动步态如图4所示,分为10个运动步态:①左侧弯曲执行器一次充气弯曲成一定角度,并使摩擦层脱离地面,右侧弯曲执行器的摩擦层与地面接触,转向伸缩执行器的3根弹性波纹管处于相同负压状态;②转向伸缩执行器的3根弹性波纹管同时放气,由于左侧弯曲执行器与地面的摩擦力小于右侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动左侧弯曲执行器向左伸长移动,此时左侧弯曲执行器依靠其本身弯曲的高度运动到杆上;③左侧弯曲执行器二次充气弯曲,使其夹紧杆;④转向伸缩执行器的3根弹性波纹管同时以相同负压吸气,由于左侧弯曲执行器夹紧杆的力大于右侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动右侧弯曲执行器向左收缩移动;⑤左侧弯曲执行器一次放气,使其放松杆;⑥转向伸缩执行器的3根弹性波纹管同时放气,由于左侧弯曲执行器与杆的摩擦力小于右侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动左侧弯曲执行器向左沿杆伸长移动;⑦左侧弯曲执行器二次充气弯曲,使其夹紧杆;⑧右侧弯曲执行器一次充气弯曲成一定角度,并使摩擦层脱离地面;⑨转向伸缩执行器的3根弹性波纹管同时以相同负压吸气,由于左侧弯曲执行器与杆的夹紧力大于右侧弯曲执行器与地面的摩擦力,因此转向伸缩执行器带动右侧弯曲执行器向左沿杆收缩移动;⑩右侧弯曲执行器二次充气弯曲,使其夹紧杆。至此,该软体爬行机器人完成一个平面-杆过渡运动周期。

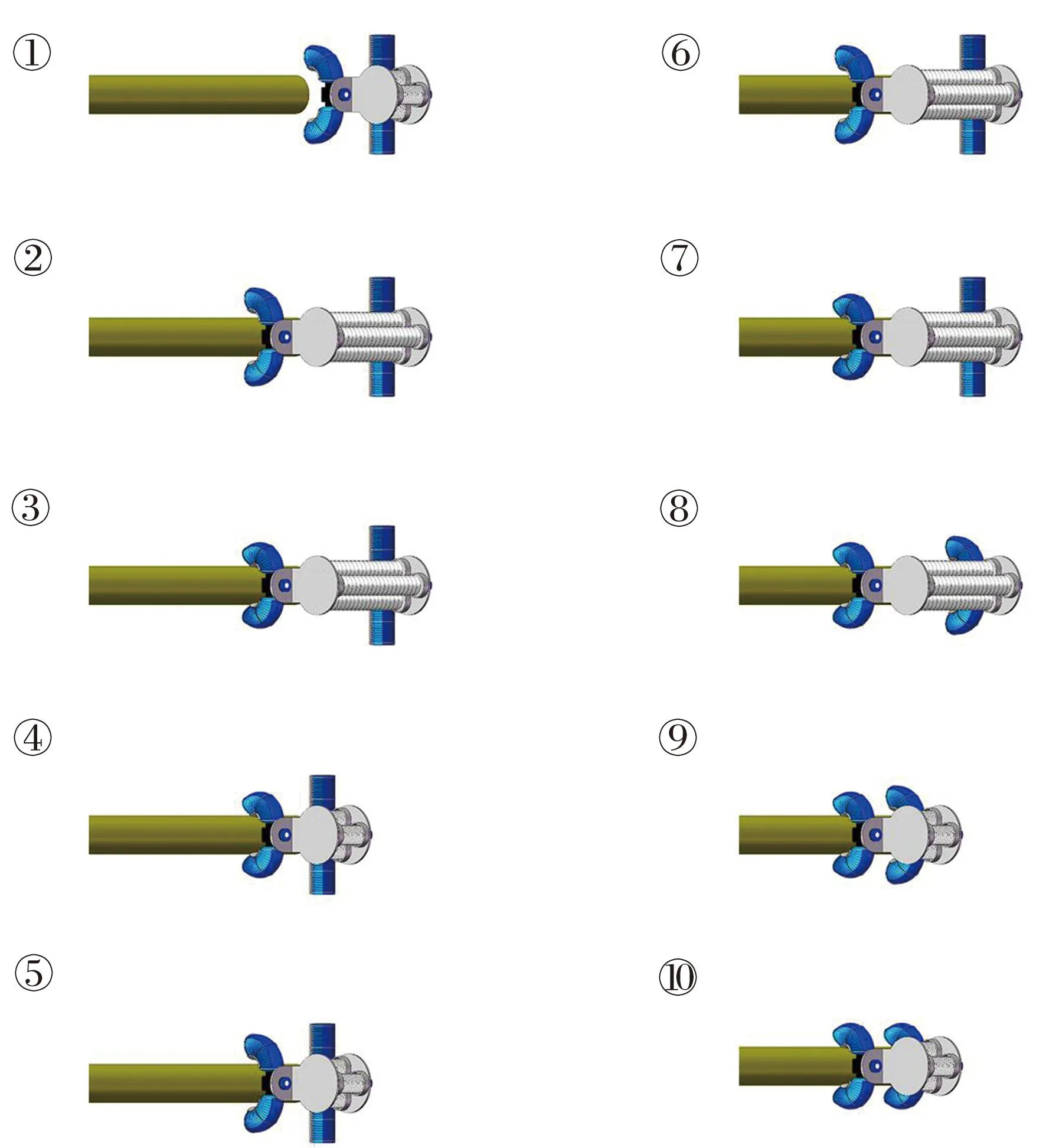
图4 平面-杆过渡模式的运动步态Fig.4 Motion gait diagram of face-rod transition mode

3 软体爬行机器人执行器的运动学模型

为了进一步得到压强与执行器弹性变形的定量关系,本文中基于常曲率假设,分析转向伸缩执行器伸缩和弯曲角度与压强的关系以及弯曲执行器弯曲半径与压强的关系,建立软体爬行机器人执行器的运动学模型。

3.1 转向伸缩执行器的运动学模型

转向伸缩执行器模型示意图如图5所示,其中伸缩模型、弯曲模型分别如图5(a)、图5(c)所示。

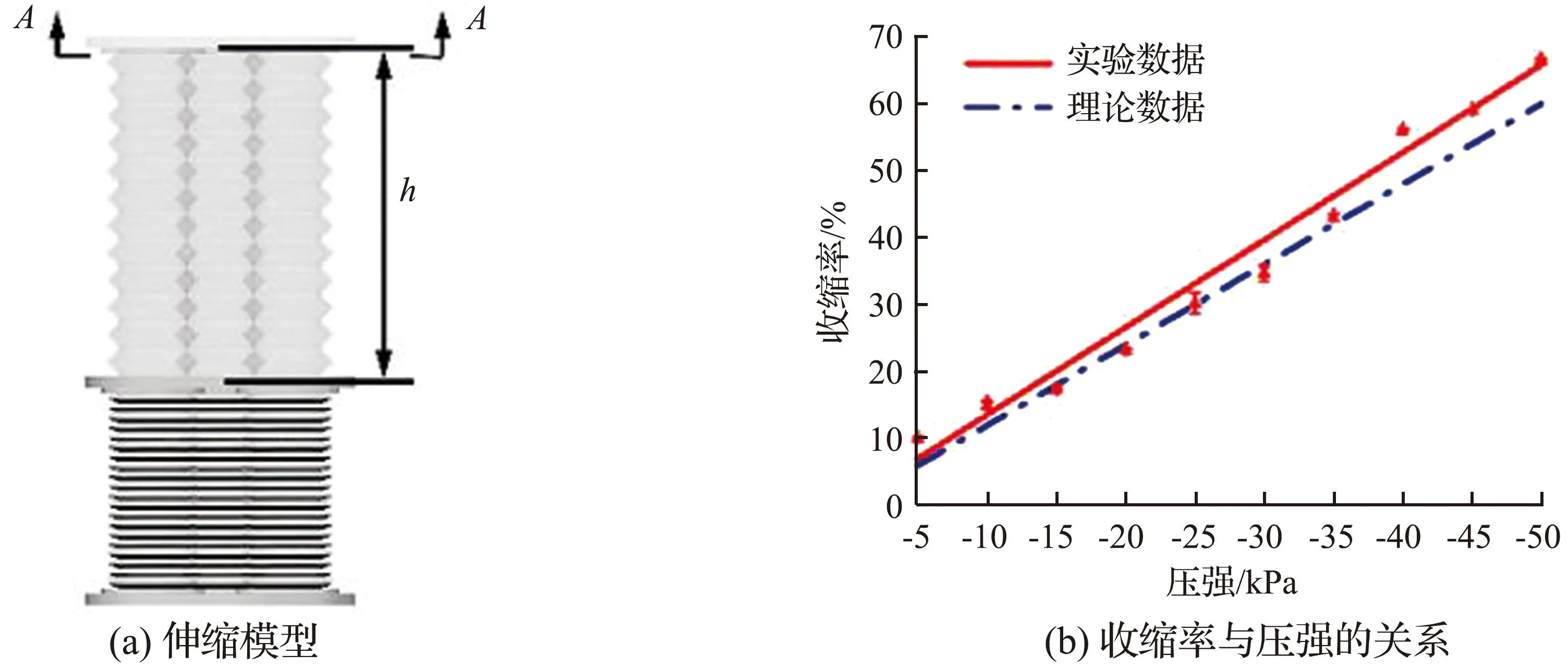
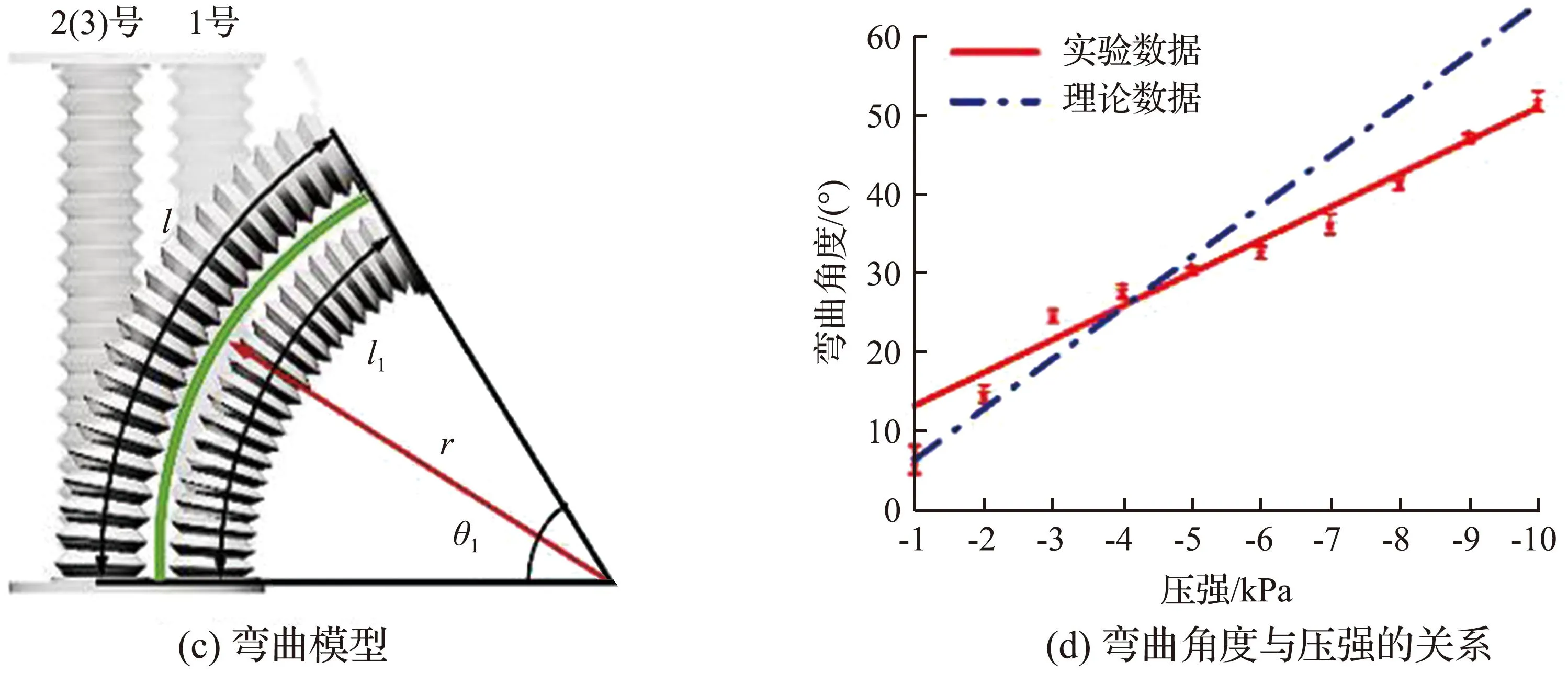
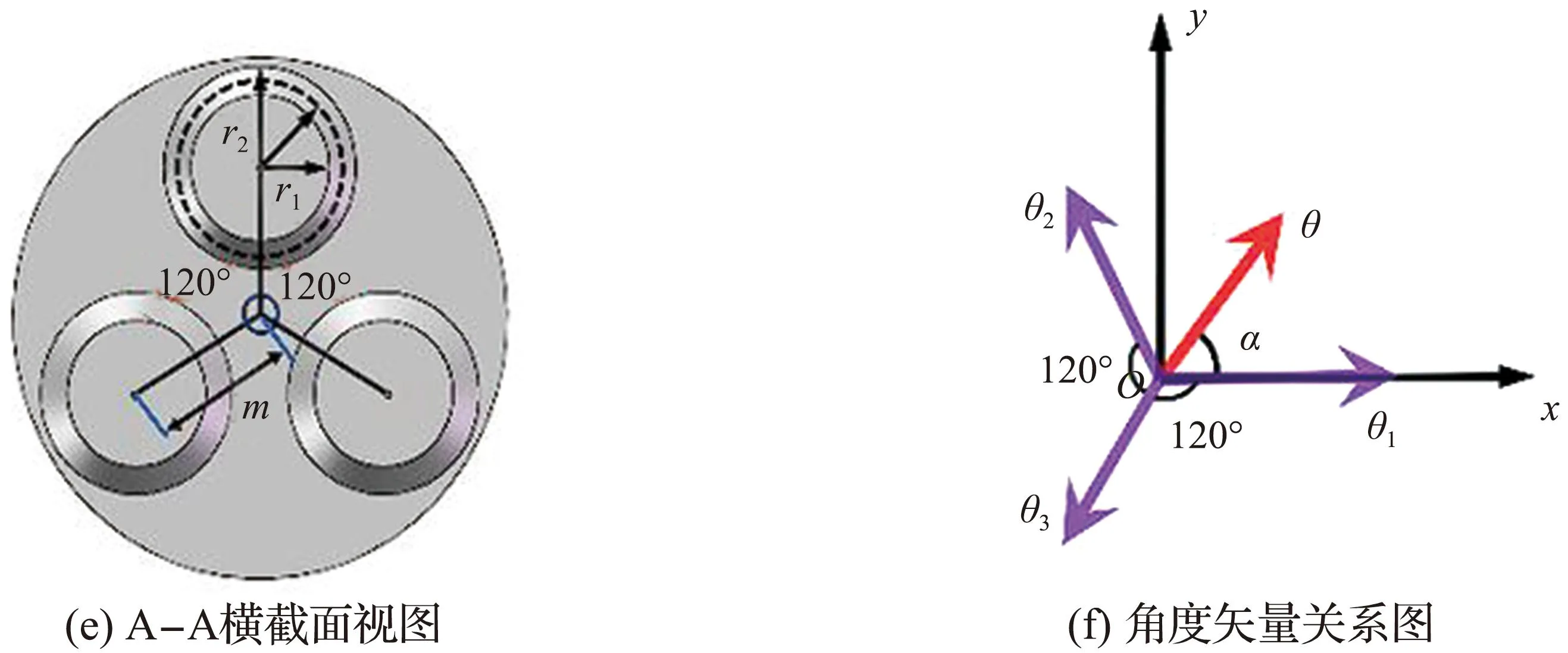
图5 转向伸缩执行器模型示意图Fig.5 Schematic diagram of steering telescopic actuator model

设F1为负压产生的收缩力,S1为弹性波纹管的横截面积。表达式分别为

F1=P1S1,

(1)

(2)

式中:P1为作用在弹性波纹管横截面上的压强;r1、r2分别为弹性波纹管横截面的内半径和外半径,将内半径与外半径和的1/2作为弹性波纹管横截面的实际半径。

转向伸缩执行器的弹性波纹管本身具有弹性,当压缩转向伸缩执行器时产生弹力,定义该弹力为F2, 设K1为单根弹性波纹管的弹性系数(K1=0.074),h为转向伸缩执行器的收缩量,则有

F2=K1h。

(3)

联立式(1)—(3),得到转向伸缩执行器的收缩量与压强的关系式(4)。图5(b)为收缩量与压强关系的理论和试验曲线。

(4)

由于弹性波纹管的变形是非均匀的,因此基于常曲率假设,假设3根弹性波纹管的每个微单元都是常曲率变形,以便于理论分析。

(5)

式中:l为弹性波纹管在标准大气压下的长度;θ1表示当且仅对1号弹性波纹管吸气时转向伸缩执行器的弯曲角度;m为转向伸缩执行器端盖处弹性波纹管圆心与端盖中心之间的距离。l1表示当且仅对1号弹性波纹管吸气时,1号弹性波纹管的长度,且

l1=θ1(r-m)。

(6)

联立式(5)、(6),得到当且仅对1号弹性波纹管吸气时,转向伸缩执行器的弯曲角度与1号弹性波纹管长度的关系式为

(7)

同理,当且仅对2号弹性波纹管、3号弹性波纹管吸气时,得到

(8)

(9)

式中:θ2为当且仅对2号弹性波纹管吸气时转向伸缩执行器的弯曲角度;θ3为当且仅对3号弹性波纹管吸气时转向伸缩执行器的弯曲角度;l2表示当且仅对2号弹性波纹管吸气时,2号弹性波纹管的长度;l3表示当且仅对3号弹性波纹管吸气时,3号弹性波纹管的长度。由图5(f)角度矢量关系,可得到关系式(10)—(12)。

θx=θ1-θ3sin30°-θ2sin30°,

(10)

θy=θ2cos30°-θ3cos30°,

(11)

(12)

式中:θ为转向伸缩执行器整体弯曲角度;θx为转向伸缩执行器x方向上的角度;θy为转向伸缩执行器y方向上的角度。

联立式(7)—(12),得到转向伸缩执行器弯曲角度与3根弹性波纹管长度的关系式(13)。

(13)

定义转向伸缩执行器的转向角度α,由图5(f)中的几何关系可以得到式(14)、(15)。

(14)

(15)

联立式(10)、(11),得到转向伸缩执行器转向角度与3根弹性波纹管长度的关系式(16)。

(16)

根据α的正负以及cosα的大小可以确定转向伸缩执行器绕x轴正向逆时针转过的角度。

联立式(4)、(7),得到当且仅对1号弹性波纹管吸气时,转向伸缩执行器弯曲角度与压强的理论关系式(17)。同时,通过试验可得到转向伸缩执行器单根弹性波纹管吸气时,压强与弯曲角度的关系曲线[图5(d)]。

(17)

3.2 弯曲执行器的运动学模型

弯曲执行器模型示意图如图6所示,其中弯曲模型如图6(a)所示。在弯曲执行器的弹性变形范围内,其弹性力与膨胀力相等,得到下面的关系式:

(a) 弯曲模型

(b) 弯曲半径与压强的关系图6 弯曲执行器模型示意图Fig.6 Schematic diagram of bending actuator model

F3=K2(L2-L1),

(18)

(19)

F3=F4,

(20)

式中:F3为弯曲执行器弹性变形时产生的弹性力;F4为充气产生的膨胀力;K2为弹性系数(K2=0.452 N/mm);R1、R2分别为波纹管的内半径与外半径;P2为弯曲执行器的内部压强;L1为弯曲执行器弹性层变形前的长度;L2为弯曲执行器变形后的外弧长。

为了研究弯曲执行器的弯曲半径与压强的关系,可通过图6(a)中的几何关系得到式(21)—(23),并联立式(18)—(20),得到弯曲执行器的弯曲半径与压强的关系式(24)。

L1=L3,

(21)

L3=βR,

(22)

L2=β(R+2R2+δ1+δ2+δ3),

(23)

(24)

式中:L3为内弧长,长度与L1相等(L1=18 mm);R为弯曲半径;β为弯曲角度;δ1为弹性层厚度(δ1=0.2 mm);δ2为限制层厚度(δ2=1 mm);δ3为摩擦层厚度(δ3=5 mm)。由于δ1较小,因此在计算时忽略弯曲执行器弯曲时导致弹性层的厚度变化。根据式(24)绘制了弯曲执行器弯曲半径与压强的理论关系曲线,并通过试验绘制出实际关系曲线与之对比[图6(b)]。

4 试验与结果讨论

本文中对该软体爬行机器人的3种运动模式进行了试验验证。平面直行运动如图7所示。在试验中,通过同时对转向伸缩执行器的3根弹性波纹管吸气与放气,实现转向伸缩执行器的伸缩,对弯曲执行器充气与放气,改变软体爬行机器人与地面的摩擦力,以此实现软体爬行机器人的平面直行。平面直行试验结果与设计的直行运动基本一致。

图7 平面直行运动Fig.7 A straight line motion graph

平面转向运动如图8所示。调节该软体爬行机器人转向伸缩执行器3根弹性波纹管的压强,使摩擦层脱离地面的左侧弯曲执行器转过一定角度,右侧弯曲执行器充气,使其摩擦层也脱离地面,左侧弯曲执行器放气使其摩擦层与地面接触,由于左侧弯曲执行器与地面的摩擦力较大,因此将转向伸缩执行器放气,右侧弯曲执行器会随左侧弯曲执行器的转向角度进行转向。

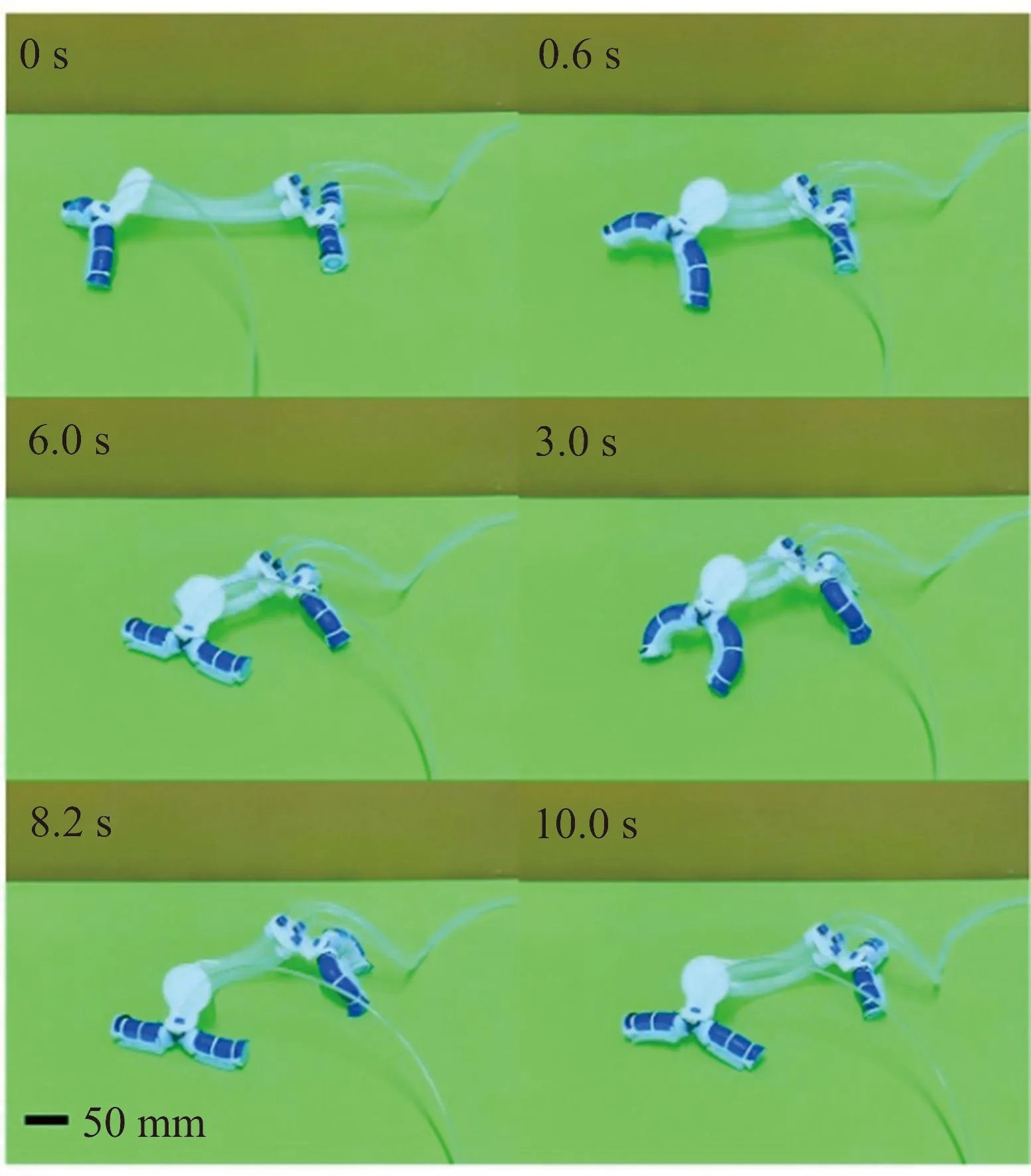
图8 平面转向运动Fig.8 Plane steering motion diagram

平面-杆过渡运动如图9所示。通过对弯曲执行器充气使其摩擦层脱离地面并弯曲成一定高度,以此来改变其与地面的摩擦力并穿过杆,通过对弯曲执行器的二次充气使其夹紧杆,依靠弯曲执行器对杆的夹紧力使软体爬行机器人固定在杆上,同时借助转向伸缩执行器的伸缩实现软体爬行机器人前行。在试验中,软体爬行机器人的弯曲执行器通过调整弯曲高度与角度来适应杆的直径,并成功地实现了平面-杆过渡运动。

图9 平面-杆过渡运动Fig.9 Face-bar motion diagram

5 结论

本文提出了一种多运动模式软体爬行机器人,并以波纹管为主体材料制作了软体爬行机器人样机。将软体爬行机器人的运动模式划分为平面直行、平面转向和平面-杆过渡3种,并建立软体爬行机器人执行器的运动学模型以分析其弹性变形与压强的关系。通过试验验证了执行器运动学模型的正确性,证明了软体爬行机器人3种运动模式的可行性。