基于动态神经网络NARX时间序列的双排桩基坑变形预测

侯福昌, 曾家俊, 江杰, 李结全, 范懿文

(1.广西瑞宇建筑科技有限公司, 广西 南宁 530004;2.桂林理工大学 土木与建筑工程学院, 广西 桂林 541004;3.广西大学 土木建筑工程学院, 广西 南宁 530004;4.工程防灾与结构安全教育部重点实验室, 广西 南宁 530004;5.广西建设职业技术学院 土木工程学院, 广西 南宁 530004)

0 引言

随着我国基础建设的发展,工程建设在许多地区如火如荼地进行着。近年来,双排桩支护结构以抗弯刚度大、场地占用小及施工方便快捷等优势,在城市基坑施工中大量使用。基坑工程是一个多学科交叉、施工动态变化、多因素影响、施工技术复杂的系统工程,同时土体存在明显的地域性、时空性、弹塑性以及不均匀性等特点,如何实现科学有效、动态预测和预见性掌握基坑的变形规律是本文探讨的重点。

近年来,岩土体的变形预测成为世界研究热点,并有国内外学者取得了丰富的研究成果。张冬晓[1]采用灰色系统理论通过采集的监测数据建立了基坑变形GM(1,1)模型,并将其成果应用于基坑动态设计,指导信息化施工。刘俊城等[2]基于长短期记忆神经网络(long short-term memory, LSTM)智能算法理论构建了LSTM多步预测模型,并对模型输入集空间维度和时间维度2个超参数进行探究,提高了模型的预测准确度。赵燕容等[3]通过利用润扬长江公路大桥南汊悬索桥南锚碇基坑随时间变化的监测数据,采用小波理论建立了基于时间序列的基坑动态预测模型。孙世国等[4]分别采用时间序列模型自回归滑动平均序列模型(auto regressive moving average sequence model, ARMA)法和灰色系统理论GM(1,1)模型依托某矿边坡变形监测数据,进行了单项预测模型和组合预测模型的研究,发现后者预测精度更高更可靠。杨帆等[5]依托三峡库区宽河谷段的白水河滑坡监测项目,开展了人工蜂群-时间序列模型结合支持向量回归机(support vector regression, SVR)的预测模型研究,并取得了较好的预测效果。鲍燕妮等[6]依托新田长江大桥锚碇基坑地表和危岩裂缝变形监测数据,采用时间序列ARMA模型对基坑地表沉降值和危岩裂缝变形值进行预测,并取得了较好的精度。宋楚平[7]采用遗传算法结合BP神经网络解决基坑变形的非线性和不确定性问题,并应用于南通市一号线某站点的基坑变形预测,取得了较好的预测效果。

由于土体具有复杂的物理力学特性,并且基坑变形影响因素(如开挖速率、施工水平以及现场人工活动等)繁杂,因此利用传统的土力学理论无法实现土体变形的高精度预测[8-10]。目前对于双排桩支护机制的研究尚未取得突破,现场监测、室内试验及数值模拟等工作仍有较多的待完善之处[11]。目前大多数的基坑变形和边坡稳定性的研究主要是基于传统土力学理论对支护结构或周边邻近建筑物的变形规律的研究,而基坑变形是一种随时间明显变化的特征,因此基于时间序列数据的分析预测模型为基坑变形演变研究提供了一种方法和途径。此外,采用双排桩基坑支护形式的基坑工程通常紧邻建筑物,四周遍布重要管线,且基坑支护结构在产生较大变形后通过基坑监测数据才能得出具体变形情况,很可能因预警不及时造成基坑失稳,产生严重后果。针对于此,本文在已有研究基础上,依托南宁市亭洪路72号河南水厂住宅小区危旧房改造项目双排桩基坑,基于带有外部输入的非线性自回归(nonlinear-auto-regressive model with exogenous inputs, NARX)神经网络建立时间序列预测模型,对基坑双排桩支护结构的变形发展进行预测预报,并将预测结果与实际结果进行对比分析,研究成果可以为相关工程建设提供一定的技术参考。

1 动态神经网络NARX时间序列模型

1.1 原理概述

时间序列是指在生产生活中通过观察记录某一现象的时间变化过程,并形成观察值随时间先后顺序的变化而变化的数列,包含了某个变量或多个变量在不同时间点上的随机数据,反映了现象的发展变化规律[12]。时间序列分析法[13]认为观测所得到的数据值之间存在一种相互关联的联系,此种联系影响着系统的发展趋势和动态变化,可以通过数据间的这种自相关关系来进行时间序列预测,从而获得未来的发展趋势。常见的时间序列模型主要有自回归时间序列模型(auto regressive time series model,AR)、移动平均时间序列模型(moving average time series model,MA)和ARMA。

人工神经网络是一种模仿动物神经网络行为特征,进行分布式信息处理的数学模型算法,其将输入数据投射到设置的若干个非线性映射层即隐含层上,通过数据训练以获得输入数据和输出数据之间的数学关系[14-16]。人工神经网络具有自学习功能、联想存储功能和高速寻找最优解的能力,常见的神经网络模型主要包括输入层、隐含层和输出层,层与层之间通过网络和节点连接并配以权重进行运算,从而获得最优解[17]。

常规时间序列模型数据假设是线性的、平稳的且是参数化的,其优点是具有较强的处理随机项和线性数据处理能力,对于存在趋势项、非平稳、非线性的数据处理效果较差。相比之下,神经网络具有强大的自学习、自适应的优势,具有强大的非线性映射处理能力,能够处理复杂的非线性问题。因双排桩基坑变形影响因素众多,且呈现非线性、非平稳的特点,为了提高模型的预测精度和准确性,本文提出采用动态神经网络NARX模型建立时间序列预测模型,以解决双排桩基坑变形监测中的多因素、非线性、模糊性等问题。

1.2 神经网络结构

传统神经网络模型结构如图1所示,一般分为输入层、隐含层和输出层。首先通过输入层将输入数据和初始权重相乘并求和,然后经偏执项修正后,再代入隐含层的函数进行计算,随后把计算结果作为新的输入经隐含层与输出层设置的函数计算输出。输出后观察输出计算值和真实值之间的差值,并将误差返回各个神经元节点,再重复修正各层之间的权值,直至达到容许误差。

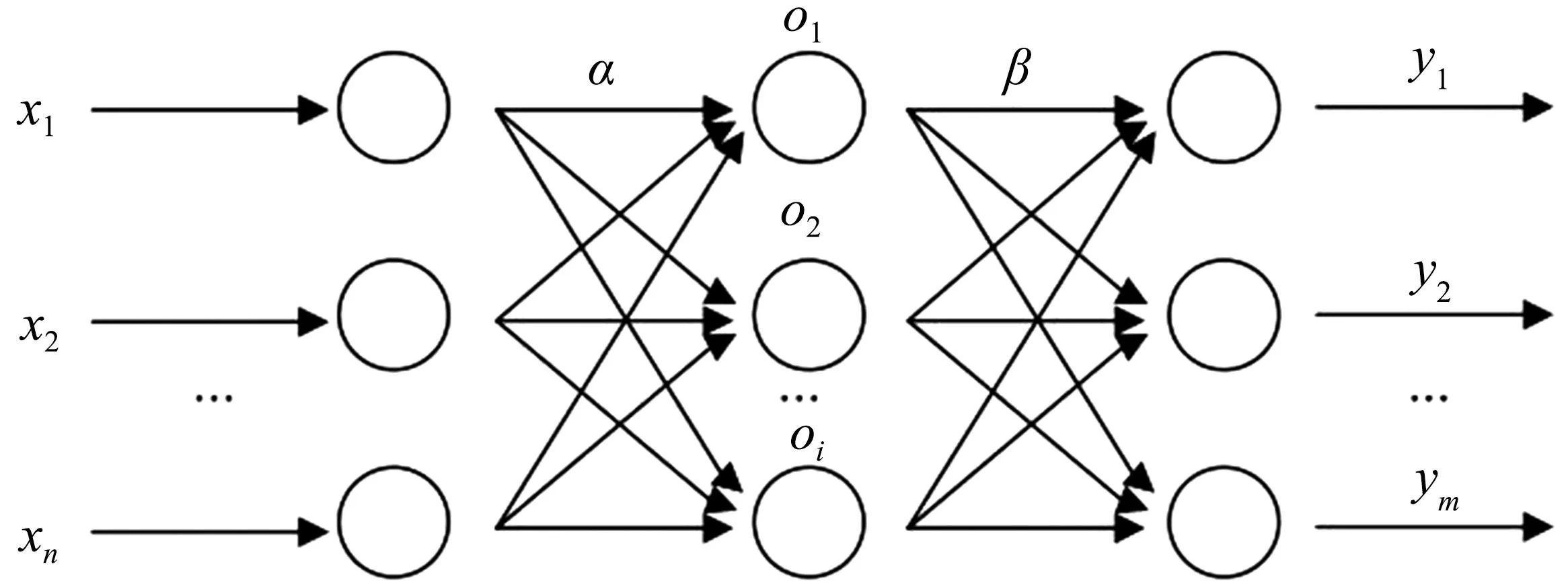
图1 传统神经网络模型结构Fig.1 Traditional neural network model structure

在神经网络模型的基础上增加研究对象的时间序列参数,即为神经网络时间序列模型。将研究对象时间序列现在与之前的误差项和之前值构建非线性函数[18],并将其输入到神经网络中。设神经网络时间序列输入为x= (x1,x2, …,xn)T,则输入层节点到隐含层节点以及隐含层节点到输出层节点之间的关系可以表示为

(1)

(2)

输出结果为

(3)

(4)

均方差为

(5)

式中:αkn为输入层与隐含层间的连接系数;βmk为隐含层与输出层间的连接系数;μk和λm分别为αkn、βmk的阈值,k为隐含层神经元个数;M为样本数量;bm为样本数据标准值;n为输入向量长度;m为输出向量长度。

动态神经网络NARX模型结构如图2所示。

图2 动态神经网络NARX模型结构Fig.2 NARX neural network time series model structure diagram

由图2可见,NARX神经网络通过加入延时和反馈机制增强了神经网络对历史数据的记忆能力,形成了一种新的动态神经网络。NARX动态神经网络模型可用于解决非线性离散问题,可综合表示为

y(t)=f{u(t-Du),…,u(t-1),u(t),y(t-Dy),…,y(t-1)},

(6)

式中:u(t)为网络在t时刻的输入;y(t)为网络在t时刻的输出;Du为网络输入时延的最大阶数;Dy为网络输出时延的最大阶数;u(t-Du),…,u(t-1)为网络相对于t时刻的前期输入;y(t-Dy),…,y(t-1)为网络相对于t时刻的前期输出。

1.3 基坑变形预测模型的工作流程

基于神经网络的基坑变形量预测时间序列模型如图3所示。由图3可见,基于神经网络的预测模型可分为数据端、训练端和计算端3个部分。在数据端,对监测到的基坑变形量数据预处理并进行分析,确定引起基坑变形的重要参数,引入时间序列,然后将数据分为两大模块,分别对其进行训练和计算。在神经网络训练端,运用构建出的动态神经网络NARX结构对其进行测试。最后,导入通过神经网络训练得到的数据,对模型进行验证,并得到最优解,实现多步预测。

图3 基于神经网络的预测模型Fig.3 Prediction model based on neural network

2 工程概况

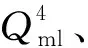
本工程自2022年3月17日开始分2个阶段开挖施工,第1阶段施工2#楼,第2阶段施工1#楼,历时5个多月,共监测62次。监测点类型包括坡顶水平和竖向位移(ZDS)、深层水平位移监测(CX)、周边地表竖向位移监测(D)、地下水位监测(SW)、道路沉降(DL)、管线沉降(GX)、建筑沉降(JC)、锚索轴力监测(ZL)。

3 预测模型的实现

对双排桩而言,影响基坑变形的因素有双排桩尺寸及土体参数[19-20]、桩间土的挤出效应[21]、桩-土接触关系[22]、空间效应[23]、圈梁连梁间的协同作用[24]、开挖方法及深度、土体暴露时间等。在这些因素中除开挖方法及深度和土体暴露时间外,其他因素均为基坑支护体系的固有特性,不随时间的变化而变化,因此,本文中建立时间序列模型时考虑了开挖深度和土体暴露时间2种因素随时间变化对基坑变形的影响。

除此之外,结合基坑的整个监测过程,根据工程监测数据资料和施工组织设计,并且考量基坑失稳对周边环境的影响程度,选取道路沉降位移DL1、坡顶水平和竖向位移ZDS1前57次监测数据建立模型,用最后5次监测所获数据作为多步预测的对比数据进行分析。

建模时采用MATLAB软件分别建立DL1和ZDS1动态神经网络NARX时间序列网络模型,对于常见的训练算法而言,考虑到Levenberg-Marquardt(LM)算法收敛时间短且训练精度高,而量化共轭梯度(scaled conjugate gradient, SCG)算法适用于求解线性方程,贝叶斯正则化(bayesian regularization, BR)算法占据较大内存且收敛时间过长,本文训练算法选取LM算法,模型参数隐含层数为10,时滞数为2。建立的NARX模型神经网络时序结构由输入层、隐含层和输出层3个部分组成,神经网络NARX时序网络结构如图4所示。

(a) DL1

(b) ZDS1图4 神经网络NARX时序网络结构Fig.4 NARX neural network time series network structure

神经网络时序模型的开发训练结果分别如图5、图6所示。从图5、图6中可以看出,模型训练效果较理想,目标值与输出值整体保持一致,若增大数据量,能使模型进行深度学习,进一步提高训练精度。在DL1时序模型中期望值与输出值匹配较好,几乎没有误差。而ZDS1模型与之相比,整体存在一定误差,说明DL1的精度较高。对于不同类型的数据,选择合适的算法能使预测模型高效训练,同时测试数据的离散性也会降低模型预测的准确度。

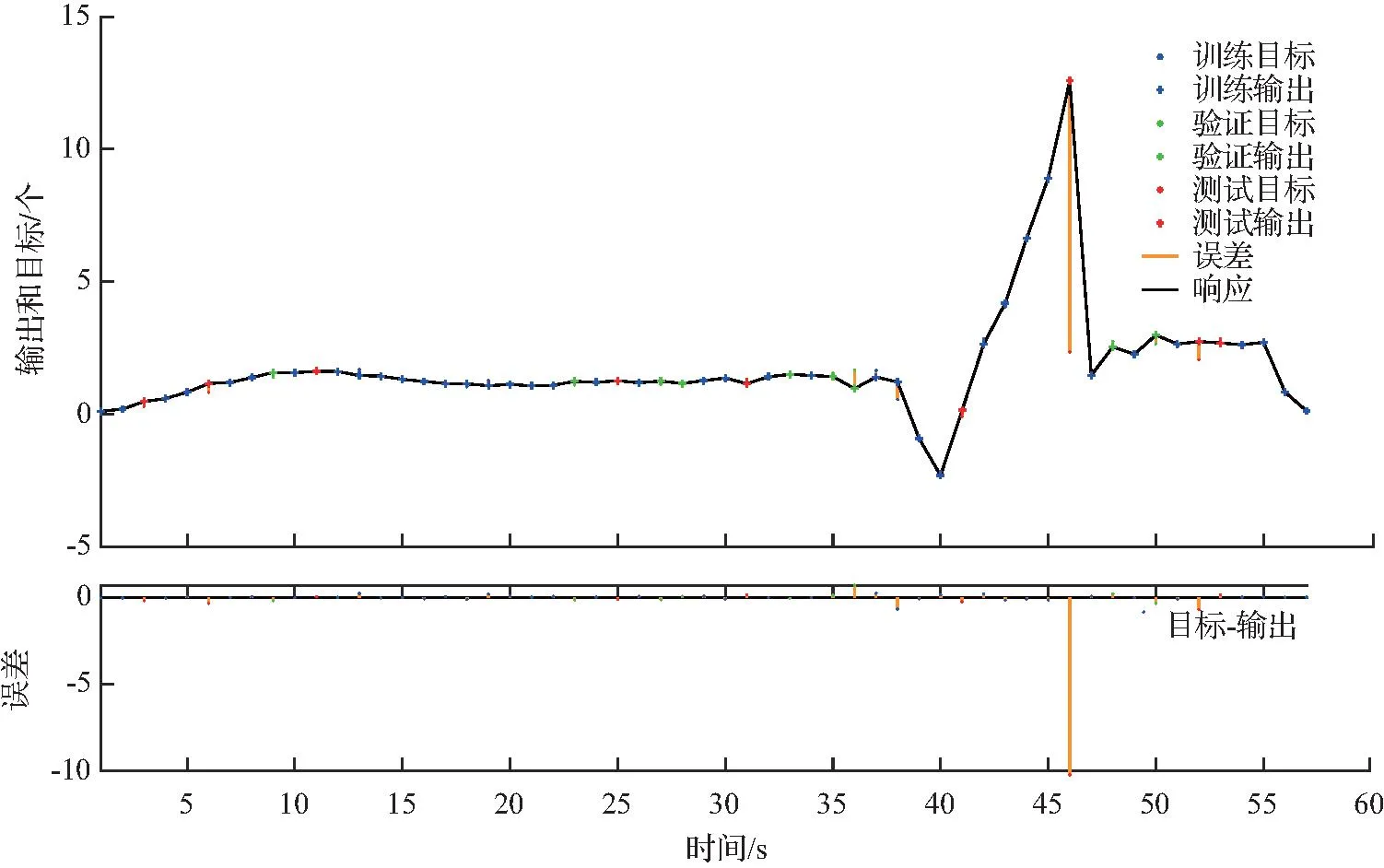
图5 DL1时序模型训练响应Fig.5 Training response of DL1 time series model

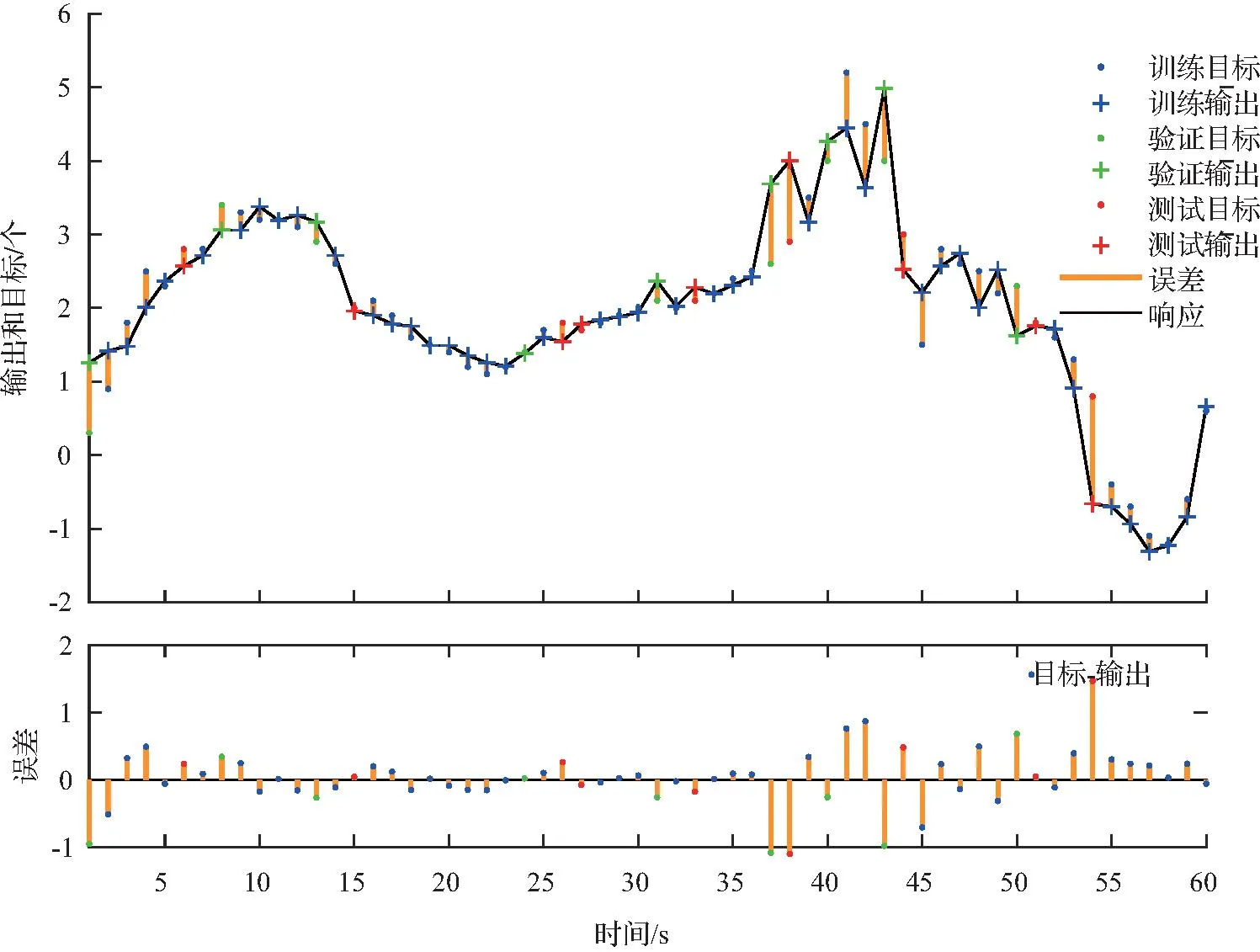
图6 ZDS1时序模型训练响应Fig.6 Training response of ZDS1 time series model

对于NARX时间序列模型,模型预测时只有考虑除随机因素(如噪声等)外的所有影响因素,才能达到理想训练,可以通过观察误差自相关图来检验训练效果。时序模型误差自相关性如图7所示。误差自相关性是指训练误差与时间延迟之间的关系,图7中零点处的竖线为零相关线,表示误差自身的相关性,其余延迟点上的输入数据误差自相关性应为0。事实上,理想的训练结果是不可能的,因此,本文设定了95%的置信限,认为输入误差自相关性在该区间内是能接受的,训练结果理想。从图7中可以看出,ZDS1、DL1模型的训练结果均相对理想,除零相关线外,其余位置的自相关性在置信区间内。

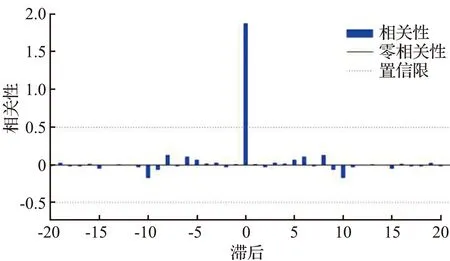
(a) DL1模型

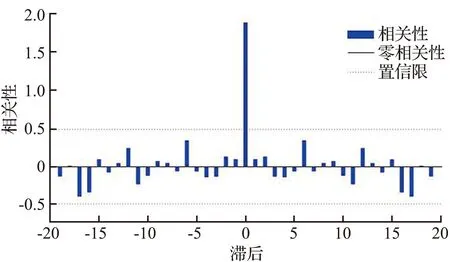
(b) ZDS1模型图7 时序模型误差自相关性Fig.7 Error autocorrelation of time series model

动态神经网络时序模型误差直方图如图8所示。

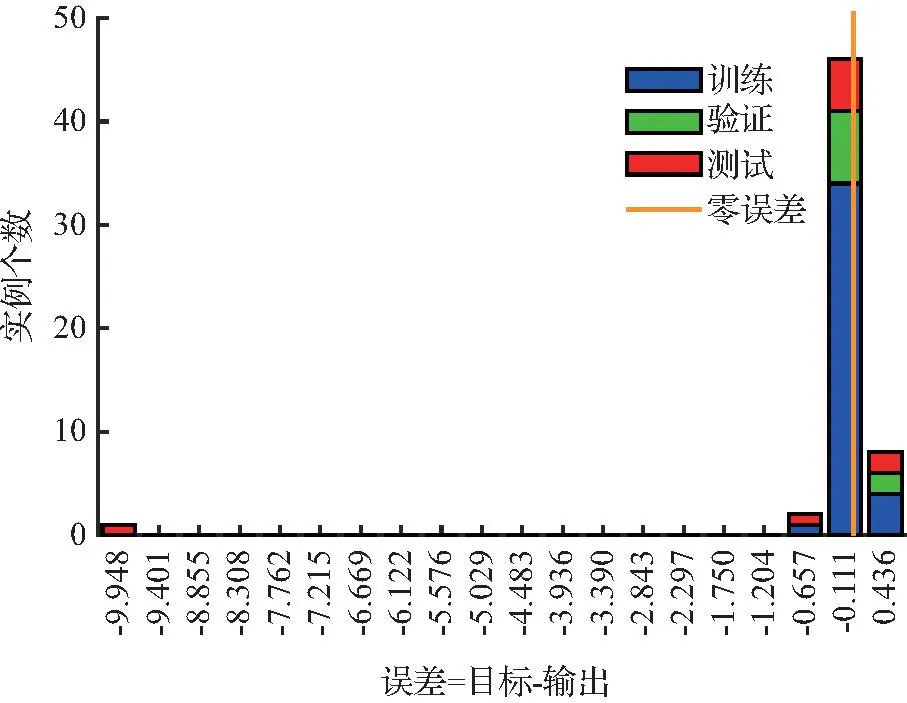
(a) DL1模型

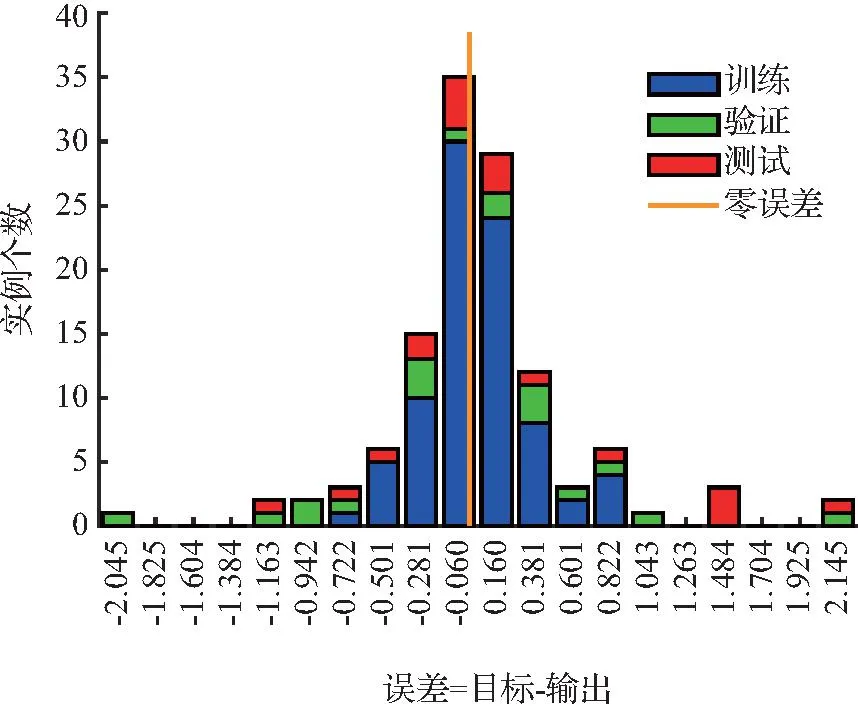
(b) ZDS1模型图8 动态神经网络时序模型误差直方图Fig.8 Dynamic neural network time series model error histogram

从图8中可见,横坐标表示基坑变形位移值相对误差,其值为真实值(目标值)与预测值(输出值)差值,纵坐标为测试实例数。变形值误差集中在零误差线附近。对于DL1模型,实例处于-0.1 ～ 0.4的数量最多,其中误差处于-0.1～0的实例数量最突出,随着相对误差绝对值的增大,实例数量逐渐减少,所有相对误差的值处于-10.0～0.5,集中在零误差线左侧。而对于ZDS1模型,实例数量较多的区间介于-0.3 ～ 0.4,所有误差值介于-2.0～ 2.0,实例数量在零误差线两侧的分布较均匀,越靠近零线的位置点实例数量越多,满足预测要求。由此可见,ZDS1模型能够精确地预测基坑坡顶的位移,而DL1模型需进行改进并重新选取算法以训练,完成预期的预测。

4 可行性分析

表1、表2分别是根据基坑整个监测阶段最后5次(2022年7月27日至8月24日)的实际监测数据得到的DL1、ZDS1预测值。所有预测值与实际监测值在相同方向上的变化趋势保持一致,当实际监测值增大时,模型预测值也随之增大,然而,基坑监测采样间隔(间隔为7 d)在一定程度上降低了预测模型的准确性。采样间隙过程中的不可抗力因素导致模型所依赖的有效历史数据有所减少,但是模型从整体上准确地预测了基坑变形的演变规律,能够满足大部分实际工程需要。下一步可以考虑缩短采样间隔,以优化模型预测精度。

表1 DL1模型竖向位移预测值与实际监测值Tab.1 DL1 model vertical displacement forecast values and the actual monitoring values 单位:mm

表2 ZDS1模型水平位移预测值与实际监测值

DL1模型竖向位移预测值与实际值对比、ZDS1模型水平位移预测值与实际值对比分别如图9、图10所示。

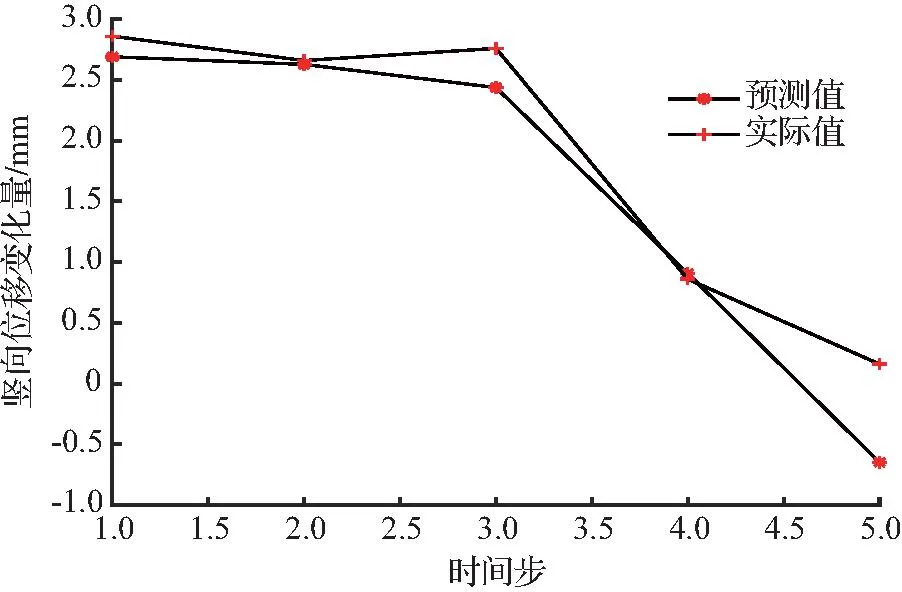
图9 DL1模型竖向位移预测值与实际值对比Fig.9 Comparison of predicted values and actual values of vertical displacement of DL1 model

(a) y方向

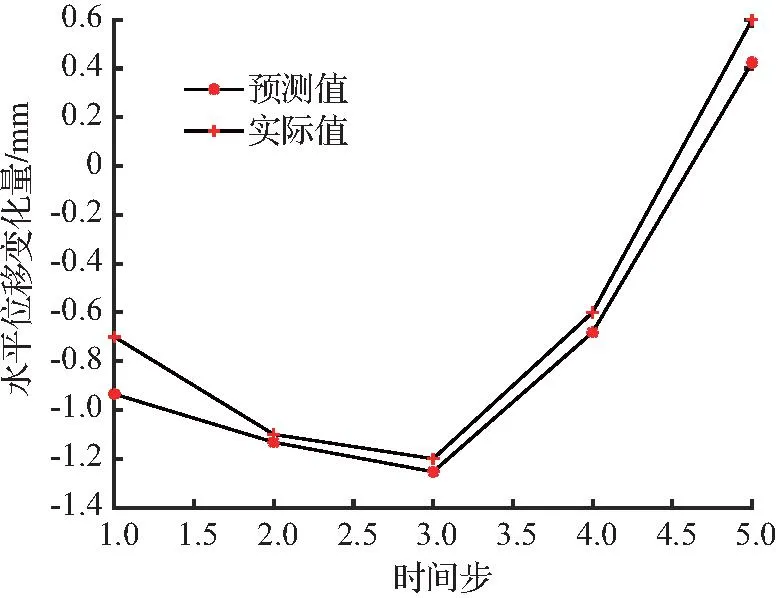
(b) x方向图10 ZDS1模型水平位移预测值与实际值对比Fig.10 Comparison of predicted values and actual values of horizontal displacement of ZDS1 model

通过对比可以发现,个别监测点的预测值存在偏差,使模型预测效果受到影响,这种偏差并非是神经网络结构自身缺陷引起的,而是由基坑情况的复杂性、不确定性所导致的,因此需进一步考虑各种潜在的影响因素,以减少偏差。除此之外,采样时间间隔的设定也是需要引起重视的一环。竖向位移的预测残差小于1.0 mm,水平位移预测残差小于0.3 mm,初步预测了基坑支护点的变化情况,达到了预期精度,因此所提出模型的预测效果能够基本满足工程项目需求。NARX动态神经网络时序结构因具备独特的时间延迟单元,符合实际工程的特性。

5 结语

本文以南宁市亭洪路72号河南水厂住宅小区危旧房改造项目双排桩基坑工程为例,结合双排桩桩顶竖向位移和水平位移监测数据,建立神经网络NARX时间序列预测模型,同时对后期变形进行了多步预测,具体结论如下:

① 采用NARX时间序列预测模型获得的基坑变形预测数据和实际监测数据的变化趋势具有较好的一致性,验证了模型的可靠性,验证了NARX动态神经网络时间序列模型用于双排桩基坑变形动态分析是可行的,可以有效解决基坑变形模糊性、非线性问题,为工程应用提供了一种解决基坑变形预测的新方法和思路。

② 本文建立的预测模型建模简单,模型稳定性好,竖向位移预测值与实际监测值的预测残差小于1.0 mm,水平位移预测残差小于0.3 mm,预测精度基本满足工程建设需要,可为今后类似工程提供借鉴。

③ 采用动态神经网络NARX时间序列模型可同时考虑多个基坑变形的影响因素,但本文建模时只考虑了开挖深度、土体暴露时间2个与时间相关联的影响因素。在接下来的研究中,可考虑地下水位变化对基坑整体的影响以及监测采样时距对预测模型精度的影响,以建立更全面更准确的基坑变形预测模型,探寻出更有效的预测方法。