自主行驶调平系统建模及自适应反步滑模控制

向洋, 蒙艳玫, 韦锦

(广西大学 机械工程学院, 广西 南宁 530004)

0 引言

根据绿篱修剪作业的实际情况,传统的燃油卡车在适应修剪需求时需要经常改变行进、倒退和停止的状态。当使用传统手动变速器的卡车底盘时,操作人员需要不断地切换卡车的油门和离合状态,不仅增加操作者的劳动强度,而且还使离合器长时间处于过度接合状态,从而导致离合器的磨损速度加快,机器故障率也随之增加。在修剪绿篱时,修剪机械手放置在承载车一边,导致承载车不仅要承受整机的重量,还受到机械手重心位置偏移引起的侧向力矩的影响。此外,机械手往复运动的惯性力也会引起周期性的侧向力矩。因为承载车有悬架,整机会在这些侧向力矩的作用下倾斜或者产生振动。这将对修剪的尺寸和形状精度产生很大的影响[1]。传统卡车底盘改造的绿篱修剪机也不易于实现自动化作业,严重制约了作业效率。基于以上现状,本文根据实验室已经研制出的车载式绿篱修剪机底盘进行改造,设计了一套以皮卡车为承载底盘的自主行驶驱动承载机构,不仅能实现绿篱修剪机的自主行驶,而且能根据修剪机机械手的侧置和路面起伏变化自适应调整整机的姿态,实现自主行驶系统自适应平衡控制。

本文设计的自主行驶调平系统通过电液比例控制系统实现对修剪机车身姿态的水平平衡调节,能够自适应路面状况和机械手侧置带来的重心偏置影响。相较于电机控制,电液比例控制系统具有诸多优点,包括反应快速、重量轻、体积小、输出推力大以及控制精度高等[2],然而,在实际的工程应用中,电液比例控制系统面临着多种问题。这些问题包括系统的非线性特性和内部参数的不确定性,还有电液调平液压缸在调平过程中负载不断变化以及受到外界环境干扰等。这些问题给控制系统的设计带来了困难,因此很多学者在这个领域进行了大量的研究[3]。通过对系统存在的负载干扰不确定性和模型非线性问题进行研究,文献[4-7]设计了一种模糊自适应比例积分微分(proportional intergal derivative, PID)控制器,并进行了仿真实验。实验结果表明,在设计的模糊自适应控制下,系统能够快速、准确地跟踪输入信号。与传统的PID方法相比,模糊PID具有更好的控制性能,具体表现为较短的系统调节时间和快速的响应,然而,模糊PID的鲁棒性相对较差,稳定性不够好。滑模变结构控制是一种非线性控制方法,在处理参数时变和外界扰动时具有稳定的特性,实现起来也非常简单,并且能够快速响应和具有很强的鲁棒性[8]。文献[9-13]中使用滑模控制方法来应对系统非线性因素的影响,并有效地解决问题,然而,滑模开关函数会导致系统发生高频切换,进而导致系统出现抖动,对控制器的输出特性产生负面影响。因此,工程实际应用上比较困难。文献[14-18]将自适应控制技术和反步设计方法相结合,消除了参数时变和外界扰动对系统性能造成的影响,在电液伺服控制、电机控制和机器人控制等领域中得到了广泛应用。

根据以上情况,本文设计了一种基于自适应反步滑模控制的自主行驶电液调平系统,以应对非线性、参数不确定性和外界环境干扰等问题。为了解决系统的非线性模型,我们将其分解成多个子系统,并选择合适的Lyapunov函数和中间虚拟控制变量。通过层层递推,最终得到系统的控制律和参数自适应律,并对误差收敛性进行了证明。仿真结果显示,该控制方法具有较快的系统响应速度,强大的自适应能力和鲁棒性,并且能够实现精确跟踪,减少了误差。

1 系统组成及工作原理

自主行驶车身电液调平系统如图1所示,系统主要由车身调平机构与电液控制系统2个部分组成。车身调平机构位于图中左半部分,主要由车架、液压缸、倾角传感器、左支撑轮和右支撑轮组成。液压缸的下端连接在支撑轮支架上,上端则连接在车架横梁上。通过车架升降液压缸的伸缩来控制车架的倾斜角度,从而实现车载式绿篱修剪机车身的自适应调平。电液控制系统由液压油箱、变量泵、单向阀、溢流阀、分流阀、电磁比例阀和控制器等组件构成。控制器通过输出信号来控制比例阀的开口大小和方向,进而实现对液压缸的伸缩控制。右侧部分即为电液控制系统的示意图。通过分流阀的同步原理,液压系统可以保证调平油缸 2、4 的进、出油量基本相同,使得2个油缸协同运动,实现调平控制机构的运动,完成整机车身的调平。通过车架上安装的倾角传感器,电液控制系统能够判断车身是否倾斜。当车身倾斜向左时,电磁比例阀6的阀芯位置在左边,而电磁比例阀7的阀芯位置在右边,这样,调平油缸2的活塞杆会向上运动,调平油缸4的活塞杆会向下运动。同时,调平油缸2、4的活塞杆会协同作用于调平控制机构,从而使得车载式绿篱修剪机车身能够保持水平,跟随调平控制机构运动。当车辆倾斜向右侧时,电磁比例阀6、7的阀芯位置与倾斜向左侧时相反,从而能够迅速调整车身平衡。在车身保持平衡的情况下,电磁比例阀6、7的阀芯将保持在中间位置,调节油缸2、4被锁定,而电磁换向阀13则会实现卸荷操作,这样就能确保车身一直保持水平。

1-左支撑轮;2-左液压油缸;3-车架;4-右液压油缸;5-右支撑轮;6、7-电磁比例阀;8-液压油箱;9-分流阀;10-溢流阀;11-单向阀;12-变量泵;13-电磁换向阀。图1 自主行驶车身电液调平系统Fig.1 Structure diagram of the autonomous vehicle body electro-hydraulic leveling system

2 电液调平系统非线性模型

图1中的θd为角度参考给定值,θ为输出反馈值,系统通过控制输入信号u,控制输出角度信号θ跟踪指定角度信号θd。车身调平机构中液压缸输出位移xp与角度θ的关系式由几何关系可以求出。根据自主行驶电液调平系统中几何关系与液压系统理论,建立电液调平方程。

① 车身调平机构动态方程为

xp=lsinθ,

(1)

式中l=OA=OB,是车架宽度的一半。

② 比例阀流量方程为

(2)

式中:ρ是液压油密度;PS是液压泵出口压力;PL是负载压力;xv是比例阀芯位移;QL是负载流量;ω是比例阀面积梯度;Cd是阀口流量系数。其中比例阀芯位移xv与输入u之间可以等效为比例关系,xv=kpu,其中kp为比例阀增益。

③ 车架升降液压缸流量方程为

(3)

式中:βe为油液有效体积弹性模量;V是液压缸进回油侧总体积;Ct是液压缸外泄漏系数;AP是液压缸活塞有效面积。

④ 活塞力平衡方程为

(4)

式中:FL是作用在液压缸活塞上的外负载力;k是负载的弹性刚度系数;BP是活塞和负载的黏性阻尼系数;Mt是活塞与负载的总质量。

根据式(2)—(4),最终得电液调平系统状态方程,取状态

其中x1、x2、x3分别为液压缸活塞的位移、速度和加速度。

(5)

式中:

系统的不确定性F主要包括参数不确定性和外界干扰部分,这些不确定性会对系统的输入和输出产生影响。u为系统输入,y为系统输出。

3 自适应反步滑模控制器设计

① 定义活塞杆位置跟踪误差为

e1=x1-x1d,

(6)

对e1求导得

(7)

取Lyapunov函数为

(8)

对式(8)求导得

(9)

② 定义误差变量e2=x2-x2d,其中x2d为虚拟控制量,取

(10)

代入式(9)得

(11)

对e2求导有

(12)

取Lyapunov函数为

(13)

对式(13)求导有

(14)

③ 定义误差变量e3=x3-x3d,其中x3d为虚拟控制量,取

(15)

代入式(14)得

(16)

④ 与滑模控制相结合,在算法的最后一步,定义滑模面为

s=c1e1+c2e2+e3,

(17)

式中c1、c2为大于0的常数,且满足多项式p2+c2p+c1为Hurwitz。

对式(17)求导有

(18)

(19)

对式(19)求导得

(20)

令ξ1=a1a4、ξ2=a2a4、ξ3=a3a4、ξ4=a4(a5+F),则式(20)可以化简为

(21)

⑤ 加入自适应控制,实现参数估计

(22)

其中δi>0(i=1,2,3,4,5)。对式(22)求导有

(23)

自适应滑模控制器取为

(24)

控制器使用饱和函数sat(s)来替代理想滑动模态中的符号函数sgn(s),以减弱系统的抖振。此处,ε>0,η>0且为常数

(25)

在该公式中,函数边界层φ被分为2个部分:边界层外部采用切换控制方法,而边界层内部则采用线性化反馈控制。

(26)

(27)

式(23)可以化简为

(28)

(29)

将式(29)代入式(28)得

(30)

其中:E=(e1,e2,e3)T;

下面对系统跟踪误差的收敛性进行证明。

定理1对于电液比例非线性系统(5),参数自适应律为式(29),本文设计的控制器为式(24),选用合适的控制器参数c1、c2、k1、k2和ε,只要满足以下不等式:

(31)

则整个系统是渐近稳定的,意味着系统的位移跟踪误差将会收敛。

证明当控制器参数c1、c2、k1、k2和ε满足式(31)时,矩阵Q的一、二、三阶顺序主子式全部大于0,从而得出该矩阵Q正定。

因为e1、e2、e3以及

4 仿真验证与分析

根据自主行驶电液调平系统的实际工况,给出电液调平系统模型参数值(见表1)。

表1 模型参数Tab.1 Model parameters

考虑到自主行驶电液调平系统作业时的实际工况,给出参考角度输入信号为θd=20°的阶跃信号,因为控制器设计的是跟踪液压缸活塞杆的位移,所以可以通过公式(1)得到液压缸活塞杆位移参考曲线xp。在调平过程中,系统内部参数,如负载质量和黏性阻尼系数等,会在工作状况改变时缓慢变化,特别是负载的弹性刚度系数很难准确获得数值时。弹性外负载力会随车身倾斜的变化而改变。假设这些变化为某一不确定性,将该不确定性设为系统的总不确定性。假设外负载力变化为FL=FL0+0.1FL0sin(πt),设系统总的不确定性为F=5 000 sin(πt)。

采用MATLAB/Simulink软件平台进行仿真研究,验证本文设计的自适应反步滑模控制器的有效性和鲁棒性。所设计的控制器采用特定的自适应律参数,并进行了相应的调整。设计的控制器与自适应律参数选为:k1=500,k2=600,ε=450,η=5,c1=1,c2=2,δ1=30,δ2=500,δ3=400,δ4=5,δ5=90。

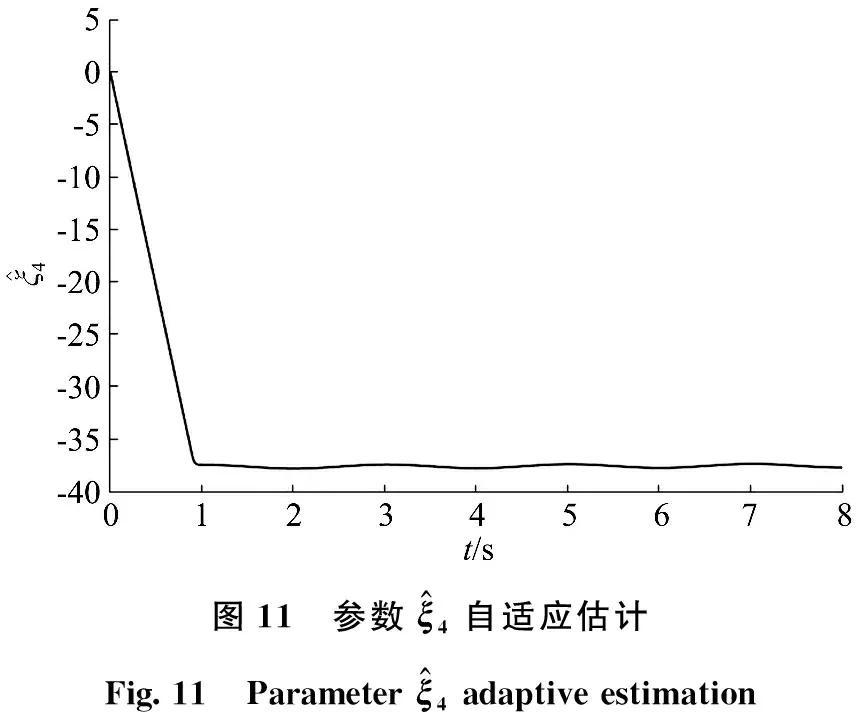
在本仿真实验中,我们将系统的初值设定为0,并通过仿真验证得到了以下结果。角度跟踪曲线比较如图2所示。从图2中可以明显看出,自适应反步滑模控制器的性能要优于传统PID控制器的性能。在本文提出的控制器的作用下,系统大约在1.2 s就达到了平衡状态,比PID控制器快了整整5倍。2种控制器跟踪误差的比较如图3所示。由图3可知,2种控制器跟踪误差都在1°以内,本文设计的控制器跟踪误差更小。图4、图5是2种控制器的输入曲线。从图4、图5可知,自适应反步滑模控制的输入要略大于PID控制输入,与实际情况相符合,本文设计的控制器控制精度更高,响应更快,但相应输入会更大。通过观察图5,我们可以得出结论:在实际工程应用中,滑模控制存在抖振问题。针对这个问题,本文采用了一种用饱和函数替代传统滑模控制中符号函数的思想,通过这种方法使得控制输入变得平滑,有效地减弱了系统的抖动。图6展示了在系统存在不确定情况下自适应反步滑模控制器滑模面趋近的过程。图7至图11展示了具有不确定参数的自适应估计曲线。通过观察这些图可以得出结论,不确定参数的自适应估计是有界的。控制器可以根据系统的不确定性和外界干扰进行相应的调整,从而使系统具有良好的适应性和强鲁棒性。

图2 角度跟踪曲线比较Fig.2 Comparison of angle tracking curves

图3 角度跟踪误差曲线比较Fig.3 Comparison of angle tracking error curves

图4 PID控制输入电压Fig.4 Input voltage of PID control

图5 自适应反步滑模控制输入电压Fig.5 Input voltage of adaptive backstepping sliding mode control

图6 滑模面趋近过程Fig.6 Sliding surface approaching process

5 结论

本文设计了一种基于自适应反步滑模控制的自主行驶电液调平系统,该系统通过倾角传感器来测量车身的倾斜角度,并通过控制器计算得出的结果控制电磁比例阀的开口大小,从而驱动左、右液压缸的升降,最终实现绿篱修剪机车身的自动调平功能。应用相关的动力学分析,可以建立一个非线性模型来描述电液调平系统。这个系统面临着非线性、参数不确定性以及来自外界环境的干扰等问题。为了解决这些问题,我们设计了一个自适应反步滑模控制器,该控制器可以有效地克服系统参数不确定性和外界环境干扰所带来的影响。同时,该控制器具备很强的自适应性和鲁棒性。通过仿真验证得出:相较于传统PID控制方法,采用自适应反步滑模控制方法在控制性能方面更具优势。通过采用自适应反步滑模控制方法,系统调平时间缩短了1/5,误差保持在1°以下。此外,该方法还表现出很强的鲁棒性,并且调平过程非常稳定。