电动汽车轮毂的结构优化

陈伟

（盐城生物工程高等职业技术学校，盐城 224000）

汽车部件的安全性一直是科研人员关心的焦点。轮毂是汽车行驶系统中的一个关键旋转组件[1]，在确保轮毂安全性能的基础上对其结构进行优化显得尤为重要。

自然界中的蜂窝结构作为一种典型的轻质、高强结构，具有类似轮毂弯曲典型工况受力方式的受力特征[2]。文章利用蜂窝结构开展车轮轮辐部位仿生设计研究，将响应面优化法应用于蜂窝轮毂优化设计，完成轮毂的优化设计，并预测其疲劳寿命。

1 基于蜂窝结构的轮毂仿生设计

自然界中的蜂窝结构主要承受轴向力的作用。通过不断演化，当蜂窝结构受轴向载荷时，蜂窝内部应力和变形较小，从而保护了蜂窝内部虫卵安全[3]。蜂窝具有类似于轮毂弯曲典型工况受力方式的受力特征，因此基于蜂窝结构重新设计了轮辐位置。蜂窝仿生轮毂如图1 所示。

2 仿生轮毂性能分析

2.1 蜂窝仿生轮毂与普通轮毂的性能对比

由于轮毂的特殊对称结构，在轮毂弯曲载荷的作用下进行了2 种工况分析，工况1 为轴端载荷经过轮辐，工况2 为轴端载荷经过轮辐中部。不同弯曲载荷工况下的仿生轮毂和普通轮毂的有限元计算结果如图2 所示。

初步设计出的2 种仿生轮毂在2 种不同工况下最大应力均发生在轮辐根部。2 种轮毂结构弯曲载荷真结果如表1 所示。由表1 可知，与普通轮毂相比，生轮毂的质量减少33.6%，尤其是轮辐位置减少最为显。仿生轮毂的最大应力未超出轮毂材料许用应力范围但同一弯曲工况下，其最大应力相较于普通轮毂有所加，疲劳寿命降幅过大，性能达不到国标要求[4]。

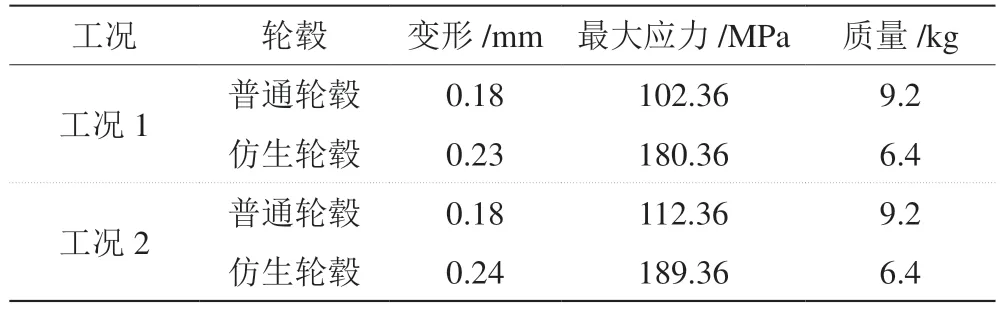
表1 2 种轮毂结构弯曲载荷仿真结果

2.2 仿生轮毂结构优化设计

为满足轮毂疲劳寿命的要求，在轮毂应力集中位加装环形加强筋。对设计出的仿生轮毂进行初步化，在确保安全性的前提下尽量实现轮毂结构轻量化优化后的模型如图3 中所示。

图3 仿生轮毂初步优化模型

3 蜂窝仿生轮毂响应面优化设计

3.1 设计参数确定

在轮毂响应面优化过程中，主要针对轮毂局部尺寸进行优化。轮毂中包含大量参数，为更精确地找到响应面目标参数中最重要的优化参数，本研究尝试性地选取了5 个影响大、加工难度低的参数，作为灰色关联度的分析对象。5 个参数分别为环形加强筋厚度X1、加强筋与法兰面距离X2、轮辐蜂窝壁厚X3、减重孔壁厚X4以及轮辐蜂窝孔内径X5，如图4 所示。

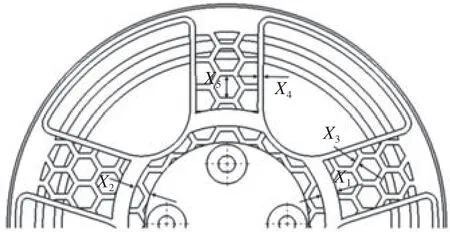
图4 轮毂初步设计参数

灰色关联度分析本质上属于相对性排序分析，数学模型比较简单，适用于求解多变量的复杂系统[5]。运用MATLAB 软件中的灰色关联度分析，分析初选的5 个优化参数。优化因素对所选弯曲载荷最大等效应力和轮毂质量的关联度如表2 所示。选择关联度较高的参数加强筋到法兰面的距离X2、减重孔壁厚X4和轮辐蜂窝孔直径X5，作为响应面分析优化参数，从而简化计算过程。

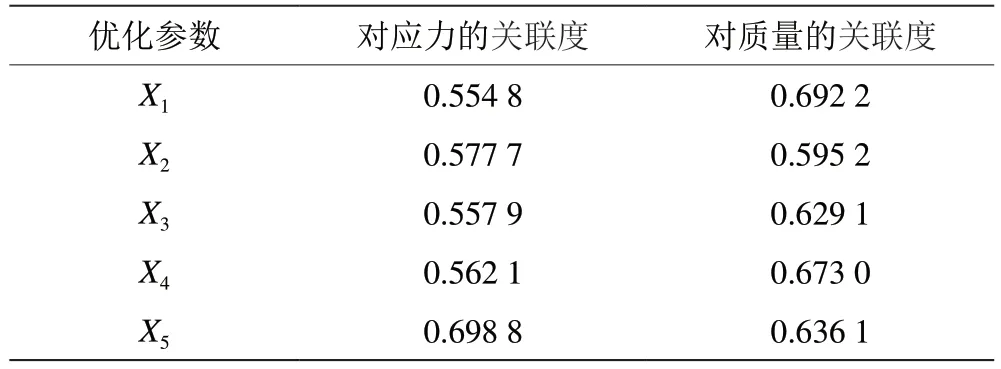
表2 优化参数对应力及质量的关联度

3.2 响应面法实验设计

在响面应优化过程中，实验设计尤为重要。本实验采用Box-Behnken 设计方法，以X2、X4、X5为分析优化参数，以弯曲载荷工况2 中出现的最大等效应力最小为目标。优化参数的一般取值范围为初始设计值±10%，如表3 所示。

表3 优化参数变化范围

3.3 响应面模型分析

建立仿生轮毂的弯曲疲劳载荷有限元模型，对其进行弯曲载荷有限元分析。由于最大等效应力出现在工况2 中，在工况2 下进行仿真计算，结果如图5 所示。弯曲载荷模拟结果表明，优化后仿生轮毂的最大变形为0.18 mm，最大等效应力为113.09 MPa，小于轮毂材料的许用应力。

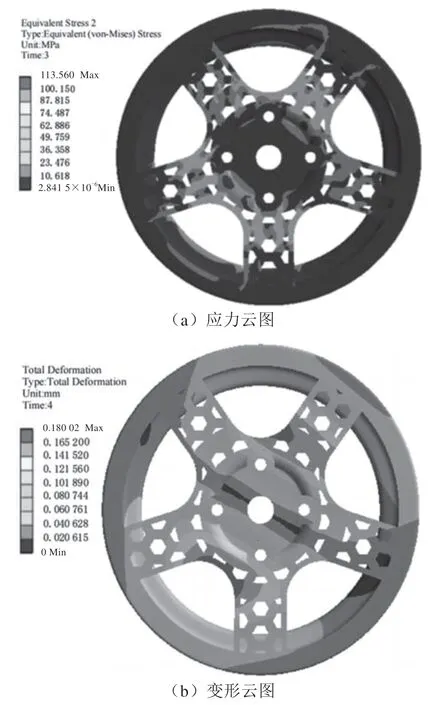
图5 响应面优化后工况2 下的仿生轮毂仿真结果

3.4 优化后疲劳寿命预测

将优化后仿生轮毂的有限元模拟计算结果导入NCode 疲劳计算软件，运行疲劳寿命分析流程求解结果。图6 为疲劳寿命预测结果，优化后仿生轮毂的最小循环次数约为1.72×105次，达到国标规定的商用汽车轮毂的最小循环次数。与经过拓扑优化的轮毂相比，蜂窝式仿生轮毂的质量减轻了约23%，质量减轻主要发生在轮辐位置。

图6 优化后仿生轮毂疲劳寿命预测结果

4 结语

由于蜂窝结构具有轻质、高强等结构特征，采用蜂窝结构对轮毂结构进行仿生优化设计，并对轮毂轮辐进行再设计。对比不同工况下不同轮毂的性能指标，并对优化后的蜂窝仿生轮毂模型进行弯曲载荷仿真分析，发现仿生轮毂的最大等效应力增加过多，最低循环次数减少过多，不符合国标要求，未达到轮毂优化目的。采用响应面分析法确定了轮毂最优尺寸参数，进行进一步优化。最终优化后蜂窝仿生轮毂的最小循环次数约为1.72×105次，满足国标对商用汽车轮毂弯曲疲劳寿命的要求。