表征被动双足行走的二维无边轮辐的动力学及稳定性分析
奚如如 王兴松 韩亚丽
(1 东南大学机械工程学院,南京211189)
(2 南京工程学院机械工程学院,南京211167)
被动双足行走指的是双足行走机构只依靠本身结构、重力、足与地面的摩擦力及碰撞力而实现双足行走[1-2].被动行走机构不包含可以将系统非机械能转换为机械能的部件(如电机等),但可以包含如弹簧阻尼之类的储能元件.基于被动行走理论的双足机器人是欠驱动的,实现自然状态下的行走运动,无附加驱动力而产生的能量损耗.被动行走研究的主要思路是首先研究无驱动的纯被动机器人[3].现有简单类双足机构二维无边轮辐模型,可在斜坡上滚动,通过间歇性碰撞实现相对持续的运动.简单无驱动被动双足行走模型[1-2]的支撑腿与摆动腿通过自由铰链连接,支撑腿呈现倒立摆行走特性,摆动腿以自由铰链为节点自由摆动.轮辐支撑辐条的运动及其与斜坡间的碰撞分别对应双足行走模型支撑腿的运动及其摆动腿与斜面的碰撞,随着碰撞的发生,轮辐两相邻支撑辐条完成交替,且对应于双足模型支撑腿与摆动腿的交替.轮辐的运动具有纯被动特性,呈现了人类行走过程中足与地面的接触及支撑腿与地面的类似倒立摆的相对运动,对其动力学及相邻辐条间碰撞交替的研究对被动行走本质的探究更具直观性.
McGeer[1-2]最先基于无边轮辐的运动特质提出被动双足行走理论,并对无边轮辐运动及其稳定性进行了初步理论分析.文献[4-9]基于McGeer提出的具有被动行走特性的无边轮辐模型,对被动双足行走机器人进行了深入的研究.文献[5-13]指出无边轮辐系统是包含连续动力学与离散动力学的复合系统.文献[14-19]虽对无边轮辐运动及其被动特性进行了基本描述和运动仿真,但对动力学特性的数值分析、轮辐运动极限环、初始条件及机构参数之间的相互依存关系没有进行直接深入的研究,从而限制了对其动力学特性的直接应用.
本文对无边轮辐模型进行动力学特性分析,揭示轮辐实现稳定被动行走的可能性、影响因素及其所依据的数值关系.基于倒立摆模型及角动量矩守恒原理建立表征无边轮辐模型的运动学方程及碰撞瞬间切换方程,利用庞加莱截面及映射理论对斜坡上的无边轮辐进行运动稳定性分析.结果表明,具有复合动力学特性的轮辐系统在特定条件下可实现稳定持续的下坡滚动,不动点与极限环的存在是轮辐运动稳定性的主要表征参数.不动点与极限环的存在与轮辐的辐条数目、惯性矩参数、运动初始条件和斜坡角度有关,验证了一定的斜坡角度和初始角速度下的轮辐可实现稳定持续的下坡滚动.本文对轮辐运动不动点及极限环的数值研究方法具有普遍适用性,可直接指导无驱动双足被动行走模型的研究.若将轮辐下坡时重力利用等同于双足机器人的驱动力,则对以固有频率行走、减少驱动能耗及简化控制理论为目标的主动双足行走及下肢外骨骼的步态规划及机构研制具有借鉴意义.
1 无边轮辐系统模型
1.1 系统模型及运动参数配置
如图1所示,无边轮辐模型成轴对称分布,质量为m,质心点C,转动惯量为IC,辐条分布均匀,辐条总数为n,辐条长度为l,相邻辐条之间的角度为β=2π/n,斜坡角度α.滚动过程中当前接触地面的辐条定义为支撑辐条,辐条角度θ 定义为辐条相对于地面垂直线的角度,逆时针方向为正.
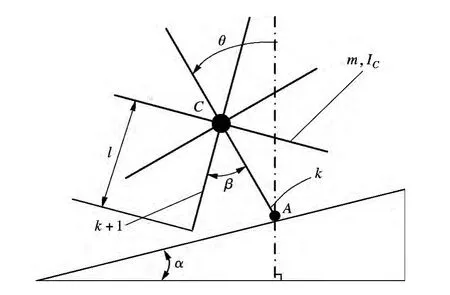
图1 无边轮辐系统模型
为了更好地研究无边轮辐运动特性,作如下假设:①当前支撑辐条端点与坡面的接触点相当于铰链链接点;②辐条与坡面间的碰撞为非弹性且瞬时完成,无滑移和弹起现象;③辐条与坡面碰撞瞬间无冲击,两相邻辐条分别平稳地接触和离开斜坡;④辐条端点与坡面接触点之间的摩擦力损失忽略不计[5-7].
鉴于上坡和下坡现象在无边轮辐运动过程中可能交替出现,需对轮辐运动参数标示明确.
1)为避免模运算,辐条表征参数k 采用逐一计数模式,k=0 定义为无边轮辐与地面的初始状态.无边轮辐从k=0 辐条开始运动,逆时针运动时首个支撑辐条记为k=1,顺时针运动时首个支撑辐条记为k= -1,依次加减1 类推.
2)i 表征碰撞次数,i=0 为初始状态,i 采用逐一计数方法,每发生一次碰撞,i 加1,0≤i≤+∞.j(i)表征第i 次碰撞后的支撑辐条,支撑辐条随着每次碰撞的发生而改变.轮辐历经i+1 次碰撞后,若其为逆时针下坡运动,支撑辐条j(i +1)=j(i)+1;反之,j(i+1)=j(i)-1.
3)上标(-)和(+)表征碰撞前后瞬间.记ti为第i 次碰撞发生时刻,t+i为第i 次碰撞后瞬间,为第i 次碰撞前瞬间,θk(t)为辐条k 在t 时刻的角度,θk(ti)为辐条k 在ti时刻的角度.
4)鉴于无边轮辐与双足行走特性的研究相关性,仅考虑当前支撑辐条而不是所有辐条的运动状态,轮辐当前支撑辐条运动特性对应于双足行走机器人的支撑腿.记(t)为轮辐第i 次碰撞后支撑辐条j(i)在任意时刻t 的角度,为第i 次碰撞后瞬间支撑辐条j(i)的角度,其与意义相同.类似地,
1.2 模型运动周期及分析
如图2所示,无边轮辐在角度为α 的斜坡上作下坡运动,支撑辐条以逆时针方向滚动.如图2(a)、(b)、(e)、(f)所示,碰撞发生后瞬间,无边轮辐分别以(iθ+,i+)与(i+1θ+,i+1+)作为初始条件进入无碰撞阶段,运动至下一次碰撞发生.如图2(d)所示,轮辐支撑辐条呈竖直状态,即支撑辐条角度为零,整个轮辐机构关于支撑辐条对称.如图2(c)、(d)、(e)所示,无边轮辐处于无碰撞阶段,整个轮辐的运动可看作是以角度iθ+=α -π/n、角速度i+作为初始条件的非完整周期的倒立摆运动,终止于边界条件i+1θ-=α +π/n.由图2(a)、(b)、(c)可知,无边轮辐整体参数配置在碰撞前后无显著变化,但支撑辐条在碰撞前后完成j(i)与j(i +1)两相邻辐条的交替,支撑辐条角度发生幅度为±2π/n 的跃变,且因碰撞引起轮辐整体动能损耗,导致碰撞前后轮辐角速度变化很大.显然,碰撞前后的支撑辐条角度与角速度均不连续.
当无边轮辐作上坡运动时,支撑辐条沿顺时针方向滚动,可从左向右依次逆解读图2中轮辐运动状态来说明.图2(b)、(f)为碰撞瞬间,碰撞点分别为点A 和点D,图2(a)、(e)为碰撞前瞬间,图2(c)为碰撞后瞬间,图2(d)为支撑辐条呈竖直状态.图2(c)、(d)、(e)中的轮辐处于无碰撞阶段,其参数配置方式的遵循原则与下坡运动时保持一致.
无边轮辐无论处于何种初始运动趋势,在运动过程中其运动趋势均可能出现翻转.轮辐到达如图2(d)支撑角度为零状态时,角速度将决定轮辐是否可以通过支撑辐条来达到竖直状态,从而影响轮辐是否继续初始运动或出现摇摆运动.
因此,本文定义无边轮辐一个完整的运动周期为一个完整的无碰撞运动过程和接下来的一次碰撞运动,并在不改变模型参数意义的基础上简化角度及角速度的符号标示,以当前支撑辐条角度θ(t)、角速度(t)作为研究对象,研究无边轮辐的运动特性.一个完整的轮辐运动周期可表现为上坡运动、下坡运动或组合运动,即在一个运动周期内,轮辐运动趋势可能发生改变,或出现摇摆现象.
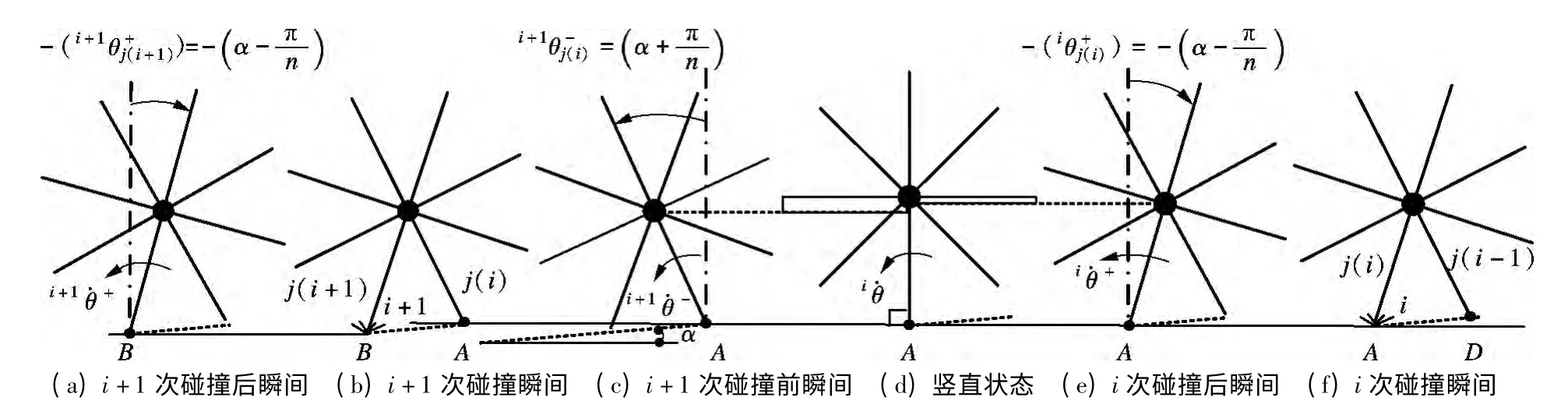
图2 无边轮辐模型运动状态示意简图
2 系统动力学分析
2.1 运动方程
如图2(c)、(d)、(e)所示,无论轮辐初始运动趋势为上坡或下坡运动,轮辐都处于无碰撞运动阶段,整个轮辐关于支撑点A 的角动量矩平衡,即

式中,MA为轮辐关于点A 的所受力矩总和;˙HA为轮辐关于点A 的角动量变化率.
由式(1)可得无碰撞阶段的无量纲运动方程为
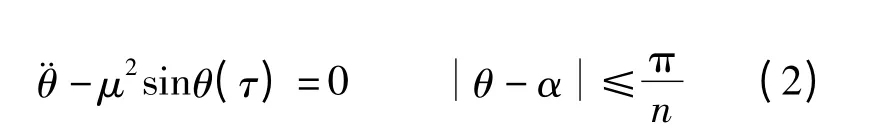
2.2 碰撞瞬间切换方程
轮辐碰撞前后瞬间参数配置如图2(a)~(c)所示,支撑辐条角度在碰撞前后有±2π/n 的跃变.无边轮辐在碰撞发生前为逆时针下坡运动,轮辐碰撞后瞬间相对于碰撞前瞬间转过了-2π/n 角度;反之,若轮辐在碰撞发生前呈顺时针上坡运动趋势,轮辐则转过2π/n 角度.第i 次碰撞前后瞬间角度跃变公式为

无边轮辐在碰撞发生前为逆时针下坡运动,iθ-=α+π/n,iθ+=α -π/n;反之,若无边轮辐在碰撞发生前为顺时针上坡运动,则iθ-=α -π/n,iθ+=α+ π/n.无论何种运动趋势下发生碰撞运动,碰撞前后含符号函数的角度跃变公式(3)均可改写为如下简单形式:
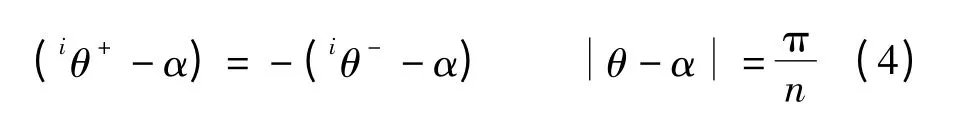
无边轮辐的角速度随着碰撞的发生而改变,忽略重力及碰撞瞬间对轮辐引起的冲击,则整个轮辐关于点B 角动量守恒,即

式中,H-B 为第i 次碰撞前瞬间轮辐关于点B 的角动量;H+B为第i 次碰撞后瞬间轮辐关于点B 的角动量.
由式(5)可得第i 次碰撞前后瞬间角速度跃变方程为

式中,碰撞参数λ=1 + μ2(cos(2π/n)-1),0 ≤λ <1.
第i 次碰撞前后瞬间角度、角速度跃变公式(4)、(6)表征了碰撞发生前后轮辐支撑辐条运动参数的改变,式(4)、(6)可统称为碰撞瞬间切换模型.
2.3 关键角速度临界值
引进临界角速度参数dn和up,获取依据为无边轮辐介于2 次碰撞之间的运动遵循能量守恒原则.在一个运动周期的无碰撞阶段,轮辐以一定的初始角速度运动,轮辐的初始动能可根据图2(c)、(d)、(e)中的动能和势能表征条转换.在θ=0 处完全转化为势能,即在θ=0 处,轮辐角速度亦为零,此时轮辐处于基于1 个支撑辐条的不稳定竖直平衡状态.
当无边轮辐呈下坡运动趋势时,轮辐以临界角速度dn作初始运动,可根据图2(d)与(e)间的能量表征条进行能量转换;反之,当轮辐呈上坡运动趋势时,轮辐以临界角速度up作为初始速度运动,根据图2(c)与(d)间能量表征条进行能量转换,计算可得

无边轮辐呈下坡运动趋势且碰撞后瞬间角速度为dn或上坡运动趋势且碰撞后瞬间角速度为时,轮辐将耗时无限长到达并停留在位置θ=0处,轮辐基于1 个支撑辐条竖直静止,是一种临界不稳定平衡状态.
2.4 相图及运动轨迹流
无碰撞阶段的运动方程式(2)可改写成如下一阶微分方程组:

积分后可得介于2 次碰撞之间的相空间轨迹流,即
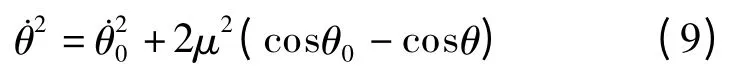
鉴于支撑辐条与斜坡之间的空间限制,支撑辐条并不能进行完整的倒立摆运动,因此无边轮辐的轨迹变化需在相空间U 中进行研究,即
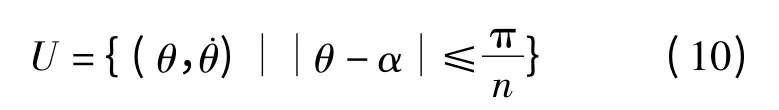
无碰撞阶段运动方程式(8)及碰撞瞬间切换模型(4)、(6),均可表达为如下形式:


2)图3中相空间U 内的连续运动轨迹流,根据独立向量场v 发生连续变化,表明轮辐在无碰撞阶段的动力学特性.相空间边界∂U 上的碰撞切换轨迹流,依据独立向量场h 发生离散性质的跳跃变化,表明轮辐碰撞发生前后支撑辐条角度与角速度的跃变.一个完整的运动周期轨迹流为连续运动轨迹流与相应的碰撞切换轨迹流的组合,具有连续动力学与离散动力学并存的复合动力学特性.
3)以所属相空间边界∂U 内含临界值的边界点x1(α-π/n,dn)与x2(α +π/n,up)为初始条件的临界运动轨迹流终止于不稳定平衡位置θ=0处,轮辐不再出现后续运动轨迹流.当轮辐连续滚动时,轮辐上一次碰撞后瞬间(θ,)即为轮辐下一个运动周期的初始条件.若轮辐历经数次碰撞后,其运动参数达到临界边界点,则轮辐将到达并停留在θ=0 位置,轮辐将不会发生下一次碰撞.
4)如果斜坡角度α >n/π,轮辐角度θ 始终大于零,则相空间内不包含不稳定竖直平衡状态θ=0.

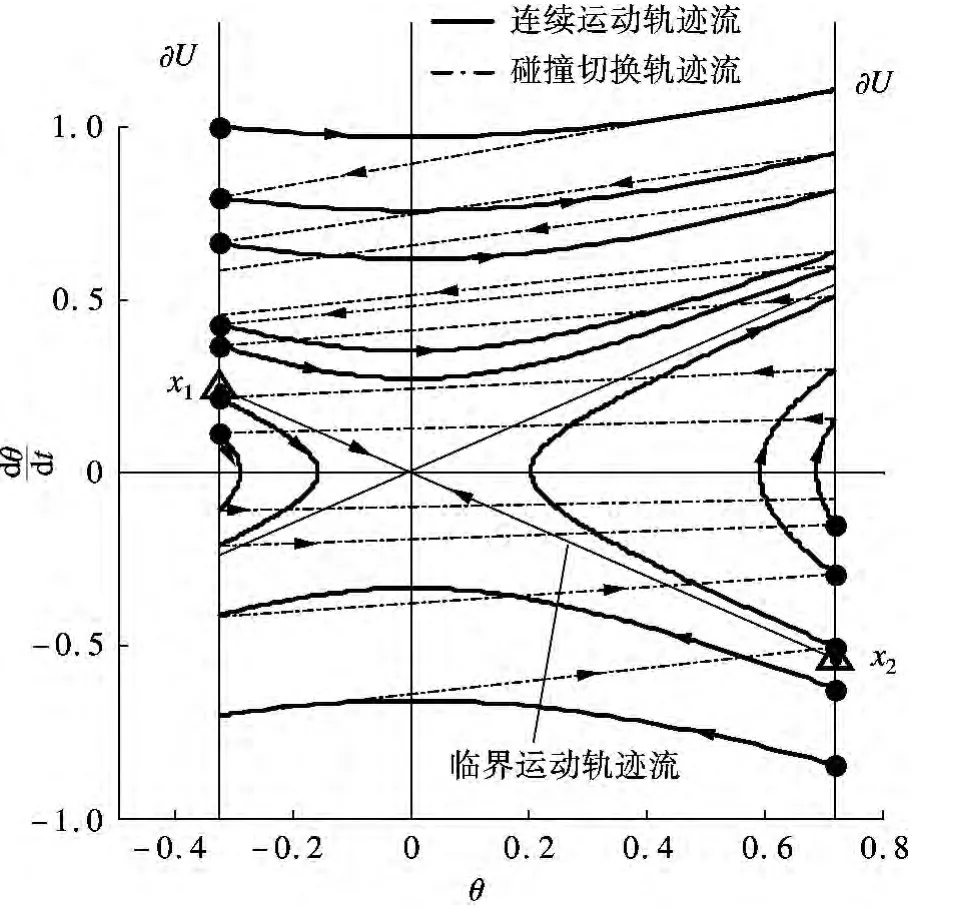
图3 两次碰撞间的相空间轨迹流图
以满足式(13)的边界点为初始运动条件,图3中连续运动轨迹流表明,轮辐均未通过θ=0 位置,而是逆向终止于相空间边界∂U 上,轮辐出现运动趋势发生逆转的摇摆运动.反之,若(θ,)满足

以满足式(14)的边界点为初始运动条件,图3中相空间U 内连续运动轨迹流均都正向终止于相空间边界∂U 上,轮辐运动趋势保持不变.
6)无论轮辐以何种初始条件运动,历经数次碰撞、上坡、摇摆及下坡运动后,轮辐可能处于如下3 种状态:①基于单个支撑辐条上的竖直状态,即运动轨迹流终止于不稳定平衡位置;②基于两相邻支撑辐条上的稳定静止状态,即运动轨迹流终止于相空间边界∂U 内的=0 边界点上;③轮辐以一定速度作持续下坡滚动.如图4所示,设n=6,α=π/16,μ=0.75,轮辐以θ0=α -n/π,0=1 为初始条件开始运动,历经足够多次碰撞后,连续运动轨迹流与碰撞切换轨迹流逐渐成为闭合曲线,说明极限环在特定条件下是存在的,轮辐可以实现稳定持续的下坡滚动.

图4 无边轮辐相空间轨迹流及极限环
3 系统不动点及稳定性分析
3.1 庞加莱截面
利用庞加莱回归映射方法研究轮辐系统不动点、极限环的影响因素及存在条件,从而判定轮辐是否可实现稳定持续的下坡滚动[5-7].庞加莱截面Γ 定义为

3.2 庞加莱回归映射
建立如下庞加莱映射关系:

式中,iq+=(iθ+,i+)∈Γ,映射函数f:Γ→Γ,f=(h ◦v)是基于离散向量场h 和连续向量场v 的复合映射,向量场h 与v 有如下关系:




映射函数P 表示轮辐第i 次碰撞后与第i +1次碰撞后的角速度之间的关系.如式(19)所示,当0≤α≤π/n 时,函数P 是受临界值dn,up和参数集合ψ={μ2,n,α}影响的分段连续函数,从而轮辐在运动过程中会出现交替上坡运动、下坡运动及包含2 种运动的摇摆运动;如式(20)所示,当π/n<α≤π/2 时,函数P 是受参数集合ψ={μ2,n,α}影响的连续线性函数,若将无边轮辐两相邻辐条支撑于斜坡上,即使给轮辐零初始角速度或上坡运动趋势,轮辐最终仍会自主持续下坡滚动.
3.3 映射函数的不动点
映射函数P 表征了轮辐相邻2 次碰撞后瞬间角速度之间的关系,函数P 的不动点的存在意味着轮辐历经数次碰撞后,其后每次碰撞后的瞬间角速度值均相同,这表明轮辐运动存在极限环,由式(19)、(20)可得函数P 的不动点ω*.
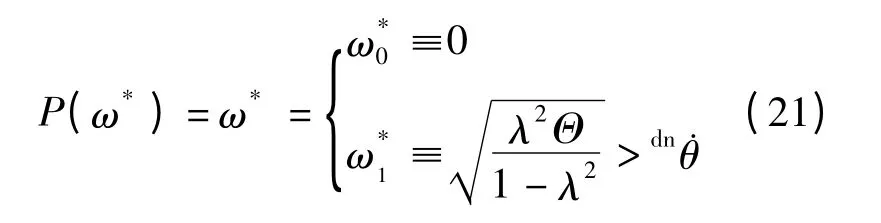

式中,ω0*为静止不动点,表明轮辐最终可实现基于两相邻辐条支撑的稳定静止状态;为极限环不动点,表明极限环的存在及轮辐最终可实现持续稳定的下坡滚动,即轮辐历经数次碰撞后角速度值趋向且最终等于,其后每次碰撞后的瞬间角速度值均等于ω*1.
3.4 不动点存在的影响因素
由不动点表达式(21)、(22)可知,不动点的存在与轮辐自身模型参数μ、轮辐数目n 及斜坡角度α 有关.当轮辐模型参数一定时,函数P 的2 个不动点ω0*与ω*1与斜坡角度的关系为
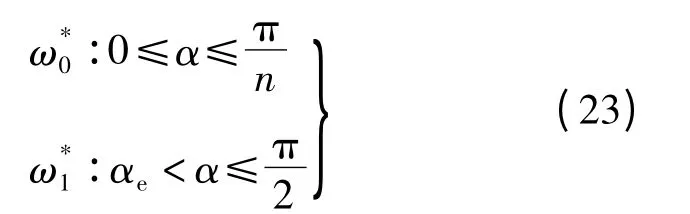
式中,αe为临界斜坡角度,是决定极限环不动点ω1*存在与否的临界值,由式(21)可推出αe满足

由图5可知,不同的斜坡角度对应不同的一维回转图,不动点性质及存在个数也不同.
如图5(a)所示,当0≤α≤αe时,轮辐存在静止不动点ω*0及表征不稳定平衡位置的临界值up和dn,不存在极限环不动点ω*1 ,轮辐最终处于稳定静止状态或不稳定平衡状态.
如图5(b)所示,当αe<α≤π/n 时,轮辐存在静止不动点ω0*、极限环不动点ω1*及临界值和等.轮辐以不同的初始条件运动,历经数次碰条件取决于角速度临界值撞,轮辐角速度逐渐趋向于ω0*,ω1*,up或dn等4种角速度值,此时轮辐最终运动状态可能有3 种:①轮辐基于两相邻辐条摇摆数次,角速度在有限时间内衰减至静止不动点ω*0,轮辐最终静止于两相邻辐条上;②轮辐碰撞后瞬间角速度值以增速和减速2 种方式逐渐趋向且最终等于极限环不动点ω1*,轮辐实现以ω1*为运动角速度的稳定持续的下坡滚动;③碰撞后瞬间轮辐角速度达到临界值up和dn,然后轮辐将耗时无限长到达并停留在竖直位置,即不稳定平衡状态θ=0 位置.

图5 不同斜坡角度对应的不动点与相应的一维回转图(n=6,μ=0.75)
3.5 不动点稳定性判据
不动点的稳定性由映射函数在不动点处的一阶导数决定.函数P 在不动点ω*0与ω*1处的一阶导数为

由于0≤λ <1,映射函数P 在不动点ω*0与ω1*处的一阶导数DP(ω*)满足因此,映射函数P 的不动点ω*0与ω*1是渐进稳定的.
3.6 不动点的吸引盆
当α=π/15,n=6,μ=0.75,回转图如图6所示.图6表示了轮辐静止不动点ω*0与极限环不动点ω*1及临界值dn和up等均存在时的多种运动状态.静止不动点ω*0与极限环不动点ω*1交替吸引相应区域内的初始条件,从而决定轮辐运动状态.吸引盆在回转图中表现为不同区域内的线段,吸引盆的边界由角速度临界值来界定.图6中奇数值区域内线段为极限环不动点的吸引盆,偶数值区域内线段为静止不动点的吸引盆.由此可知,满足极限环存在的初始所界定的区域,且不动点ω*0与ω*1相对应的吸引盆交替出现.

图6 临界角速度值与相应不动点的回转图
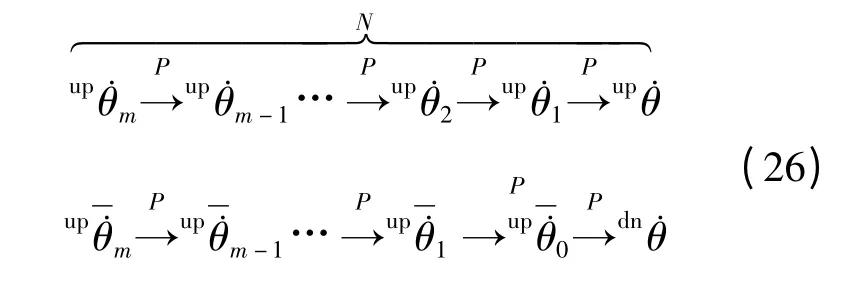
当轮辐以式(26)中临界值系列为初始条件开始运动时,其终止于θ=0 位置而无法到达任一不动点,由映射函数P 可推导出m≥1 时的系列临界值,其表达式为
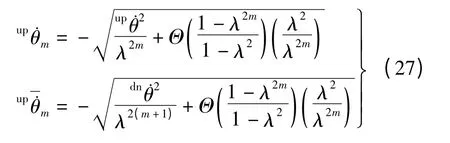
综上所述,轮辐最终所处运动状态依赖于斜坡角度及由临界角速度值界定的不动点ω0*与ω1*吸引盆内的初始角速度.斜坡角度、初始角速度与不动点类型的具体依存关系如表1所示,轮辐最终运动状态与初始运动趋势如图7所示.①若轮辐初始角速度或历经数次碰撞后的角速度为临界角速度值,无论斜坡角度如何,轮辐终将处于不稳定竖直状态;②当斜坡角度为0≤α≤αe时,初始角速度为非临界角速度值,所有角速度值都位于静止不动点ω*0的吸引盆内,即无论轮辐为何种初始运动趋势,轮辐终将历经M 次摇摆后基于两相邻支撑辐条处于稳定静止状态;③当斜坡角度满足αe<α≤π/n,且角速度满足或则所有角速度值都位于静止不动点ω*0的吸引盆内,即轮辐历经M 次摇摆后将基于两相邻支撑辐条处于稳定静止状态;④当斜坡角度满足αe<α≤π/n 且初始角速度满足则角速度值均位于极限环不动点ω1*的吸引盆内,轮辐由最初的上坡滚动通过一次摇摆逆转为下坡滚动,历经数次碰撞,轮辐角速度最终增速趋向并等于极限环不动点ω*1,轮辐呈稳定持续下坡滚动状态;⑤当斜坡角度与初始角速度满足关系αe<α≤π/n,>dn或π/n <α≤π/2,≥0 时,轮辐会以增速或减速2 种方式趋向且最终等于极限环不动点ω1*,轮辐实现纯被动性质的稳定持续下坡滚动.

表1 不动点与相应吸引盆及斜坡角度的依存关系

图7 轮辐初始条件与运动过程及最终运动状态关系图
4 结论
1)轮辐模型参数一定时,不同的斜坡角度对应不同的庞加莱映射回转图及不动点的存在状态,是轮辐运动极限环存在的重要影响因素.决定极限环不动点存在的临界斜坡角度值依赖于轮辐辐条数目及惯性矩参数.
2)轮辐自身模型参数及所在斜坡角度一定时,静止不动点与极限环不动点的吸引盆区域确定,轮辐初始运动条件所属吸引盆类别直接决定轮辐最终运动状态.
3)临界角速度系列为不动点的吸引盆边界值,由轮辐自身模型参数及斜坡角度决定.历经数次碰撞后,以此系列临界角速度为初始条件开始运动的轮辐将耗时无限长,趋向并停留于不稳定竖直平衡位置,而无法到达静止不动点或极限环不动点.
4)轮辐只在重力作用下发生滚动,无附加驱动力,具有纯被动性质,轮辐自身模型参数、斜坡角度、初始运动条件将决定轮辐运动过程及最终运动状态.
5)轮辐自身模型参数即辐条数目、惯性矩参数与临界斜坡角度、临界角速度值、不动点、不动点的吸引盆相互依赖并相互制约.
无边轮辐辐条数目与惯性矩参数类比对应于简单被动双足行走模型运动过程中双腿间最大角度、腿部与髋关节处质量分布,斜坡角度决定无边轮辐或被动双足行走模型行走过程中重力驱动力.因此,两相邻辐条间角度的表征参数辐条数目、惯性矩参数与斜坡角度是无边轮辐、被动双足行走模型的稳定周期状态的决定性因素.
References)
[1] McGeer T.Passive dynamic walking[J].The International Journal of Robotics Research,1990,9(2):62-82.
[2] McGeer T.Passive dynamic biped catalogue [C]//Proceedings of the Experimental Robotics Ⅱ:the 2nd International Symposium.Toulouse,France,1991,190:463-490.
[3] 毛勇,王家廞,贾培发,等.双足被动步行研究综述[J].机器人,2007,29(3):274-280.Mao Yong,Wang Jiaxin,Jia Peifa,et al.Passive dynamic biped walking:a survey [J].Robot,2007,29(3):274-280.(in Chinese)
[4] Collins S,Ruina A,Tedrake R,et al.Efficient bipedal robots based on passive-dynamic walkers[J].Science,2005,307(5712):1082-1085.
[5] Coleman M J,Chatterjee A,Ruina A.Motions of a rimless spoked wheel:a simple three-dimensional system with impacts[J].Dynamics and Stability of Systems,1997,12(3):139-159.
[6] Coleman M J.A stability study of a three-dimensional passive-dynamic model of human gait [D].Ithaca,NY,USA:Cornell University,1998.
[7] Coleman M J.Dynamics and stability of a rimless spoked wheel:a simple 2D system with impacts[J].Dynamical Systems an International Journal ,2010,25(2):215-238.
[8] Hodgins J K.Bipedal gait transitions [C]//Proceedings of the IEEE International Conference on Robotics and Automation.Sacramento,CA,USA,1991:2092-2097.
[9] Anderson S O,Wisse M,Atkeson C G,et al.Powered bipeds based on passive dynamic principles[C]//Proceedings of the 5th IEEE-RAS International Conference on Humanoid Robots.Tsukuba,Japan,2005:110-116.
[10] Asano F,Kawamoto J.Modeling and analysis of passive viscoelastic-legged rimless wheel that generates measurable period of double-limb support[J].Multibody System Dynamics,2014,31(2):111-126.
[11] Beigzadeh B,Meghdari A,Sohrabpour S.Passive dynamic object manipulation:a framework for passive walking systems[J].Journal of Multi-Body Dynamics,2013,227(2):185-198.
[12] Sabaaapour M R,Hairi-Yazdi M R,Beigzadeh B.Towards passive turning in biped walkers[J].Procedia Technology,2014,12(1):98-104.
[13] Gamus B,Or Y.Dynamic bipedal walking under stick-slip transitions [J].Society for Industrial and Applied Mathematics:Journal of Applied Dynamical Systems,2015,14(2):609-642.
[14] 刘振泽.欠驱动步行机器人运动学机理与控制策略研究[D].长春:吉林大学通信工程学院,2007.
[15] 刘振泽,周长久,田彦涛.Compass-like 无动力双足行走机器人的运动状态[J].吉林大学学报:工学版,2007,37(5):1175-1180.Liu Zhenze,Zhou Changjiu,Tian Yantao.Analysis of compass-like passive biped robot locomotion [J].Journal of Jilin University:Engineering and Technology Edition,2007,37(5):1175-1180.(in Chinese)
[16] 刘丽梅.被动动态行走双足机器人的稳定性分析与控制研究[D].长春:吉林大学通信工程学院,2011.
[17] 胡运富.无膝双足被动机器人的运动特性和稳定性研究[D].哈尔滨:哈尔滨工业大学机电工程学院,2009.
[18] 郭欣.双足被动机器人行走模式的设计构想[D].北京:北京邮电大学自动化学院,2009.
[19] 胡运富,朱延河,吴晓光,等.被动无边轮辐运动特性的Adams 仿真分析[J].哈尔滨工业大学学报,2010,42 (7):1076-1079.Hu Yunfu,Zhu Yanhe,Wu Xiaoguang,et al.Adams simulation analysis of motion characteristic of passive rimless-wheel [J].Journal of Harbin Institute of Technology,2010,42(7):1076-1079.(in Chinese)

