考虑手术间及医疗团队间准备时间的手术排程
朱 悦 张玉林 宋旼珊
(东南大学经济管理学院,南京211189)
医院手术室是高科技设备和专业医护人员最密集的场所.依托手术室进行的医疗服务给医疗机构及社会带来经济和社会效益的同时,产生的成本也很大.杜少甫等[1]发现,手术室产生的费用占医院总费用的40%以上.因此,提高手术室利用率可有效地减少医疗成本.
手术排程中,手术准备时间会影响手术室的利用率.手术准备时间指从上一个病人离开手术室到下一个病人进入手术室的时间.在这段时间内,医疗团队需对手术台进行清理、消毒、更换医疗器材等.此外,2 个不同的医疗团队之间切换也需要准备时间.当相邻手术的类型差异较大时,会更换医疗团队,相应的手术设备变动也较大,带来了额外的准备时间[2].Kodali 等[3]对布里格姆妇科医院手术流程的细分、改进,缩短了手术准备时间,提高了手术室的利用率.Arnaout 等[4]研究了依赖于次序的手术准备时间,以最小化所有手术完成时间为目标,提出LEPST 算法,以提高手术室的利用率.在含有多个手术室的排程问题中,Zhao 等[5]研究了依赖于相邻手术类型的准备时间,采用约束规划,找到使手术室利用率最高的排程.
医疗机构中病人的实际手术时间还受到学习效应影响.学习效应是指随着手术数目的增加,由医生手术经验累积而带来的手术时间缩短[6].学习效应主要体现在手术环节及手术准备环节.Bokhari 等[7]认为,实际手术时间随医生完成的同类手术数增加而递减.Stepaniak 等[8]发现,在腹股沟疝修补手术中,连续进行相类似的手术,可缩短手术准备时间.除此之外,准备时间还存在恶化效应.恶化效应指由于推迟手术带来的实际准备时间增加的现象.Wang 等[9]在考虑准备时间存在恶化效应的加工模型时,认为手术推迟导致的准备时间延长适用于医疗领域,病人病情加重而导致医疗团队需要更长的准备时间.
Wang 等[10]研究了加工时间和准备时间同时存在的恶化效应,当目标函数是完成时间和资源成本的加权和时,在特定参数条件下,该问题可通过多项式算法求解.Lee 等[11]研究了加工时间和准备时间都存在的学习效应,并在组容量相同,准备时间和加工时间存在对应大小关系时,提出解决最小化总完工时间的多项式算法.Yang 等[12]考虑了准备时间和加工时间都具有基于位置和时间两类学习效应的问题,并证明最小化所有工件完工时间能采用多项式算法求解.Kuo[13]进一步研究2 类学习效应,认为基于位置的学习效应适用于准备时间,基于时间的学习效应适用于加工时间,区分了单一学习效应和多个学习效应2 种情形.给出每种情形下,求解最小化所有工件完工时间和总完工时间的多项式算法.
上述工件排程的研究,仅考虑了组与组之间准备时间,没有考虑同组工件加工的准备时间.本文综合考虑手术间和医疗团队间两类准备时间,并考虑手术时间和手术间准备时间存在的学习效应以及医疗团队间准备时间存在的恶化效应,使得所有手术的完成时间最短.
1 问题描述和假设
1.1 问题描述
研究一个工作日内,单一手术室的排程,手术室允许不同医疗团队进行不同类型的手术.考虑同一个医疗团队进行的手术之间的准备时间和不同医疗团队间因调试设备、准备器材需要的准备时间;手术时间和手术间准备时间存在学习效应,医疗团队间准备时间存在恶化效应.需要确定工作日内不同医疗团队进入手术室的次序和医疗团队进行手术的次序,使所有手术完成时间最短.
1.2 假设
本文做如下3 个假设:
1)手术病人数和手术类型术前已知.即所有病人在手术排程前已到达,相应的手术类型确定,不考虑紧急病人到达及已安排手术的病人临时取消手术.
2)医疗团队顺序进场.即某个医疗团队在手术室完成所有手术后,其他医疗团队才可进入手术室工作.
3)确定性环境.即在手术过程中,不考虑手术时间因实际情形的复杂性等而可能带来的额外不可控变化.
假设1 保证手术排程的对象是确定数目的手术病人,排程前可确定参与手术的医疗团队.假设2 依据的是Luo 等[14]有关连续进行同类型手术可以提高手术效率的结论.
2 排程模型及分析
2.1 排程模型
手术排程的目的是提高手术室利用率,指标有多种,如所有手术的完成时间、所有手术完成时间与期望时间的差值之和.Arnaout 等[4]把所有手术的完成时间作为衡量手术室利用率的指标.对给定数目的手术病人,本文将最小化所有手术的完成时间作为目标,研究每个医疗团队进行手术的次序和医疗团队进入手术室的次序,参考Graham 等[15]的一般调度模型表示方法,本文研究的问题可表示为
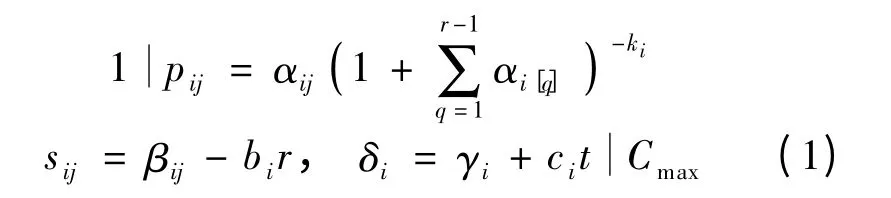
式中,“1”代表单一手术室的排程;pij为病人Jij(编号j)、手术排序为r、由第i 个医疗团队进行手术的时间,j=1,2,…,ni,i=1,2,…,M,ni为医疗团队i的手术数量;αij为基本手术时间;αi[q]为医疗团队i参与的第q(q=1,2,…,ni)台手术的基本手术时间,与手术排程有关;ki为医疗团队i 手术过程中的学习效应常数,满足ki>0;sij为实际术前准备时间,属于手术间准备时间;βij为基本准备时间;bi为医疗团队i 术前准备过程中的学习效应常数,满足bi>0;δi为医疗团队i 实际的医疗团队间准备时间;γi为基本准备时间;ci为医疗团队i 进入手术室后,调试设备、准备器材过程中的恶化效应常数,满足ci>0;t 为医疗团队i 进入手术室的时刻;Cmax为所有手术的完成时间.
2.2 模型分析
引理1 当x≥0,t≥1,λ≥1,k≥0 时,恒有(λ-1)t-k+(t+λx)-k-λ(t+x)-k≥0.
证明过程略.结合引理1,可确定医疗团队进行手术次序的排序.
定理1 对任意医疗团队i,按病人基本手术时间αij的非减序列安排手术,可使其完成所有手术的时间最短.
证明 ①情形1,医疗团队i 只需完成1 台手术.此时,定理1 显然成立.②情形2,医疗团队i需要完成2 台以上手术.反证法证明之.假设存在一个最优的手术排序π1=(S1,Jiu,Jiv,S2)不满足定理1,即存在相邻的2 个病人Jiu和Jiv,满足αiu>αiv.其中,S1和S2分别表示子排序,包含若干病人,也可能是空集.
记排序π1中,病人Jiu第r 个进行手术,其进入手术室的时刻为t.
保持S1和S2中的病人次序不变,交换病人Jiu和Jiv的位置,得到一个新的手术排序π'1=(S1,Jiv,Jiu,S2).在按照排序π1情况下,病人Jiu和Jiv完成手术的时间分别为Ciu(π1)和Civ(π1),可分别表示为
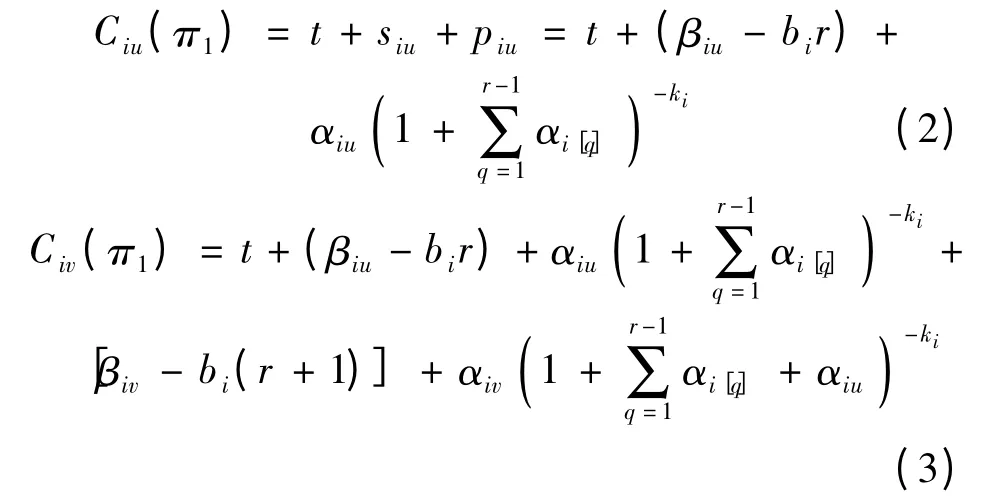
类似地,在按照手术排序π'1情况下,病人Jiu完成手术的时间为
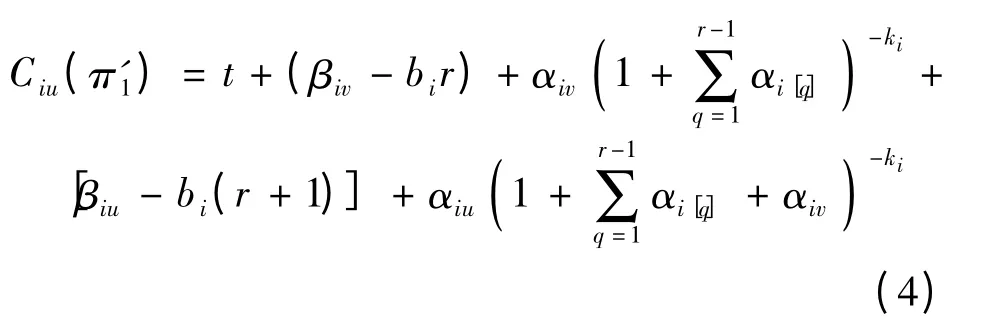
将式(3)和式(4)相减,可以得到
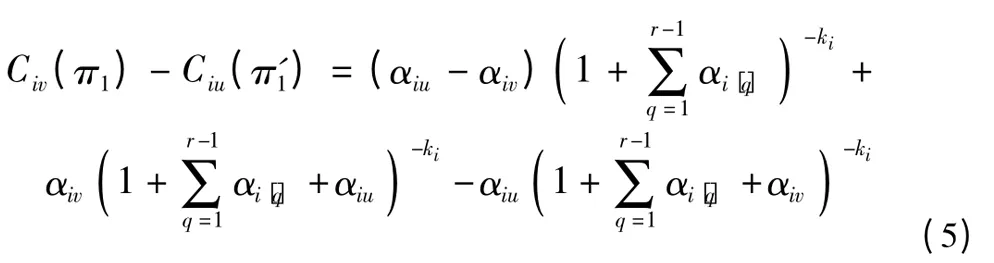
定理1 确定的是不同团队内的手术次序,下述定理2 确定了医疗团队进入手术室的次序.
定理2 医疗团队i(i=1,2,…,M)按照对应ρi值的非减序列依次进入手术室,可使所有手术的完成时间最短,其中
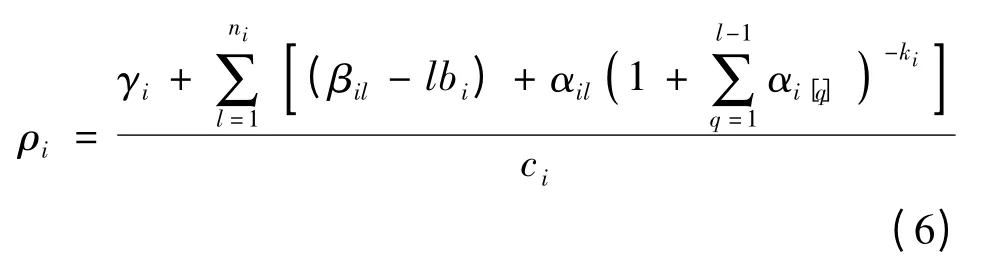
证明 ①情形1,工作日只有1 个医疗团队参与手术.定理2 显然成立.②情形2,至少有2 个医疗团队参与手术.反证法证明之.假设存在一个最优排序π2=(R1,Gi,Gi',R2)不满足定理2(i'=1,2,…,M).Gi和Gi'代表2个相邻的医疗团队,满足ρi>ρi'.其中,R1和R2代表子排序,包含若干医疗团队,也可能是空集.
记R1中最后一个医疗团队完成手术的时刻为t.交换排序π2中,医疗团队Gi和Gi'的位置,得到一个新的排序π'2=(R1,Gi',Gi,R2).
在排序π2下,医疗团队Gi'完成所有手术的时间为
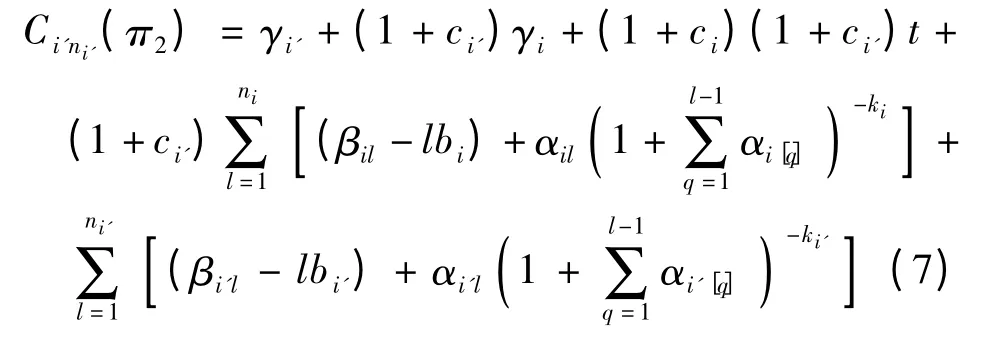
类似地,在排序π'2下,医疗团队Gi完成所有手术的时间
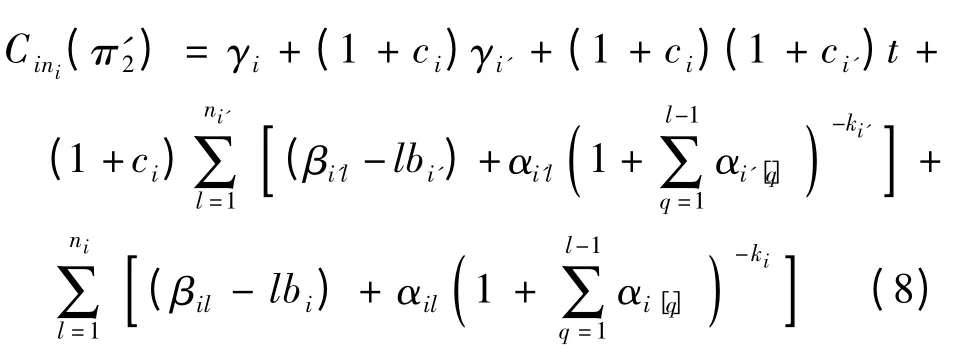
将式(7)和式(8)相减,可以得到
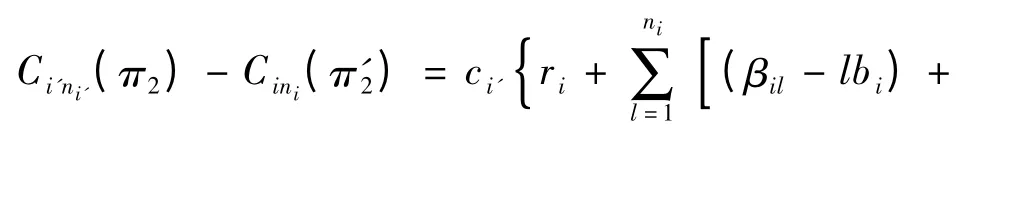
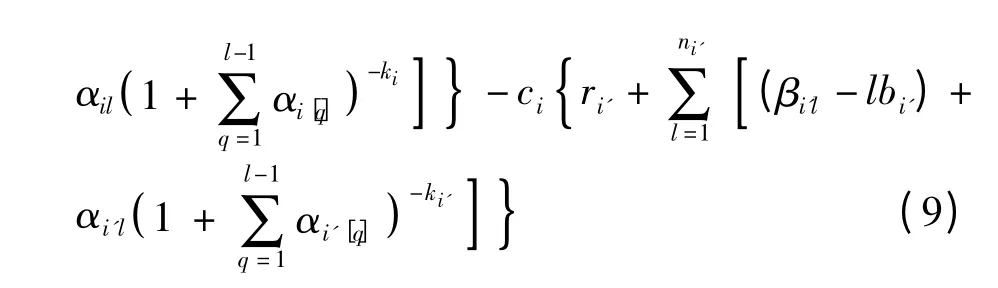
当满足ρi>ρi'时,恒有Ci'ni'(π2)>Cini(π'2).
在手术排序π2和π'2中,子排序R1和R2是相同的.因此按照排序π'2情况下,所有手术的完成时间短于排序π2下所有手术的完成时间.这说明π'2较π2更优,矛盾.故定理2 成立.
定理2 确定了医疗团队进入手术室的次序.按照定理1 和定理2,确定医疗团队进入手术室的次序和医疗团进行手术的次序,可使所有手术的完成时间最短.
2.3 排程算法及分析
根据定理1 和定理2,得到使所有手术完成时间最短的排程算法如下:
①每个医疗团队按病人基本手术时间的非减序列确定手术次序.计算复杂度为
②计算医疗团队i(i=1,2,…,M)的ρi值.计算复杂度为O(M).
③按ρi值的非减序列依次安排相应团队进入手术室.计算复杂度为O(MlogM).
整个算法的计算复杂度为O(nlogn),n=n1+n2+…+nM.
3 算例分析
本文依据第2 节提出的定理及算法,模拟现实手术的排程,确定最优手术排程的过程.相关参数为:某个工作日中,共有10 名病人需安排手术,涉及3 种手术类型,分别由医疗团队1,2,3 负责,对应的病人数分别为3,4,3,手术病人及医疗团队的参数取值如表1所示.
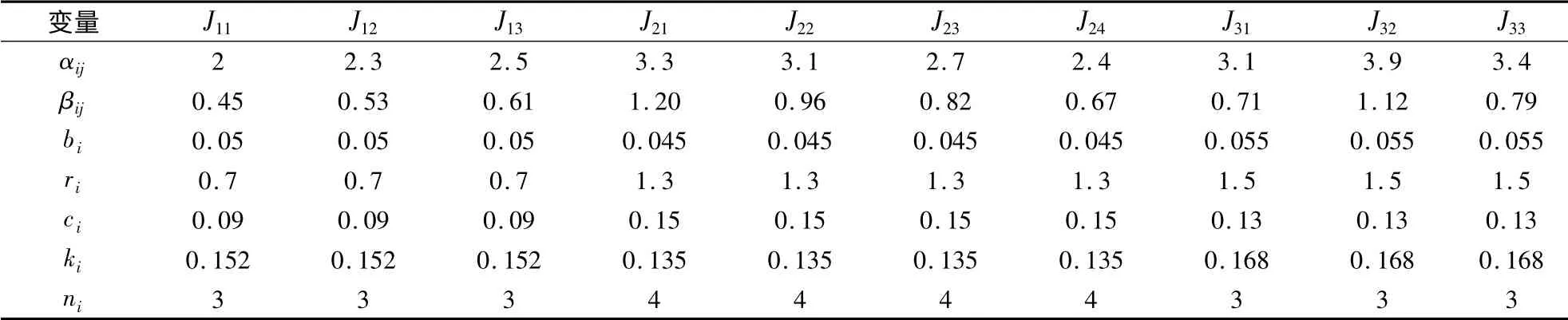
表1 手术病人及医疗团队的参数取值
对医疗团队1,由于α11<α12<α13,故病人J11,J12和J13依次接受手术.类似地,对医疗团队2,病人J24,J23,J22和J21依次接受手术;对医疗团队3,病人J31,J33,J32依次接受手术.计算3 个医疗团队对应的ρi值,即

由于ρ1<ρ2<ρ3,因此医疗团队1,2,3 依次进入手术室.使所有手术完成时间最短的排程为:(J11→J12→J13)→(J24→J23→J22→J21)→(J31→J33→J32),最短时间为38.48.
在该排程下,医疗团队1 首先进入手术室.由于手术没有推迟,因此不存在恶化效应,医疗团队的准备时间为0.7.病人J11,J12和J13依次接受手术,实际手术时间分别为2.00,1.95 和1.94,相比基本手术时间,均明显缩短(除病人J11外),体现医疗团队1 在手术中的学习效应.每位病人的术前准备时间分别为0.40,0.43 和0.46,相比基本术前准备时间,也明显缩短,体现医疗团队1 在术前准备中的学习效应.医疗团队2 第2 个进入手术室,手术被推迟,团队的准备时间延长,实际值为2.48,反映医疗团队间准备时间具有的恶化效应.病人J24,J23,J22和J21依次接受手术,实际手术时间分别为2.40,2.29,2.43 和2.45,相比基本手术时间,均明显缩短(除病人J24外),因为医疗团队2 累积了手术经验.由于医疗团队2 累积了术前准备的经验,实际的术前准备时间分别缩短为0.63,0.73,0.83 和1.02.医疗团队3 最后进入手术室,手术延迟使团队的准备时间延长至4.51.病人J31,J33和J32依次接受手术.由于医疗团队3 在手术和术前准备环节累积的经验,实际手术时间缩短至3.10,2.68 和2.78;实际术前准备时间缩短至0.66,0.68 和0.96.
4 结语
本文构建了包含手术间准备时间和医疗团队间准备时间的排程模型,考虑了手术时间和手术间准备时间存在的学习效应,以及医疗团队间准备时间存在的恶化效应,以最小化所有手术完成时间为目标,确定了每个医疗团队进行手术的次序和医疗团队进入手术室的次序.研究证明:每个医疗团队按病人基本手术时间的非减序列进行手术,按某给定多项式的非减序列依次进入手术室,是最优排程.考虑其他时间约束对手术排程的影响,是今后的研究方向.
References)
[1] 杜少甫,谢金贵,刘作仪.医疗运作管理:新兴研究热点及其进展[J].管理科学学报,2013,16(8):1-19.Du Shaofu,Xie Jingui,Liu Zuoyi.Progress and prospects in an emerging hot topic:healthcare operations management[J].Journal of Management Sciences in China,2013,16(8):1-19.(in Chinese)
[2] Austin T M,Lam H V,Shin N S,et al.Elective change of surgeon during the OR day has an operationally negligible impact on turnover time[J].Journal of Clinical Anesthesia,2014,26(5):343-349.
[3] Kodali B S,Kim D,Bleday R,et al.Successful strategies for the reduction of operating room turnover times in a tertiary care academic medical center[J].Journal of Surgical Research,2014,187(2):403-411.
[4] Arnaout J P M,Kulbashian S.Maximizing the utilization of operating rooms with stochastic times using simulation[C]//Proceedings of the 2008 Winter Simulation Conference.Miami,FL,USA,2008:1617-1623.
[5] Zhao Z X,Li X P.Scheduling elective surgeries with sequence-dependent setup times to multiple operating rooms using constraint programming [J].Operations Research for Health Care,2014,3(3):160-167.
[6] Ziaee S A M,Mohammadi S M,Kashi A H,et al.Evaluation of the learning curve for percutaneous nephrolithotomy[J].Urology Journal,2010,7(4):226-231.
[7] Bokhari M B,Patel C B,Ramos-Valadez D I,et al.Learning curve for robotic-assisted laparoscopic colorectal surgery [J].Surgical Endoscopy,2011,25(3):855-860.
[8] Stepaniak P S,Vrijland W W,de Quelerij M,et al.Working with a fixed operating room team on consecutive similar cases and the effect on case duration and turnover time[J].Archives of Surgery,2010,145(12):1165-1170.
[9] Wang J J,Liu Y J.Single-machine bicriterion group scheduling with deteriorating setup times and job processing times[J].Applied Mathematics and Computation,2014,242:309-314.
[10] Wang D,Huo Y Z,Ji P.Single-machine group scheduling with deteriorating jobs and allotted resource[J].Optimization Letters,2014,8(2):591-605.
[11] Lee W C,Wu C C.A note on single-machine group scheduling problems with position-based learning effect[J].Applied Mathematical Modelling,2009,33(4):2159-2163.
[12] Yang S J,Yang D L.Single-machine scheduling simultaneous with position-based and sum-of-processingtimes-based learning considerations under group technology assumption[J].Applied Mathematical Modelling,2011,35(5):2068-2074.
[13] Kuo W H.Single-machine group scheduling with timedependent learning effect and position-based setup time learning effect [J].Annals of Operations Research,2012,196(1):349-359.
[14] Luo L,Yao D D,Huang X,et al.Sequence-dependent anesthesia-controlled times:a retrospective study in an ophthalmology department of a single-site hospital[J].Anesthesia &Analgesia,2014,119(1):151-162.
[15] Graham R L,Lawler E L,Lenstra J K,et al.Optimization and approximation in deterministic sequencing and scheduling:a survey[J].Annals of Discrete Mathematics,1979,5:287-326.

