城市轨道交通车站客流模态与控制策略

李 曼 王艳辉 贾利民

(北京交通大学轨道交通控制与安全国家重点实验室，北京100044)

(北京交通大学交通运输学院，北京100044)

城市轨道交通具有速度快、频率高、运量大等特点，已成为城市居民出行的主要工具.伴随路网规模的不断扩大和客流负荷量的不断提高，运营安全管理工作难度随之增大.如何从车站各部分设备设施的客流流动关系以及客流状态演变机理两个方面分析车站客流群体行为，对提高城市轨道交通的服务质量和安全管理部门相关工作的开展具有重要意义.

目前国内外学者对城市轨道交通车站客流演化模型已进行了相关研究.薛霏等［1］基于系统动力学理论建立了城市轨道交通车站客流的演变模型及演变算法，综合考虑了列车满载率、闸机通过能力等因素来分析客流演变规律.曹志超［2］提出了无约束的突发大客流演化模型，仿真其在网络中的演化过程，通过调整参数来分析讨论大客流传播速率和消散速率相对变化的关系.骆晨等［3］基于网络拥挤模型建立超大客流拥堵网络疾病传播模型，通过参数反演将SIR 模型的传播特性运用于城市轨道交通网络.Chen 等［4］分析了客流和通过能力之间的关系，给出了密集区域的速度密度曲线，并推演了客流消散模型.Daamen［5］研究了公共交通设施中的客流模型，包括客流行为模型、分配模型等.

在客流行为方面，国内外学者主要进行了以下研究.Zhang 等［6］基于元胞自动机理论建立了以北京地铁车站为背景的上下车客流微观模型，来刻画上下车客流行为.徐瑞华等［7］提出了一种基于多路径选择机制的客流分布模型，并基于深度优先搜索算法确定可行路径.张琦等［8］基于元胞自动机理论对MTR 车站客流进行仿真建模，研究了MTR 车站客流行为特征，刻画了宏观的客流群体行为.Chen 等［9］从宏观上对客流参数之间的关系进行了分析，建立了能够反映速度密度与流量之间关系的交通流模型.

综上所述，宏观客流行为方面的研究主要关注行人空间及设施布局的分配与优化、大客流组织的疏散［10-13］、客流群体行为的特征、客流群体行为的演化等.微观客流行为的研究主要以行人为研究对象，研究有效行为空间中行人个体特性、上下车客流行为、行人流线选择特性等.

关于客流群体行为演化机理的研究，多是应用仿真软件通过调整模型参数来对客流行为进行仿真，但在数学模型的解析求解与解析解的条件分析证明方面，以及模型的理论推导方面研究较少.本文基于系统动力学原理构建了车站客流演化数学模型，用来刻画群体客流行为演化机理.基于系统行为理论给出了城市轨道交通车站客流模态的概念，通过求解车站客流演化模型的解析解和分析模型的稳定性及稳定性条件，得出车站客流系统特定模态集以及各模态对应的物理特征.

1 城市轨道交通车站运营系统客流模态

利用系统动力学理论研究系统内部因素相互作用的演化机理，建立系统动力学行为方程，通过观察不同条件下系统状态的变化特征发现，系统所表现出的现象(行为等)具有可再现性，可用来分析系统行为的发展趋势.这种不同条件下系统状态改变所呈现出的统一特征被称为系统模态［14］，其反映的是相同或相近环境(内部和外部条件)下特定系统行为发生改变时的规律性特征.

定义1 城市轨道交通车站系统客流模态是以车站客流系统为研究对象，在某种环境下其客流状态变化呈现的规律性特征，是一系列系统稳定状态的集合.在一段时间或一个周期内，车站客流行为受到内部和/或外界因素的影响连续地改变，在某一条件的作用下逐步趋于稳定，此时可认为系统达到某一模态;即模态描述了一种特定条件下的系统行为，是系统对此种环境所做出的反应，是系统在不同条件下其内部因素相互作用的结果.

2 模型建立

为建立城市轨道交通车站客流状态演化模型，首先做如下假设:

1)P(t)，Q(t)，R(t)分别表示站厅客流、连接二者的中间设施客流以及站台客流.

2)根据客流时间特征可以将车站运营的时段分为3 类，分别为早高峰、平峰、晚高峰.设同类中单位小时内客流特性是均匀的，各小时的单位时间进站量可用Ai(t)表示，出站量可用hiP(t)表示，其中hi为车站客流出站率.

3)站厅的客流和通往中间设施的客流之间的关系是非线性的，这种非线性由2 个流的相互作用产生，并且与中间设施的拥挤度有关，可用e(t)=aβ(t)P(t)Q(t)来表征.其中，a 为站厅流与中间设施流非线性相互作用关系调节参数;β(t)用来表征中间设施拥挤度对这种相互作用的影响，表示为β(t)=Q(t)/K，K 为中间设施的最大容纳人数.因此，站厅的客流和通往中间设施的客流之间的非线性流动率为aP(t)Q2(t)，0 ＜a ＜1.令e1(t)为站厅客流对中间设施客流的非线性作用关系参数，e2(t)为中间设施客流对站厅客流的非线性作用关系参数.

4)b1与b2分别表示单位时间内中间设施的客流去往站台的客流流动系数和站台去往中间设施的客流流动系数，0 ＜b1，b2＜1.

5)c1与c2分别表示单位时间内站台上车客流比率和下车客流比率，0 ＜c1，c2＜1.

基于以上假设，该模型的框图如图1所示.建立如下客流演化模型:

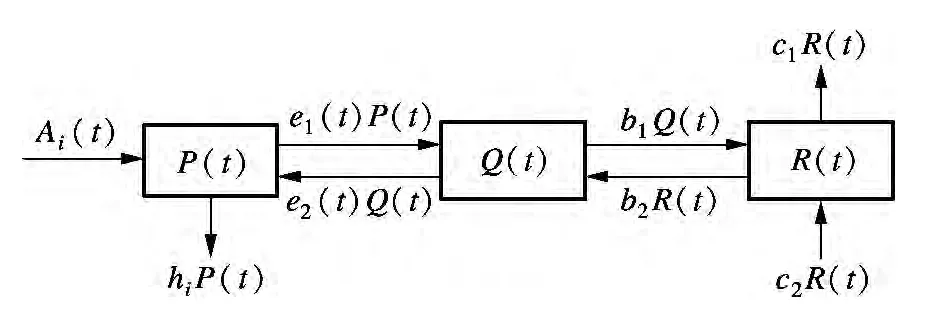
图1 车站内部客流相互作用模型

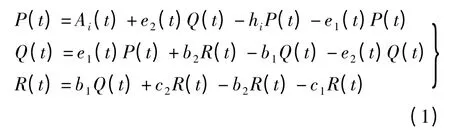
令Δa=a1－a2，Δc=c1－c2，则方程(1)可转化为如下积分形式:

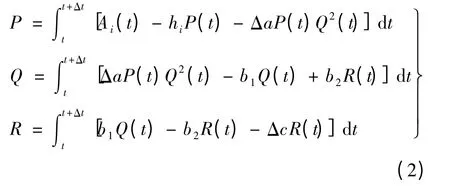
式中，Δa，Δc 满足－1 ＜Δa ＜1，－1 ＜Δc ＜1.

3 基于模型稳定性的车站客流模态集构建

3.1 模型稳态解的存在性与条件分析

下面讨论其他稳态点的存在性.令方程(1)右端为零，同时令方程变形为P(A －函数易得:当Δa ＜0 时，A2－系统有稳态点(P1，Q1，R1);当Δa ＞0 且时，有2 个正稳态点(P2，Q2，R2)和(P3，Q3，R3).

证明 根据系统(1)的微分方程组，可得该系统的雅克比矩阵J 为

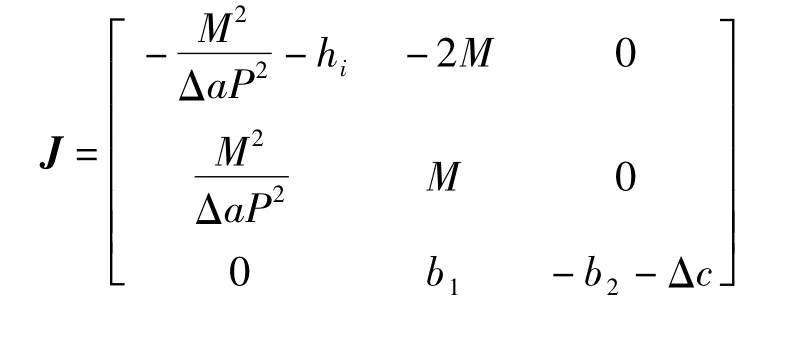
系统在正稳态点处共3 个特征根，分别为r1，r2，r3.将代入特征方程化简，可得

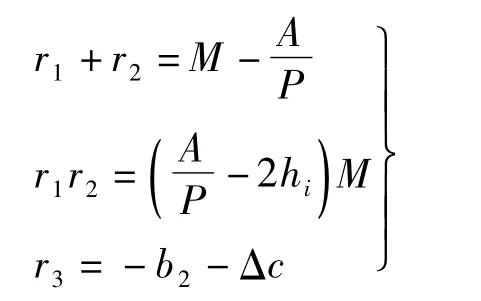
依据雅克比矩阵的性质可知，当雅克比矩阵的特征根均为负根时，可以判定该系统在稳态点处局部渐进稳定［15］.故b2+Δc ＞0 是系统稳定的前提条件.

1)当Δa ＜0，A≤A0，Δc ＜0 时，车站客流系统局部渐进稳定，稳态解为(P1，Q1，R1).当b2+Δc＞0，Δc ＜0 时，则对于点P1，有r1r2＞0，且r1+r2＜0，因此系统在点P1处的雅克比矩阵有3 个负的特征根，此时系统局部渐进稳定.

2)当Δa ＞0，A ＞A0，0 ＜Δc ＜Δc0时，车站客流系统局部渐进稳定，稳态解为(P2，Q2，R2).当0＜Δc ＜Δc0，即0 ＜M ＜2d 时，令显然r1+因r1，r2同号，则r1，r2均小于0，即系统在点P2处的雅克比矩阵共有3 个负的特征根，此时系统渐进稳定.

3)当Δa ＞0，A ＞A0，Δc≥Δc0时，车站客流系统局部渐进稳定，稳态解为(P3，Q3，R3).当Δc≥Δc0，即M≥2hi时，显然令函数因f(P3)=0，且f(P)在区间单调递减，因此当A ＞A0时，有f(P0)＜0，同时P0点在P3点右侧，则有＜0.同上，此时系统在平衡点P3处渐进稳定.

3.2 模态集建立

由第1 节可知，模态是系统一系列稳定状态的集合，描述了一定条件下的系统行为.t0时刻，系统在某一触发条件下开始演化，在t0+iΔt 时刻达到局部渐进稳定状态，此后t0+nΔt 时刻系统行为特征保持稳定.当在另一触发条件下系统参数发生改变，并且满足模态跃迁阈值时，系统由当前模态向另一模态演化，实现模态间的跃迁.

城市轨道交通车站系统的关键变量(进站量、上下车比例、通道拥挤度等)相互作用，在不同时段，影响车站系统客流行为的参数值不同，导致车站客流行为趋于不同的模态，同时不同的系统模态也反映了该条件下的系统行为.3 种模态的物理意义如表1所示.

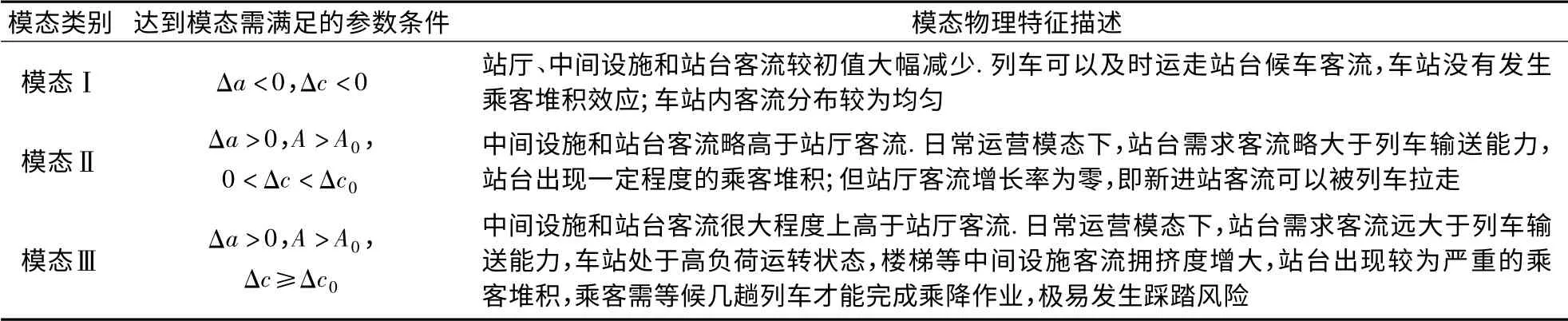
表1 客流状态模态集的建立

4 数值仿真模拟

选取北京某典型地铁站为例，根据某工作日的进出站客流量以及满载率的变化情况，使用Matlab软件，对模型求解并进行数值模拟.

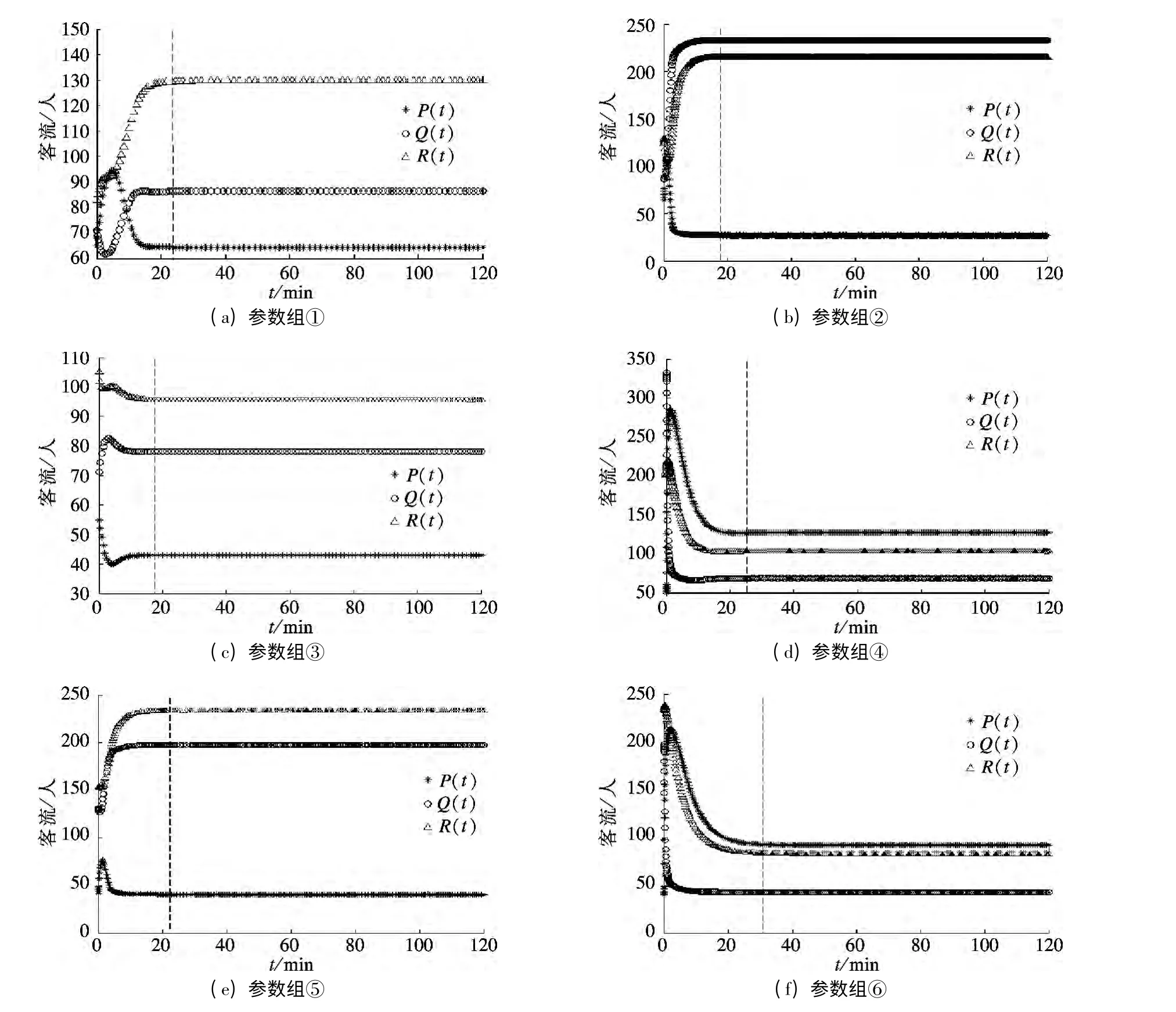
图2 不同参数组下的客流模态

图2(a)和(c)显示了当A ＞A0，0 ＜Δc ＜Δc0时系统的动力学轨迹(参数组取表2中的①和③)，描述了客流处于模态Ⅱ的状态.显然，中间设施和站台客流略高于站厅客流.因站台需求客流略大于列车输送能力，站台出现一定程度的乘客堆积.

通过增大A 和Δc 的参数值，使系统满足条件A ＞A0，Δc ≥Δc0，此时系统的动力学轨迹如图2(b)和(e)所示(参数组取表2中的②和⑤).该模拟结果描述了客流处于模态Ⅲ的状态，即站台出现较为严重的乘客堆积，车站处于高负荷运转状态.站厅客流在短时间内达到一个高峰值后慢慢减少，最后趋于稳定.而对于中间设施和站台客流，随着时间的迁移，客流量逐渐增大，最终使得站台需求客流远大于列车输送能力，乘客需等候几趟列车才能完成乘降作业.

表2 数值模拟参数的确定与不同参数下的系统模态

图2(d)和(f)显示了系统处于模态Ⅰ时的动力学轨迹(参数组取表2中的④和⑥)，就整体而言，客流分布较为均匀，没有发生乘客堆积效应.由Δa ＜0 可知，由通道去往站厅的客流流动系数较大，出站客流相对较多，故站厅客流值略高于站台和通道的客流;Δc ＜0 说明列车可以及时运走站台候车客流，车站没有发生乘客堆积效应，即站台需求客流小于列车运输能力.

5 高模态车站客流控制策略

1)减小Δc.模态Ⅲ的客流主要流向为站厅到站台，高峰时段站台客流密度大.通过减小Δc(c1=0.45，0.55，0.65)，即减小列车的发车间隔提高运力，可实现高模态向中模态的跃迁，从而达到减小站台客流密度的目的，如图3所示.

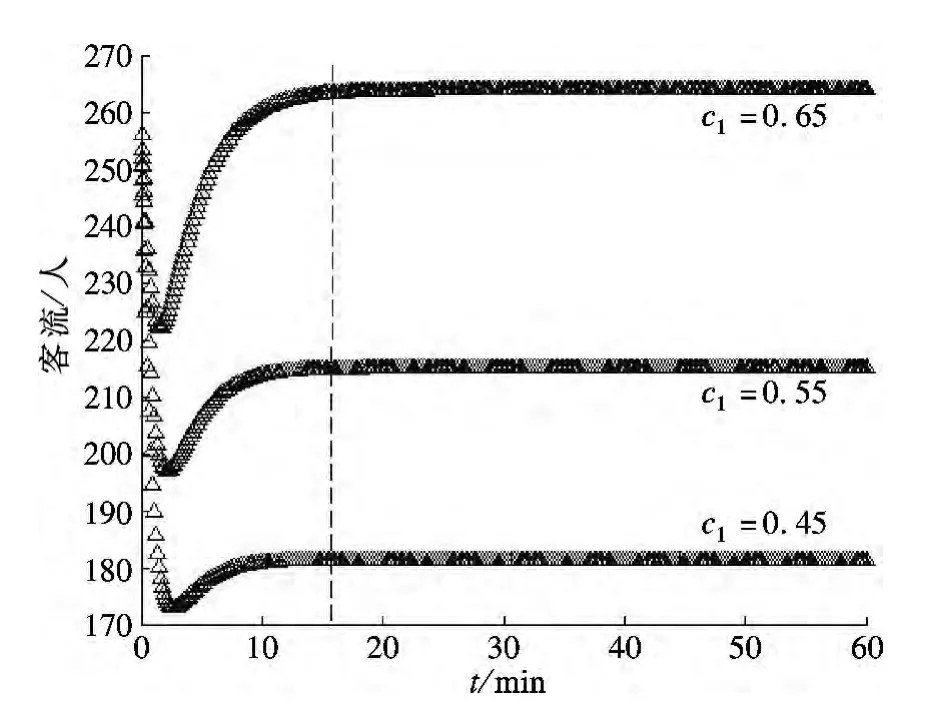
图3 不同上车流动系数下的站台客流R(t)模态

2)减小A.通过对高峰进站客流进行站外限流来减小A，如图4所示.由图可见，在不改变其他参数值的情况下，进行站外限流时，不同进站客流A(A=65，95，125)得到了不同的系统模态平衡点，显然控制进站客流对站台客流拥挤起到了一定的缓解作用，能在一定程度上达到降低站台安全隐患的效果.

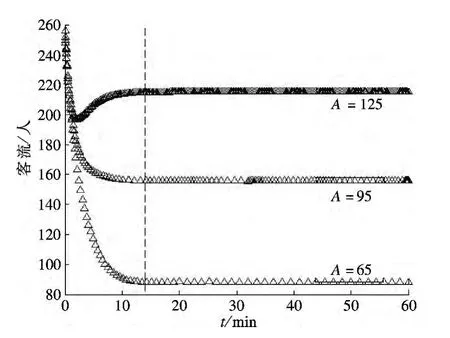
图4 不同进站客流作用下的站台客流R(t)模态

通过以上的参数调整和分析可知，在针对高模态的客流组织和应对措施中，运营公司可以通过站外限流降低单位时间内进站客流人数，缩小发车间隔提高列车运力，以及维护站台排队秩序、实时信息广播等降低站台客流密度，保障车站与乘客的安全.

6 结语

基于系统动力学建模理论，通过对城市轨道交通车站系统的整体与局部的分析，研究车站内部的客流相互作用机制及影响因素，选取关键变量建立城市轨道交通车站内客流演化模型，求解并分析3个模态的物理特征，以及模态转移的阈值条件.通过分析模态转移阈值条件以及数值仿真，得到了高峰时段车站客流控制策略，包括站外限流以及缩小发车间隔等.当进站量值超过阈值A0，且上下车客流差大于Δc0时，车站客流朝模态Ⅲ趋势发展，进入高负荷运营，此时应重点关注.下一步需要深入分析车站客流几种模态之间的转移规律，分析路网与各个车站子系统的联系，从而建立城市轨道交通整个路网客流状态的模态集.

References)

［1］ 薛霏，方卫宁，郭北苑.基于系统动力学的轨道交通车站客流演变算法［J］.铁道学报，2014，36(2):1-10.Xue Fei，Fang Weining，Guo Beiyuan.Rail transit station passenger flow evolution algorithm based on system dynamics［J］.Journal of the China Railway Society，2014，36(2):1-10.(in Chinese)

［2］ 曹志超.网络条件下城市轨道交通突发大客流演化机理和应急策略研究［D］.北京:北京交通大学交通运输学院，2013.

［3］ 骆晨，刘澜，牛龙飞.城市轨道交通超大客流网络拥挤传播研究［J］.石家庄铁道大学学报:自然科学版，2014，27(2):83-86.Luo Chen，Liu Lan，Niu Longfei.Research on urban rail transit large passengers flow network congestion and spread［J］.Journal of Shijiazhuang Tiedao University:Natural Science，2014，27(2):83-86.(in Chinese)

［4］ Chen F，Wu Q B，Zhang H H.Relationship analysis on station capacity and passenger flow:a case of Beijing subway line 1［J］.Journal of Transportation Systems Engineering and Information Technology，2009，9(2):93-98.

［5］ Daamen W.Modeling passenger flows in public transport facilities［M］.Delft，the Netherlands:DUP Science，2004.

［6］ Zhang Q，Han B M，Li D W.Modeling and simulation of passenger alighting and boarding movement in Beijing metro stations［J］.Transportation Research Part C:Emerging Technologies，2008，16(5):635-649.

［7］ 徐瑞华，罗钦，高鹏.基于多路径的城市轨道交通网络客流分布模型及算法研究［J］.铁道学报，2009，31(2):110-114.Xu Ruihua，Luo Qin，Gao Peng.Passenger flow distribution rail transit network model and algorithm for urban based on multi-route choice［J］.Journal of the China Railway Society，2009，31(2):110-114.(in Chinese)

［8］ 张琦，韩宝明，李得伟.地铁枢纽站台的乘客行为仿真模型［J］.系统仿真学报，2007，19(22):5120-5124.Zhang Qi，Han Baoming，Li Dewei.Modeling and simulation of passenger behavior in platform of MTR stations［J］.Journal of System Simulation，2007，19(22):5120-5124.(in Chinese)

［9］ Chen X H，Ye J H，Jian N J.Relationships and characteristics of pedestrian traffic flow in confined passageways［J］.Transportation Research Record，2010，2198:32-40.

［10］ 胡明伟，史其信.城市轨道交通车站客流组织的仿真和评价［J］.交通信息与安全，2009，27(3):39-42.Hu Mingwei，Shi Qixin.Simulation and evaluation of passenger flow organization in urban rail transit station ［J］.Journal of Transport Information and Safety，2009，27(3 ):39-42.(in Chinese)

［11］ Ma J，Lo S M，Chen J，et al.Network based passenger flow modeling for station crowdedness evaluation［J］.Applied Mechanics and Materials，2014，444:986-990 .

［12］ Shi C L，Zhong M H，Nong X Z.Modeling and safety strategy of passenger evacuation in a metro station in China［J］.Safety Science，2012，50(5):1319-1332.

［13］ 张正，蒋熙，贺英松.城市轨道交通高峰时段车站协同限流安全控制研究［J］.中国安全生产科学技术，

2013，9(10 ):5-9.Zhang Zheng，Jiang Xi，He Yingsong.Study on collaborative flow-limiting safety control of urban railway station in peak hours［J］.Journal of Safety Science and Technology，2013，9(10):5-9.(in Chinese)

［14］ 张尊栋.城市道路交通网络多模态动态性建模研究［D］.北京:北京交通大学交通运输学院，2010.

［15］ 周义仓，靳祯，秦军林.常微分方程及其应用［M］.2版.北京:科学出版社，2010:220-235.