直线与圆位置关系问题的解题技巧
王增荣


【摘要】判断直线与圆的位置关系方法纷繁复杂,主要的有“几何法”“代数法”“分类讨论法”等,这些方法适合于不同的题目图形,具体的模型和方法选择需要结合直线与圆位置关系,找到问题的关键所在.本文着重分析高中数学中直线与圆位置关系问题的解题技巧和常用方法,结合实例具体探究.
【关键词】直线与圆;高中数学;解题技巧
“直接与圆位置关系”是一个涉及几何学的重要概念,主要探讨了点、线和圆之间的相互作用,在几何学中,我们常常需要研究点与圆的距离、线与圆的相交情况以及圆在平面上的位置关系.这种关系不仅在数学中具有重要意义,而且在实际应用中也具有广泛的应用,通过深入研究直线与圆位置关系,我们可以更好地理解和解决与圆相关的问题,并为解决实际应用中的难题提供有效的方法和工具.
1 解题技巧1——几何法
“几何法”是处理直线与圆的位置关系的重要方法,在条件复杂、问题情境不明确的直线与圆的题目中,“几何法”的运用给解题带来了明确的位置和数量关系,“几何法”可以帮助我们确定直线与圆的相对位置.如,通过判断直线是否与圆相交,我们可以确定它们的关系是相离、相切还是相交.“几何法”的基本原理可以帮助我们理解直线和圆的交点情况,从而解决相关问题.
通常情况下,运用“几何法”分成三个步骤:第一步,计算圆心到直线的距离d;第二步,比较距离d和半径r的关系;第三步,结合基础知识,得出结论,从而正确解题.
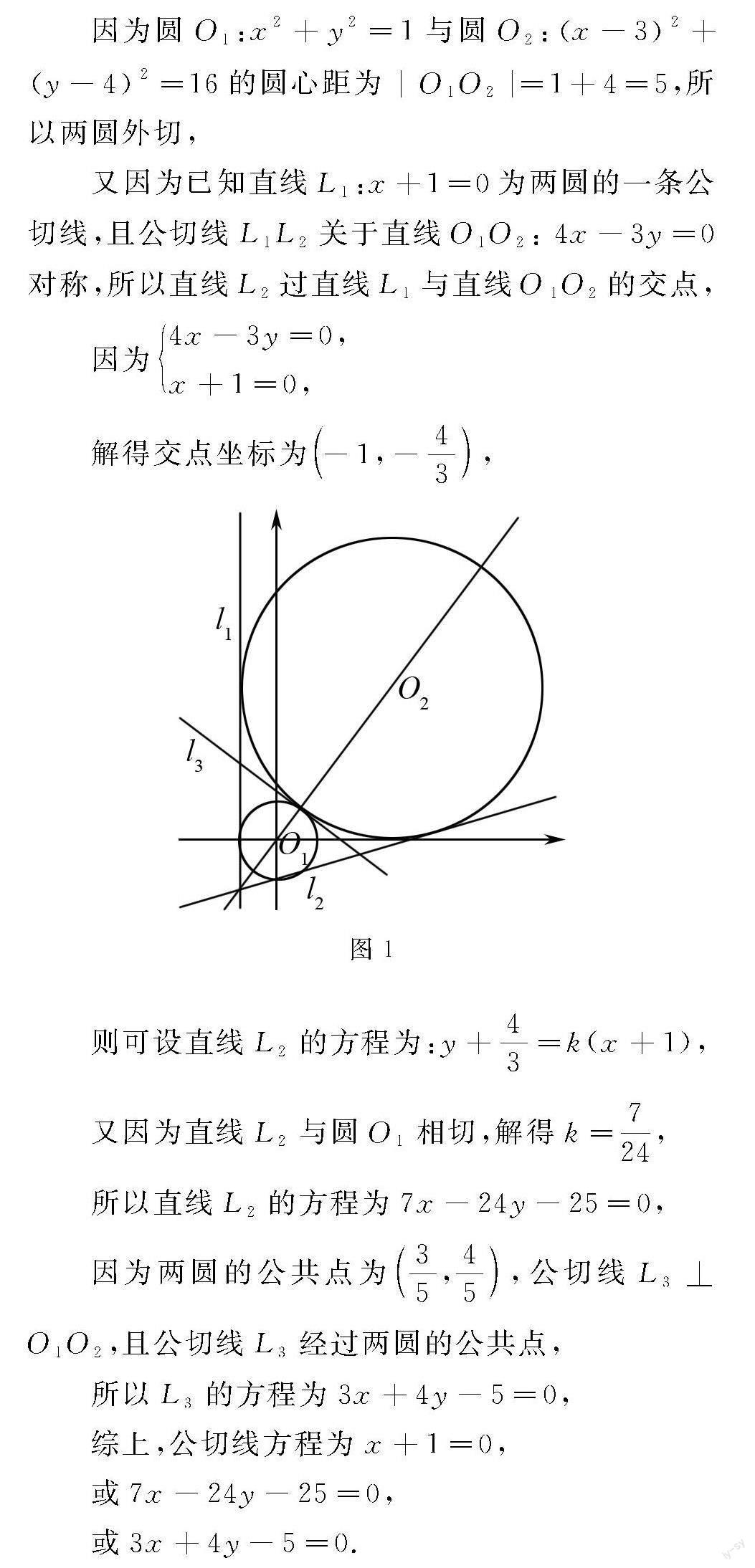
例1 如图1所示,请写出一条与圆x2+y2=1和圆(x-3)2+(y-4)2=16都相切的直线方程.
解法1 求解直线与圆的位置关系,可以借助图形来推导,“几何法”的优势在图形构造中显而易见,可以很好地辅助解题.
因为圆O1:x2+y2=1与圆O2:x-32+y-42=16的圆心距为 | O1O2 |=1+4=5,所以两圆外切,
又因为已知直线L1:x+1=0为两圆的一条公切线,且公切线L1L2关于直线O1O2: 4x-3y=0对称,所以直线L2过直线L1与直线O1O2的交点,
因为4x-3y=0,x+1=0,
解得交点坐标为-1,-43,
图1
则可设直线L2的方程为:y+43=k(x+1),
又因为直线L2与圆O1相切,解得k=724,
所以直线L2的方程为7x-24y-25=0,
因为两圆的公共点为35,45,公切线L3⊥O1O2,且公切线L3经过两圆的公共点,
所以L3的方程为3x+4y-5=0,
综上,公切线方程为x+1=0,
或7x-24y-25=0,
或3x+4y-5=0.
评析 上述求直线与圆位置关系时,借助了圆的几何性质,通过数形结合的方式,运用“几何法”,从而找到了问题的突破口,解决了相切关系下的方程问题.
2 解题技巧2——代数法
在直线与圆的位置关系解题中,“代数法”起着非常重要的作用,“代数法”是指利用代数方法和方程来描述和解决问题的方法,能够提供一种精确的描述,并通过引入变量和方程,我们可以准确地描述直线和圆的性质及位置关系.如,我们可以用方程表示直线的斜率和截距,用方程表示圆的半径和圆心坐标,从而准确地描述它们的位置和关系.通过代数方法,我们可以将问题转化为方程求解的问题,通过求解方程组或方程,我们可以得到直线与圆的交点坐标、交点个数等信息,从而得出准确的结论.同时,“代数法”在直线和圆的位置关系中具有普适性,可以借助题目中的数值条件和位置关系,联立方程组,通过不断解方程组的方式,得到新的数据条件,它为我们解决直线与圆的位置关系问题提供了一种有效的数学工具和方法.仍以例1为例.
解法2 由题意可知,
圆O1:x2+y2=1,
圆O2:(x-3)2+(y-4)2=16,
因此,两圆的公切斜率均不为0,则可设公切方程为x=my+t(m≠0),
所以 | t | = | 3-4m-t | 4,
所以3-4m-t=±4t,
即t2=1+m2,
解得m=0,t=-1,
或m=247,t=257,
或m=-43,t=53.
综上可得,圆的公切方程为:x+1=0,
或7x-24y-25=0,
或3x+4y-5=0.
评析 上述方法是正面解题的写照,从直线与圆的位置关系的问题入手,根据斜率状况,直接设切线方程的公式,并利用“代数法”的特质,计算得出了公切线的数据,从而逐个击破,解决了直线与圆位置关系的相关问题.
3 解题技巧3——分类讨论法
在直线与圆的位置关系解题中,分类讨论起着非常重要的作用,通过分类讨论,我们可以将复杂的问题简化为更容易处理的几个子问题,从而更好地理解和解决整个问题.以下是直线与圆的位置关系中常见的几种情况:直线与圆相离,这种情况下,直线与圆没有交点,我们可以通过计算直线到圆心的距离与圆的半径的关系来判断直线与圆是否相离.直线与圆相切,这种情况下,直线与圆仅有一个交点,这个交点是圆上的点,我们可以通过计算直线到圆心的距离与圆的半径的关系来判断直线与圆是否相切.直线穿过圆,这种情况下,直线与圆有两个交点,直线穿过圆的内部,我们可以通过计算直线与圆的方程来求解交点的坐标.
例2 试着就m的值讨论直线:x-my+4=0与圆x2+y2=4的关系.
解 由方程组x-my+4=0,x2+y2=4,
消去x可得, 1+m2y2-8my+12=0,
Δ=-8m2-41+m2×12=16m2-48,
根据m的取值范围,可以分类得:
当Δ<0时,此时直线与圆相离;
当Δ>0时,此时直线与圆相交;
当Δ=0时,此时直线与圆相切;
评析 通过对直线与圆位置關系的情况的分类讨论,我们可以根据具体情况选择合适的方法和策略来解决问题,在这道例题中,有关Δ的分类讨论可以帮助我们更好地理解直线与圆的位置关系,并能够更高效地解决相关问题.
4 结语
通过学习直线与圆的位置关系技巧,我们可以更好地理解和解决几何问题,包括直线与圆的交点、切点和相切关系等概念都可以帮助我们推导出更多有用的结论.在实际应用中,直线与圆的位置关系问题还可以用“待定系数法”“切线长定理”等方法解决,掌握这些技巧不仅能提高我们的问题解决能力,还可以培养我们的逻辑思维和创造力.因此,深入理解直线与圆的位置关系技巧对于我们的学习和成长都具有重要意义.

