排列、组合在实际问题中的应用探究
韦天君


【摘要】排列、组合问题是中职数学数理统计的重点知识,问题种类多,数量关系复杂,稍不注意就容易出错,因此熟练掌握排列、组合的运用是学好数理统计的基础.本文将排列、组合的知识分而论之,分析核心知识点,归纳解题方法,以期望帮助学生对排列、组合问题有更全面的了解.
【关键词】排列;组合;高中数学;解题技巧
1 排列问题的应用
中职数学的排列问题通常是常见策略针对问题,或者有限制条件的排列问题.常与分类计数原理和分步计数原理综合运用,一般事件对应的方法种数不多,多以选择题或填空题的形式出现,有时也作为求分布列或概率的步骤之一,在解答这类问题的时候注意分类与分步区别,运用正确的策略[1].
1.1 方法提炼
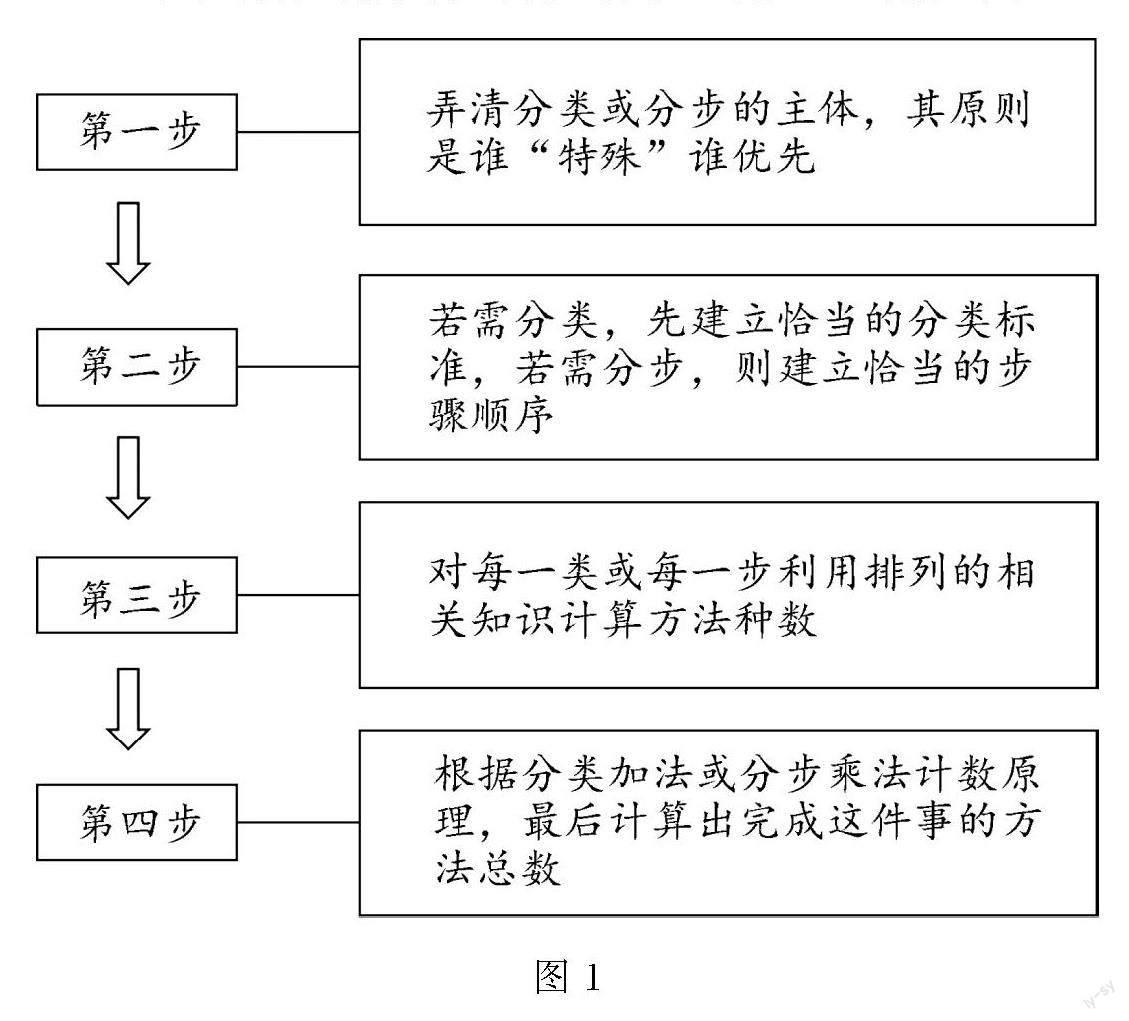
对于有限制条件的排列问题,解题思路如图1.
图1
1.2 实例讲解
例1 设有6个数字,分别为0,1,2,3,4,5,将其随机组成五位数,要求这个五位数中没有重复的数字,求其组成的数字中大于40000的偶数共有多少个?
分析 特殊情况优先安排,若问题中出现特殊“情况”,比如某些不同元素,或某些不同位置,则优先进行处理,然后排列非特殊的元素或位置.在本题所给的6个数字中,第一个特殊情况是要求比40000大,因此只能以4或5开头;第二个特殊情况是限制条件“偶数”,决定了组成的数字末位只能为0,2,4.以此展开分析,问题便会迎刃而解.
解 数字0,1,2,3,4,5中仅有0,2,4三个偶数,比40000大的偶数为以4开头与以5开头的数.
其中以4开头的偶数又分以0结尾与以2结尾,有2A34=48个;同理,以5开头的有3A34=72个.
因此共有48+72=120个.
2 组合问题的应用
中职数学的组合问题多以列举生活实例进行考查,多为选择题和填空题,有时作为求分布列、期望、方差的解答题中的步骤之一,要求学生熟练掌握基本概念与运算方法[2].
2.1 方法提炼
(1)解决组合问题的几种常见方法:正难则反、树形图和分类讨论.
(2)组合问题的限制条件,主要是取出的元素中“含”或“不含”某些元素,在解答时可用以下两种方法:
①=1\*GB3\*MERGEFORMAT直接法:分析清楚组合方式,直接列算式进行计算;
②=2\*GB3\*MERGEFORMAT间接法:从正向进行分析,组合方法多而杂的时候,如“至多”或“至少”类问题,则从问题的逆向进行分析,求出易计算的反面组合方法,用总的方法数减去反面组合方法数,即可得到题目要求的正面组合方法数.
(3)分组问题,有关分组的问题有不平均分组、平均分组两种情况:
①=1\*GB3\*MERGEFORMAT非均匀不编号分组:n个不同元素分成m组,每组元素数目均不相同,且不考虑各组间的顺序,不管是否分尽,分法种数为A=Cm1nCm2n-m1Cm3n-m1-m2…Cmmn-m1-m2-…-mm-1(其中m1,m2……mm中任何两个元素都不相等);
②=2\*GB3\*MERGEFORMAT均匀不编号分组:将n个不同元素均匀分成m组,不管是否分尽,其分法种数为AAmm(其中A=Cm1nCm2n-m1Cm3n-m1-m2…Cmmn-m1-m2-…-mm-1)[3].
2.2 实例讲解
例2 6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有多少种?
解 第一步,安排甲场馆的志愿者,则甲场馆的安排方法有C16=6种;
第二步,安排乙场馆的志愿者,则乙场馆的安排方法有C25=10种;
第三步,安排丙场馆的志愿者,则丙场馆的安排方法有C33=1种.
所以共有6×10×1=60种不同的安排方法.
例3 高三(1)班和(2)班分别有2个同学和4个同学获得科技比赛的参赛资格,但是最终只能选3个人参加,且高三(1)班至少有1个同学入选,请问共有多少种不同的选法.
解 从全部6位同学中选3人共有C36=20种选法,而其中选出的3人都是高三(2)班的选法有C34=4种,所以至少有1位高三(1)班同学入选的选法有20-4=16种.
3 排列、组合综合问题
排列、组合的综合问题是中职数理统计的重点,多以选择题、填空题的形式对学生进行考查,难度不大,多为中档题.
3.1 方法提炼
解排列、组合综合问题要从“分析”“分类”“分步”的角度入手,如图2.
图2
3.2 实例讲解
例4 4个大学生想要向公众宣传环保知识,现选定3个居民小区进行宣传,为了提高效率,它们决定分头行动,每个学生挑1个小区进行宣传,每个小区至少要有1个学生去,请问共有多少种不同的安排方法?
解 因为每个小区至少安排1名同学,所以4名同学的分组方案只能为1,1,2.
所以不同的安排方法共有
C14·C13·C22A22·A33=36种.
例5 现有两组数字,分别为“1,3,5,7,9”和“0,2,4,6”,从每组数字中任意取出2个数字组成四位数,要求这个四位数没有重复数字,请问共有多少种组合方法?
解 含有数字0的没有重复数字的四位数共有C25·C13·A13·A33=540个;
不含数字0的没有重复数字的四位数共有C25·C23·A44=720个,
因此一共可以组成540+720=1260个没有重复数字的四位数.
參考文献:
[1]刘世森.高中生排列组合学习障碍的干预研究[D].济南:山东师范大学,2022.
[2]张若琦.高考中排列组合问题的解法归类研究[J].数学学习与研究,2021(36):150-152.
[3]杨卫.高中数学课堂排列组合教学研究[J].数理天地(高中版),2022(22):4-5.

