立足“一以贯之” 实现“数学相通”——以“多边形的内角和、外角和的证明”为例

⦿ 江苏省南京市将军山中学 张 俊

1 引言

对于多边形内角和、外角和的内容,笔者一直颇有兴致,尤其是相关结论的证明更需“一以贯之”.于是笔者尝试将相关结论的证明过程进行有机整合,达到证明方式与思考路径的“一以贯之”,让学生对本部分内容进行内化并追本溯源,全面审视所学知识,提高立足点,关注知识的形成过程,达到将知识融会贯通的目的,让学生在知识、思想与方法上实现“一以贯之”[1].

2 教学过程设计

问题1如何证明“三角形内角和是180°”?

追问1:问题1的这些证明方法,有什么共同点?

追问2:拼接点除了顶点处,还可以在哪里?

设计意图：帮助学生回忆三角形内角和的证明本质,即借助平行线将三个内角拼成平角或同旁内角(如图1～3).而构成平角的拼接点可以在顶点处,也可以在边上、内部或外部(如图4～6)[2].

图1

图2

图3

图4

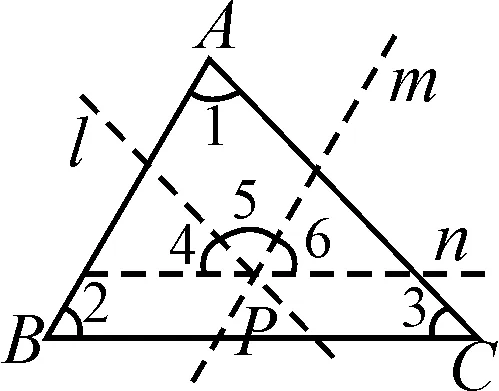
图5

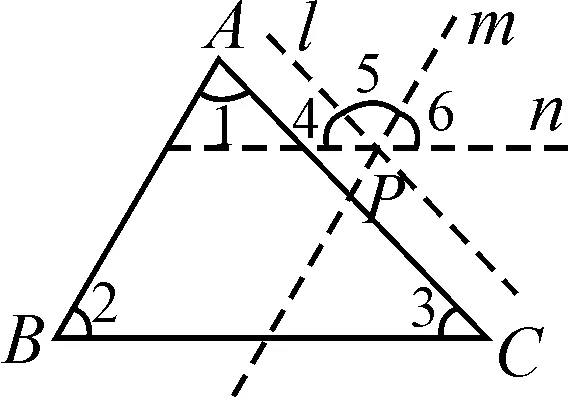
图6

问题2关于点的位置的选择问题,你有过类似的经验吗?

追问1:如何得到多边形的内角和公式?

追问2:你有什么猜测?

设计意图：借由此问,帮助学生明确多边形内角和定理证明的本质,就是把多边形变成若干个三角形.而分割线可以过顶点,也可以过边上、内部、外部的任意一点进行分割(如图7～10).通过追问,引发学生对多种方法证明外角和定理的思考.

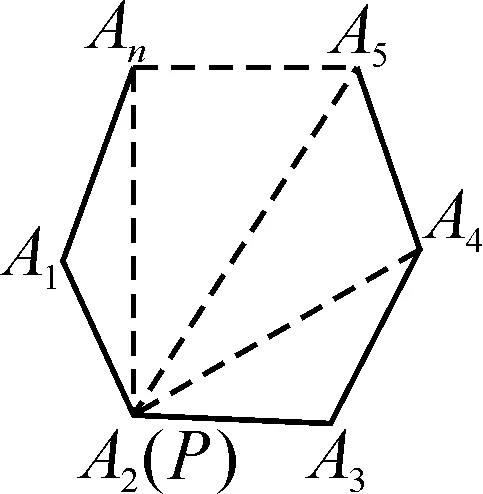
图7

图8

图10

问题3根据已有经验,对于证明“三角形的外角和是360°”,你准备如何开展研究?

设计意图：帮助学生根据已有经验,从周角入手,明确三角形外角和的证明其本质就是把外角拼接到一起转化为一个周角.因此,构造周角的点P既可以置于三角形的顶点处,也可以置于三角形的边上、内部和外部.(如图11～14)

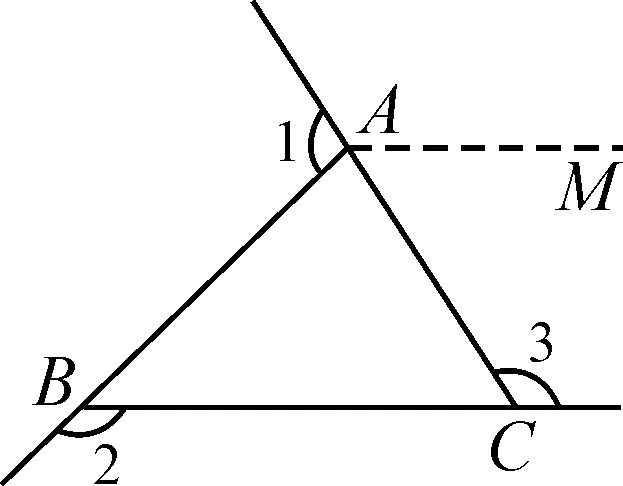
图11

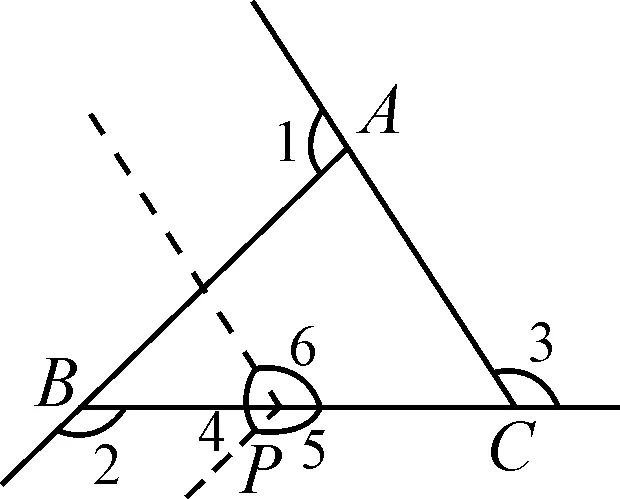
图12

图13

图14

追问1:接下来你准备如何继续开展研究?

追问2:如何证明“多边形的外角和为360°”?

设计意图：类比之前的学习,学生可以熟练地利用平行线,将各外角进行平移、拼接.而拼接点的位置自然可以在顶点、边上、内部、外部等位置.

问题4通过对内角和与外角和结论证明方法的梳理,你有哪些感受?

设计意图：在梳理中,让学生感觉到证明方法虽然多样,但关键都是如何平移角的问题.方法虽然很丰富,但平移角的时候,辅助线都不太好添加.

追问:为了让证明更具简洁美,可以从复杂图形中寻找出简洁的基本图形,请试着找一找.

设计意图：帮助学生找到这个不变的基本图形,可称为“移动的平角”.同样地,在三角形的外角和证明过程中,也存在这样一个不变的图形,那就是“移动的周角”.(如图15～16)

图15

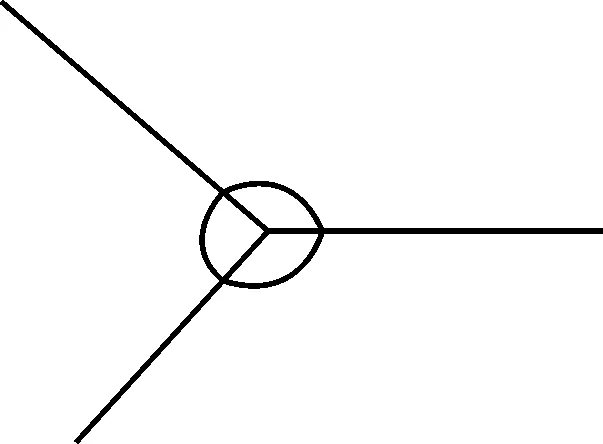
图16

问题5能否设计一个转笔游戏,来验证内角和与外角和的大小呢?

设计意图：设计转笔游戏,可让学生结合转动的位置判断属于内角和(如图17)还是外角和(如图18),再根据转动后笔尖的方向判断转动的度数,验证旋转角度的类别和大小.

图17

图18

问题6通过今天的学习,你对多边形的内角和与外角和有哪些新的认识?

设计意图：通过总结与反思,学生感受到有关内角和与外角和的证明在本质、思路与技巧上的一致性,体会数学知识的相通性,从而实现学习数学的“一以贯之”.

3 教学思考

本节课将三角形的内角和、外角和,多边形的内角和、外角和相关结论的证明过程进行有机整合,实现了“一以贯之”的目标,关注知识的形成过程和发生发展过程,以生为本,顺其自然,循循善诱,水到渠成.

3.1 有效整合,一以贯之

教材依托实验获得新知,内容看似简单,实际知识丰富,如果只按教材授课,那么学生的思维发展会比较局限.笔者将相关知识有机整合,让学生厘清内在关系,站在更高的立足点上去观察问题,将很多问题融会贯通,达到了有效整合的目的.不同的证明方法之间也有着内在的联系,而这些联系最终将回到平角、周角等知识上去,体现了证明方法的“一以贯之”,引领学生从“学会”到“会学”.

3.2 问题驱动,一以贯之

本课的设计采用“问题驱动、一以贯之”的教学方式,利用问题逐步引导,创造一种具体问题情境让学生发现问题、解决问题,促进思维发展.

利用问题引导学生思考三角形内角和的证明方向和本质,尝试思考辅助线的不同添加方式.再利用问题让学生体会多边形内角和公式与其他结论的证明思路一致之处.同时,通过追问再将其思路引入到三角形外角和结论的证明当中,显得自然流畅.

通过问题,学生感受到三角形外角和、多边形外角和相关结论的证明就是将这些外角拼接成一个周角,体会数学的“一以贯之”的类比思想.

3.3 层层突破,一以贯之

教学的核心就是“教学设计”.本节课抓住了教学活动中学生的三次突破,层层推进教学.

第一次突破在问题1:拼接点除了顶点处,还可以在哪里?事实上,这一教学环节的关键就在引出“转化”的数学方法.有了这个环节方法的研究,后续研究多边形的外角和就可“一以贯之”了.

第二次突破在问题3:“外角和是否也可以用这样的方法证明呢?”这既是数学本身发展的需要,更是满足学生的探究欲望的需要,这一环节的探究就显得很开放,学生的自主地位很明显.

第三次突破在问题5:当完成了所有的研究后,并不能体会它的价值.此时转笔实验应运而生.在实验中,让学生尝试将笔端放在边上、外部进行旋转,用实验体会证明方法的“一以贯之”.

数学本身就是相通的,只有立足“一以贯之”,实现“数学相通”,才能更好地帮助学生将数学知识、数学方法与数学思想融合,带领学生站在数学的山顶俯瞰数学,欣赏数学!