“双减”背景下初中数学课堂应教尽教的实践路径

⦿ 四川省内江师范学院数学与信息科学学院 余小芬

⦿四川省内江市第十小学校 邓巧莉

2021年7月,中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(简称“双减”),其中明确提出了“大力提升教育教学质量,确保学生在校内学足学好”,“做到应教尽教,确保学生达到国家规定的学业质量标准”,从根本上强调了提高课堂教学质量的重要意义.学校是教育生态的载体,是学生成长成才的摇篮.课堂是立足学校教育的主阵地,是人才培育的主渠道.教育改革只有深入课堂,才能真实深刻地推动教育的发展.应教尽教,秉持以生为本的教育理念,坚守教师教书育人的初心,将学生的学习质量作为课堂教学的生命线,尽心尽力地引导学生学足学好.具体来说,应教,强调对教学内容的规范,要求教师要严格依据国家课程标准,引导学生完成所在学段应学内容,保障学生学足;尽教,倡导对教学路径的创新,要求教师挖掘和整合教育资源,优化教学方法与手段,引导学生学好.下文基于教与学的角度,结合具体教学案例,谈谈初中数学课堂如何实现应教尽教.

1 教要重视基础知识,学要把握知识背景原理

苏步青先生曾说:“扎扎实实地打好基础,练好基本功,我认为这是学好数学的秘诀.”正所谓合抱之木,生于毫末;九层之台,起于累土;千里之行,始于足下.对数学而言,“基础”是指数学的基础知识(概念、定理、公式等)和基本技能(技能操作的程序和步骤),它是数学学习与应用的基础,是感悟数学思想、积累数学活动经验的载体.数学课堂的应教尽教,首先要求教师要严格依据国家课程标准,以教材为蓝本,向学生讲遍、教足课标中所要求的学习内容,并达到相应水平.同时,又要引导学生超越表层知识的学习,要了解知识的背景由来、梳理知识的结构关系、理解操作背后的数学原理,以此带领学生由单纯记忆和机械操作走向理解和掌握.

例如,在“全等三角形”概念的学习中,理解“全等形”的概念是关键,它为从一般到特殊认识全等三角形奠定基础.因此,这节课从“直观看—实践做—抽象想—类比学”四个层次展开教学活动(如图1).

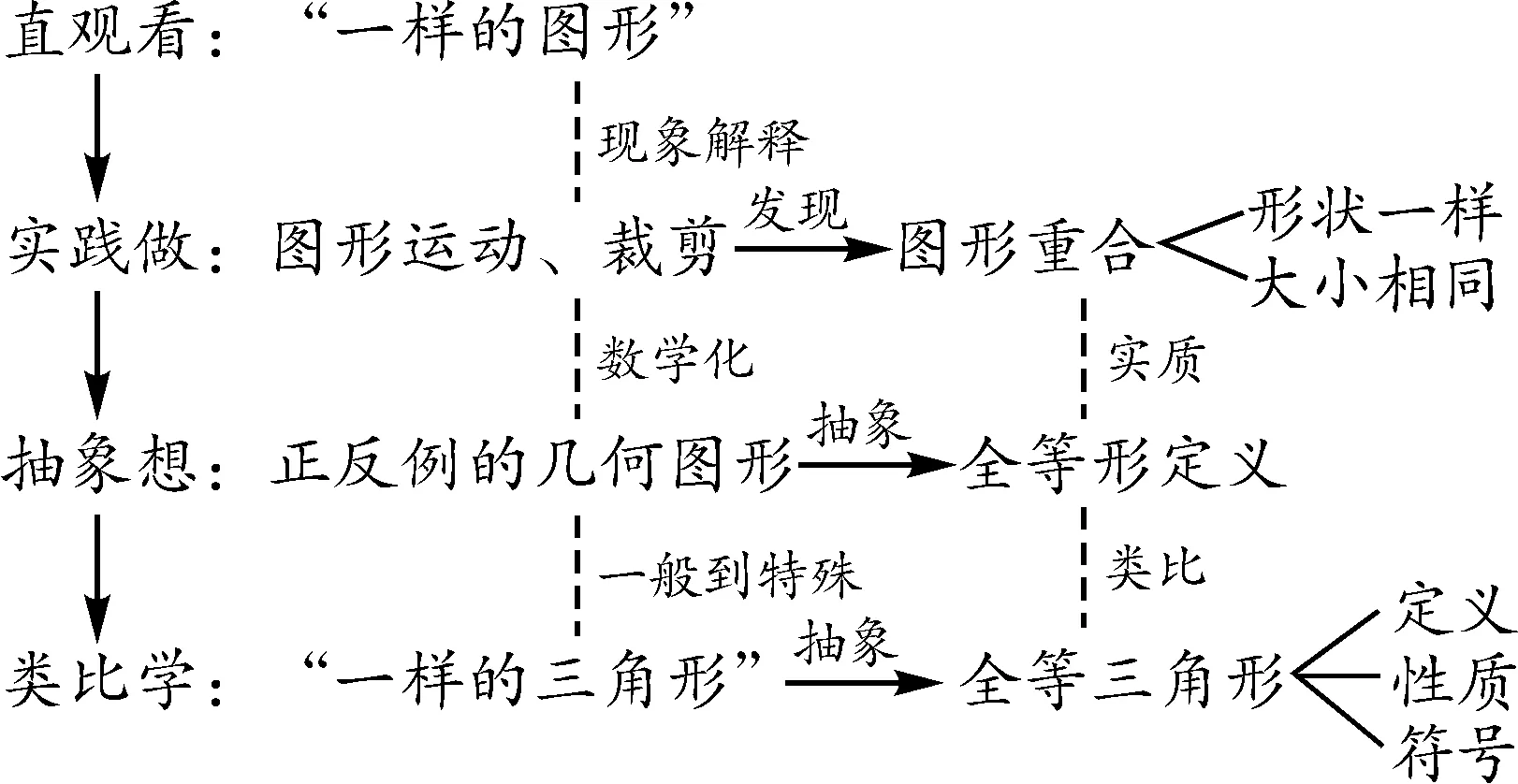
图1

首先,引导学生直观感受生活中“一样的图形”的图形特征,形成对全等概念的感性认识.其次,通过平移、旋转、裁剪等实践操作,认识“一样的图形”实质是“完全重合”,从“形”(形状)和“数”(大小)两个角度体会“完全重合”的内涵.再次,结合正、反例的几何图形,引导学生通过直观想象图形的运动变化感受图形的重合,让概念的理解从生活到数学、从现象到实质、从具体到抽象.最后,鼓励学生类比得到全等三角形的概念:(1)利用一般到特殊的思想理解全等三角形的形状相同、大小相等;(2)由对应边与对应角“完全重合”的图形特征转化为对应边、对应角相等的数量关系,提炼全等三角形的性质;(3)联系和区别数学符号“≌”“=”,认识符号指向的数学实质.

2 教要展示学习逻辑线索,学要体会知识发展脉络

数学学科具有严密的逻辑性,因此培养学生的逻辑性思维也是数学教学的重要任务.数学课堂除了要展现知识的严谨性、科学性,也要给学生提供清晰的学习逻辑线索,引导他们既掌握“是什么”和“怎么做”的知识,也收获过程性知识,以此体验知识产生、发展、结果、应用的丰富过程[1].正如张奠宙先生所指出的,数学教师的任务在于返璞归真,把数学的形式化逻辑链条恢复为当初数学家发明创新时的火热思考.

例如,正比例函数是中学阶段学生系统学习的第一种基本初等函数,它为一次函数的学习提供特殊到一般的类比基础,为后续二次函数、反比例函数,以及高中指数函数、对数函数、幂函数的学习积累活动经验.因此,在正比例函数定义、图象及其性质的学习中,就需要教师“慢”下节奏,引导学生深刻体会函数学习的逻辑线索,掌握概念抽象、图象绘制、性质提炼的思路方法,为后续类比学习其他函数提供经验和动力支持.

首先,以简单实际问题为背景,引导学生列出变量间的对应关系式,归纳表达式的共同特征,抽象函数概念.特别指出,在概念抽象过程中,一定要让学生体会变量间的对应变化关系,理解问题中的函数实质,由此基于函数概念、结合表达式特征对正比例函数下定义,降低学生对函数的认知困难.其次,在图象的认识中,要让学生经历图象的绘制过程,掌握列表、描点、连线的绘图“三步曲”,并在比较和优化中确定“两点一线”的画图方法,在数形结合中领悟正比例函数的内涵.最后,对函数性质的提炼,引导学生宏观把握图象分布范围(自变量、函数值的取值范围,图象在坐标系的位置等),微观描述图形特征(过定点、增减性、对称性等).图2的正比例函数学习流程连通了数学知识、思想方法、技能策略,对其他基本初等函数的学习具有高度的概括性、迁移性,发挥着先行组织者的作用,可以帮助学生形成良好的认知印象.

图2

3 教要渗透数学思维方法,学要获得自主学习工具

陶行知先生曾说:“活的人才教育不是灌输知识,而是将开发文化宝库的钥匙,尽我们知道的交给学生.”“好的先生不是教书,不是教学生,乃是教学生学.”在科技日新月异的今天,机器模拟人类和其他生物的自然智能应用越来越广泛,未来我们将进入更多的科技发展“无人区”.为使教育所培养出的学生能适应未来的学习生活,教学一定要以发展学生的核心素养为立足点,尤其是发展机器无法具备的能力,如自主学习、实践创新、反思能力等.然而,这些关键能力并非与生俱来,其培养也不可能一蹴而就,需要学生在长期的学习中逐渐积累形成.对数学而言,数学思想方法是数学学习研究所依赖的根本,是数学学科发生、发展的精髓,是建立数学和用数学解决问题的指导思想[2],是学生开展自主学习的有利工具.教学中,教师应引导学生透过现象看本质,理解知识蕴含的数学思想,掌握学习研究的数学方法,体会数学学科的思维特点,以此获得自主性的学习工具.

例如,在“探索勾股定理”的学习中,设计如图3的教学板书,清晰明了地展示勾股定理发现、猜想、证明、拓展的学习线索,生动形象地展现内隐于数学活动过程的思想方法,为其他数学命题的学习提供研究工具.

图3

如在定理发现中,鼓励学生要善于联系,敢于联想,勇于实践.在定理的猜想与证明中,引导学生体会数形结合、从特殊到一般的数学思想,把握先猜后证、特值引路、类比迁移的数学方法,体会数学学习中合情推理的意义,体验数学证明的严谨.在从原命题到逆命题的拓展中,为学生提供构建数学命题体系的研究方法,促进学生理解命题间的相互关系,增强问题研究能力.史宁中教授指出:“我们需要清晰的认知,但更需要个人的亲历.”亲历即是要关注知识学习的过程性,重视个体活动的切身体验性.学生只有经历尝试与反思、矛盾与挣扎,才能在思维方式和实践体验方面形成对自身有价值、可利用的新观念.

4 教要交融智慧情感艺术,学要实现健康全面发展

“师者也,教之以事而喻诸德也.”在数学教学活动中,教师要把握学生的成长规律,利用数学学科的独特性,挖掘数学知识背后的育人价值,找准数学教学立德树人的切入点,充分发挥数学教学“文道合一”的作用,不仅要教会、教好学生数学知识,更要帮助他们塑造人格操守,树立正确的价值取向和思想观念,实现知、情、意、行等全面发展.正如教育家于漪老师所指出的,虽然只是短短的一堂课,但是学生的生命是在这一节一节课堂中度过的,每一堂课都是学生拔节孕穗的关键期.

例如,“全面调查”是“数据的收集与整理”章节的起始课,也是初中阶段统计学领域的开篇.因此,与常规新课相比,本节课除了要介绍全面调查的具体操作,还应让学生体会统计学学习的意义,经历简单统计活动的一般过程,形成用数据“说话”的意识,同时,在学习与实践活动中,更要让学生形成严谨求实的做事态度,树立社会责任担当的意识.例如,教学“整理数据”阶段,在利用“正”字划记中,一方面让学生体会“正”字有五笔方便读数,同时其笔直的横、竖结构方便书写记录,这符合人们长期以来的计数习惯.另一方面,可以借用“正”字的端正与正气的积极含义,引导学生做人要品行端正,做事要正大光明,如在统计调查中,处理分析数据要求真求实,不弄虚作假,要遵守和履行信息伦理,要有社会责任意识.通过对“正”的解读,既能让学生体会符号化记录数据的优势,又能引导他们树立正确的价值观念.

叶澜教授曾说,“我们要从生命的高度看课堂教学,让课堂焕发出生命的活力”,“让课堂成为学生生命有意义的构成部分”.应教尽教,尽管字面上强调的是“教”,但“教”是为了“学”、围绕“学”、服务“学”.落实课堂教学的应教尽教,教师要尽力结合自身的知识能力,尽心展现教学的艺术手段,引导和促进学生在学习过程中深度参与,包括兴趣的激发、认知的递进、思维的碰撞、实践的体验、情感的投入,以此让知识的学习落地生根并转化为减轻学生学业负担、发展学生核心素养的行动力.