深耕“数学实验” 共话“做中学”引领“深度学习”*

⦿ 江苏省宜兴市丁蜀镇东坡中学 沈 静

近年来,“数学实验”由于融观察、操作、思考于一体,成为广受师生欢迎的一种学习方式.诚然,数学实验与“做中学”理念相吻合,的确能让学生“学思创共生”,从而使学生成为真正的探索者,在深度探究中开展深度学习.因此,教师需大胆将数学实验融入课堂教学,深入探寻实验设计的有效策略,让数学实验有效开展,引导学生在“做中学”,从而在独立思考、自主操作和深度探究中实现深度学习[1].

1 “做中学”主张下数学实验的教学前提

“做中学”的教学模式是教育学家杜威提出的,他主张借助手、脑、耳、口等多个感觉器官真实地接触到具体事物,以此积累知识和经验,并借助于深入思考完成感性认识到理性知识的过渡,最终达成问题的解决.事实上,数学实验源自“做中学”的教学主张,着重强调学习过程和学习体验.笔者在数学实验中所追求的正是:通过“做”的过程培养对数学的兴趣,切实体验数学知识和思想方法,引领深度学习,提升数学素养.不难看出,“做”的过程,就是数学化和再创造的过程,想要让“做中学”的理念能够在数学实验中落实到位,需要教师、学生、师生关系这三个条件.

围绕上述理解,笔者大胆设计了“用纸折特殊三角形”的数学实验课,以期借助“做中学”的教学主张,引领学生通过动手折、剪、拼等操作活动,探究折纸数学,进而发现特殊三角形的折法和特殊三角形的三边之比等,最终能解决由特殊三角形组成的一类三角形解直角三角形的应用类问题.

2 “用纸折特殊三角形”的数学实验课设计

2.1 教学目标

本节课先引导学生学习并掌握特殊三角形的折法和三边比,为后续解决相关问题储备实验感知;然后再安排与之相应的应用题,引领学生在深度思考、探究中解决问题,实现深度学习.

通过创设良好实验环节和精准设问,引领学生体验“操作—归纳—发现—验证”的研究过程,感受生活中的数学,获得丰富的数学活动经验,提高动手操作能力和语言表达能力,发展数学思维[2].

2.2 素材准备

(1)几何画板课件.

(2)矩形彩纸三张,且编号及大小设定如下:全班统一的是①号和②号矩形彩纸;没有统一的③号矩形彩纸有两种——一种是大小设定可以确保在活动3将长方形彩纸对折后得到的直角三角形的短直角边的长度等于活动2得出的三角形短直角边长度;另一种则可以确保在活动3将长方形对折后得到的直角三角形的长直角边长度等于活动2得出的三角形长直角边.

2.3 过程设计

2.3.1 激趣导入

PPT呈现各种幼时折纸作品图片,自然引出课题:折纸中的数学,即用纸折特殊三角形.

2.3.2 操作实践

活动1：先用①号矩形纸折出一个三角形,其内角分别是45°,45°,90°(如图1);再剪下该三角形,并说一说该三角形的三边比.

图1

设计说明：通过一个简单易操作的活动,激起学生的兴趣,调动学生参与的积极性,为后续真正的数学实验探究作好铺垫,让学生怀揣兴趣和欲望开启真正的数学探究之旅.

活动2：

(1)观看微课后,学着用②号矩形纸片折出一个三角形,其内角分别是30°,60°,90°(如图2).然后用自己的语言说明它是符合以上条件的三角形.

图2

(2)剪下该三角形,并猜测AC与BC之比,再利用折纸法予以证明.

(3)你知道该三角形的三边之比吗?

设计说明：由于直接探究活动2需要耗费大量时间,相对而言,说明“所折三角形即为所求”要比折出这个三角形更具有探究性,据此笔者在反复揣摩后决定借助微课提示学生折纸方法,并留足时间给学生证明,让学生在合作学习中生成认识,发展逻辑思维能力.这样看似“随意”实则“有心”的设计,让数学课堂的推进紧凑而有序,促进学生高阶思维的提升.

活动3：试着用③号矩形纸片折出一个三角形,其内角分别是30°,30°,120°(如图3).再剪下该三角形,说一说它的三边之比,并予以证明.

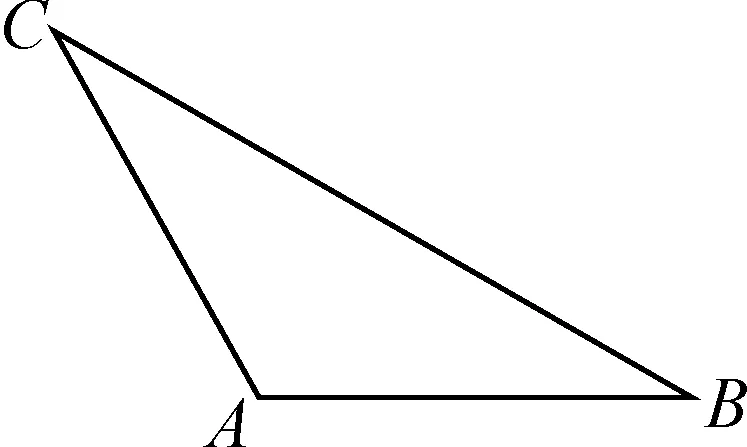
图3

设计说明：在活动2的铺垫提示下,活动3变得简单易行,学生可以较好、较快地完成任务,并信心满满地投入到之后的探索中.

2.3.3 巩固提升

活动4：先归纳以上三种三角形,例如“一个内角分别是45°,45°,90°的三角形的三边之比是……”,再试着用手中的三角形拼成一个新三角形,猜想并证明其三边之比.

设计说明：有了前3次活动的指引,学生再次展开实践活动并解决问题就显得轻松多了,很快获得了结论.而深入实验内部可以发现,实验本质与中考考查的题型相似,如此,在趣味实验的过程中学生获得了对数学知识的本质理解,完成了思想与实践的对接,在各具特色的探索下形成了数学实验创新思路.

2.3.4 应用拓展

问题1如图4,某工程队打算修筑一条笔直的公路贯穿相距2 km的A,B两地,经过测量,发现距离A地北偏东60°方向、B地的西偏北45°方向的C处有一个公园,其半径是0.7 km.那么,该工程队计划修建的公路会穿过该公园吗?为什么?

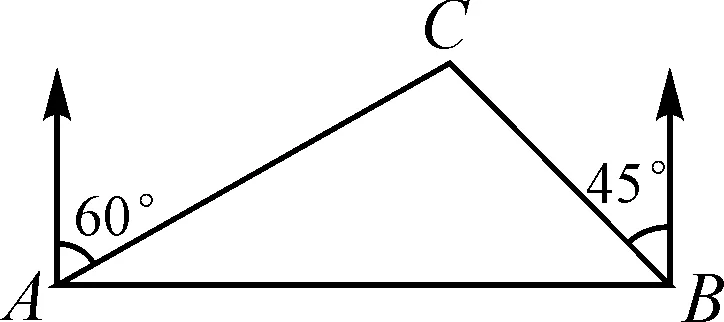
图4

问题2如图5,已知红红用测角仪于A处观测到气球C的仰角是30°,接着她沿着正对气球的方向前进50 m至B处,又观测到此时气球C的仰角是45°.若测角仪高度是1 m,试求气球C的高度.

图5

设计说明：在这一环节的探究中,学生能将上述四次探究活动的经验运用到拓展环节的问题解决中来,并做到人人参与、独立思考、自主探究,使“难”题不难,实现了真正意义上的深度学习,最终感受到数学解题中化难为易的思维方式,从而真正意义上激发了学生的学习热情和提高了学生的学习效果.

3 小结

数学实验首先需要教师积累厚实的教学经验,极好地沟通知识与学生、教学、课程的联系,营造良性互动的学习氛围,让学生感受的不仅仅是单纯数学知识的习得,还是在操作中感受数学的生动、丰富,从而在深度学习中发展数学素养[3].

为了培养有智慧、有素养的学生,“做中学”理念下的探究具有广阔的前景.一方面,在数学实验中,“做中学”可以作为具有认知训练意义的、既生动又创新的教学行为,让学生在独立思考、深入操作、深度探究和深度合作中深度学习,在沟通交流、动手操作、推理论证、语言表达等能力上不断飞跃.另一方面,在数学实验中,“做中学”通过教师课前设计与现场调控,给足了学生智慧熏陶,极好地改善了学生的思维方式,让学生在不断猜想中提升直觉思维,发展理性思维和创新思维能力,从而为学生的终身发展提供助力.

总之,深耕“数学实验”,用“做中学”的理念让学生“学思创共生”,形成探究性学习的典型形式,为学生赋予广阔的思维空间,点亮鲜活的思维火花,从而实现“深度学习”,促进学生数学核心素养的提升.