基于广义积分变换法海洋温差能大口径冷水管强迫振动分析

谭 健,张 理,王 冲,张玉龙,张 玉,段梦兰

(1.中国石油大学(北京) 安全与海洋工程学院,北京 102249;2.南方海洋科学与工程广东省实验室(湛江),广东 湛江 524005;3.中国科学院 声学研究所噪声与振动重点实验室,北京 100190)

海洋温差能是海洋能中储量最大、最稳定的清洁可再生能源,也是可再生能源中唯一无需储能系统可以实现稳定、可控供电的能源。海洋能海洋温差能发电(ocean thermal energy conversion,OTEC)是利用深层冷海水与表层温海水之间的温度梯度来运行热机并产生有用功,通常是以电力的形式[1]。OTEC系统装置可分为岸基式和浮式[2],如图1所示[3]。而冷水管(cold-water pipe,CWP)是海洋温差能发电系统装置中一种新颖的、最为关键的部件,是浮体平台和深层海水之间的输送通道[4]。OTEC装置应用的机械问题主要集中在两个方面:汽轮机和冷水管[5]。大口径和超长的冷水管在复杂多变的海洋工况下,其强迫振动响应直接影响OTEC装置的工作条件,同时也是制约海洋温差能发电商业化的因素之一。因此开展大口径冷水管的强迫振动分析,以为其初期设计提供一定的指导作用。

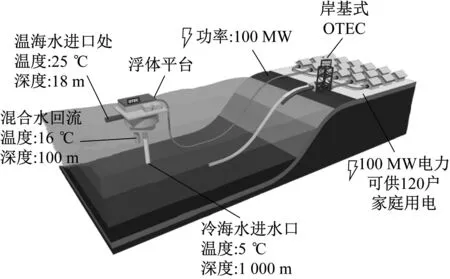
图1 海洋温差能发电工作原理

自冷水管的概念第一次被提出到应用于OTEC系统中,冷水管的振动响应研究一直都是OTEC系统装置前期设计的重点关注对象。冷水管的设计问题可分为三个主要问题:极限分析[6-8]、船-管耦合分析[9-10]和管道振动分析[11-12](涡激振动和内流引起的振动)。大量学者通过理论、有限元和实验方法验证了内流流动将引发管体的不稳定[13-15],然而鲜有文献针对大口径冷水管的强迫振动进行分析。但作为一种典型的输流管道,众多学者对输流管路的自由振动和强迫振动做了大量的研究工作。黄灿等[16]采用分数导数算子研究了振动系统在谐波激励下的稳态响应,并讨论了分数阶导数项对刚度和阻尼的影响。王剑等[17]通过提出理论-实验混合计算方法,研究了考虑质量偏心的阶梯梁-基础的强迫振动,发现在垂向激励下质量偏心对系统的垂向位移响应无影响,但会产生纵向位移响应。赵千里等[18]基于格林函数法推导了固定-弹性支承式输流管的格林函数,并得到了扰度的解析表达式,分析了扰度与激振位置、激振频率、内流流速、弹簧刚度和质量比的关系,并提出该方法可适用研究任意支承形式和多个激励的强迫振动问题。此后针对外部载荷和内流共同作用下输流弯管的强迫振动问题,基于修正的不可伸长理论,研究了正切方向的夹角、激振频率和激振位置对切向位移稳态响应的影响[19]。孙志礼等[20]利用格林函数法研究了两端支承输流管在集中载荷和分布载荷下的强迫振动并推导了封闭的精确解。范瑾铭等[21]基于格林函数法获得旋转输流管双向耦合强迫振动的解析解,分析了内流气体体积分数、双相流流速、轴向压力、弹簧刚度系数对管道动力学特性的影响。发现流速和转速共同作用将导致系统产生特殊的共振带。Tan等[22]建立了输流管道耦合振动的非线性Timoshenko模型,通过开发的有限差分法(finite difference method,FDM)研究了黏弹性管材受迫振动的幅频曲线,结果表明大流速、大振动幅度或较短的管道长度使得Timoshenko模型更适用于管道的响应预测。

在研究输流管道的动力学响应问题主要包括振动模型的建立和求解,大多学者基于此类问题开展相关工作。从最为基本的有限单元法求解振动问题,到便捷、高效率、高精度的求解方法,国内外学者取得了大量的成果。例如:Ni等[23]采用微分变换法(differential transform method,DTM)研究了几种典型边界条件下管道自由振动问题,并验证了该方法具有高精度和计算效率。包日东等[24]利用微分求积法(differential quadrature method,DQM)研究了一般端部条件下输流管的稳定性问题,并分析了弹性支承系数对管道稳定性的影响。Li等[25]采用传递矩阵法分析了支座、结构特性和流体参数对管道动力响应和固有频率的影响规律,表明采用最佳支座和结构特性有利于降低管道振动。金基铎等[26]采用伽辽金法推导了梁弯曲振动的频率方程和振型函数表达式,研究了扭转刚度、重力系数和轴向预紧力对管道临界流速的影响特性。近几年,格林函数法(Green’s function method,GFM)常被用来求解梁的强迫振动问题。Li等[27]基于格林函数法研究了Timosheko梁受迫振动的动力解,并考虑了阻尼对梁振动的影响。但格林函数法的应用通常需要依赖问题的对称性和边界条件,若问题的对称性不明显或边界条件复杂,需进一步简化假设或引入额外的假设,从而导致解的准确性和适用性问题。广义积分变换法(generalized integral transform technique,GITT)是一种更为准确、简单和快速求解高阶非线性偏微分方程的半解析解方法,此方法成功应用于轴向移动梁[28]、轴向移动Timoshenko梁[29]、轴向移动正交各向异性板[30]、损伤的欧拉-伯努利梁[31]、尖端偏心质量的悬臂梁[32]和输流管道[33-35]的动态响应等。为此,本文采用广义积分变换法求解大口径冷水管强迫振动问题。

本文针对大口径冷水管强迫振动问题,基于Euler-Bernoulli梁理论,考虑黏弹性耗散系数、阻尼比和质量比对振动特性的影响,建立了大口径冷水管强迫振动运动响应计算分析模型,结合GITT法,推导了管道在不同边界条件下的特征值和特征函数,通过与同伦摄动法对比,验证了该方法的高精度和有效性,并综合分析了在均布载荷、线性变化的静水压力、集中载荷和周期载荷作用下内流、黏弹性耗散系数、周围环境阻尼比、质量比、激振位置和激励频率对管道横向位移的影响。

1 模型描述

采用Euler-Bernoulli梁模型描述海洋温差能大口径冷水管强迫振动的力学行为,如图2显示了在外部激励下输送流体的管道示意图,本文基于Paidoussis所提出的模型[36],其基本假设为:①x轴即为中性轴,无拉伸也无压缩;②保持平面假设,即变形前后保持横截面与中性面垂直,忽略剪切变形的影响;③材料是线弹性的,管道为各向同性的;④忽略x方向的加速度和转动惯量的影响;⑤x-y平面是主平面,管道在主平面内振动;⑥忽略管道与流体之间的摩擦;⑦管道长径比足够大,横向位移与管道长度相比较小。由此建立如下冷水管横向振动控制方程

(1)

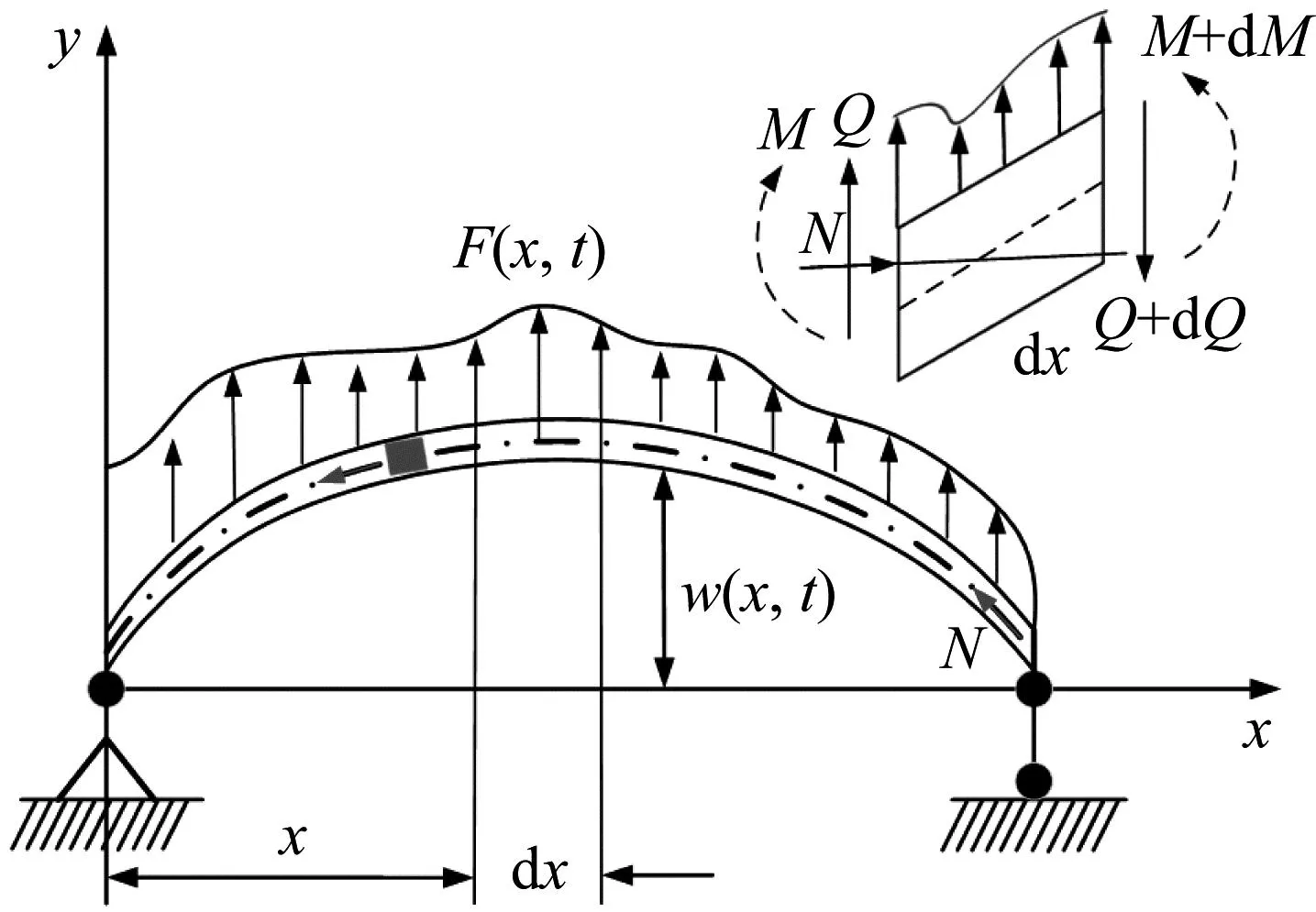
图2 承受横向动载荷梁模型

式中:EI为抗弯刚度;w(x,t)为横向位移;L为管道长度;m为单位长度上管道自身质量;M为单位长度管内流体质量;T(x)为轴向静等效张力;Ttop为顶部张力;U为管内流速;c为周围环境的阻尼比;F(x,t)为外部激励载荷;t为时间。式(1)左边的项依次为弯曲力、轴向张力、离心力、顶部张力、科氏力、外部阻尼力和惯性力。

单位长度管上x处t时刻的外部激励为F(x,t),可表示为

F(x,t)=F0δ(x-x0)

(2)

式中:F0为激励载荷类型;x0为激励位置。冷水管在各种载荷下的示意图,如图3所示。

(a) 均布载荷

轴向静等效张力T(x)可表示为

(3)

式中:冷水管外部压强P0(x)=ρfgx+Δp,ρf为内部流体密度和海水密度,冷水管内部压强Pi(x)=ρfgx,其中Δp为同一深度下管内外压差,而此压差取决于进水口的几何形状,其取值范围为0.5ρfU2～ρfU2之间[37],本文取其值为ρfU2;Tbt为冷水管湿重,Tbt=(ρr-ρf)·ArgL,ρr为管道密度,Ar为管道的横截面面积;Twc为底部配重块自重,Twc=ρrArgL,顶部张力Ttop=Twc+Tbt。

管道结构阻尼是结构运动时能量耗散因素之一,所产生阻尼应力与材料的应变速率有关,可采用Kelvin-Voigt阻尼模型[38]来表示

(4)

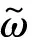
全面考虑黏弹性耗散、阻尼比、管内外压差和内流对管道横向振动所产生的影响,则大口径冷水管横向振动控制方程为

(5)

通过引入无量纲系数以简化冷水管横向运动控制方程,无量纲系数如下

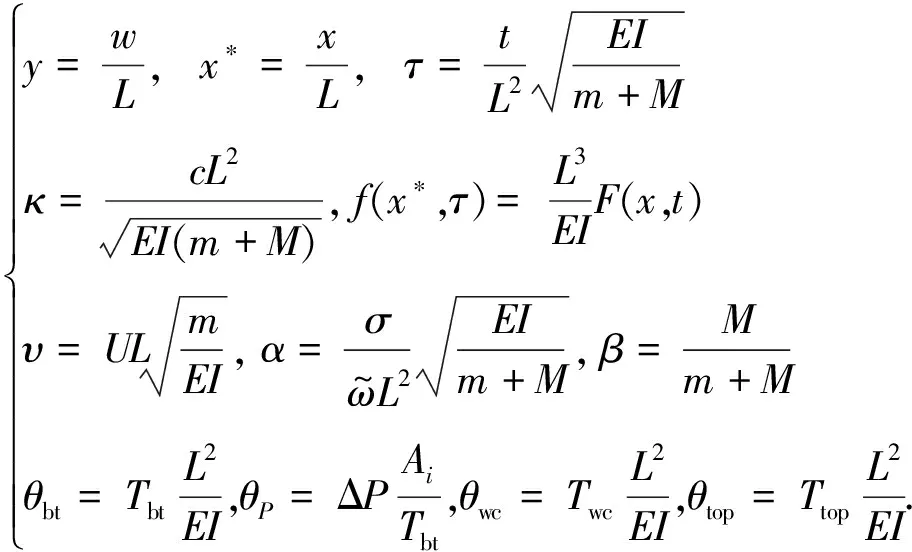
(6)

为方便书写,继续采用x以代替x*;则无量纲化后的控制方程为

(7)

给定管道系统一个初始扰动,其表达式如下

(8)

对于海洋温差能发电系统,冷水管的顶部约束可视为不可移动的理想的固支和简支两种;而在运行工况下的冷水管,其底部的约束可分为固支、简支、自由和配重块四种。不同边界条件下,管道的位移、转角、弯矩和剪力不同的,表1中给出了本文模型中6种无量纲的边界类型。

表1 模型的6种边界条件

2 广义积分变换法求解

根据广义积分变换法求解振动方程非线性问题原理,主要是将四阶偏微分方程通过分离变量法降阶为二阶常微分方程,变换求解过程可分为三大步骤:第一步,特征值和特征函数的确定;第二步,引入积分变换对;第三步,方程逆变换与求解。

2.1 特征值求解

温差能大口径冷水管横向振动控制方程的特征值问题为

i=1,2,3,…和k=1,2,3,4,5,6

(9)

假定冷水管两端的边界条件为固支-加配重块,其无量纲化的函数表达式为

(10)

此时,yi(x)和λi分别为特征值问题(9)的特征函数和特征值,因特征函数满足正交性

(11)

式中,δij为克罗内克符号,当i≠j,δij=0;当i=j,δij=1。由此可得,归一化积分为

(12)

特征值问题(9)的特征函数为

yi(x)=sin(λix)-sinh(λix)+

(13)

特征值问题(9)的特征值为

(i=1,2,3…)

(14)

进而得到Ni的值为

Ni=1.0,i=1,2,3…

(15)

特征函数的特征向量为

(16)

同理可求得冷水管在其他5种边界条件下的特征函数与特征值,如表A.1所示(见附录A)。

2.2 引入积分变换对

对控制方程(7)进行积分变换,引入横向位移积分变换,如下:

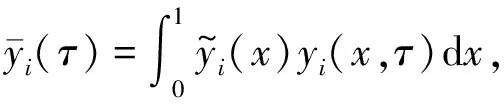
(17)

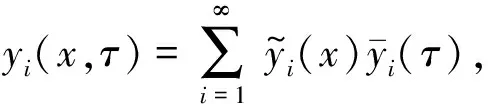
(18)

2.3 方程变换与求解

(19)

其中各个系数表达式为

(20)

同理,对初始条件进行积分变换,以消除空间坐标,可得:

i=1,2,3…

(21)

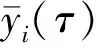
AY=d

(22)

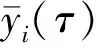
3 解法的收敛性与有效性

为了验证GITT方法的收敛性,稳定收敛条件为:当展开项数目NW取4、8、12、16和20,管道的横向位移收敛于特定的值,允许存在极小偏差。本章选取管道边界条件为两端固支(C-C)下的自由振动,内流流速υ=0.2,外流流速μ=0,管道参数与流体参数如表2所示。其中,开展项数目NW分别选取4、8、12、16和20。当无量纲时间τ=20时,不同展开项数下管道的位移如图4所示。依据图4可知,当开展项数目NW=4时,管道位移相对展开项数8、12、16和20较小,且管道振型与上述展开项数目相比并不收敛;当NW≥12时,管道振型已具有良好的收敛。因此在之后的计算时,可选取展开项数目NW=16。

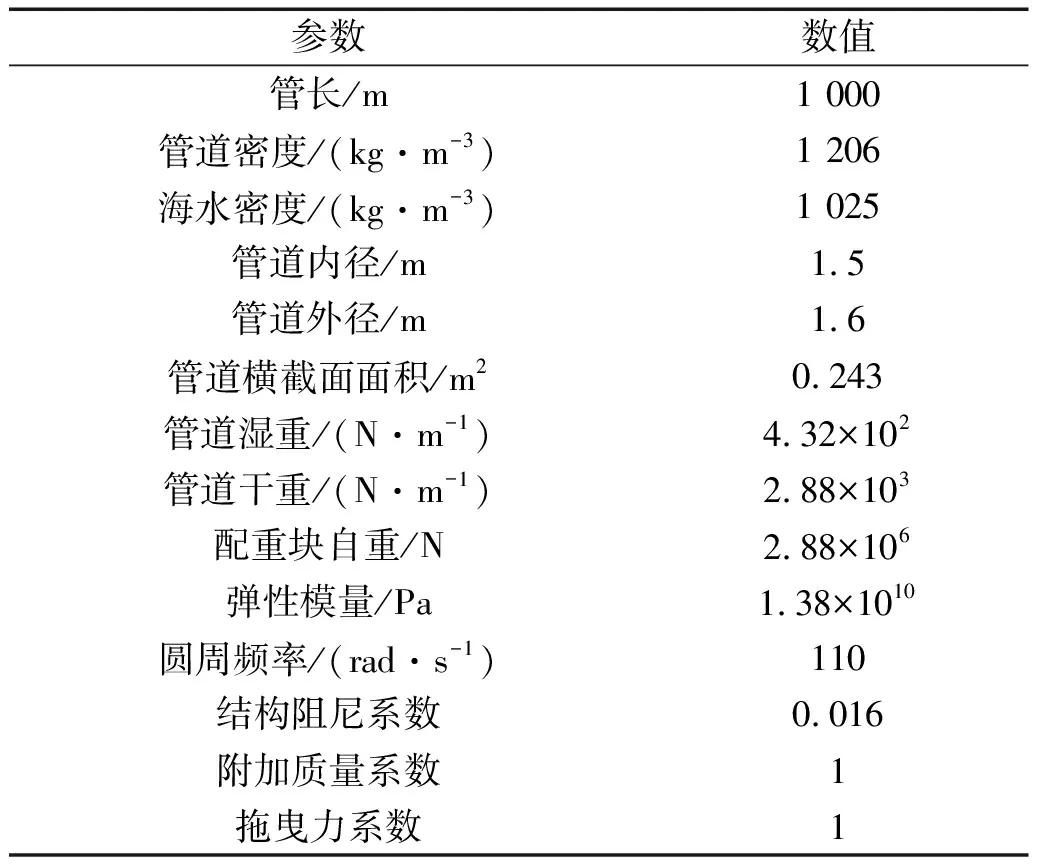
表2 冷水管道参数

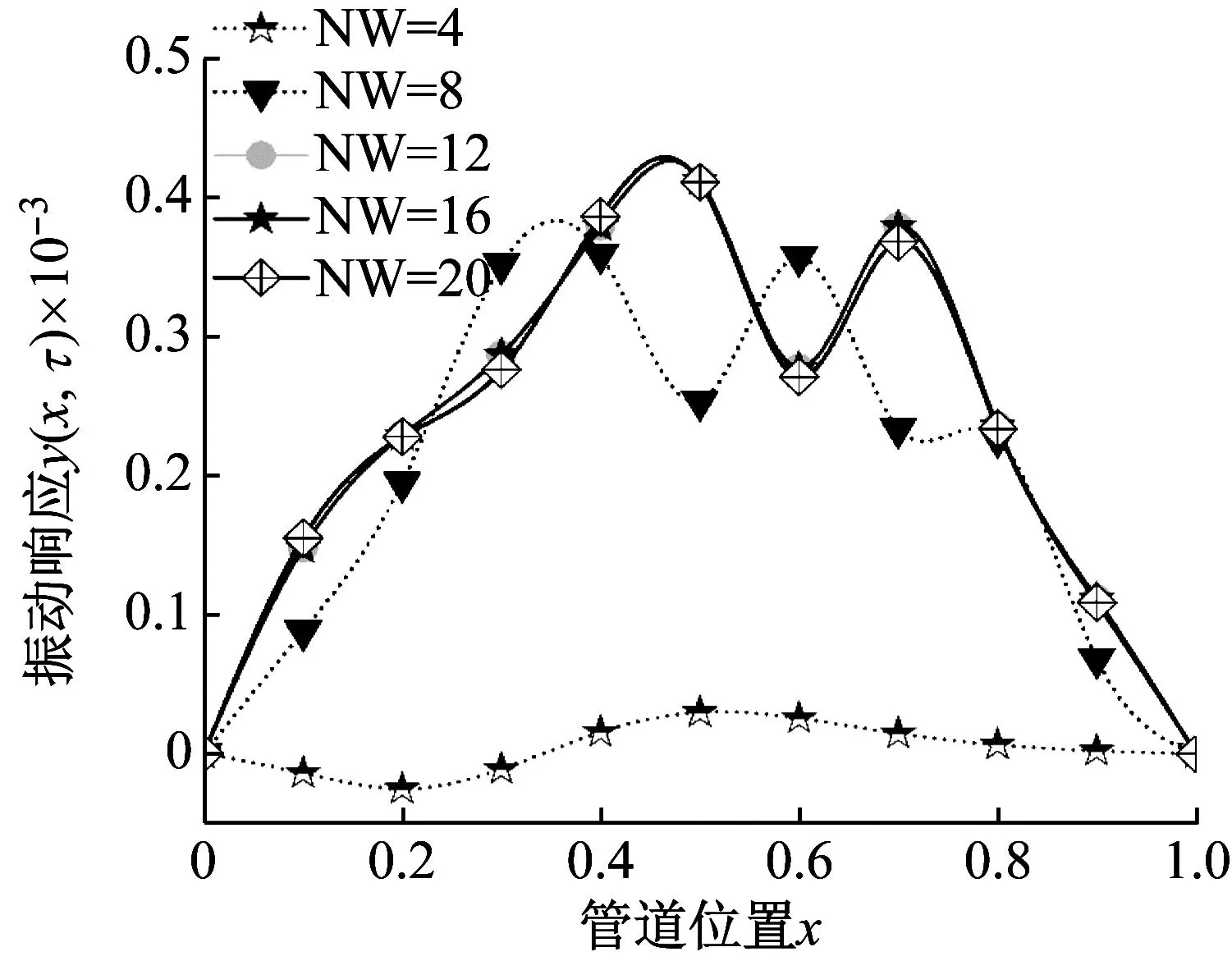
图4 不同展开项数下管道位移对比图

为了验证GITT方法的有效性,将GITT方法得到的结果与Xu[39]所采用的同伦摄动法(homotopy perturbation method,HPM)得到的结果做对比,其中ωf为一阶固有频率,υf为临界流速,如图5所示。可以看出,在固支-固支、固支-自由和简支-简支的边界条件下,管道的自振频率随内流的增加而逐渐减小,直至为零。GITT方法计算得到的一阶固有频率与HPM方法所得结果相对比,其相对误差小于4.5%。从而验证了GITT方法的有效性。

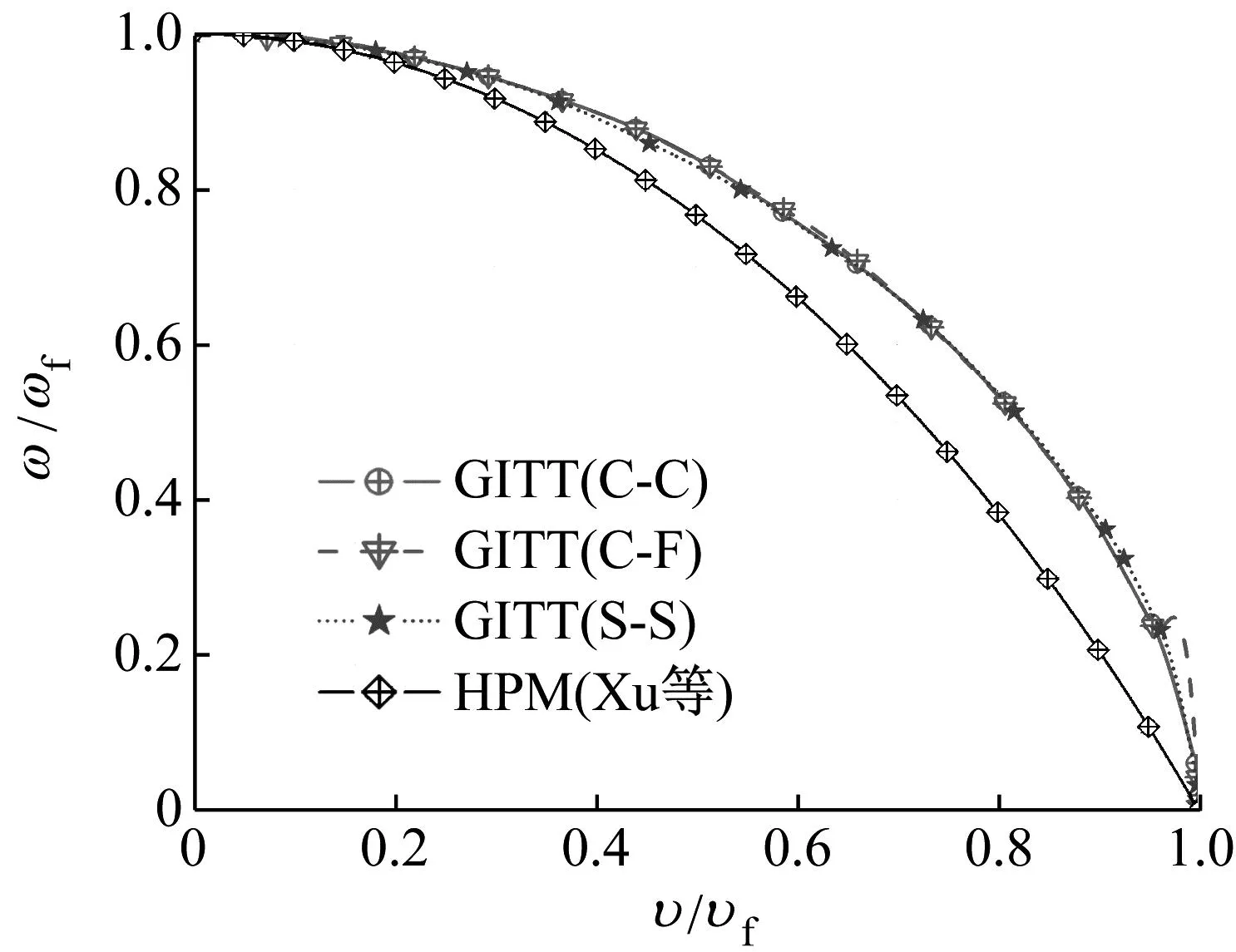
图5 一阶固有频率随内流流速变化

4 分析与讨论

本章以海洋温差能大口径冷水管为研究对象,研究考虑在四种不同载荷作用下内流、黏弹性耗散系数α、周围环境阻尼比κ、质量比β对管道振动特性的影响:① 均布载荷F0=q0;② 线性变化静水压力F0=q0x/L;③ 集中载荷F0=P;④ 周期载荷F0=Psin(ω0t),如图3所示。大口径冷水管所受外部激励无量纲化后的表达式为

f(x,τ)=f0δ(x-a)

(23)

式中,a为式(2)中x0的无量纲形式,即a=x0/L,f0为激励载荷无量纲化。

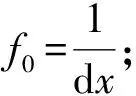
4.1 均布载荷作用下管道振动特性分析

本小节研究在均布载荷作用下,内流流速和阻尼比对冷水管振动特性的影响,其中选定管道边界条件为C-C和S-S,时间τ=20,其他参数从表4中选取。图6显示了在黏弹性耗散系数α=0.01、质量比β=0.5、周围环境阻尼比κ=0和边界条件为C-C下,管道横向位移随内流流速变化的发展规律曲线。

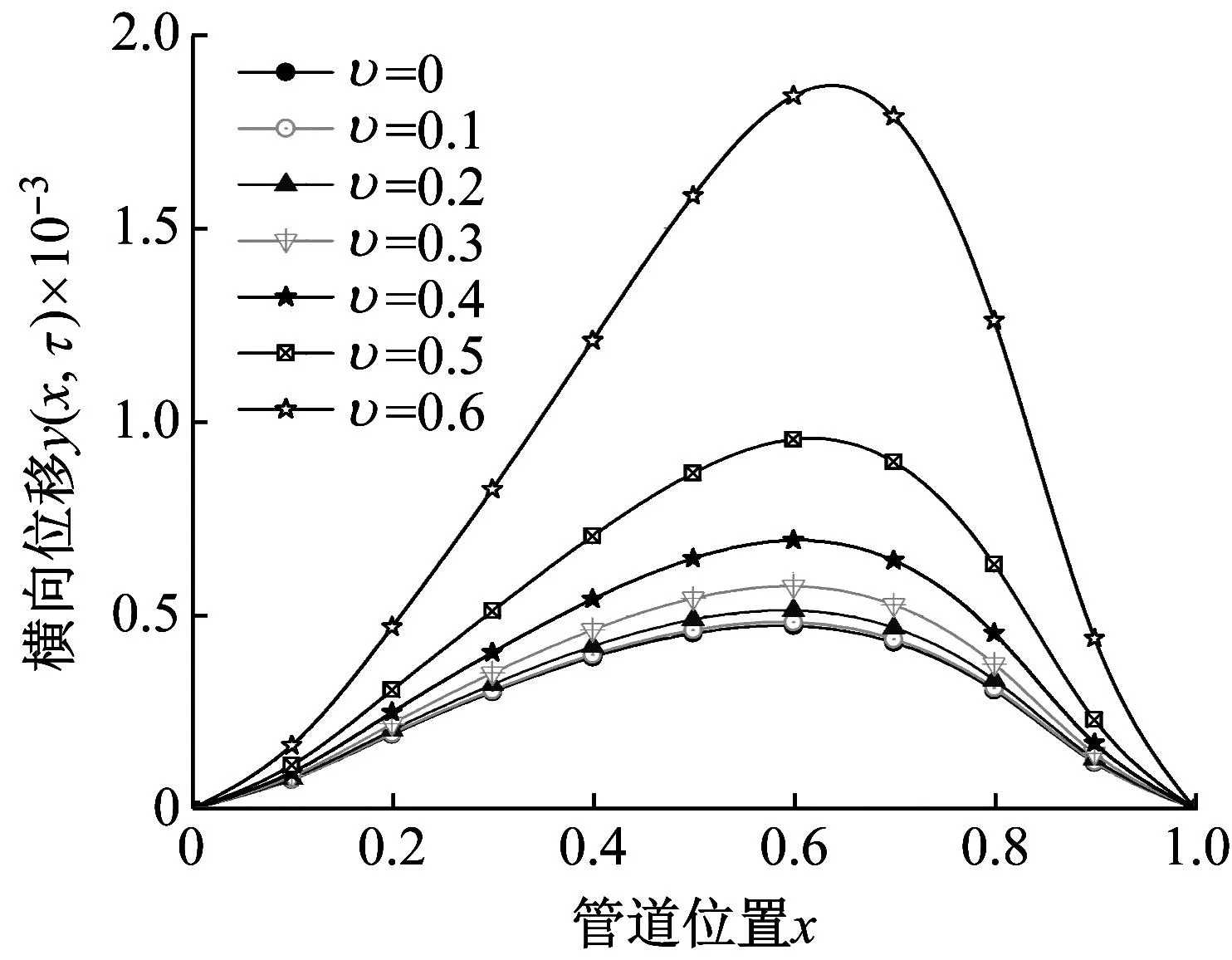
图6 均布载荷作用下管道横向位移与内流流速的关系曲线(C-C)

从图6可以看出,在均布载荷作用下,随着管道位置x的增加,管道横向位移先增大后减小。随着无量纲内流流速的不断增大,管道整体横向位移呈现逐渐增大的趋势。当无量纲内流流速较小时,管道整体横向位移的最大值ymax(x,τ)出现在x=0.60位置处,而当υ=0.6时,管道的ymax(x,τ)相较于其他流速对应的ymax(x,τ)要大很多,一方面是因为内流流速的增大致使离心力增大,另一方面在此流速下对应的振动频率与管道的某一阶固有频率相近。由GITT方法求解此模型,其结果通过快速傅里叶变换(fast Fourier transform,FFT),求得管道振动频率为26.727 5,对应的ymax(x,τ)=0.001 869,对应的管道位置x=0.63。

进一步,图7给出了在均布载荷作用下,不同黏弹性耗散系数α管道中点最大的横向位移随周围环境阻尼比κ发展的曲线图,其中边界条件为C-C和S-S,所对应的无量纲内流流速分别为0.6和0.1,质量比β=0.2。从图7(a)可以发现,在边界条件为C-C时,阻尼比κ对无黏弹性耗散系数管道中点最大横向位移影响十分显著。随着阻尼比逐渐增大,管道最大横向位移整体呈现减小趋势。在α=0时,管道最大横向位移在κ∈[0.1,0.3]范围内几乎不发生改变,而在κ=0.4处急剧减小,而在α≠0时,管道最大横向位移并无类似现象。当黏弹性耗散系数分别为0,0.000 5和0.001 0时,管道最大横向位移进入平滑稳定减小阶段所对应的阻尼比分别为0.6,0.3和0.3。值得注意的是,黏弹性耗散系数能明显减小管道最大横向位移。根据图7(b),在边界条件为S-S时,随阻尼比逐渐增大,管道最大横向位移呈现先逐渐减小,进而急剧减小,后进入平滑稳定减小阶段趋势。当黏弹性耗散系数分别为0,0.000 5和0.001 0时,管道最大横向位移进入急剧减小阶段所对应的阻尼比分别为0.4,0.3和0.2,而进入平滑稳定减小阶段对应的阻尼比均为0.6。此外对比图7(a-1)和(b-2)的管道中点时间历程可以发现,增大阻尼比κ可改变S-S边界条件下管道的振型,但对C-C边界条件下管道的振型无影响。

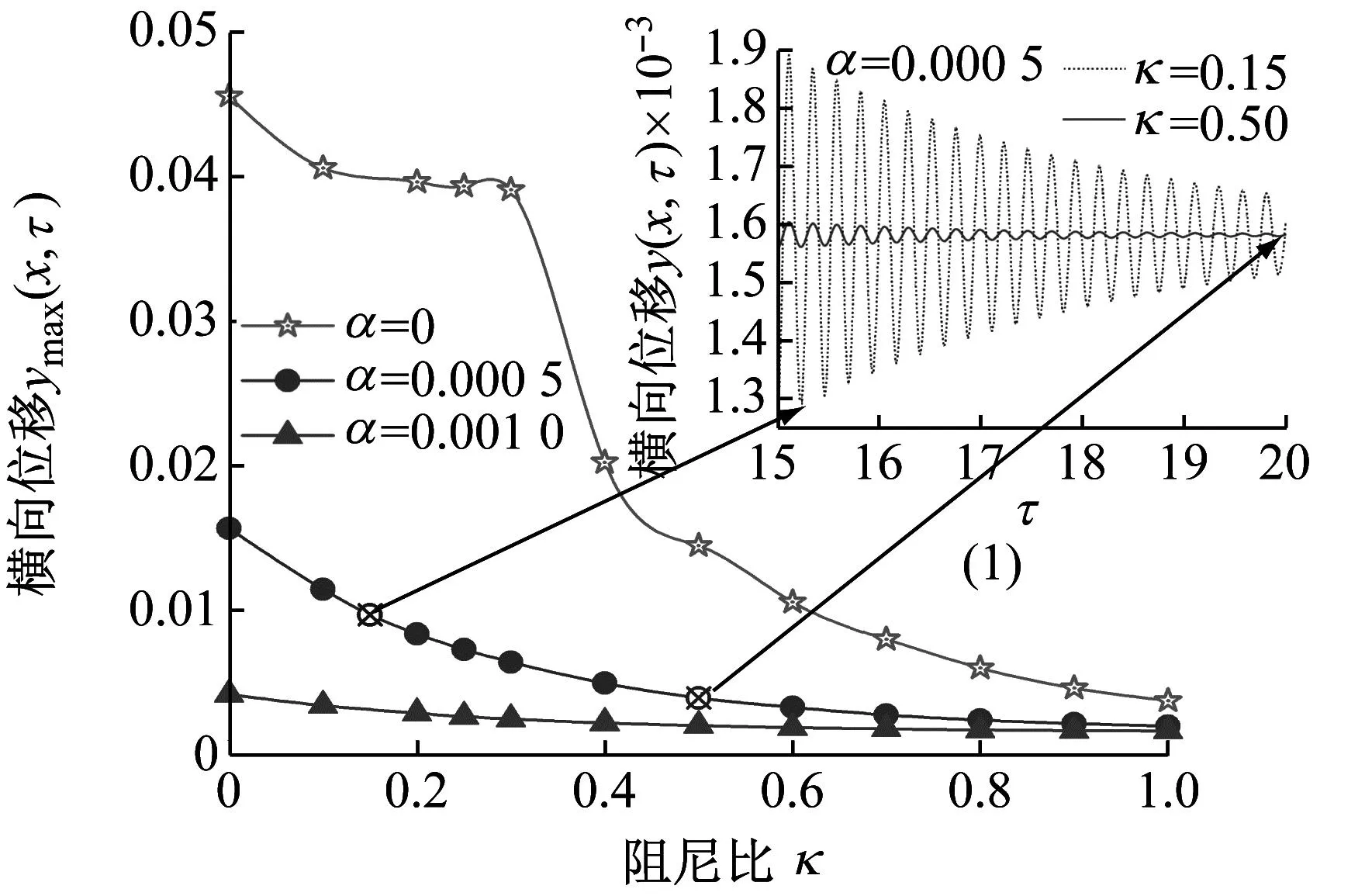
(a) C-C

4.2 线性变化的静水压力作用下管道振动特性分析

本小节研究在线性变化的静水压力作用下,内流流速和质量比对冷水管振动特性的影响,其中选定管道边界条件C-W和S-W,配重块重量为一倍管道湿重,时间τ=20,其他参数从表4中选取。图8显示了在黏弹性耗散系数α=0.01、质量比β=0.5、周围环境阻尼比κ=0和边界条件为C-W下,管道横向位移与振动频率随内流流速变化的发展规律曲线。

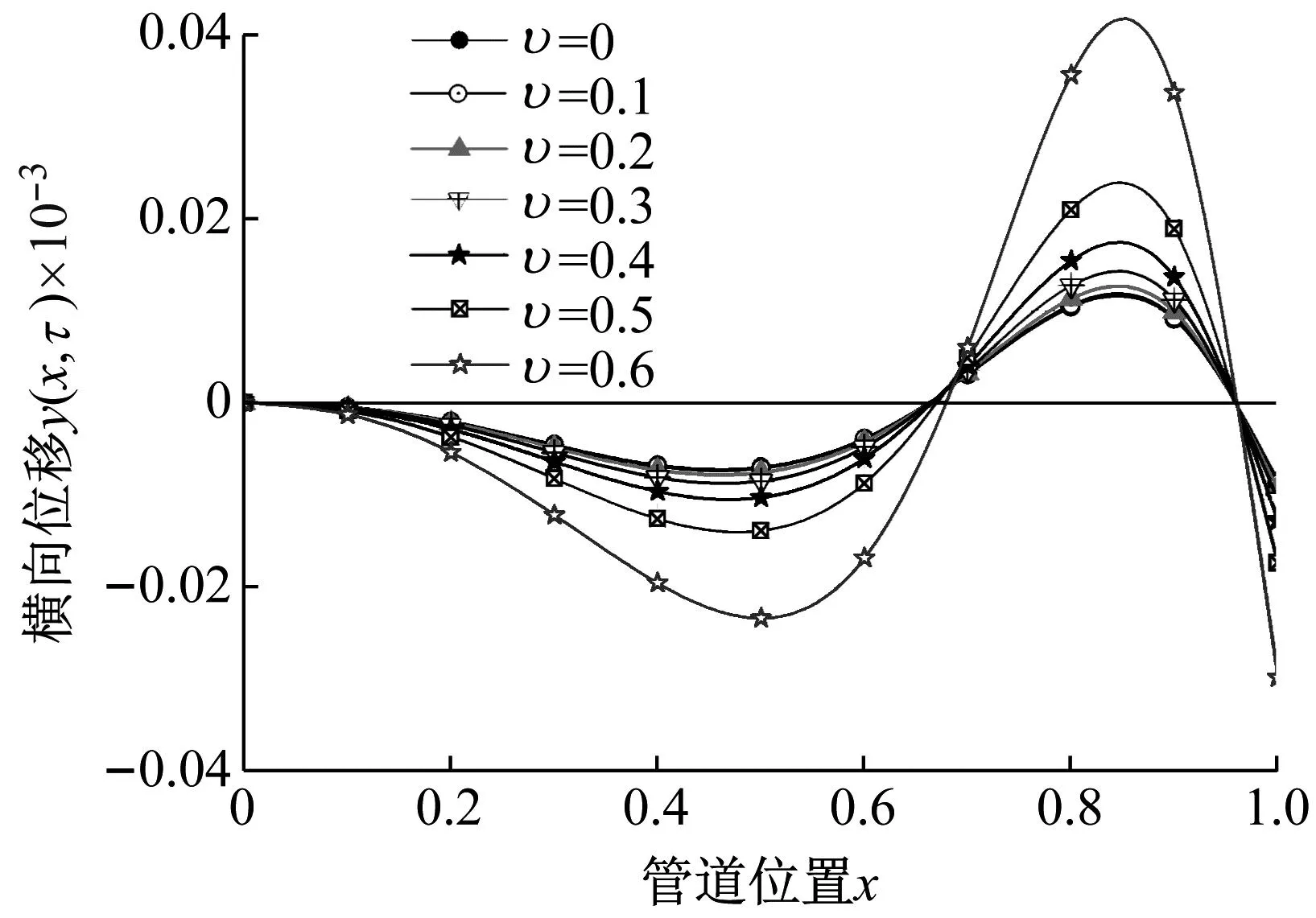
(a) 横向位移

如图8(a)为仅考虑内流流速变化时的管道横向位移发展曲线。在线性变化的静水压力作用下,管道呈现二阶振型。随着管道位置x的增大,管道横向位移呈现“S”型发展曲线。在管道底部位置(x=1.0),管道横向位移并不为零,主要原因是管道边界条件为C-W,底部约束相较于固支边界条件弱。随着内流流速的增大,管道整体横向位移呈现逐渐增大的趋势。值得注意的是,管道整体横向位移的最大值ymax(x,τ)出现在x=0.85位置处,而当υ=0.6时,管道的ymax(x,τ)发生较大的改变,这是因为在较大的无量纲内流流速和较弱的底部约束边界条件下,管道横向位移开始出现振荡现象。依据图8(b),随内流流速的增大,管道前四阶振动频率逐渐减小,管道将在曲线与零线相交点处发生失稳。不稳定性的类型具有非零实部Re(ω)和零虚部Im(ω)特点,结合GITT方法可求解得到,其临界流速υf=0.74。

进一步,图9给出了在线性变化的静水压作用下,不同周围环境阻尼比κ管道中点最大的横向位移随质量比β发展的曲线图,其中边界条件为C-W和S-W,选定无量纲内流流速为0.1,黏弹性耗散系数α=0。从图9(a)可以发现,在边界条件为C-W时,随质量比β的增大,管道横向位移ymax(0.5,τ)呈现略微减小的趋势,说明质量比β对应的惯性力对管道的响应影响较小。但增大阻尼比κ能够有效降低管道横向位移ymax(0.5,τ)。根据图9(b),边界条件为S-W,在无周围环境阻尼比κ时,随着质量比的增大,管道横向位移ymax(0.5,τ)呈现先急剧减小,对应的质量比β=0.1,后进入平滑稳定减小阶段。加入周围环境阻尼比后,管道中点最大横向位移随质量比的变化趋于稳定,进一步说明周围环境阻尼比κ相较于质量比β,更能抑制管道横向位移。总体而言,阻尼比与质量比对管道横向位移的影响是相互耦合的,若周围环境阻尼比较小,质量比应更大些,才能抑制管道在振动时的横向位移。

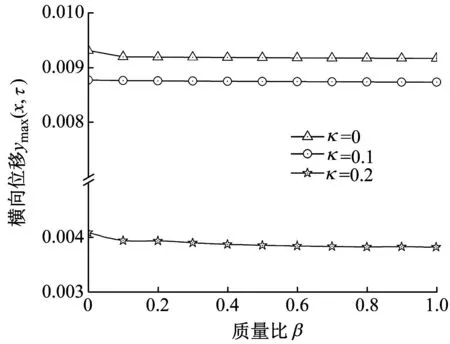
(a) C-W

4.3 集中载荷作用下管道振动特性分析

本小节研究在集中载荷作用下,内流流速、黏弹性耗散系数和激励位置对冷水管振动特性的影响,其中选定管道边界条件C-F和S-F,时间τ=20,其他参数从表4中选取。图10显示了在黏弹性耗散系数α=0.01、质量比β=0.5、周围环境阻尼比κ=0和边界条件为C-F下,管道横向位移与振动频率随内流流速变化的发展规律曲线,其中激振位置a=0.5。

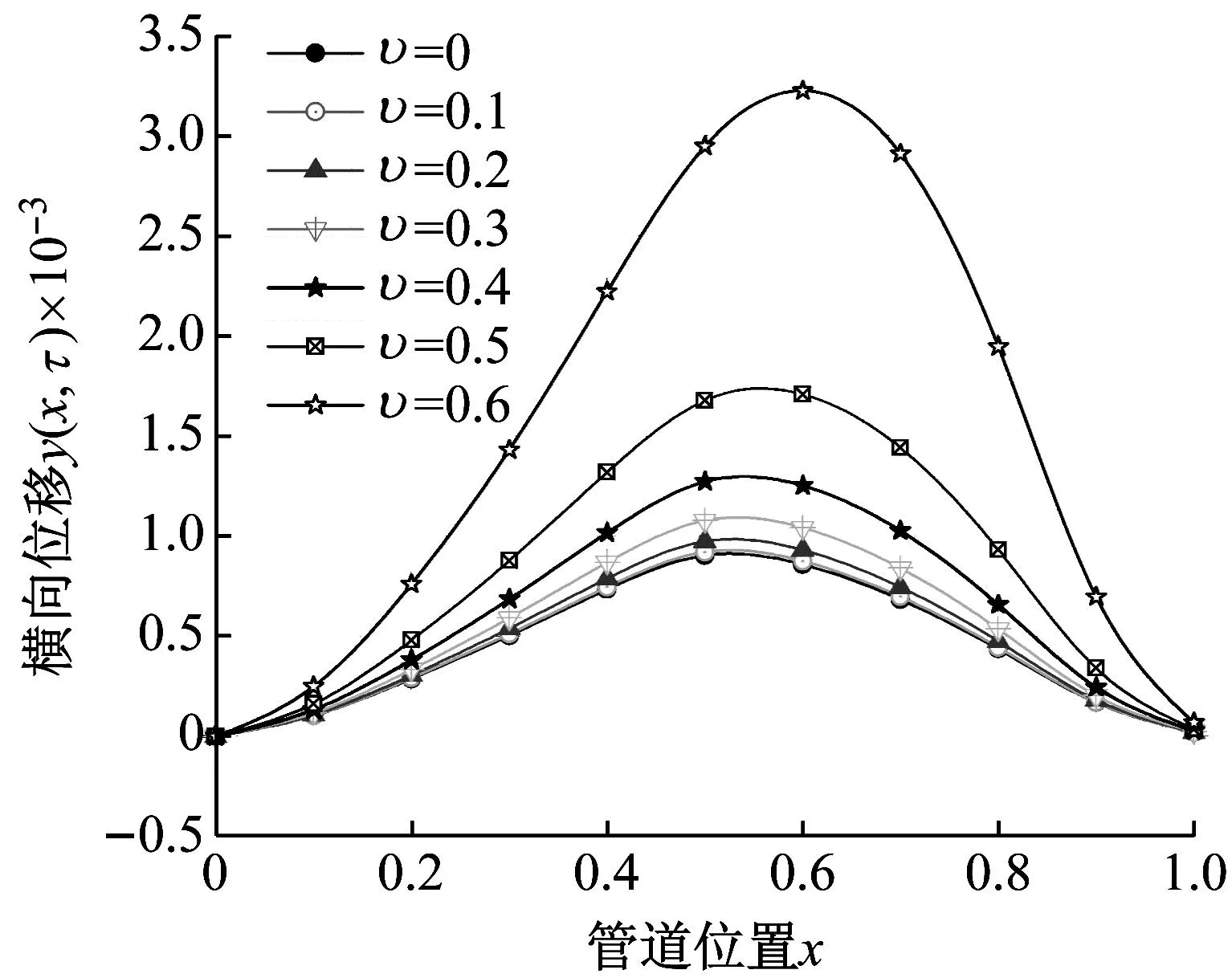
(a) 横向位移

图10(a)为仅考虑内流流速变化时的管道横向位移发展曲线。在集中载荷作用下,管道呈现一阶振型。随着管道位置x的增大,管道横向位移先增大后减小,直至为零。内流流速的增大,管道横向位移也逐渐增大,其出现最大值ymax(x,τ)时所对应的管道位置在x=0.60附近。而当υ=0.6时,管道的ymax(x,τ)相较于其他流速对应的ymax(x,τ)要大很多,对应的一阶振动频率为26.506 4。根据图10(b),随着内流流速的增大,管道前四阶振动频率呈现先增大后减小的趋势。当振动频率与此条件下的固有频率接近或相同时,管道将发生动态失稳现象。

图11显示了不同黏弹性耗散系数下管道中点最大横向位移的发展规律曲线。其中选定无量纲内流流速为0.6,质量比β=0.2,激振位置a=0.5。从图11(a)可以发现,在边界条件为C-F时,随黏弹性耗散系数α的增大,管道最大横向位移整体呈现减小的趋势。在阻尼比κ=0,0.1时,管道最大横向位移在α∈[0.1,0.2]范围内几乎不改变。当阻尼比分别为0,0.1和0.2时,管道最大横向位移急剧减小所对应的黏弹性耗散系数分别为0.4,0.3和0.2。值得注意的是,黏弹性耗散系数越大,阻尼比对管道横向位移的影响越小。根据图11(b),当边界条件为S-F时,随黏弹性耗散系数的增大,管道最大横向位移先急剧减小,后几乎不发生改变。主要原因是增大黏弹性耗散系数会引入更强的阻尼效应,降低管道横向位移,从而导致横向位移迅速减小。随着黏弹性耗散系数持续增大,使得管道材料具有更高的耗散能力,能更好地吸收引起横向位移的能量,抑制了横向位移进一步减小。

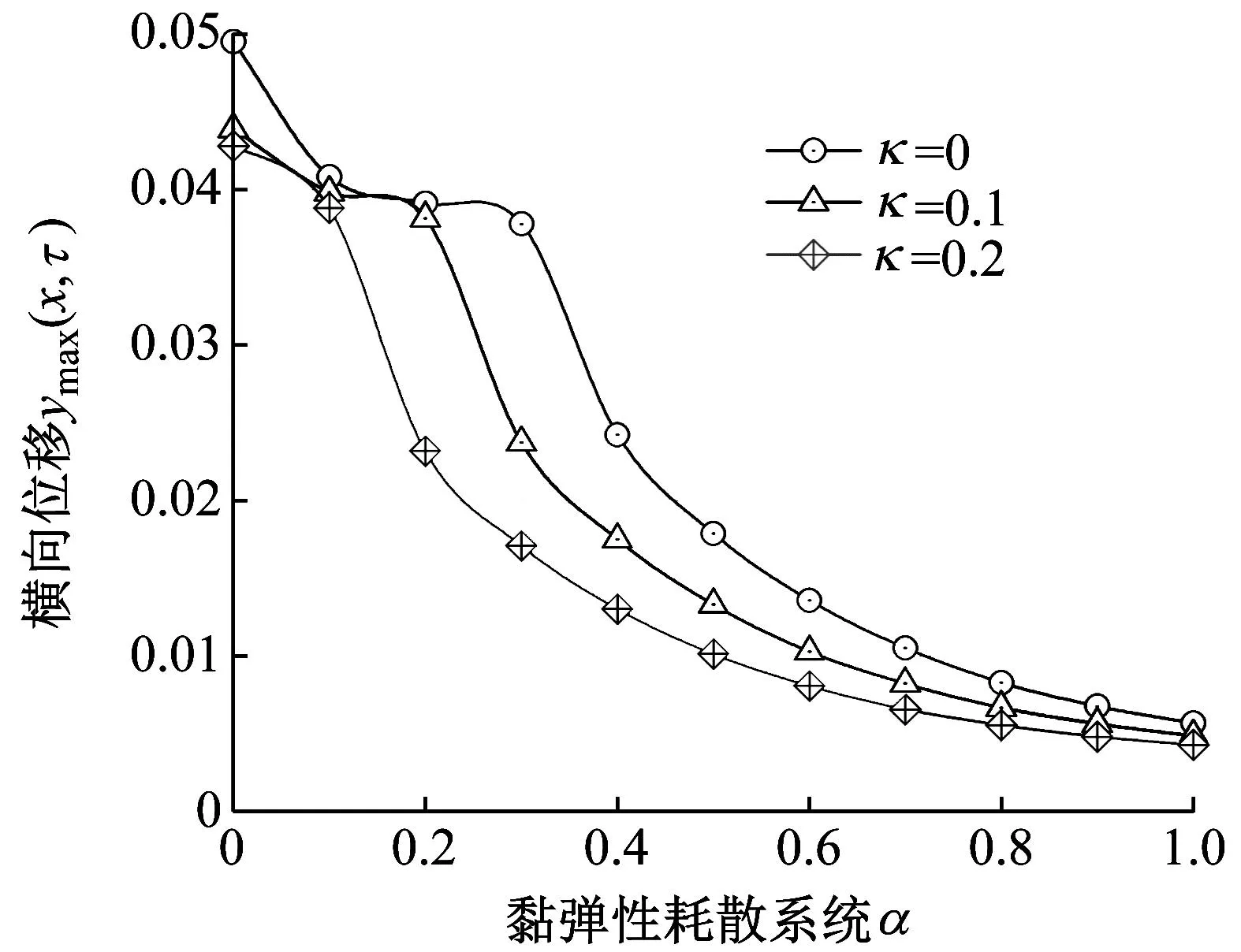
(a) C-F

为了探究集中载荷作用下激振位置对冷水管振动特性的影响,其中选取无量纲内流流速为υ=0.6,黏弹性耗散系数α=0.01、质量比β=0.5、周围环境阻尼比κ=0,图12显示了管道横向位移随激振位置的发展规律曲线。可以发现,激振位置对管道横向位移的影响十分显著。随着激振位置a的逐渐增大,管道横向位移先增大后减小,当激振位置a=0.7时,横向位移幅值ymax(x,τ)相较于其他激振位置对应的ymax(x,τ)要大。由此可知,在激振位置a=0.7附近存在一个临界值ac,使得管道在相同条件下的横向位移幅值ymax(x,τ)最大,采用GITT方法计算此条件下的理论模型,可求得ac=0.66,[ymax(x,τ)]c=0.004 16。当激振位置a继续增大时,管道横向位移呈现减小的趋势。值得注意的是,管道在集中载荷作用下,改变激振位置,管道横向位移幅值大约出现在x∈[0.20,0.75]区间内。为防止冷水管在输送超大流量的冷海水时出现动态失稳现象,应当避免管道在临界激振位置ac处的激励。

4.4 周期载荷作用下管道振动特性分析

本小节研究在周期载荷作用下,内流流速和激振频率对冷水管振动特性的影响,其中选定管道边界条件S-S,时间τ=20,其他参数从表4中选取。图13显示了在黏弹性耗散系数α=0.01、质量比β=0.5、周围环境阻尼比κ=0下,管道横向位移与振动频率随内流流速变化的发展规律曲线,其中激励位置a=0.5,激振频率ω0=4。

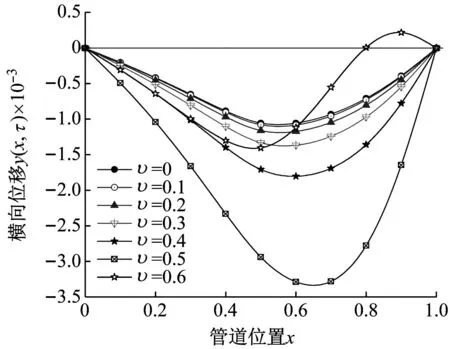
(a) 横向位移

如图13(a)可以发现,在周期载荷作用下,随内流流速的增大,管道横向位移呈现逐渐增大的趋势。在υ=0.5时,管道横向位移明显较其他内流流速对应的ymax(x,τ)大,可认为在此流速下的振动频率附近存在固有频率。值得注意的是,持续增大内流流速,当υ=0.6时,管道振型开始由一阶向二阶转变。结合图13(b),管道振动频率随内流流速的增大而减小,当振动频率具有非零实部Re(ω)和零虚部Im(ω)时,管道发生结构失稳。结合GITT方法可求解得到,其颤振速度υf=0.585。

为了探究周期载荷作用下激振频率对冷水管振动特性的影响,其中选取无量纲内流流速为υ=0.1,黏弹性耗散系数α=0.01、质量比β=0.5、周围环境阻尼比κ=0,激振位置a=0.5,图14显示了管道横向位移随激振频率的发展规律曲线。为方便读者对比计算结果,图中|yω0=4|代表在激振频率为4时,管道横向位移的绝对值。由结果分析可知,不同的激振频率对管道横向位移的作用效果明显。随激振频率ω0逐渐增大,管道横向位移呈现先减小后增大再减小的趋势。主要原因是当激振频率较小时,管道横向位移与周期载荷的相位差大于π/2,激振力对管道做负功。当管道横向位移方向发生改变时,横向位移与周期载荷的相位差小于π/2,激振力对管道做正功。因此当在激振频率ω0=12时,管道横向位移相较于其他频率所对应的ymax(x,τ)大,另一原因是此频率与管道固有频率相近导致的。

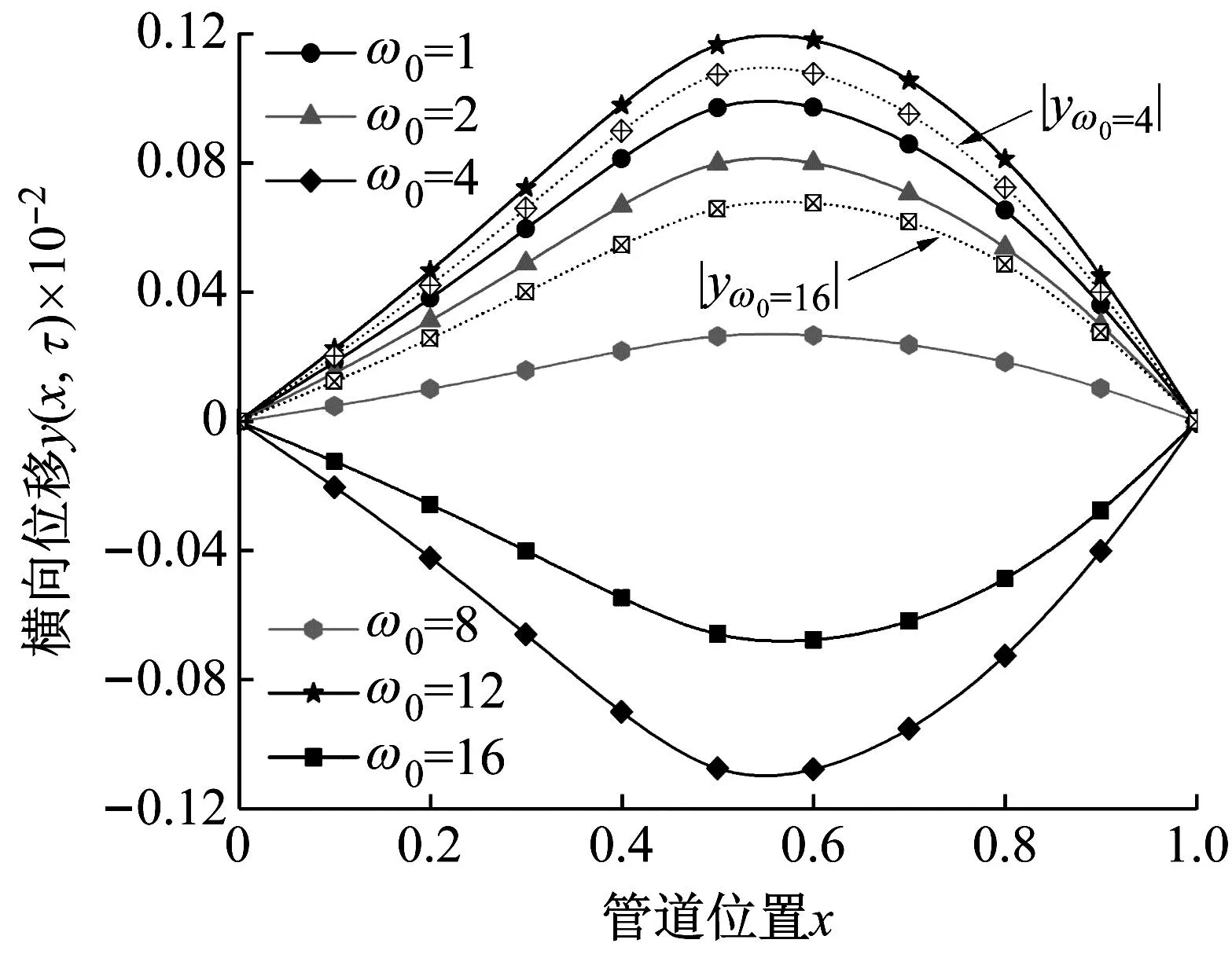
图14 周期载荷作用下冷水管横向位移与激振频率的关系曲线图(S-S)

5 结 论

本文针对海洋温差能大口径冷水管强迫振动问题,根据Euler-Bernoulli梁理论,进行了不同边界条件下冷水管强迫振动响应的理论推导,求解了相对应的特征函数与特征值。结合广义积分变换法,分析了在均布载荷、线性变化的静水压力、集中载荷和周期载荷作用下黏弹性耗散系数、质量比、周围环境阻尼比、激振位置和激励频率对冷水管振动特性的影响,得到了以下结论。

(1) 基于广义积分变换法可以得到冷水管强迫振动响应的解析表达式,与同伦摄动法(HPM)相比,求解的固有频率同等的精度,验证了理论分析的有效性。

(2) 管道在均布载荷、线性变化的静水压力和集中载荷作用下,横向位移随内流的增加而逐渐增大,振动频率呈现逐渐减小的趋势,其振型不发生改变。当内流流速对应的振动频率接近某一阶固有频率时,管体将发生动态失稳现象,此时内流流速为临界流速。而在周期载荷作用下,管道振型在较高的内流流速下将会改变。

(3) 当仅考虑单一因素的影响,管道横向位移在不同边界条件下随黏弹性耗散系数、阻尼比的增大呈现不同的发展规律,总体为减小的趋势,而质量比对横向位移几乎没有影响。综合考虑黏弹性耗散系数与阻尼比对横向位移的作用,黏弹性耗散系数的影响要大于阻尼比的影响。

(4) 随激振位置的逐渐增大,管道横向位移呈现先增大后减小的趋势。改变激振位置,管道横向位移幅值大约出现在x∈[0.20,0.75]区间内。为防止冷水管在输送超大流量的冷海水时出现动态失稳现象,应当避免管道在临界激振位置ac处的激励。激振频率对管道横向位置的作用主要取决于横向位移与周期载荷的相位差,当相位差小于π/2对管道做正功,大于π/2对管道做负功。

附录A

表A.1 6种边界条件下的特征函数与特征值