基于机器学习-网格搜索优化的砂土液化预测

王昭栋,王自法,李兆焱,苗鹏宇,吴禄源

(1.河南大学 土木建筑学院,河南 开封 475004;2.中国地震局工程力学研究所,哈尔滨 150080;3.中震科建(广东)防灾减灾研究院,广东 韶关 512026)

地震是破坏威力极强的自然灾害,砂土液化是由地震引发的主要地质灾害之一。砂土液化区域内通常会出现喷水冒砂、地面凹陷及不均匀沉降等现象,对土地和建筑造成了大面积破坏,还会对桥梁、大坝、生命线工程等造成难以预估的损失,因此寻求可靠地预测液化破坏成为岩土地震工程领域最具挑战的问题之一。

砂土液化判别方法主要有室内室外试验判别法、经验半经验公式分析方法和数值模拟判别法。张思宇等[1]基于静力触探试验数据提出双曲线模型和液化判别公式,经与国内外方法对比表明该判别公式在不同地震动强度和砂层埋深下均可给出合理判别结果。Robertson[2]通过对案例数据进行总结研究,分别从排水条件、土壤变化、抗剪强度方面对静力触探砂土液化判别公式进行了更新补充,使其更具有更广泛的适用性。王长虹等[3]以摩尔-库伦屈服准则的圆锥孔扩张理论为基础,建立了静力触探试验过程的宏细观转换公式,同时以实际案例验证了该公式对上海地区黏土或粉质黏土的适用性。

随着科学技术手段的发展,国内外专家学者以数据分析的方式研究地震构造破坏发生原因[4],也将远程遥感影像技术[5-6]和软件技术[7-9]应用至地震研究中并取得丰厚成果。此外,具备适用云计算、大数据运转及连续处理能力,且性能稳定效率更高等优点的机器学习方法也为研究人员提供了更多的思路,越来越多的研究人员开始探索机器学习-地震灾害评估研究[10-12]。李程程等[13]利用二元Logistic回归方法,以地表峰值加速度、场地平均剪切波速、复合地形指数和场地与河流的距离四个特征构建了区域性液化判别公式。姜礼涛等[14]通过收集吉林松原实例样本,建立NRS-ISSA-SVM液化判别模型,选取地下水位、地震烈度、标贯击数、非液化土层厚度4个因素作为影响因素。Kohestani等[15]以226组地震液化数据,选取液化层深度、锥尖阻力值、套筒摩擦比、有效垂直应力、竖向总应力、最大峰值加速度和震级等作为特征输入,建立随机森林模型进行预测。以上方法体现了机器学习计算迅速精确的优势,但也存在以下缺点:

(1) 影响特征选取要素比较复杂,前期准备工作耗费一定时间。

(2) 小样本的机器学习模型预测结果较好,但未能与国内及国际的传统液化判别方法进行准确率对比。

(3) 虽然名为预测模型但并未体现预测过程,未用权威的第三方数据库进行液化验证。

本文基于新西兰岩土数据库(New Zealand Geotechnical Database,NZGD)中静力触探试验报告,采用地表峰值加速度、地下水位、上覆土层厚度、液化/非液化层埋深、锥尖阻力值作为特征要素,基于Python语言构建具备液化判别、预测功能的砂土液化预测模型,使用网格搜索法对模型进行超参数优化,利用多项评价指标对模型进行性能评估,同时采用历史震害数据进行模型验证,并与国内外研究方法进行结果对比。将新西兰数据和历史震害数据集结合,通过经验分析法确定静力触探初判条件,为快速判别液化情况提供参考依据。

1 数据集准备

1.1 数据来源

新西兰岩土数据库在坎特伯雷岩土工程数据库的基础上创新开发而成,其为研究2010—2011基督城序列地震的城区灾后重建工作者提供更有效的岩土信息途径。静力触探试验(cone penetration test,CPT)是一种将探头以定速推入土壤,通过与探头相连接的传感器获得连续精确的数据并记录。因其成本较低、结果一致性及可重复性高,受到工程师及研究人员青睐。本文从新西兰岩土数据库中下载位于基督城地区519组CPT报告,提取影响砂土液化的关键因素作为砂土液化研究的数据集,试验数据来源如图1所示。

图1 新西兰震害数据来源

1.2 数据统计分析

影响液化的因素可分为动荷因素、埋藏因素及土质因素,本文根据以上三个条件共选取了5个特征。

(1) 地表峰值加速度(amax)。地震动是砂土产生液化的重要前提条件,地表峰值加速度可作为反映震动强弱的重要参数,对比图2和图3可知,基督城地区液化场地PGA区间分布为0.14～0.7g,非液化场地数据较少,PGA分布范围为0.14～0.65g。相同点是二者PGA均主要集中在0.3～0.4g之间,不同点是对于液化场地,PGA为0.4～0.7g占比24.08%,而对于非液化场地仅占比5.95%,差异显著。

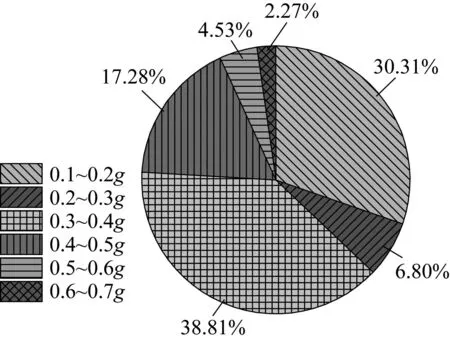
图2 液化场地地表峰值加速度特征

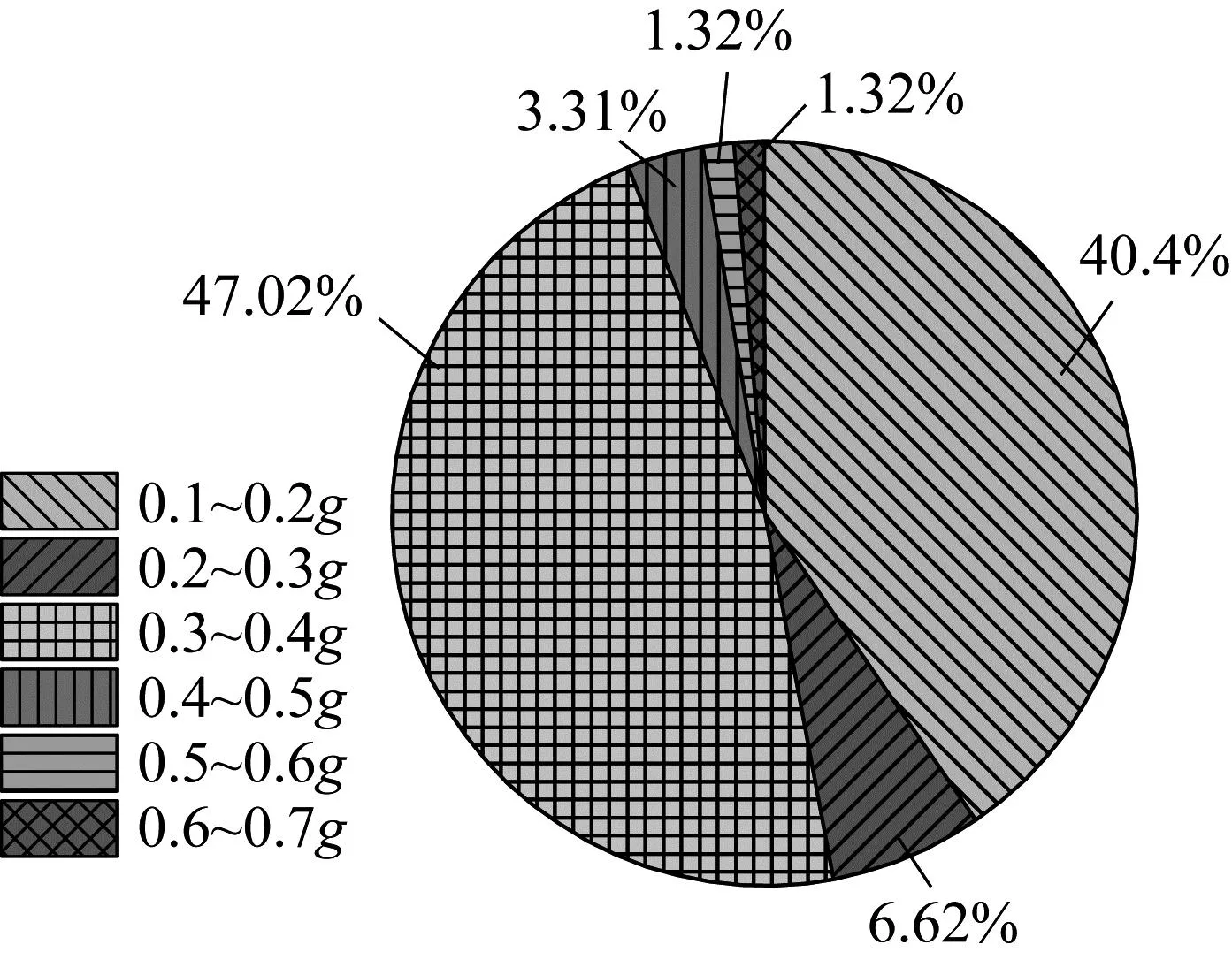
图3 非液化场地地表峰值加速度特征

(2) 地下水位(dw)。地下水位主要会影响土体的孔隙水压和抗剪强度,进而影响砂土液化能力。每一个勘察点位在静力触探报告中提供具体的地下水位数值,可直接进行提取。对比图4和图5可知,除了非液化场地存在2.41%大于6 m的地下水位,二者地下水位分布特征类似,非液化场地地下水位略低于液化场地。

图4 液化场地地下水位特征

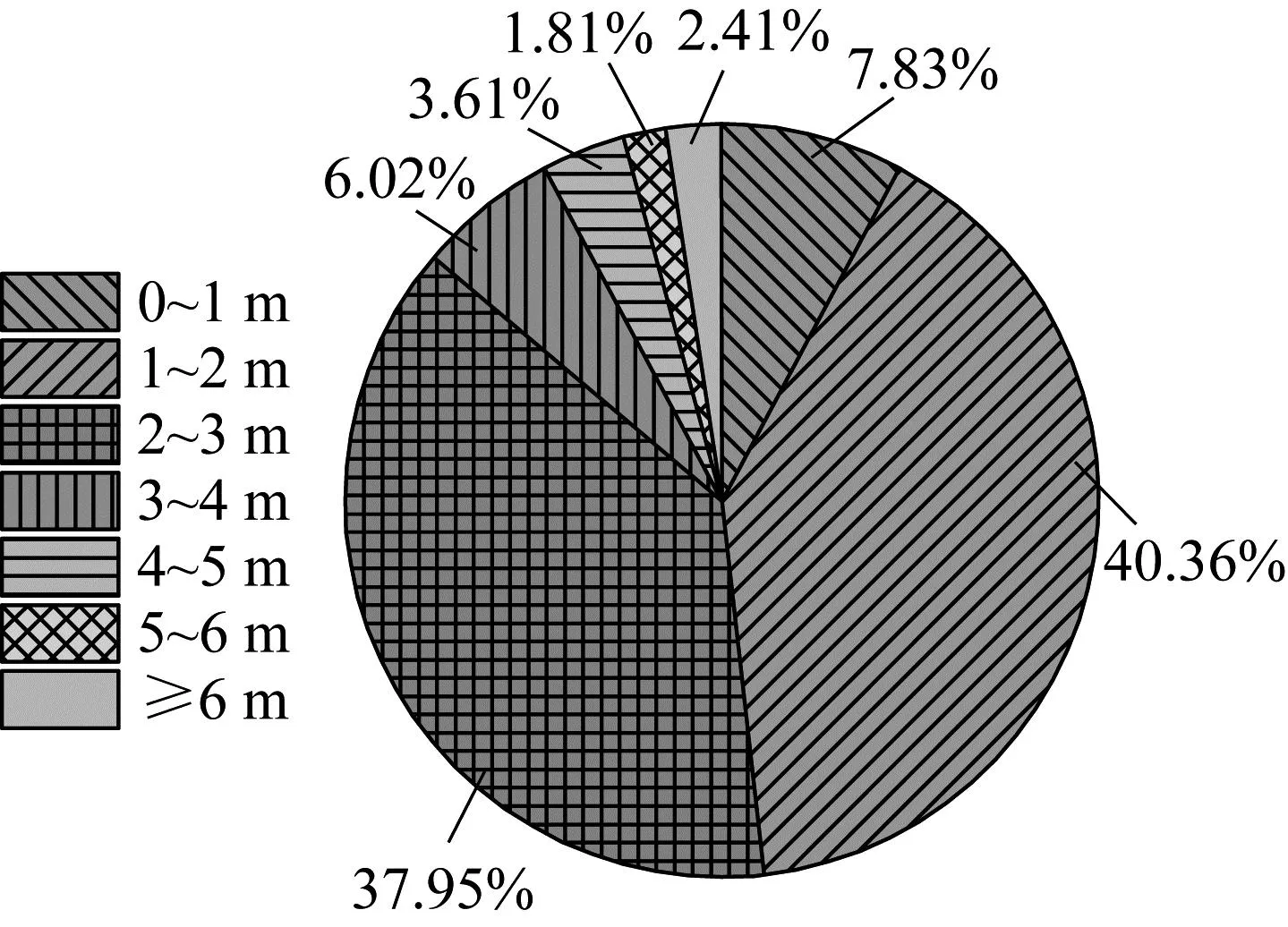
图5 非液化场地地下水位特征

(3) 上覆非液化土层厚度(du)。当上覆非液化土层厚度增加时,上覆有效应力也随之增加,其越不容易产生液化现象。经统计,液化场地的上覆土层厚度平均值为3.59,中位数为2.76,众数为2;非液化场地上覆土层厚度平均值为8.25,中位数为8,众数为6。特征差异明显,说明非液化场地的上覆土层较液化场地更厚,场地压实度更高。

(4) 液化/非液化层埋深(ds)。液化/非液化层埋深是影响砂土液化的重要因素,与勘察地点的地质条件相关。液化场地的砂层埋深分布范围为0.55～18.25 m,主要分布在3～6 m处,占比最多为48.58%,而非液化场地的砂层埋深分布范围为1.61～21.83 m,主要分布在12～15 m处,二者差异显著。对比图6和图7可知,液化场地在0～9 m处分布占比为95.46%,大于9 m的深液化层占比4.54%,为深层砂土液化提供了数据支持。

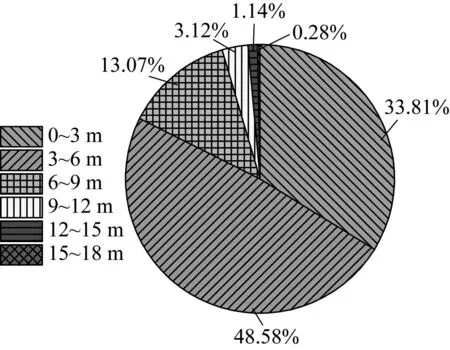
图6 液化场地砂层埋深

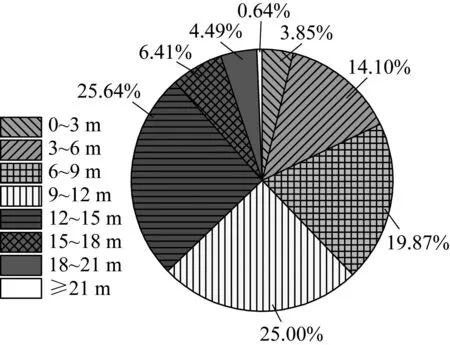
图7 非液化场地砂层埋深

(5) 锥尖阻力值(qc)。锥尖阻力值是依靠探头与土壤挤压触碰并记录实测曲线得到,其值大小反映了土壤的软硬,为确定土层液化情况提供了重要的依据。经统计,液化场地的锥尖阻力平均值为1.99,中位数为0.96,众数为0.69;非液化场地上覆土层厚度平均值为13.1,中位数为14.43,众数为15.67。特征差异明显,说明非液化场地的砂层硬度更强。

2 机器学习分类模型

本文选取三个应用较为广泛的机器学习分类模型,其中包括支持向量机、随机森林以及XGBoost,通过采用相同的性能指标评价所建立的砂土液化预测模型。

2.1 支持向量机

支持向量机(support vector machine,SVM)[16]最早由Lerner在1963年提出,是一种传统的机器学习算法。

支持向量机解决问题一般可分为线性和非线性问题两类。

2.1.1 线性问题

决策平面首先应满足约束

yi(ωxi+b)≥1-ξi,ξi≥0,i=1,2,…,k

(1)

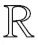
为了满足线性求解,分类函数转换为

(2)

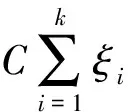
对函数进行求解需要建立拉格朗日函数

(3)

根据库恩塔克条件,得出:

(4)

(5)

至此得出线性优化问题的对偶形式,也转变成求解函数最大值问题

(6)

式中:αi为拉格朗日乘子,αi≥0,i=1,2,…,k;ω*为最优超平面的法向向量。

最终可得出相应的分类函数

(7)

2.1.2 非线性问题

对于非线性问题,支持向量机引用非线性函数,将已有样本映射至高维特征空间中,以此空间构造超平面,则目标函数为

(8)

式中,K为核函数。支持向量机中已有的核函数包括拉普拉斯核函数、高斯核函数、多项核函数、Sigmoid核函数等。

最终可得到相应的分类函数

(9)

支持向量机在求解小样本条件下的二分类问题时能力显著,可以进行硬间隔和软间隔划分,并能够在多种特征空间条件下划分出最优且唯一超平面。

2.2 随机森林

随机森林(random forest,RF)由Breiman[17]提出,它是基于Bagging基础之上创新的优秀算法,其继承了决策树“分而治之”的思想。通过以多棵分类决策树{h(X,θk),k=1,2,…,k}进行集成学习,从而得到组合分类器随机森林模型。

由于{θk,k=1,2,…,k}是独立同分布的随机变量,因此促成随机森林具备两大随机步骤,分别是Bagging思想与特征子空间思想,提升了随机森林的效率和可扩展性。随机森林单棵决策树训练过程如图8所示。

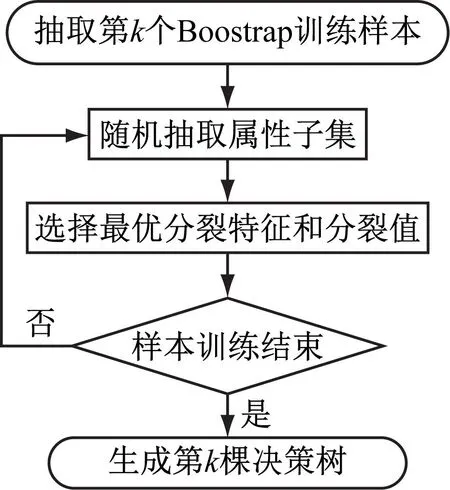
图8 随机森林第k棵决策树训练过程

通过对每棵决策树进行k轮训练,进而得到每个分类序列{h1(X),h2(X),h3(X)…,hk(X)},采用简单多数投票结果法得到最终的分类结果

(10)

式中:H(x)为汇总分类模型;hi为单棵决策树分类模型;Y为目标函数;I( )为示性函数。

2.3 XGBoost

XGBoost(eXtreme gradient boosting,XGB)由Chen等[18]提出,是Boosting算法的一种子算法,XGB同样以决策树作为基模型,在数据上建立多个弱评估器,同时通过梯度提升算法不断迭代提升形成强评估器,实现高效的分类与回归功能。

XGboost的目标函数如下所示

(11)

(12)

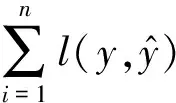
3 砂土液化预测模型

3.1 模型训练流程

Python语言是一种高效的胶水语言,其库的类别丰富,功能强大;其中,以Scikit-learn为主的库中包含了海量的机器学习方法,因此采用由Scikit-learn机器学习库导出的支持向量机(SVM)、随机森林(RF)、XGBoost(XGB)三种分类模型,在运行过程中结合了Numpy、Pandas及Matplotlab等数据分析环节,高效地完成了数据读取、数据集划分、建立模型、性能评估、可视化以及结果保存等程序,训练流程图如图9所示。

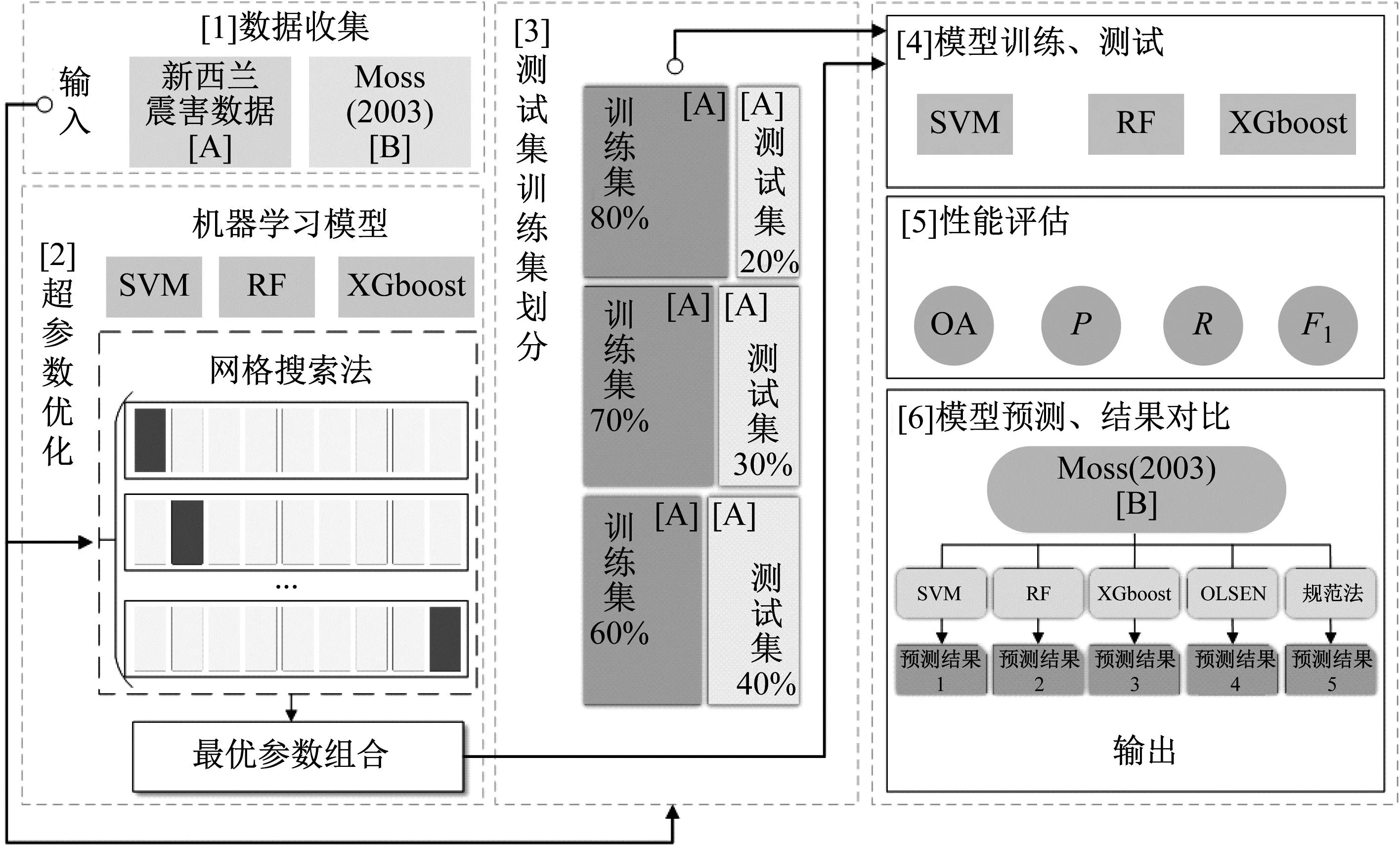
图9 砂土液化模型建立流程图

Step1:读取新西兰震害数据资料库;

Step2:对数据进行切片处理,指定模型输入特征及输出特征的类别;

Step3:调用Scikit-learn库中的SVM,RF,XGBoost函数并设置模型初始超参数,建立3种初始预测模型;

Step4:对预测模型进行训练,利用网格搜索法对3种分类模型进行超参数优化,寻找最佳超参数组合;

Step5:调整模型中训练集和数据集的所占比例,以6∶4、7∶3、8∶2对数据集进行划分;

Step6:通过超参数优化后获得最佳砂土液化预测模型,预测测试集并打分;

Step7:通过整体精度(overall accuracy,OA)、精确率P、召回率R及F1指标对模型进行性能评估,对3种预测模型综合性能进行对比分析;

Step8:利用最优预测模型对各输入特征进行重要性排序,分析排序结果;

Step9:导入Moss[19]数据,分别以机器学习模型(SVM、RF、XGBoost)、Olsen方法[20]和GB 50021—2001《岩土工程勘察规范》[21](2009版)方法进行验证;

Step10:对比验证结果,分析模型适用性。

3.2 模型建立

选取位于基督城区域内519组静力触探试验报告为基础数据库,建立砂土液化预测数据集,然后对数据进行划分,以地表峰值加速度(amax),地下水位(dw),上覆土层厚度(du),液化/非液化层埋深(ds)和锥尖阻力值(qc)作为输入特征,以液化情况(Y=液化,N=非液化)作为输出特征。由于不同的特征在量级上存在差异,因此在建立模型之前,采用式(13)对数据集进行归一化处理,使不同指标量级一致,保证数据的可运算性以及等效性。将数据集以.csv格式进行储存以后,以Pandas库中的read_csv()函数进行读取,同时,调用Scikit-learn库中的SVM、RF和XGBoost函数,分别将各影响因素导入到模型之中。

(13)

式中:Xi为各个特征中第i个样本数据;Xmax为各个特征的最大值;Xmin为各个特征的最小值。

3.3 超参数优化

超参数是调控模型性能的参数值,不同的机器学习模型内部有不同的超参数。通过搜索出最佳超参数组合并应用,进而达到增强模型的泛化能力及运算速度的效果。

超参数优化方法有随机搜索、网格搜索和贝叶斯优化三大类方法。随机搜索(random search)法是在搜索范围内随机寻找最优的超参数值,将各最优超参数进行组合,尽管运算较为迅速,但是极有可能漏掉搜索空间中重要的点进而达不到最优值。贝叶斯优化(Bayesian optimization)通过在有限空间内构造代理函数,减少了运算时间,同时运用采集函数对评估点进行精准识别,但是贝叶斯优化一旦寻求到局部极值点就会不断地在该区域内进行采样,所以很容易陷入局部最值。网格搜索(GridSearchCV)法通过采用穷举思路,在指定的参数范围内,穷尽所有的参数组合,寻求精度最高的参数,进而达到优化模型的目的。

考虑到本研究计算规模较小,所需要时间成本有限,所以可利用网格搜索法得到最佳的参数组合,达到优化模型的目的。基于Python语言引出Scikit-learn库中网络搜索法,对SVM,RF和XGBoost依次进行超参数优化,得到各个模型最优的参数值。对于关键参数最终结果如表1所示,非关键参数则采用默认数值。

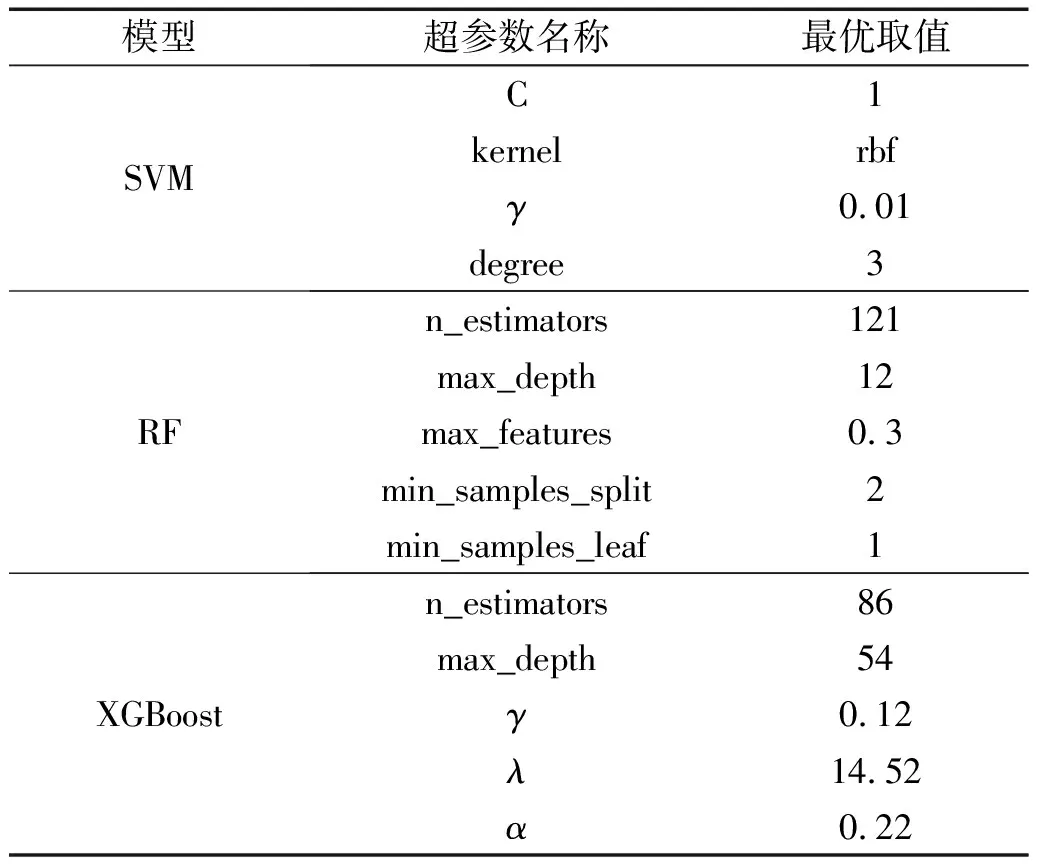
表1 基于网格搜索后的三种模型最优超参数

3.4 性能评估

本文选取了整体精度OA、精确率P、召回率R、F1值作为性能度量指标,如表2所示。OA衡量模型预测准确目标的准确率,也即正确预测的样本与所有样本的比率。精确率P衡量模型预测真阳性目标的精准度,召回率R衡量模型预测真阳性目标的完整度,因精准率P与召回率R在特定情况下不能兼顾,可采用F1指标即可综合评价考虑。

表2 预测模型评价指标

3.5 结果分析

各模型性能评价指标如表3所示。通过对比可知,在不同测试集、训练集划分下,三种机器学习分类模型得分均较高,所有值均在0.83以上,由表3分析可知,不同样本划分对模型的性能产生了影响,在训练集∶测试集=7∶3时,支持向量机和随机森林模型达到的性能得分最高,而XGB在训练集∶测试集=6∶4时达到最优值。因此,在应用多种机器学习模型时,采用不同比例的样本划分是有必要的。随机森林模型在不同比例样本划分下表现的更为稳定,各项性能指标间数值相差有限,在样本比例为7∶3时,其OA值、P值、R值、F1值分别为0.92、0.94、0.95和0.94,综合得分最高,超过在同样本比例条件下的支持向量机模型,在OA、R、F1值方面也超过在样本比例为6∶4的XGBoost模型。

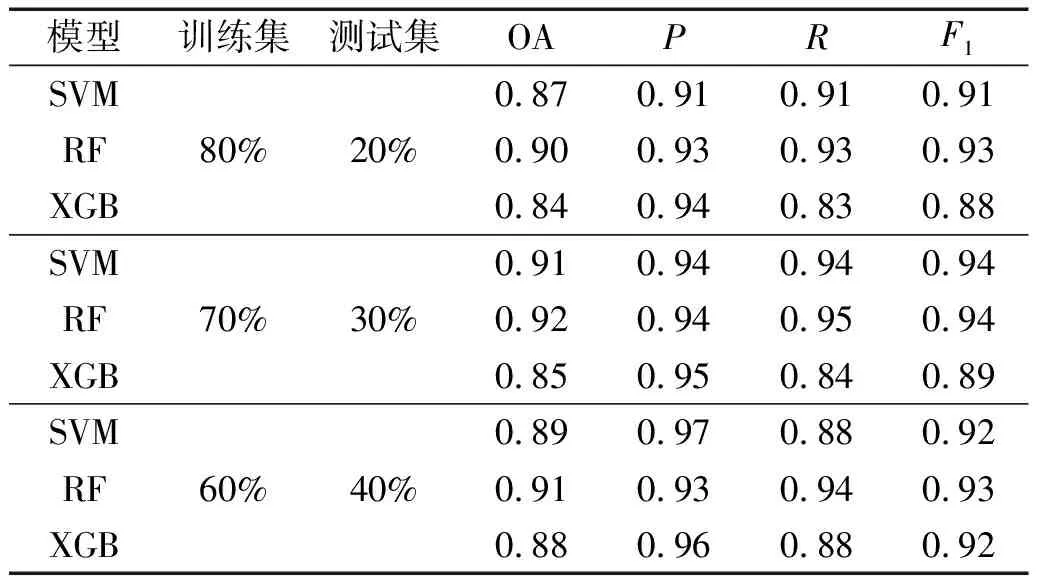
表3 性能评价指标

综合来看,相较于支持向量机与XGBoost,基于随机森林算法的砂土液化预测模型准确率最高,性能稳定且具有良好的泛化能力,总体性能排序为RF>SVM>XGBoost。

随机森林在训练数据的过程中可以检测到各个特征对分类结果的影响,特征重要性[22](feature importance)通过各影响因素进行权重打分而得到各影响因素排序,本模型选择基尼不纯度下降ΔG作为变量;置换重要性[23](permutation importance)通过打乱各变量后,计算误差变化量大小进而得出排序,其变量为个别特征重要性ij。两者的异同性如表4所示。两者计算结果如图10、图11所示。在实际分析中,可考虑将两种方法结合使用,以更全面地评估和理解特征对于机器学习模型的重要性。

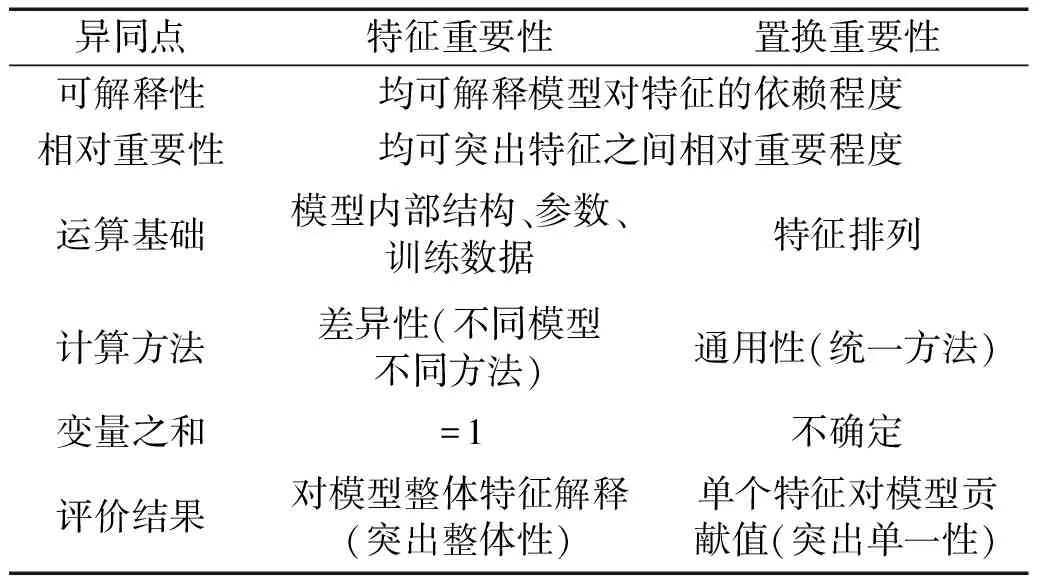
表4 特征重要性与置换重要性的异同点

图10 特征重要性排序

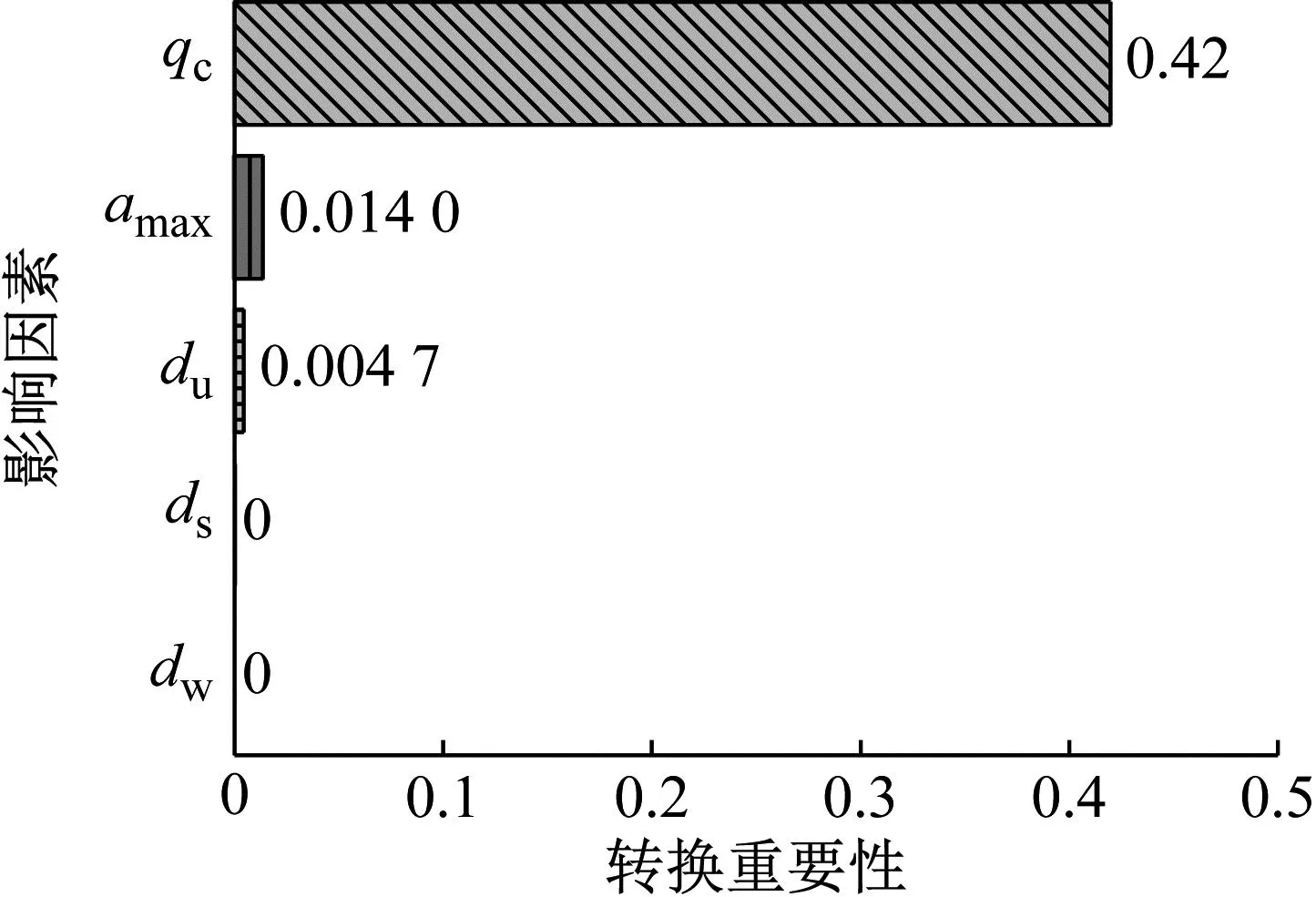
图11 置换重要性排序

由于特征重要性、置换重要性的运算过程和评价指标不同,因此所得的排序结果也存在差异。综合考虑后得出:锥尖阻力值、液化/非液化层埋深、上覆土层厚度是影响液化最重要影响因素,其中锥尖阻力值作为特征重要性与置换重要性最高值,表明是对模型影响的最关键因素,以上三个因素反映了土壤的软硬程度及砂层埋深条件,因此有理由推断土质情况是导致基督城发生液化的最主要原因,通过查文献亦可知基督城土质与Waimakariri河、Heathcote河、Avon河形成的古河道区域及其周围的沼泽区类似,这些区域地表被较新的砾石、沙子和淤泥沉积物覆盖,为产生液化现象提供了重要条件[24-28]。其次是地表峰值加速度,地震动作为砂土液化产生重要前提,是不可或缺的动荷条件,考虑到本文中基督城地区范围有限,因此特征差异性不显著。通过查询文献[29-32]可知,基督城城区的地下水位虽然随季节变化而增减,但绝大部分地区的地下水位较浅(深度为1～5 m),因此排名较为靠后。需要注意的是,因为本文考虑了选取因素的简便性,所以不代表地下水位对液化的影响是可以忽略不计的,文献[33]表明砂土导致的液化喷射沉积物与地下水压力之间存在较强的空间相关性,因此也应作为一种重要因素考虑。

4 国内外液化判别方法对比

本文选取了Moss(2003)数据库作为预测数据,将本文所建立的三种砂土液化模型、我国采用《岩土工程勘察规范》方法和国际上认可的Olsen方法五种方法进行结果对比,分析砂土液化模型的有效性。

4.1 规范法

目前我国使用最为广泛的《岩土工程勘察规范》中的国家规范法(以下简称规范法)中包含有静力触探判别方法,其主要是依据唐山地震的实际震害资料得出的液化判别公式,使用双桥试验条件下饱和土静力触探锥尖阻力临界值来做液化判别。判别表达式如下所示

qccr=qc0αwαuαp

(14)

αw=1-0.065(dw-2)

(15)

αu=1-0.05(du-2)

(16)

式中:qccr为饱和土静力触探锥尖阻力临界值,MPa;qc0为地下水位dw=2 m,上覆非液化土层厚度du=2 m时,饱和土液化判别锥尖阻力基准值,MPa;aw为水位埋深修正系数,地下常年含水且与地下水存在水利联系时取1.3;au为上覆非液化土层修正系数,深基础时取1.0;ap为土性修正系数;dw为地下水位深度,m;du为饱和液化砂土层埋深,m。

当实测锥尖阻力值qc小于饱和土静力触探锥尖阻力临界值qccr,即可判定为液化,否则判定为非液化。

4.2 Olsen方法

国际上主流的液化判别方法是循环剪应力比法,即土体在地震条件下产生的循环应力比(cyclic stress ratio,CSR)与相应动力条件下土体的抗液化应力比(cyclic resistance ratio,CRR)作数值比较。当CSR>CRR判别为液化,否则判定为非液化。CSR的计算公式为

(17)

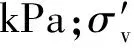
1996年美国NCEER(National Center for Earthquake Engineering Research)专家组认可了基于CPT的Olsen判别方法,Olsen方法适用于所有土类情况,是一种使用更为广泛的方法,其判别式为

(18)

(19)

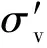
4.3 历史震害数据统计分析

Moss(2003)总结了从1964—1999年这35年中,世界各地共发生的19次地震砂土液化事件,数据全面、详细且置信度高。

将历史震害数据按照液化/非液化点区分,其中液化点139个,非液化点43个。绘制多Y轴柱状图可以直观对比各烈度区内特征均值的变化情况,组内的误差棒也反映了数据的偏离情况。按照现行GB/T-17742—2020《中国地震烈度表》[34]进行烈度划分,对比图12和图13可知,液化点与非液化点的大部分特征基本呈现随烈度区增加而增加的现象,对于地表峰值加速度,汇总统计知液化点以0.25g和0.4g最多,非液化点以0.17g最多,但两者的均值在烈度区内差别不大。对于地下水位,由图12和13可知,非液化区域的地下水位明显低于液化区域的地下水位值,液化点集中在1～2 m,非液化点集中在2～3 m,因此均值差别较大,且由误差棒知该特征的离散程度最大。上覆土层厚度与液化/非液化层埋深是所收集的五个影响因素中,液化/非液化点差别最不明显的两个特征,在各烈度区内基本呈现一致变化。锥尖阻力值的差距最为明显,基本上非液化点的锥尖阻力均值为液化点均值的两倍。

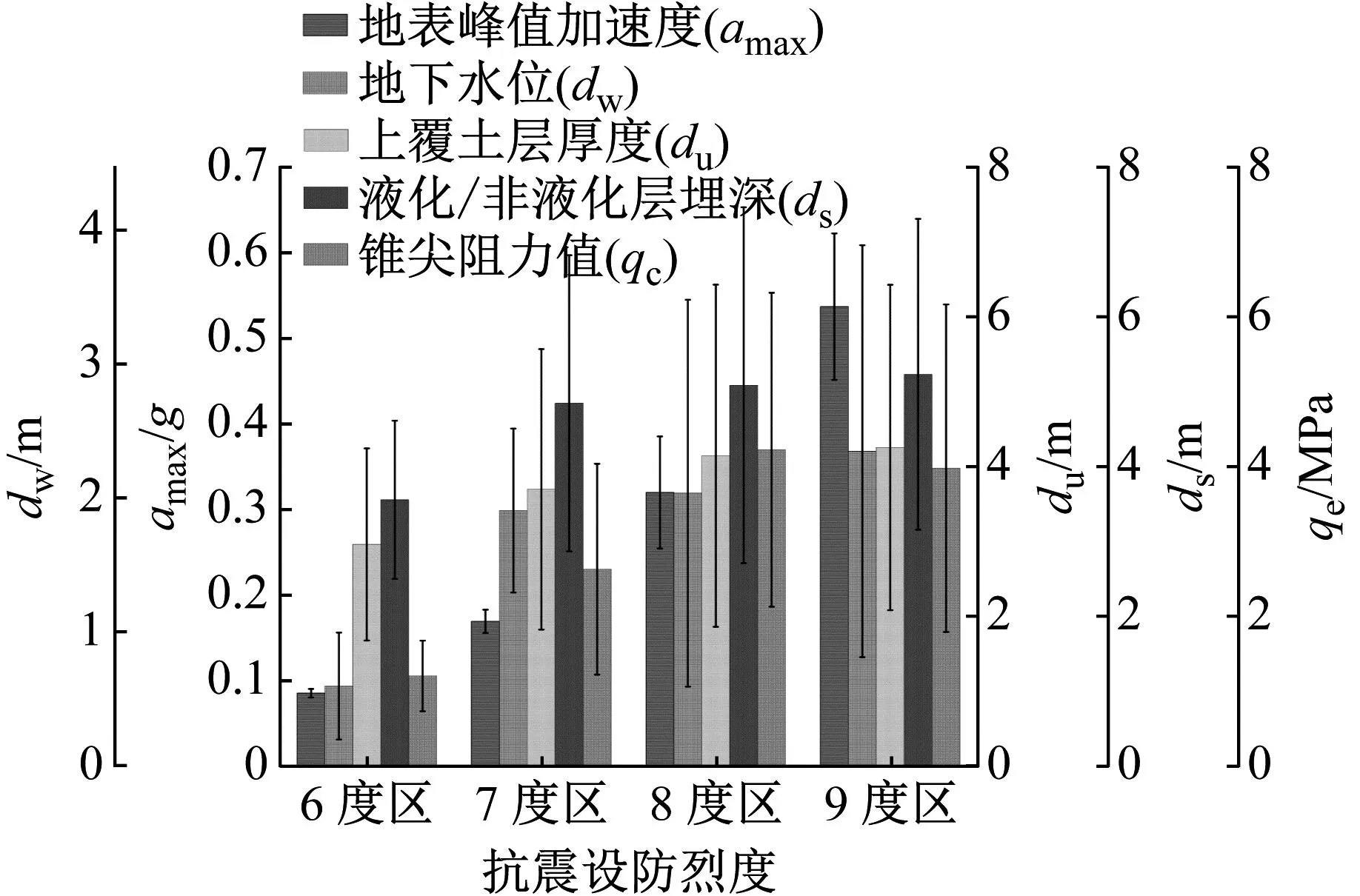
图12 历史震害数据集液化点特征分布

图13 历史震害数据集非液化点特征分布

矩阵散点图可以快速发现成对变量之间的关系,通过矩阵图中的箱线图可知,地表峰值加速度、地下水位、上覆土层厚度、液化/非液化层埋深与锥尖阻力值的中位数分别为0.28g、2 m、3.4 m、4.45 m和3.9 MPa,同时,可以发现地下水位和锥尖阻力值存在较多异常值,说明历史震害数据集中各地的地下水位置和土质软硬程度区别较大。同时引用皮尔逊相关性系数进行数据分析,其主要描述了两个变量之间线性相关强弱的程度。由图14具体的相关数值可知,上覆土层厚度与液化/非液化层埋深呈现高度线性相关,地下水位与上覆土层厚度呈现显著线性相关,地下水位与液化/非液化层埋深呈现低度线性相关,其余特征之间不存在线性相关性。

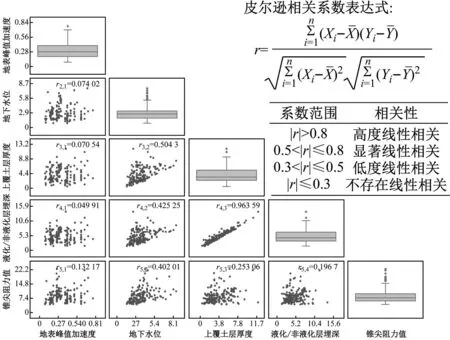
图14 皮尔逊相关性分析

4.4 验证结果对比

为了使计算更为系统、迅速,基于Python语言写入了Olsen方法以及规范法判别公式。将已储存完成的历史震害数据导入到公式中进行判别并得到结果,以此进行传统液化公式的准确率计算。

同时,将以新西兰震害数据建立好的砂土液化预测模型,将SVM和RF的样本比例划分为7∶3,将XGboost样本比例划分为6∶4,使模型具备最佳超参数组合与最佳样本比,引用.predict()函数进行验证历史震害数据并记录,统计砂土液化预测模型的准确率,最终三种方法预测结果准确率如表5所示。

表5 液化验证准确率对比

在与机器学习方法对比时,随机森林准确率最高,且在各烈度区的准确率均超过支持向量机与XGBoost,其次是XGBoost模型,液化判别准确率略低于随机森林,但仍超过规范法与Olsen方法,对于非液化点判别准确率较低。支持向量机模型对于历史震害数据库验证准确率最低,证明了基于决策树方法建立的模型对分类问题的优势。

通过与国内外判别方法对比,随机森林方法在液化点判断准确率均较高且稳定,总体正确率为97.5%,为三种方法最高,在非液化点准确率为38.25%,高出Olsen方法6%左右,非常接近于规范法,证明随机森林模型能够达到与二者权威方法接近的准确率。此外,相较于无法判断6度区液化情况的国家规范法,随机森林模型适用范围更为广泛,准确率较Olsen方法更高。本文选取地震动峰值加速度、地下水位、上覆土层厚度、液化/非液化层埋深、锥尖阻力值作为特征要素,简单易求,计算迅速,适用于动态数据及大数据运算,可作为一种良好的液化判别模型。值得注意的是,作为国际上通用的Olsen方法在判别8、9度区非液化点时准确率分别为6%和0%,判别过于保守,基本上不具备非液化判别能力,若以此结果进行布置抗液化工程则是不符合实际的。

5 静力触探判别的初判条件

5.1 锥尖阻力阈值的确定

通过参考GB 50011—2010/《建筑抗震设计规范》[35]中采用上覆非液化土层厚度和地下水位深度两因素确定的液化初判公式,本文提出基于新西兰震害数据、历史震害数据和李兆焱等[36]的数据组成的734组新数据库的静力触探初判条件(以下简称初判条件),即确定了在砂层埋深限制下锥尖阻力阈值。通过砂层埋深与锥尖阻力阈值即可快速判别液化情况,将 CPT进行烈度划分如图15～图17所示,得出锥尖阻力阈值表如表6所示。

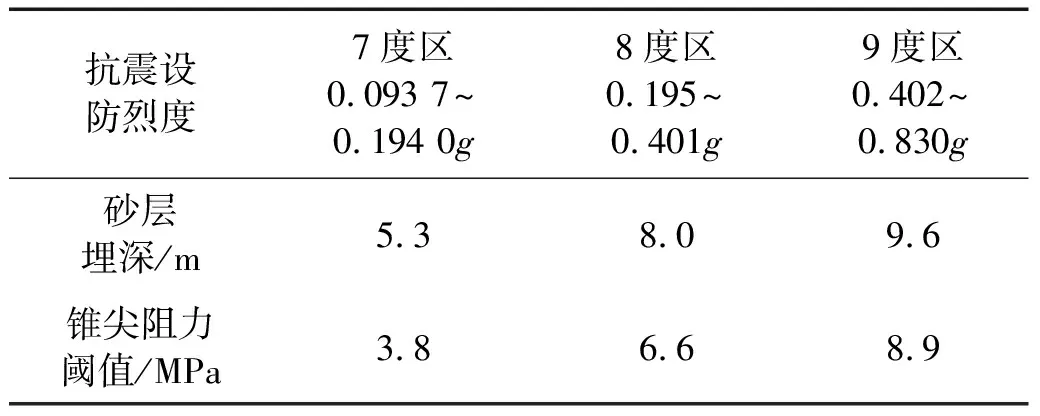
表6 锥尖阻力阈值表(仅适用于饱和砂土或粉土)

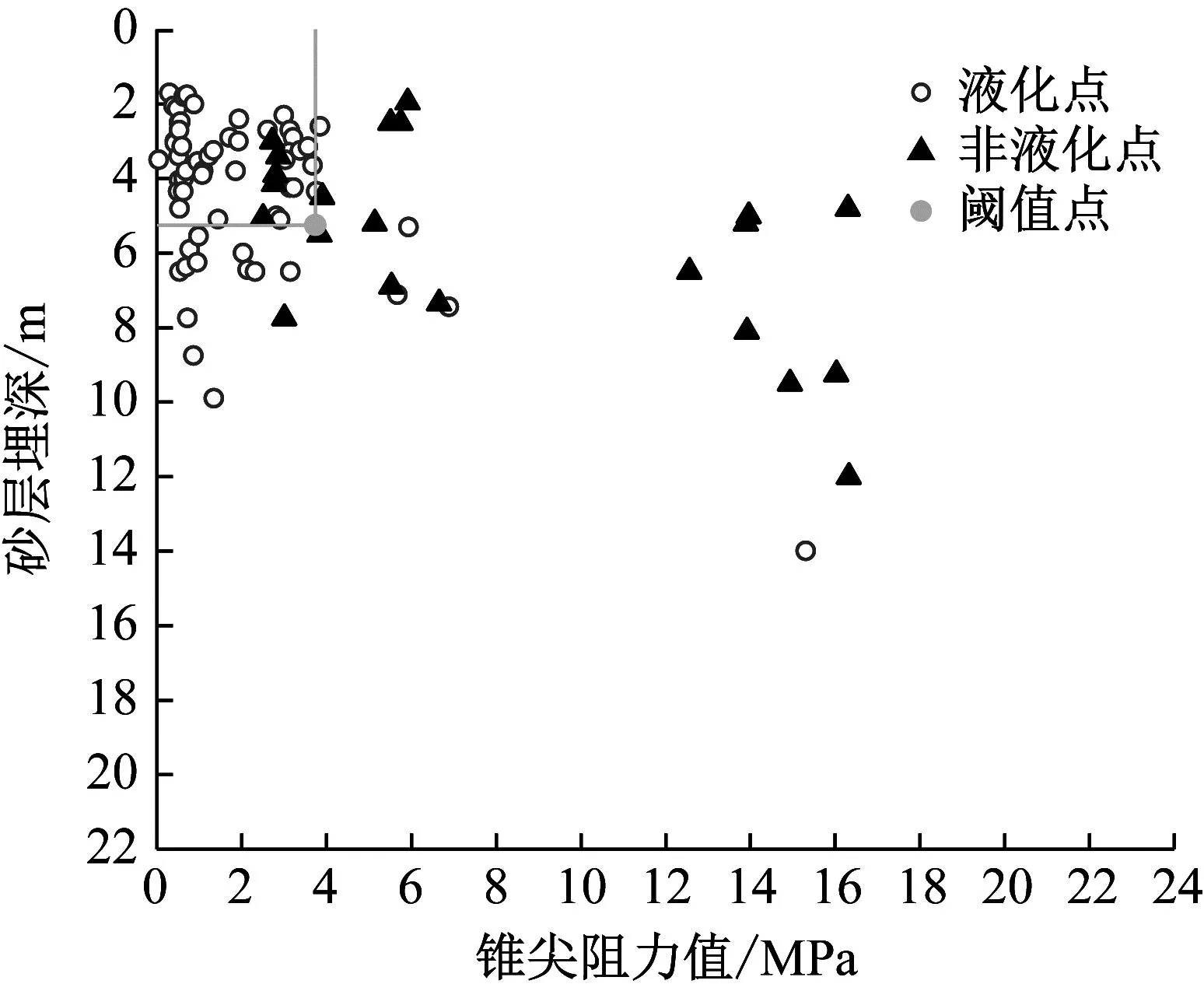
图15 7烈度区阈值点分布

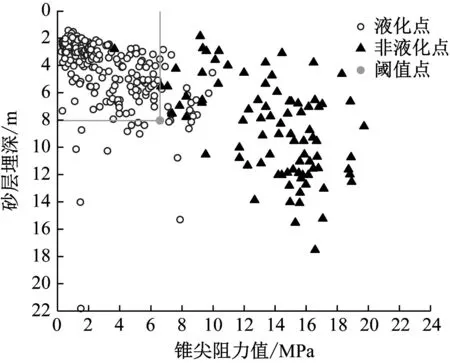
图16 8烈度区阈值点分布

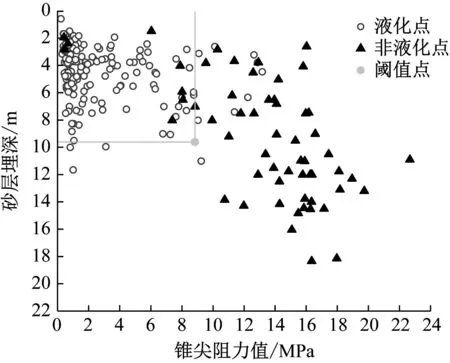
图17 9烈度区阈值点分布

5.2 与规范法对比

通过与我国采用的规范法进行对比,选取新数据库中的液化点作为验证集,二者判断液化的准确率如表7所示。经检验,初判条件在7度区、8度区、9度区的准确率分别为90%、98%和97%,与规范法各烈度区准确率接近,总体准确率与规范法相同。相比于基于唐山地震数据确定的规范法,初判条件可以作为一种更好的液化初判方法,优势如下:①基于世界各地震害资料而建立,可信度更高,适用范围更广;②所考虑参数条件少且无需进行公式判别;③可解释性强。

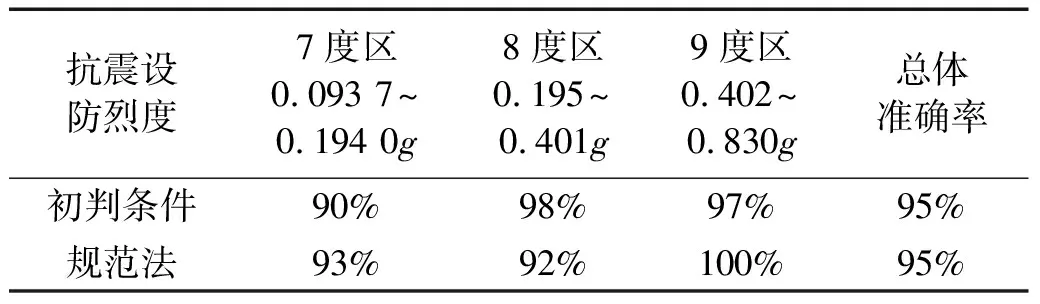
表7 液化判别准确率对比(仅液化点)

6 结 论

本文基于新西兰地震液化数据,建立了可进行液化判别及预测功能的随机森林模型,通过研究得出以下结论:

(1) 通过对新西兰震害数据进行训练、测试及性能评估后得知,随机森林整体精度为0.92、精确率为0.94、召回率为0.95、F1值为0.94,为三种分类模型中性能最优的模型,说明随机森林模型对数据的拟合及泛化能力较强,其次是XGBoost模型,最后是支持向量机模型。

(2) 选取了地震峰值加速度、地下水位、上覆土层厚度、液化/非液化层埋深、锥尖阻力值作为影响因素,分别代表动荷条件、埋藏条件及土质条件三大砂土液化前提。经过影响因素排序及阅读文献验证可知,基督城地区产生地震液化的重要原因在于土质要素,其中以代表着土壤软硬程度的锥尖阻力值特征为地震砂土液化的最主要原因。

(3) 将建立的模型使用Moss(2003)数据集进行验证,通过与支持向量机、XGBoost、规范法、Olsen方法等方法进行预测结果对比可知,随机森林模型在液化点判别总体准确率为97.5%,为五种方法中判别精度最高的方法,在非液化点判别总体准确率为38.25%,高出Olsen判别方法6%左右,非常接近于规范法。因此,相比于无法进行6度区判断的规范法和非液化点判别准确率较低的Olsen方法,随机森林适用范围广泛,要素简单易取、计算迅速,避免了烈度划分及复杂因素计算等诸多限制条件,证明了随机森林模型在液化判别预测方向的可适用性及其优越性。

(4) 基于详实的历史液化震害资料得出不同烈度区的锥尖阻力阈值,通过与规范法进行验证对比可知,静力触探初判条件具有准确率高、可适用性广、无需计算等优点,可以作为一种准确快速的液化初判方法。

致谢

感谢新西兰岩土工程数据库为本文提供数据支持。