大跨度公铁两用双层钢桁桥涡激振动控制研究

陈天瑀,马存明,段青松,向鸿鑫

(1.西南交通大学 土木工程学院,成都 610031;2.风工程四川省重点实验室,成都 610031;3.西南科技大学 土木工程与建筑学院,四川 绵阳 621002)

近年来,由于桥梁的跨度逐渐增加,直接导致风致敏感性增强,所以大跨度桥梁的风致振动就成为桥梁建设中的一个关键性问题。涡激振动是一种流-固耦合现象,同时具有自激和强迫两种特性,由主梁或防撞栏杆、检修轨道等其他构件产生的交替脱落的旋涡引起。随着风速的增加,当旋涡的脱落频率与主梁的某阶模态频率吻合时,则会导致主梁出现幅度有限的振动,而主梁的振动又会反过来影响旋涡的脱落,出现锁定、稳定分支等非线性气动现象。主梁涡振响应的锁定风速区间和幅值大小主要受到断面气动外形、来流特性以及结构动力特性等因素的影响[1-2]。

近年来,大多数针对桥梁主梁涡激振动的研究都集中在箱梁上[3-5],关于桁架梁的涡振响应研究比较少。桁架梁由上弦杆、下弦杆、腹杆以及其他构件组成,不同构件会表现出不同的钝体气动特性,会产生大小不一、脱落频率也不同的尾流,使得桁架梁的涡振响应复杂化。此外,桁架梁部分构件之间的距离沿主梁展向变化,导致气动干扰变得更加复杂。Oh等[6]提出了一种预测公铁两用桁架桥涡激振动起振风速的方法。Chen等[7]发现双层公路桁架桥的竖向涡振可能是由上层桥面防撞栏杆所产生的尾流导致的,扭转涡振可能与下层桥面产生的尾流有关。与箱梁相比,桁架梁的涡振性能更难评估并且尚未得到充分的探索,需要进一步研究。

当前提高大跨度桥梁抗风能力的措施通常包括机械措施和流动控制措施。机械措施主要是通过采用一些设备增加结构的刚度、阻尼或适当增加一定质量的重物来降低桥梁的风致振动响应[8-9]。流动控制方法从是否需要附加能量输入的角度来看又可以分为两大类:主动控制和被动控制[10]。主动控制方法是通过将附加的能量引入流动,从而产生并保持控制效果,它可以根据该桥振动的实际情况有针对性地调整相关参数,从而达到最优的涡振控制效果。然而,如果要实现可调控地输入附加能量,就会增加桥梁整体系统的复杂性,相应的成本也会大幅提高。目前桥梁主动控制主要的实现形式有等离子体控制[11]、主动吸吹气[12-13]以及合成射流[14]等方法。被动控制方法不依赖额外的能量输入,主要是通过改变主梁断面的形状或表面特征等方式来改变原有的流场,从而实现涡振控制,如导流板[15]、风嘴[16]、中央稳定板[17]等。而且由于这种方法不需要附加的能量输入,所以其结构比较简单、成本相对较低,在设计工况下具有良好的控制效果。

本文以主跨为988 m的公铁两用双层桁架桥为工程背景,通过1∶58.6的节段模型进行风洞试验获得主梁断面涡振性能,并在此基础上进行计算流体动力学(computational fluid dynamics,CFD)数值模拟,研究该主梁发生涡振的原因,之后针对性地设置气动措施,提出了一种波浪形风嘴的三维被动控制措施,并研究了其几何参数对控制效果的影响,最后通过风洞试验验证并比较了各种措施的有效性。

1 工程概况

该桥是一座主跨为988.0 m的斜拉-悬索协作体系桥梁,该桥主梁采用两片主桁结构,桁式采用三角桁,桁高为 13.5 m,桁宽35.0 m,宽高比为2.59,主梁上层与下层桥面皆采用正交异性整体钢桥面板、密横梁体系。相比山区的桥梁,该桥横跨长江,均匀的来流对桥梁的涡振性能更加不利。桁架桥总体布置图、成桥状态主梁断面示意图,如图1、2所示。实桥结构的主要参数与节段模型的主要参数之间对应关系,如表1所示。

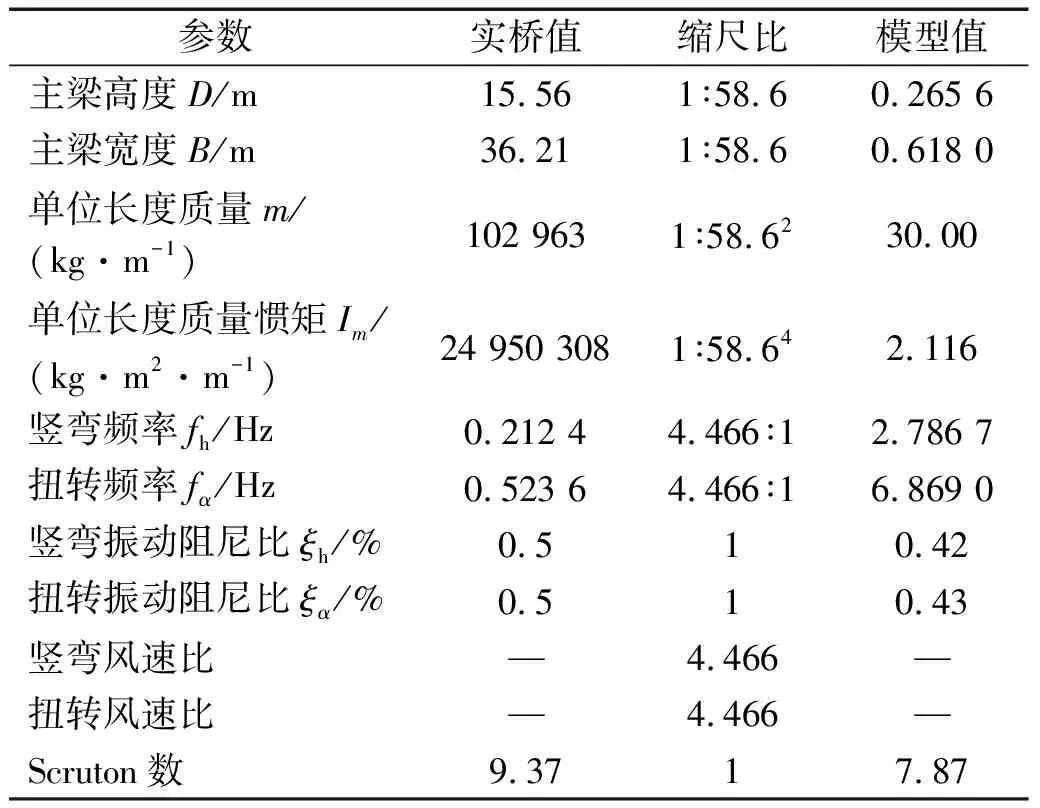
表1 成桥状态实桥与模型参数

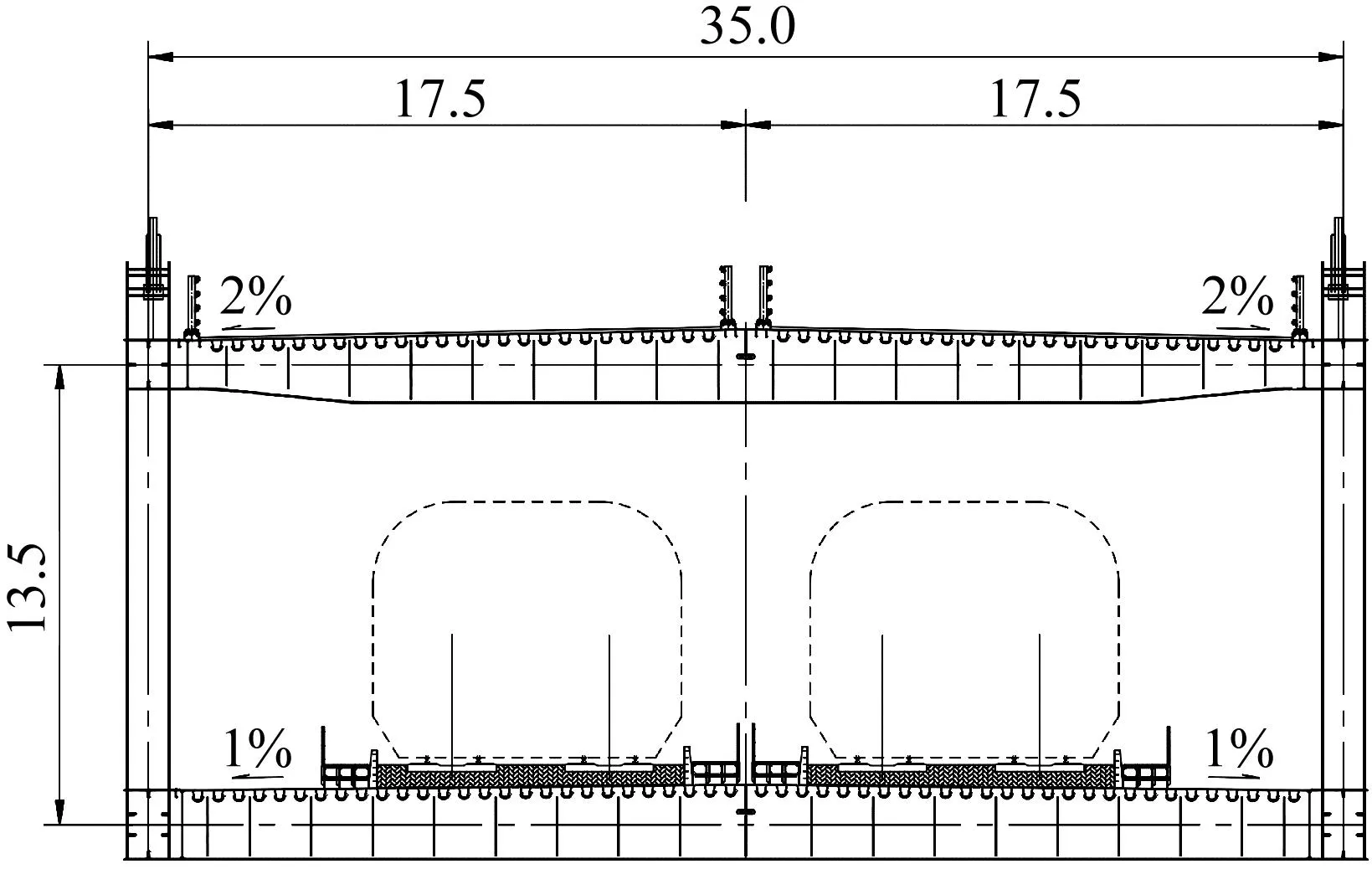
图2 成桥态主梁断面示意图(m)

2 原始断面涡振性能研究

2.1 模型及试验设备

本次试验在XNJD-1回流串联风洞的第二试验段中进行,此试验段宽2.4 m,高2.0 m,风洞内的紊流强度小于1.0%,可以很好地模拟均匀流条件。主梁节段模型采用1∶58.6的几何缩尺比,模型长L=2.095 0 m,宽B=0.617 9 m,高D=0.265 6 m,长宽比L/B=3.39,模型与实桥之间除要满足几何外形相似外,还满足了弹性参数、惯性参数和阻尼参数的一致性条件。模型材料采用ABS(acrylonitrile butadiene styrene)塑料和铝板,桥面系采用ABS塑料板整体雕刻制作,为了增加模型刚度,桁架弦杆与腹杆按图纸缩尺尺寸采用铝板整体切割制成。在模型的前方布置了Cobra风速仪,用于试验来流风速的测量。在模型的几何中心位置和背风侧边缘处分别布置了1个激光位移计。节段模型通过悬臂支架与8根位于洞外的拉伸弹簧组成的悬挂系统安装于风洞之中,保证模型可以发生竖弯和扭转振动,使用1.00 m×0.56 m的端板保证节段模型的二元流动,节段模型如图3所示。

图3 节段试验模型

2.2 试验结果

涡激振动节段模型风洞试验分别在α=0°、+3°、-3°三种攻角条件下进行。试验在均匀流场中进行。对于每一个工况,试验风速范围为0～25 m/s,在找到其涡振区后,风速再按0.1 m/s递增,以确定准确的涡激振动起始风速和最大振幅。节段模型无量纲竖向位移和无量纲扭转角位移,如图4、5所示。

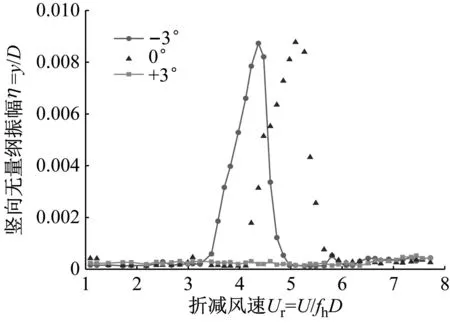
图4 原始断面主梁竖向涡振响应

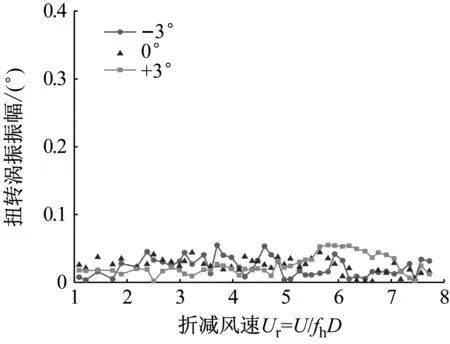
图5 原始断面主梁扭转涡振响应

试验结果表明:主梁节段模型在α=+3°攻角下未发生涡激振动现象,在α=0°、-3°攻角下均发生了明显的竖向涡激振动现象,0°攻角下主要涡振区间位于3.7～4.6的折减风速范围内,当折减风速Ur=4.4时,涡振最大竖向无量纲振幅为0.008 7;-3°攻角下涡振振幅最大,主要涡振区间处于4.4～5.5的折减风速范围内,当折减风速Ur=5.1时,涡振竖向无量纲振幅达到最大值0.008 8。上述两个角度的卓越频率成分明显,涡振锁定区间内的卓越频率为2.812 5 Hz,与结构固有竖向频率2.786 7 Hz接近,出现了锁定现象。但在0～25 m/s的常遇风速区间内,各个风攻角下均未发生明显的扭转涡激振动。

3 桁架截面流场模拟分析

3.1 CFD数值计算参数

由于桁架梁的部分构件沿桥梁展向不连续,如牛腿、加强筋等构件,故在计算中不作考虑。本文的CFD 计算模型与试验模型具有相同的比例,即1∶58.6,为准确模拟桁架梁的气动特性,保证了所有通长杆件气动外形相同,CFD计算断面如图6所示。

图6 主梁简化模型

考虑到计算模型沿顺风向的阻塞率应小于5%,同时为了减小流域上、下对称边界对计算断面附近的流动干扰,将计算区域总尺寸设置为17B×50B(B为主梁宽度),最终阻塞率为2.0%。网格系统采用非结构化网格,底层网厚度根据y+控制,在保证其小于1的基础上,第一层网格高度为1.4×10-5D(D为主梁高度)。迎风入口设置为速度入口,流向速度U∞=10 m/s,竖向速度v=0,出口为压力出口,湍流强度设为0.5%,湍流黏性比为10,主梁截面设置为无滑移壁面,计算域设置详情如图7所示。网格系统的整体和局部视图,如图8、9所示。

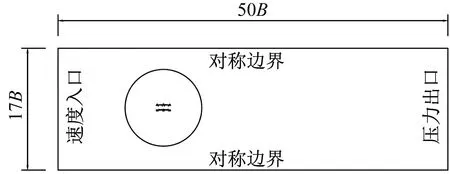
图7 计算域设置

图8 网格整体布置图

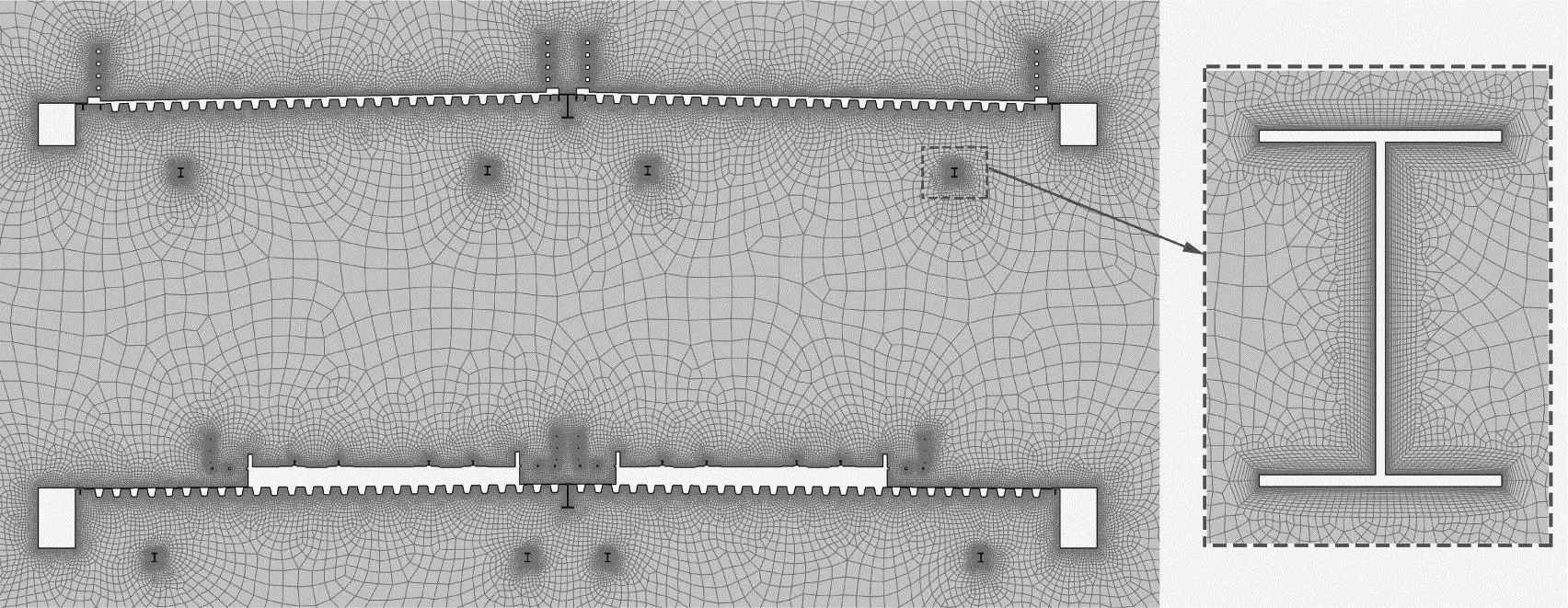
图9 网格局部布置图

本文通过静止绕流方法对网格和时间的无关性进行了验证,如表2所示。综合考虑到计算效率与精度,二维网格总数确定为397 272,采用两方程SSTk-ω模型进行计算,压力-速度耦合算法采用了SIMPLEC算法,数值模拟残差设置为1×10-5,计算时间步确定为0.000 1 s。

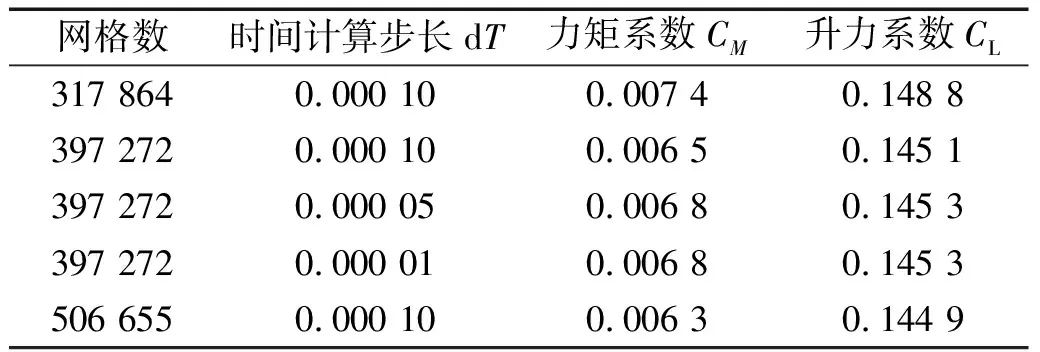
表2 网格无关性验证

3.2 平均流场形态分析

本文通过时均化处理,在涡激振动最大振幅所对应的风速下,对每个工况进行非定常求解至断面出现稳定的旋涡脱落,即升力的时程曲线呈现规律的周期变化,然后对每个工况取至少15个旋涡脱落周期的流场数据进行积分,平均得到时均化的流场数据。其中,0°风攻角下的入口流向折减风速为5.1,-3°风攻角下的入口流向折减风速为4.4。

图10和图11为该桁架断面0°攻角的时均流线图与单个周期内四个时刻的瞬时Q准则。当流动经过断面迎风侧前缘时在上、下转角位置发生气流分离,并且再次附着到断面表面,之后在尾端分离出较高能量的旋涡;上桥面上侧由于栏杆的影响出现了较大尺度的旋涡,尾端存在汇流现象,旋涡交替脱落,产生周期性压力差;下桥面尾端对称脱落出尺度较小的旋涡,其下侧因流动分离产生了高能量的狭长旋涡,且尺度是所有旋涡中最大的,所以可能是导致涡振的主导旋涡。

图10 0°风攻角下时均流线图

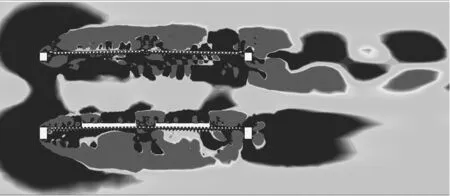
(a) 0时刻

图12和图13为该桁架断面-3°攻角的时均流线图与单个周期内四个时刻的瞬时Q准则。相比于0°攻角下的流场,-3°攻角上桥面上方旋涡尺度显著减小且流动分离减弱,但由于检修车轨道使得下侧的流动分离变得更加剧烈,导致尾流交替脱落的旋涡尺度也相应增大;下桥面尾端分离出的旋涡和其下侧高能量旋涡的尺度进一步增大,并且下侧的主导旋涡还形成了两个明显的涡核。

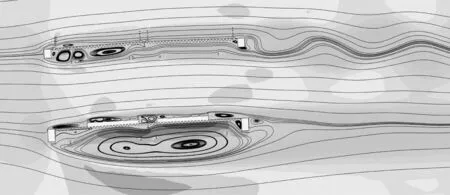
图12 -3°风攻角下时均流线图

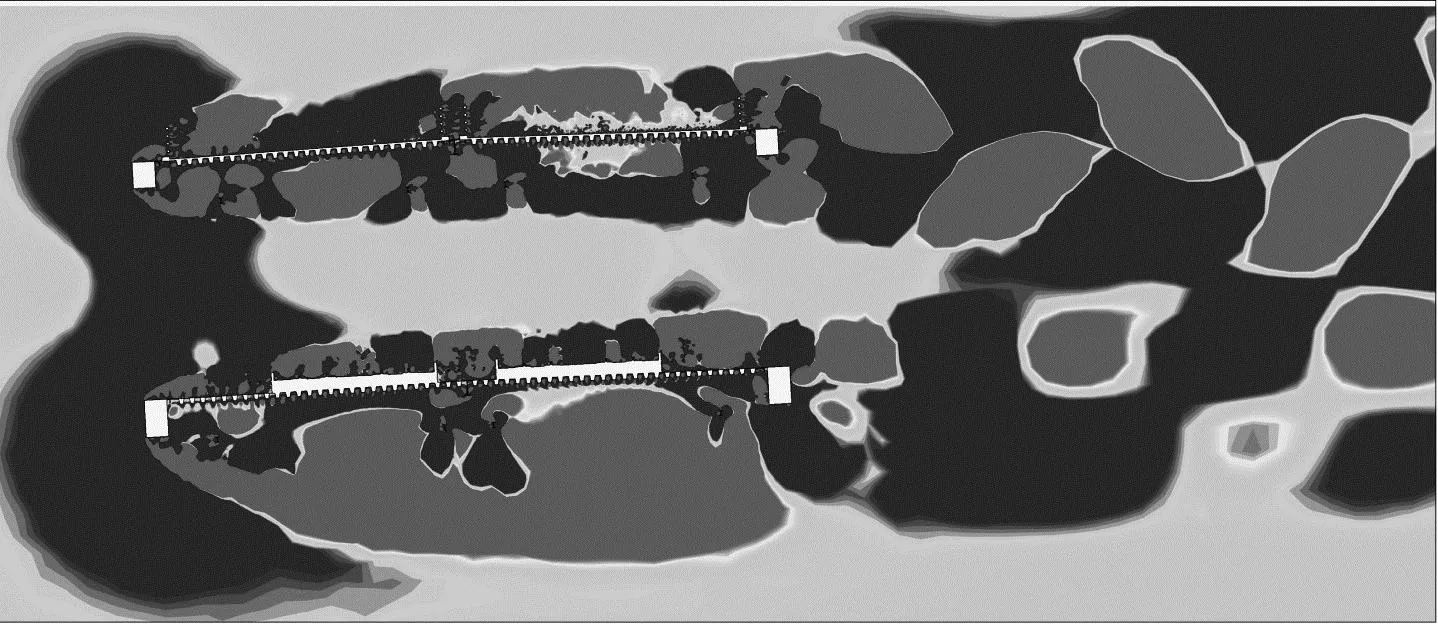
(a) 0时刻

综上所述,导致该断面在0°与-3°风攻角下发生涡激振动的主要原因是流动经过下弦杆分离出的大尺度高能量旋涡,下文将据此进行涡激振动的控制。

4 涡激振动抑制措施

4.1 二维被动控制方法

本文依据数值模拟结果与相关文献[18-20],在风洞试验中设置了不同长度的水平翼板,下中央稳定板和L型分流板来控制主梁的涡激振动,措施详情如表3所示。

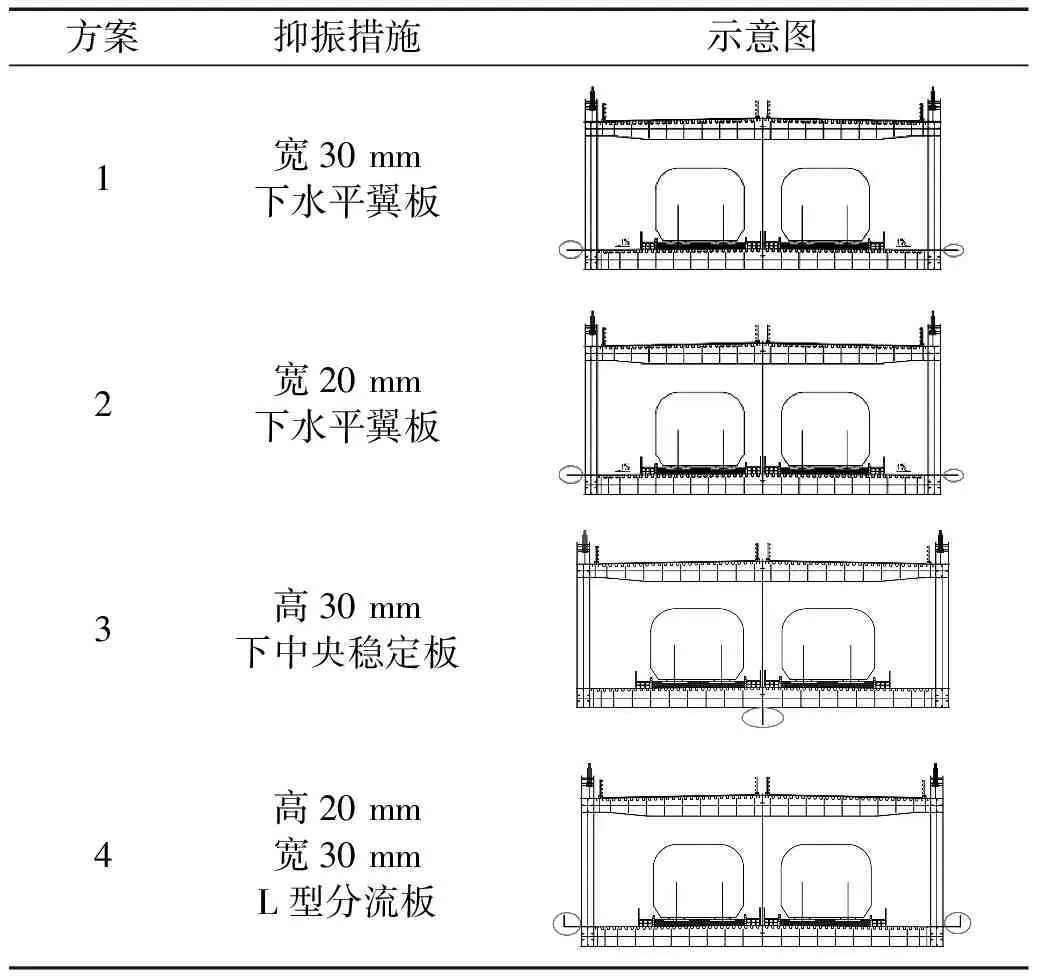
表3 二维被动抑振措施

方案1～4在-3°风攻角下的测试结果,如图14所示。在已测试的方案中,在下弦杆上部设置水平翼板可以抑制部分主梁涡振,方案1的振幅为无措施工况振幅的67%,方案2的振幅为无措施工况振幅的77%;与无措施工况相比,方案1与方案2的涡振起振风速都提高了。在下层桥面下部加中央稳定板对主梁涡振起到了负作用,涡振振幅比其原断面略大,且出现了两个涡振区间。方案4对主梁涡振的抑制效果最好,完全抑制了主梁的竖向涡振,该措施进一步也在α=0°、+3°上进行了验证,结果如图15所示,在三个攻角下都完全抑制了主梁涡振。

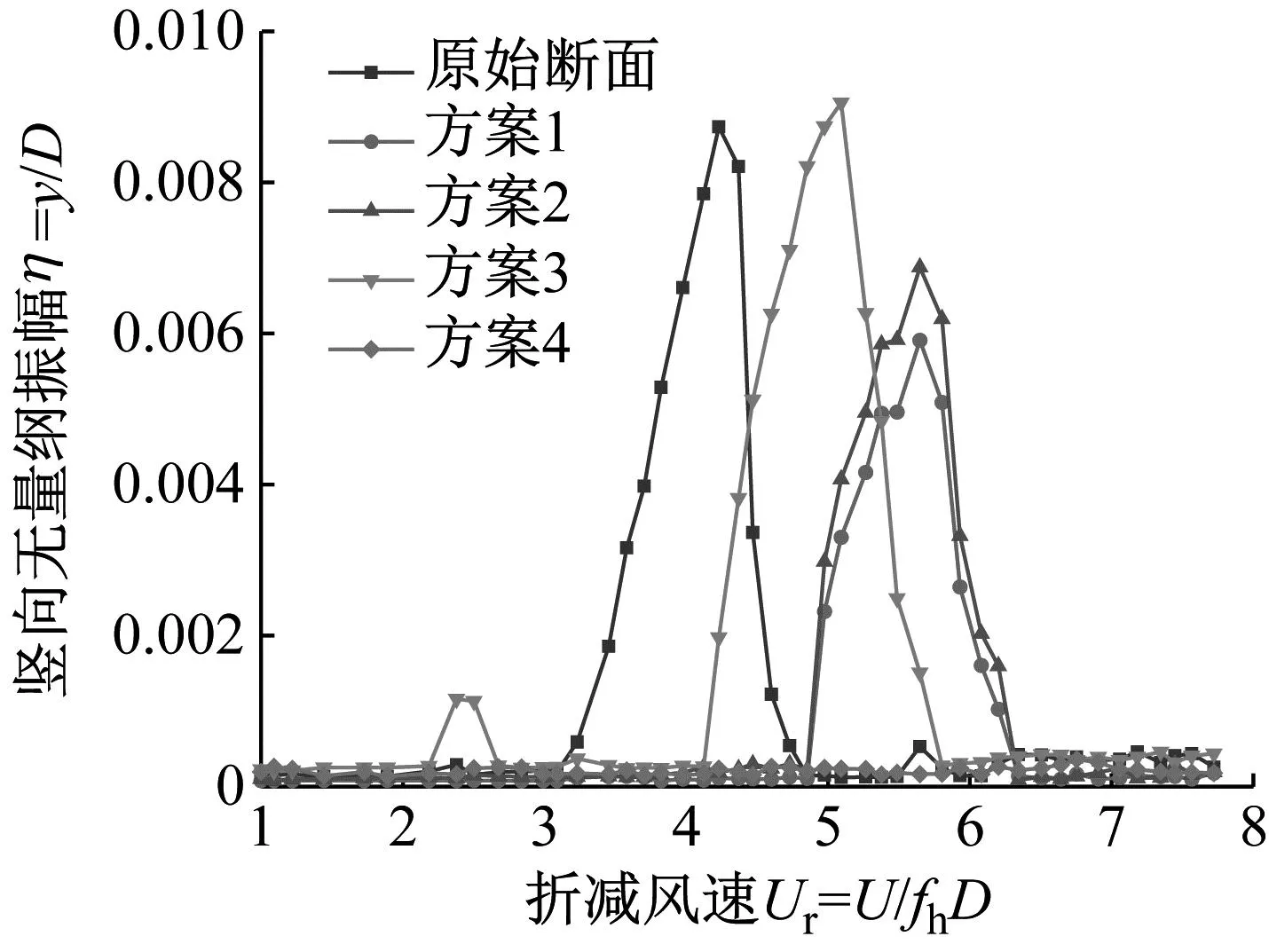
图14 -3°风攻角下各种方案抑振效果比较

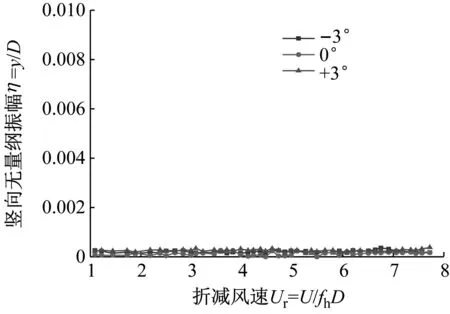
图15 L型分流板措施涡振试验结果

4.2 三维被动控制方法

展向周期摄动方法(spanwise periodic perturbation method) 是一种有效的三维被动控制方法,它将周期性的几何变形用于物体的前缘或后缘,在展向波纹的前缘产生了沿流向与垂直于流向的涡流分量,涡量的重新分布让相互交错的卡门涡街分解为稳定且对称的尾流,从而达到抑制涡激振动的目的[21-22]。展向涡量变化示意图,如图16所示。

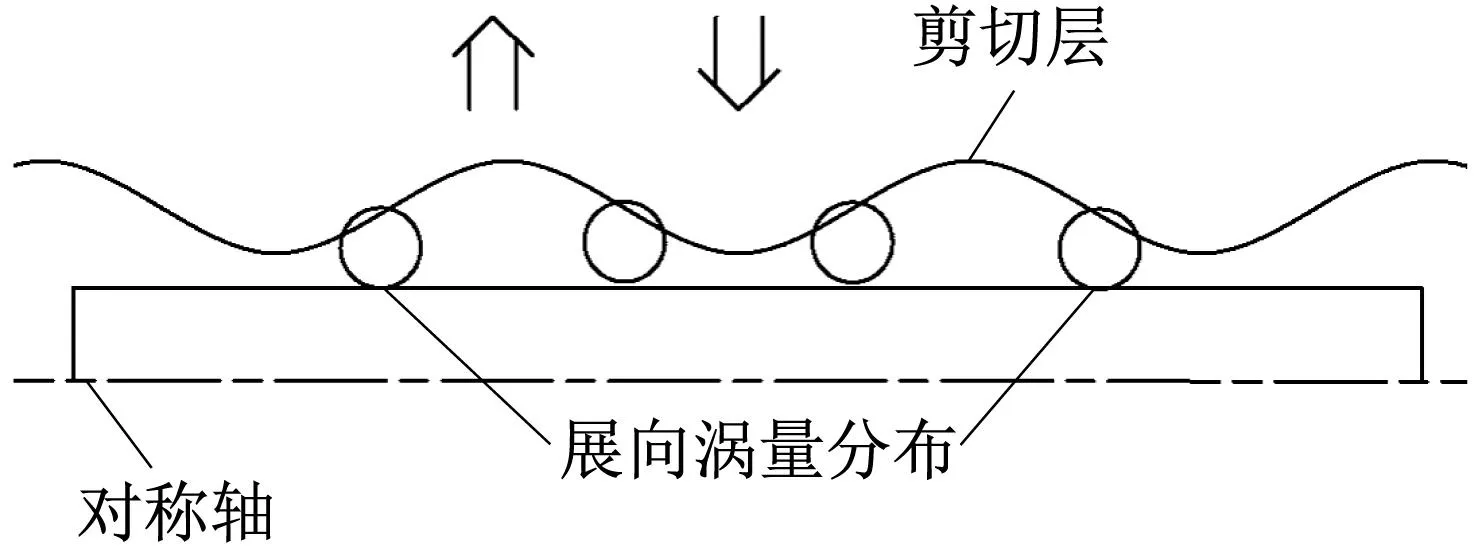
图16 展向涡量变化示意图

使物体表面轮廓沿着展向呈正弦变化是展向周期摄动法的典型应用,Dobre等[23]将方柱的前缘改为波浪形外形,并进行了风洞试验验证了该控制方法对于抑制周期性展向涡脱的有效性。El Gammal等[24]进行了风洞试验以确定展向周期摄动法在控制板梁桥模型的涡激振动方面的有效性,在试验中,截面前缘和后缘的形状被修改为正弦波形,为尾流提供了三维扰动。由于桁架上、下弦杆的构造与板梁截面有相似之处,所以本文受到展向周期摄动法的启发,将展向正弦几何构造做成风嘴,以此对流场施加三维几何扰动并控制该桁架截面的涡振。参考二维控制措施中的方案,只将波浪形风嘴置于下弦杆外侧,对称布置的风嘴可以解决来流风向不确定的问题[25],具体布置如图17所示。

图17 波浪形风嘴措施

基于展向周期摄动法,正弦波形的关键几何参数包括波长W与幅值A[26],如图18所示。然而,尚且不清楚波长和幅值等相关参数应如何确定,所以本文在保证合理性的情况下设计了四种不同几何参数的波形,以此来研究不同几何参数对抑振效果的影响,具体工况设置如表4所示。

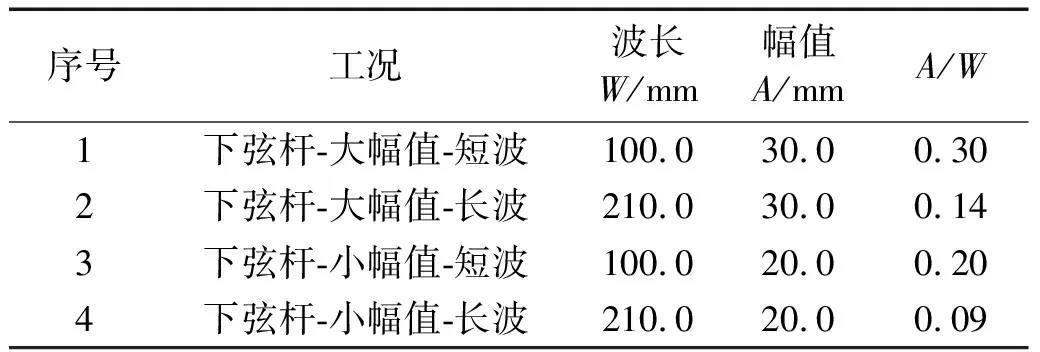
表4 不同几何参数的波形风嘴

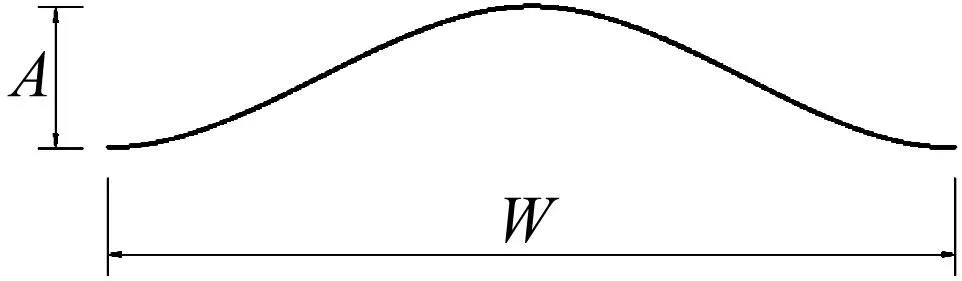
图18 波浪形风嘴几何参数示意图

4.3 波浪形风嘴风洞试验结果与分析

本试验沿用2.1节模型,其他条件不变,波浪形风嘴使用的材料为ABS塑料板,由激光切割后拼接制成,其质量相对于模型整体质量来说可以忽略不计。试验在最不利攻角-3°下进行,得到的无量纲竖向振幅与折减风速的关系如图19所示。

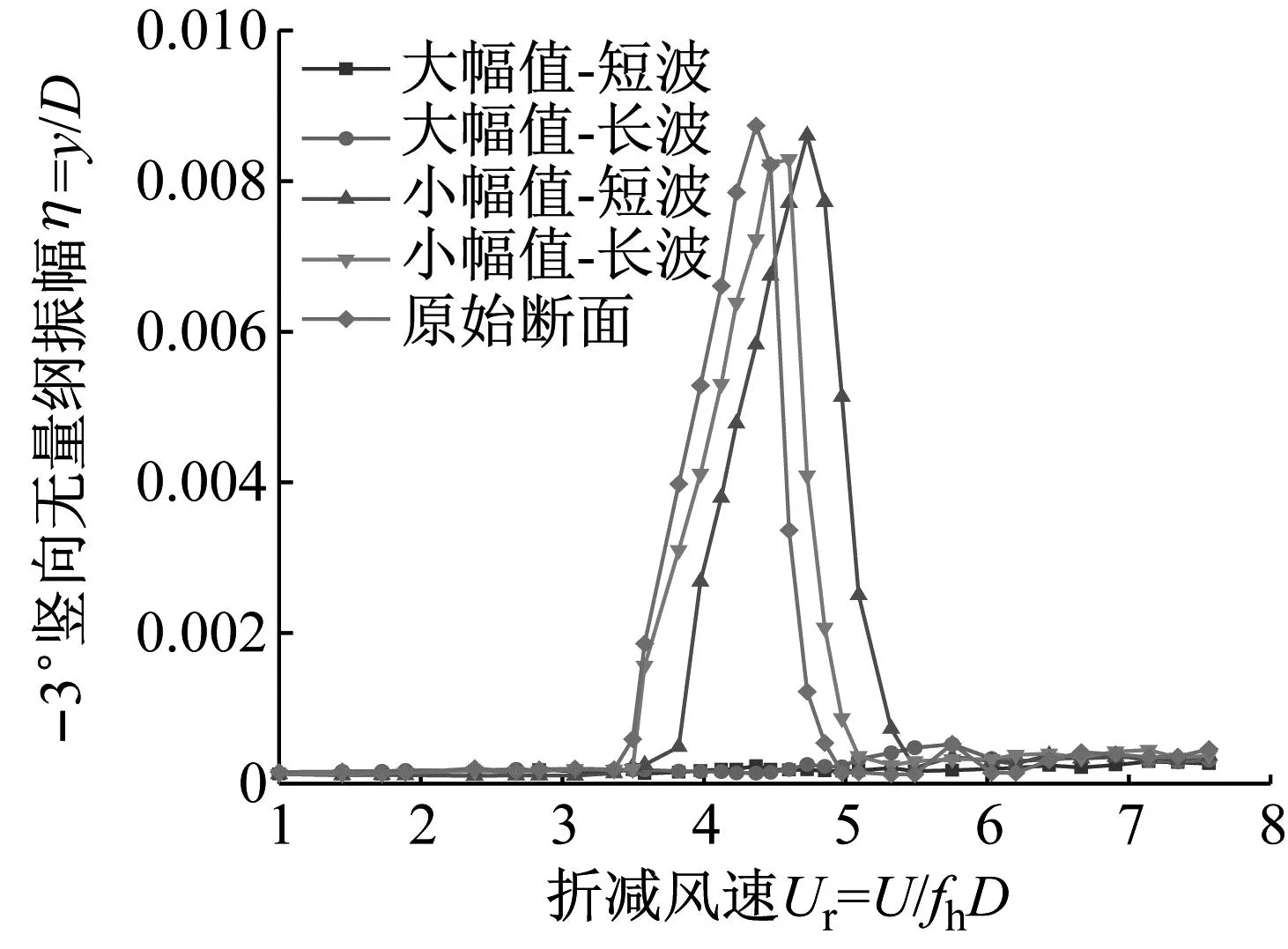
图19 -3°风攻角下不同波浪形风嘴抑振效果比较

试验结果表明:使用大幅值的波浪形风嘴对桁架梁涡振的抑制效果最好,涡振基本消失,小幅值的波浪形风嘴并没有明显改善主梁的涡振性能,两种工况的最大竖向无量纲振幅都与原始断面的最大竖向无量纲振幅接近,且两种工况的涡振区间都略大于原始断面的涡振区间,小幅值-短波风嘴的主要涡振区间位于3.8～5.3的折减风速范围内,小幅值-长波风嘴的主要涡振区间位于3.6～4.9的折减风速范围内。

不同波长、不同幅值的波浪形风嘴抑振效果比较,如图20和21所示。由图20和21可知:随着波浪形风嘴的幅值增大,涡振的振幅减小甚至消失,说明波浪形风嘴的抑振效果对幅值A的变化比较敏感,通过增加幅值A可以显著提高主梁涡振性能;而波长W的改变对抑制桁架梁涡振的效果不是很明显,所以与波长W相比,幅值A对波浪形风嘴的涡振控制效果影响更大。

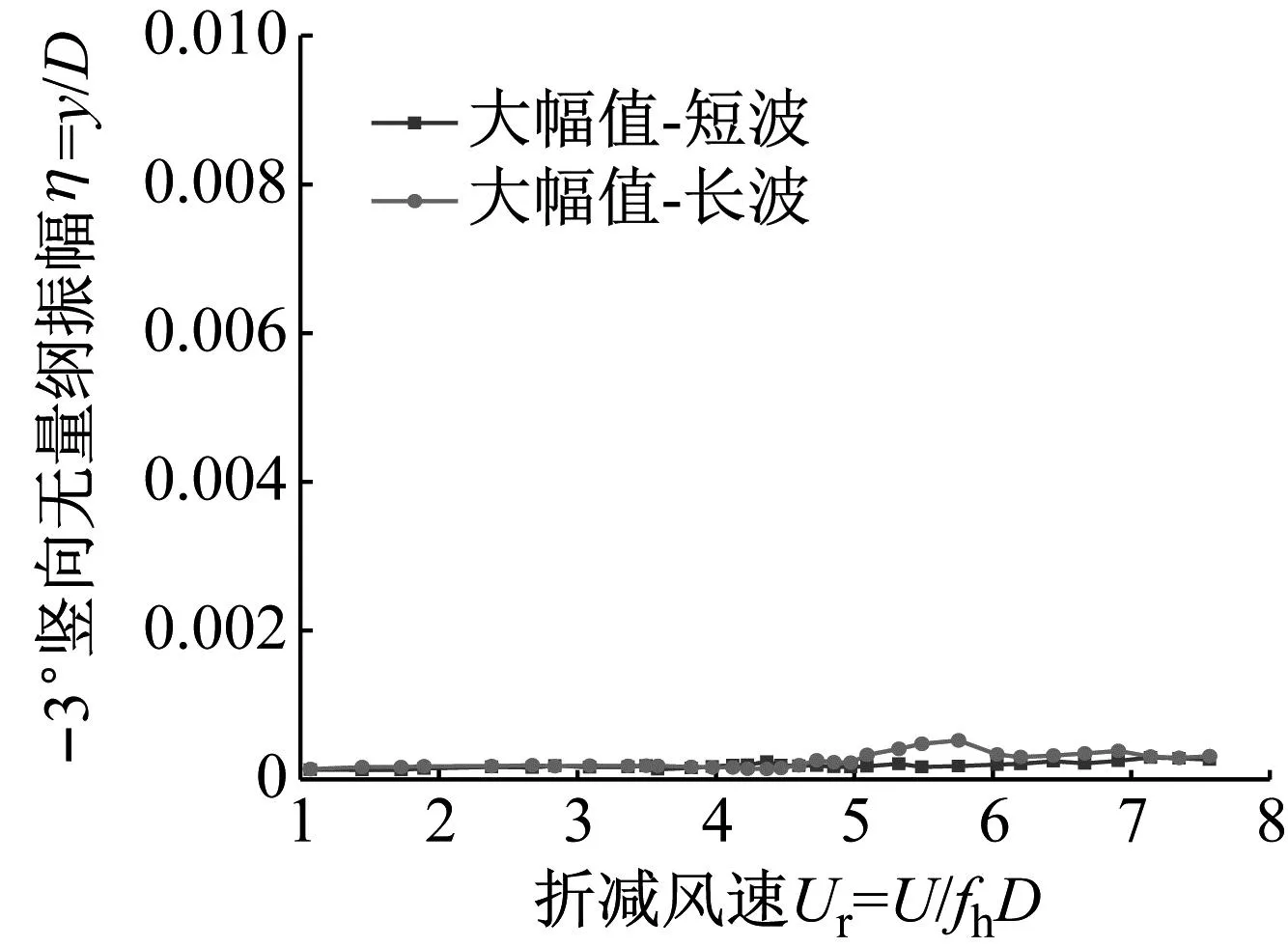
(a) 大幅值波浪形风嘴

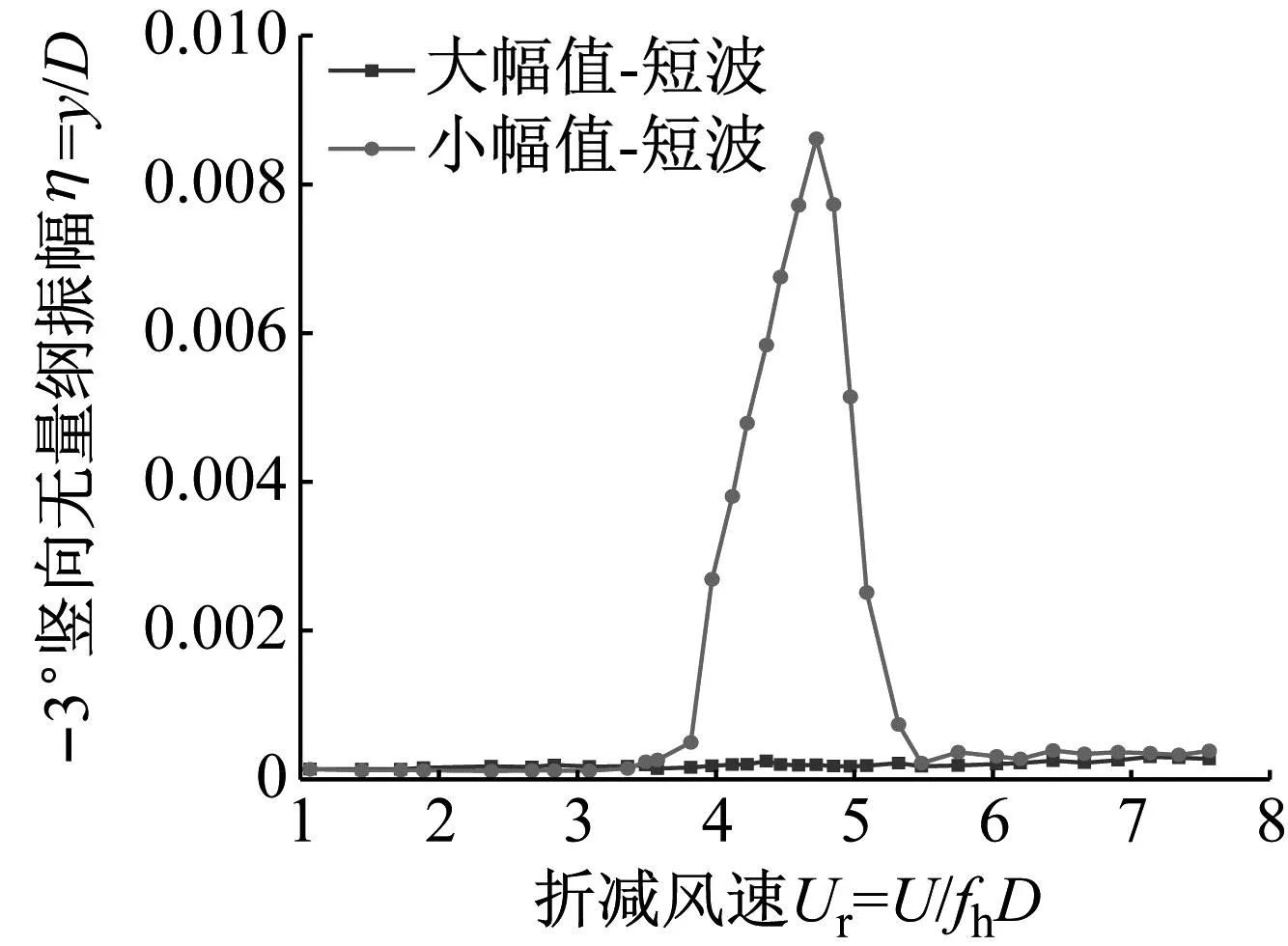
(a) 短波波浪形风嘴

5 结 论

本文针对大跨度公铁两用双层桁架桥进行了风洞试验,研究了其涡激振动现象,并提出了相应的二维与三维气动控制措施,将展向周期摄动法应用于该桥上,控制了主梁的涡激振动,主要研究内容总结如下:

(1) 当模态阻尼比为0.42%时,在0°与-3°风攻角下,主梁原始断面发生明显的竖向涡激振动。0°攻角下主要涡振区间位于3.7～4.6的折减风速范围内,最大竖向无量纲振幅为8.7;-3°攻角下涡振振幅相对较大,主要涡振区间处于4.4～5.5的折减风速范围内,竖向无量纲振幅为8.8。在0～25 m/s的常遇风速区间内,各攻角均未发生明显的扭转涡激振动。

(2) 在0°与-3°风攻角下,钢桁主梁下弦杆的下转角处因流动分离产生的高能量大尺度旋涡是影响断面流场的主导旋涡,也是诱发竖向涡振的主要原因。

(3) 采用不同尺寸的下水平翼板,下中央稳定板以及L型分流板对主梁的涡激振动进行控制。30 mm宽的下水平翼板使竖向振幅减小33%,20 mm宽的下水平翼板使竖向振幅减小23%,下中央稳定板使主梁竖向涡激振动振幅增大,而L型分流板在三个风攻角下完全抑制了主梁涡激振动。

(4) 基于展向周期摄动法设计了不同波长与幅值的波浪形风嘴,并进行了风洞试验,结果表明波浪形风嘴的抑振效果对幅值变化比较敏感,增大幅值可以有效抑制主梁的涡激振动。

(5) 本文的三维展向气动控制措施还需进一步优化,后续试验将在大比例尺模型上进一步检验不同缩尺比下的控制效果,并通过数值模拟来研究其抑振机理。