基于动作捕捉与深度学习的跳跃荷载重构方法
王浩祺,于秉仟,陈 隽
(同济大学 土木工程学院,上海 200092)
伴随着我国城镇化国家战略的持续推进,大量人口正在或即将涌入城市。城镇居民对城市基础设施不断提高的功能需求推动了大型公共建筑向更长、更轻、更柔的趋势发展。由于这类结构通常采取较为轻盈的结构设计,具有阻尼小、基频低的特点,在承受人致动力荷载时更容易产生振动,导致“振动舒适度”问题[1]。在典型的人致荷载类型中,跳跃对结构产生的冲击作用最大,引起的后果通常也更为严重[2]。例如,瑞典某体育馆在观众进行有节奏的跳跃作用下产生了严重的基础破坏[3]。韩国一座高层建筑因17个成年人的节奏性健身产生了大幅振动,造成1 500亿韩元的经济损失[4]。2018年,我国南京某体育馆楼板由于观众的集体跳动产生了剧烈振动,致使演唱会开始20 min后即提前终止,引起舆论的广泛关注。这些典型事例表明,跳跃荷载引起的人致振动问题会造成严重的经济损失和恶劣的社会影响。
目前针对跳跃荷载的研究工作主要依赖于人致荷载动力测试。在研究的最初阶段,研究者首先采用测力板方法对人致荷载进行测量[5],随后又引入了广泛应用于体育运动学的测力鞋垫技术[6-7],突破了测力板在空间上的尺寸限制。随着研究的不断进展,人们认识到单人运动对结构的影响通常十分有限,结构的振动舒适度问题常由多人协同运动产生,而受设备或场地条件所限,以测力板为代表的单人荷载测试方法难以应用于广泛的人群荷载试验[8]。另一方面,以视觉技术为代表的间接测量技术提供了一种新的思路。Fujino等[9]通过分析一次约有2 000名行人涌上桥面的录像发现人步行时中心轨迹呈“之”字型,这是文献中可见的在土木工程领域最早采用视频方式进行人体运动分析的报道。Caprioli等[10]利用摄像机拍摄人体运动视频,并基于粒子图像测速法(particle image velocimetry,PIV)分析视频,成功提取了人体运动轨迹。Mazzoleni等[11]采用数字图像关联法(digital image correlation,DIC)获得了人体运动时身体各部位的加速度。Celik等[12]用光流法捕捉到人体运动轨迹。然而,上述方法在反算人致荷载时均采用了简单的单刚体人体模型,其重构的动力荷载在高频阶段均不够精确。
深度学习技术是一种通过对大量实测数据的训练来构建物理量之间联系的方法[13],经过训练后的深度神经网络可以有效表达物理量之间复杂的非线性关系。其中,卷积神经网络最早作为一种用于图像识别的方法被提出[14],这种方法可以视为一个沟通了输入与输出之间关系的高维非线性函数,其训练过程则为卷积核及权重优化的过程,适宜用于表达难以解析描述而实际存在关联的映射关系。这为解决人致荷载的机器视觉研究提供了新思路。
与地震动、风、车辆等动力荷载不同,人致荷载涉及“人”的参与,因此,研究必然涉及土木工程与医学和运动生物力学等领域的交叉。由于人致荷载是人体运动的结果,因此,研究人致荷载需要从人体运动着手。据此,基于医学领域的三维动作捕捉系统试验,同步实测人体单次跳跃的运动轨迹和地反力曲线,在9 985条记录基础上,研究单次跳跃地反力曲线的控制参数,进一步建立人体运动轨迹与跳跃荷载关键参数的卷积神经网络模型,最终将人体特征点轨迹转换为地反力。
1 跳跃荷载测试
1.1 试验介绍
大量的实测数据是进行深度神经网络训练与预测的基础。为此,开展了跳跃荷载动力特性试验以获得配对的轨迹与地反力数据。试验共招募了27名志愿者进行了跳跃测试,测试者的基本信息如表1所示。每位测试者按照1.50 Hz、2.00 Hz、2.67 Hz、3.50 Hz等四个固定频率和一次自选频率各完成一次30 s左右的跳跃。在跳跃过程中,利用采样频率为1 000 Hz的AMTI OR6-7型号高精度测力板记录跳跃引起的地反力,在人体上39个特征部位粘贴了反光标记物(具体位置见表2),其轨迹可由设立在周围的红外摄像机捕捉。该相机的采样频率为200 Hz,空间定位精度为0.1 mm。摄像头、测力板位置及实验室整体环境,如图1所示。
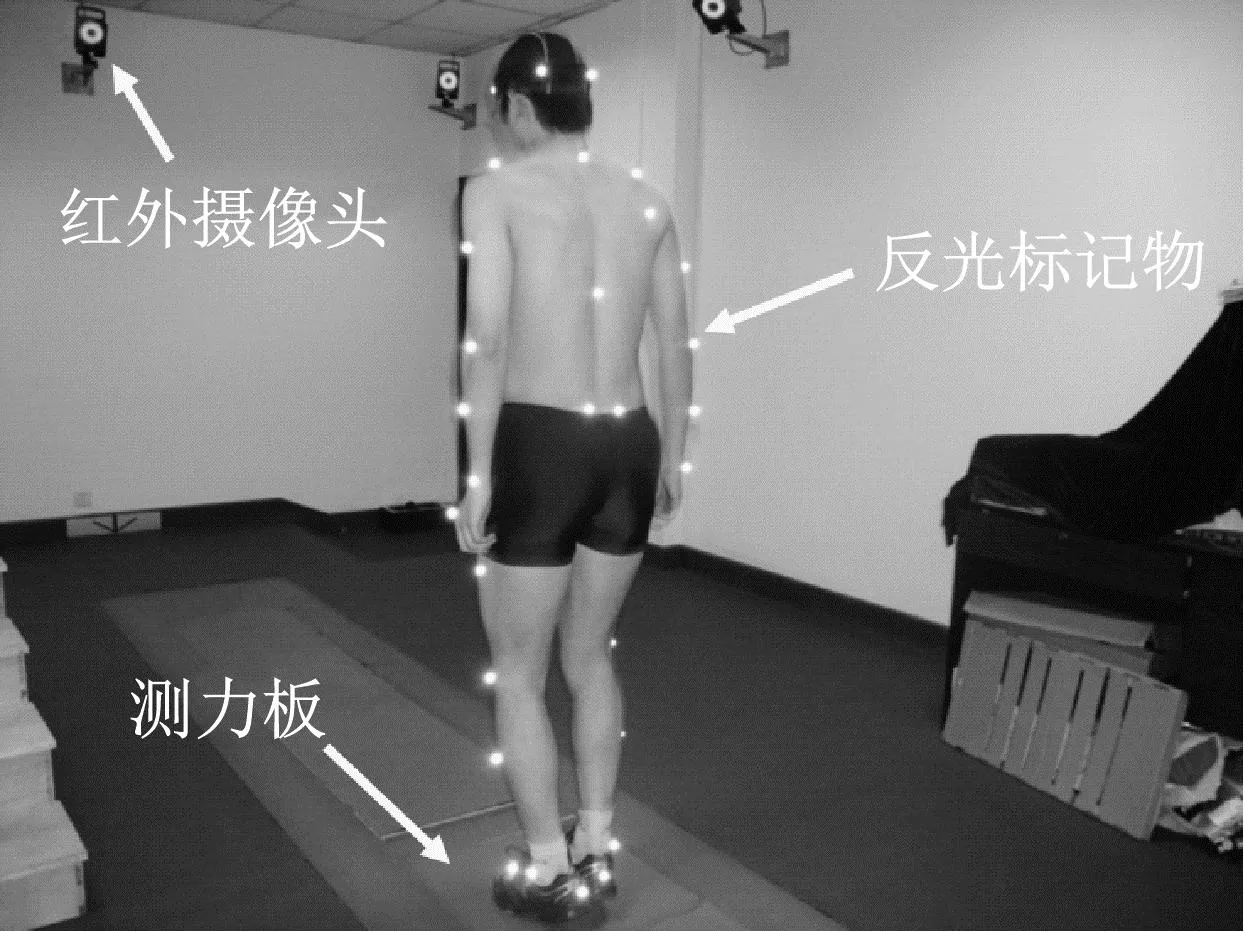
图1 试验场景示意图

表1 测试者年龄、身高、体重均值统计[15]

表2 反光标记物位置
1.2 典型数据分析
某测试者按照1.50 Hz的频率进行跳跃时测力板记录的地反力时程曲线及其对应的频谱,如图2所示。由图2可知,跳跃荷载存在多个卓越频率,分别为跳跃频率及其倍频。对于承受跳跃荷载的工程结构,当其基频与任意一个卓越频率接近时,均可能引发结构的类共振效应,产生振动舒适度问题。因此,合理的荷载重构方法应当能够保证重构后的荷载各阶频率上的峰值均能够与真实荷载的对应峰值接近。
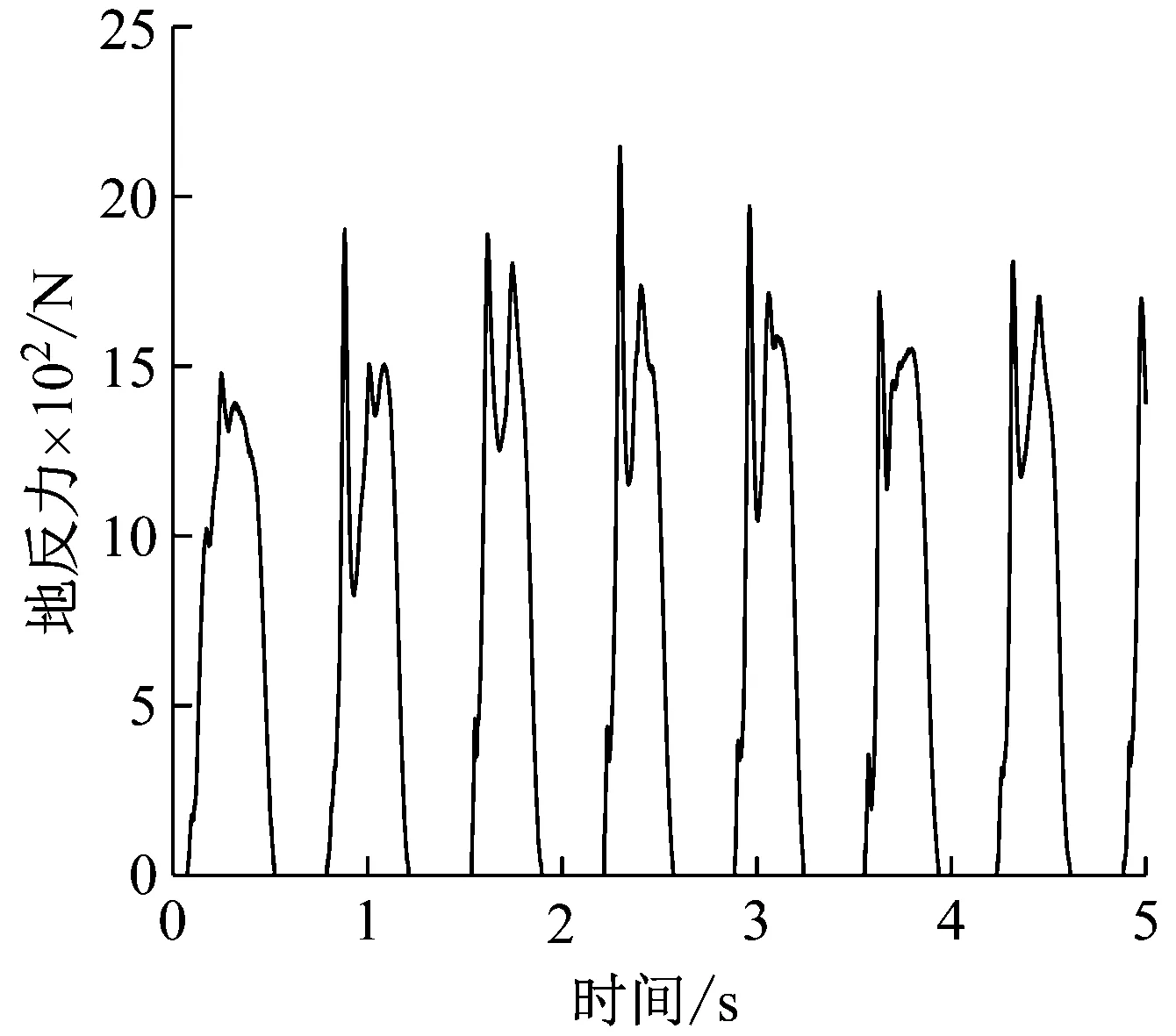
(a) 时程曲线
图3展示了躯干处(位于胸腔正面)和下肢膝盖处的两个反光标记物的轨迹(图3(a))以及经过两次求导后的加速度时程曲线(图3(b))及其傅里叶幅值谱(图3(c))。两个位置特征点轨迹的位移曲线区别不大,但经两次求导之后,加速度时程的区别十分明显。位于下肢的反光标记物加速度曲线含有明显高频成分。进一步采用式(1)分别计算头部、躯干、上肢、盆骨、下肢等代表点处反光标记物轨迹位移与轨迹加速度与躯干处对应物理量之间的相关系数
(1)
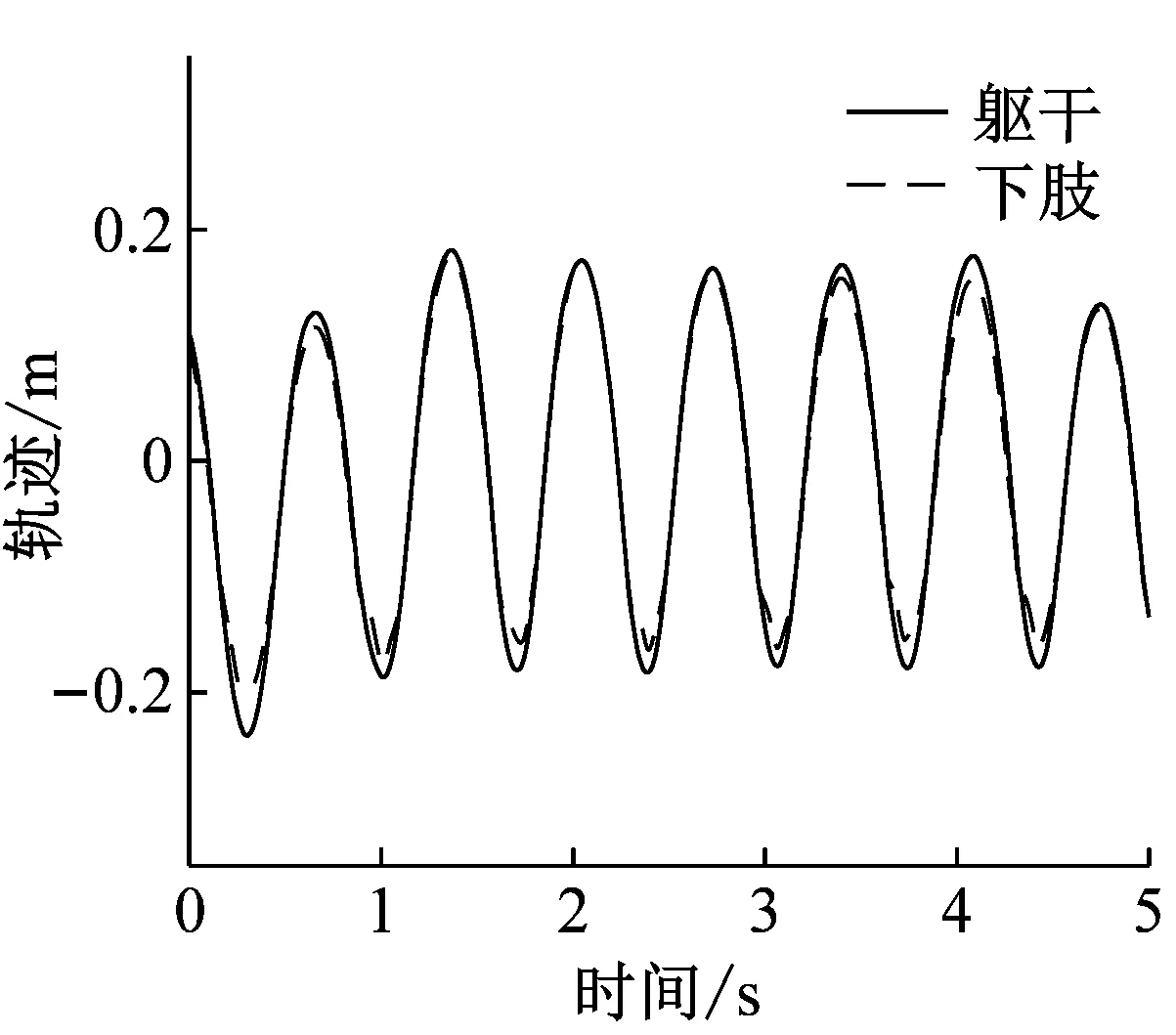
(a) 轨迹时程
式中:xi、yi分别代表该物理量各个元素的取值;上标“-”表示平均值。相关系数结果如图4所示。由图4可知,各个主要特征点的轨迹位移相关系数接近于1,表明其具有较强的相关性,但从轨迹加速度来看,越接近下肢的特征点其相关系数逐渐降低,其原因在于人体跳跃时下肢存在屈膝—直立的过程,与躯干相比增加了显著的高频分量(图3(b))。因此,仅采用上身轨迹并基于单刚体模型和牛顿第二定律进行地反力预测的方法存在因忽略跳跃荷载高频成分而导致的误差[16]。

图4 人体各位置运动轨迹与躯干处轨迹相关系数
2 跳跃荷载模型
2.1 跳跃荷载曲线的三参数模型
观察图2(a)的跳跃荷载时程曲线,发现连续的跳跃荷载可看作多个单次跳跃的组合。从测试者自腾空状态落地这一刻起,至测试者再次进入腾空状态为止,测试者与地面存在接触,对地面产生作用力,在时程曲线上表现为一脉冲段。在腾空状态,测试者与地面不产生接触,因此测力板数据呈现一个零平台段。一个脉冲段与一个零平台段共同构成了一个完整的跳跃周期。
图5是一个完整的跳跃周期示意图。图5中:Fmax为本跳跃周期内的地反力最大值;TP为两次落地之间的时长;tP为脉冲段时长。将以上参数进行归一化,可得到单次跳跃荷载的特征参数,见式(2)
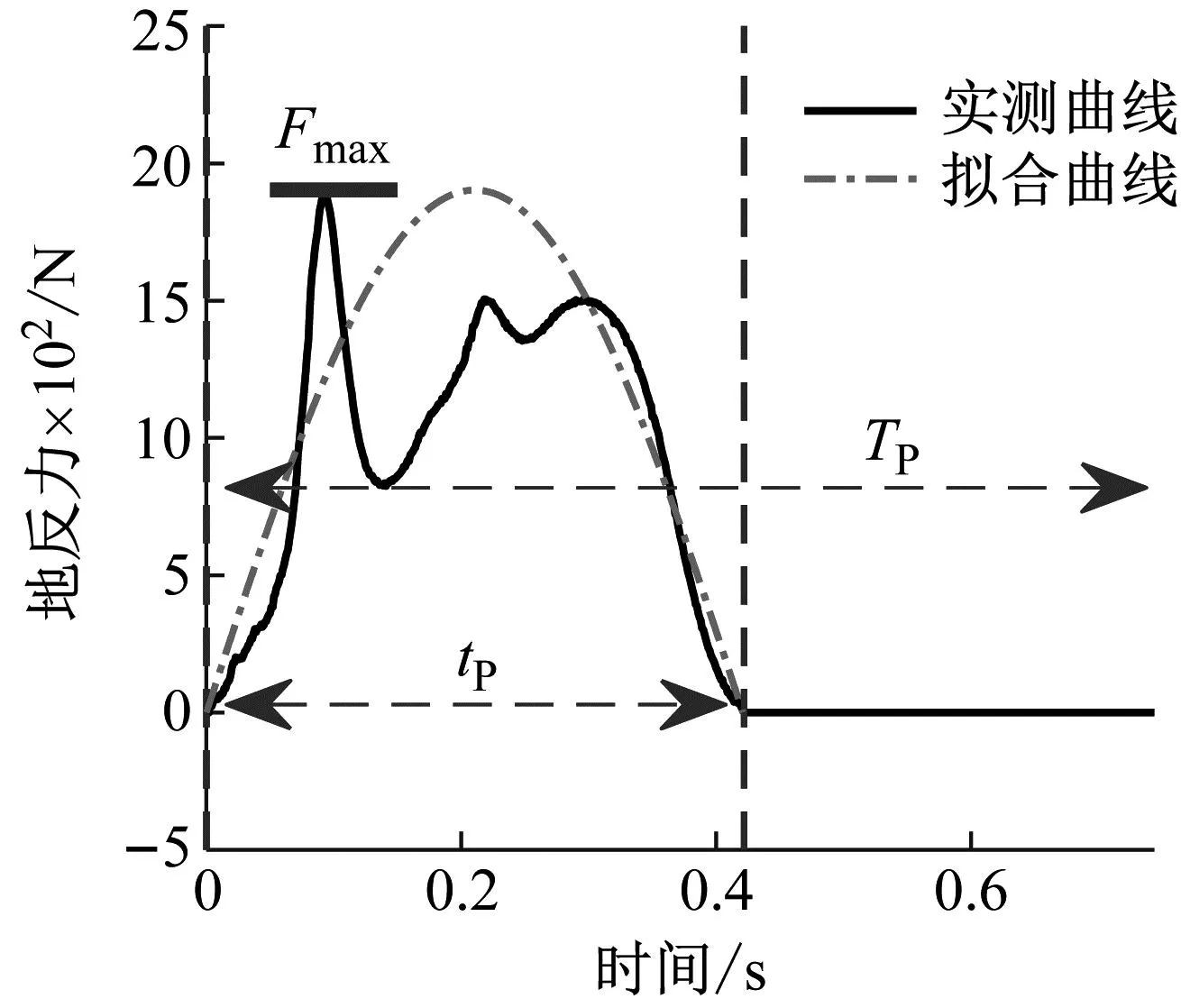
图5 单次跳跃特征参数示意图
KP=Fmax/G,fP=1/TP,α=tP/TP
(2)
式中,KP为脉冲系数,定义为地反力最大值与体重G的比值;fP为跳跃频率;α为接触率[18]。
由实测的跳跃荷载曲线可以看出,通过定义脉冲系数KP、脉冲段时长tP和两次落地之间的时长TP这三个参数,可以描述出单次跳跃曲线的主要特征。因此,研究者曾基于以上三个基本参数,提出了式(3)所示的跳跃荷载模型[17]。将三参数模型应用于拟合单次跳跃曲线的拟合效果仍示于图5。从图5更可以看出,三参数模型在描述跳跃荷载峰值时效果较好,但可能失去时程曲线的细部特征。
(3)
2.2 跳跃荷载曲线的多参数模型
上述三参数模型在一定程度上能够反映跳跃荷载的基本特征(如周期、峰值等),但采用一个半正弦模型模拟单次跳跃会忽略荷载曲线的细部特征(图5)。另一方面,有研究表明,基于标准正交基的荷载分解方法对于动力荷载具有较好的拟合效果[18-19],因此,采用傅里叶标准正交基对荷载脉冲段进行正交分解与拟合。对于跳跃荷载的脉冲段,基于傅里叶正交基的表达式如式(4)所示
(4)
式中:F(t)为跳跃荷载的反力脉冲段;N为傅里叶正交基的阶数;a0、an、bn为各阶傅里叶系数。其表达式由式(5)所示
(5)
研究表明,对于单步人致荷载,采用5-6阶傅里叶级数即可较好地反映单步荷载曲线的特征[20]。采用6阶傅里叶级数模型拟合图5中的单步跳跃荷载曲线的效果,如图6所示。
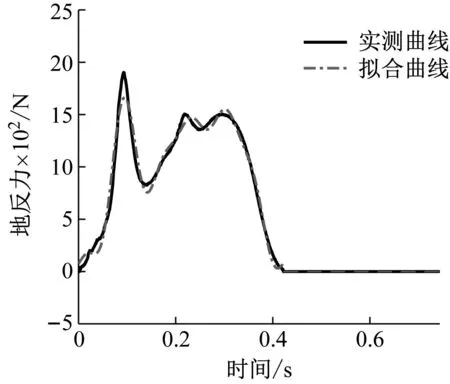
图6 单次跳跃曲线多参数拟合结果(N=6)
3 三参数模型识别与重构
对于单次跳跃荷载的三个基本参数,其中的单次跳跃频率fP、接触率α均可由计算机视觉技术提取人体落地和腾空时刻而直接获得,因此不作为卷积神经网络的输出。本章将利用卷积神经网络训练轨迹与脉冲系数KP之间的关系。采用的网络结构如图7所示。该网络具有两个卷积层和一个全连接层,在每个卷积层后面设置常用的Relu函数以增强网络的非线性学习能力。输入端为一个M行矩阵,当仅采用单个特征点的轨迹作为输入时,M取值为1,此时输入矩阵退化为一个一维行向量。当采用多个特征点的轨迹作为输入时,M为采用的轨迹种类的个数。网络的输出端为包含了X个地反力特征参数的向量,当采用三参数模型时,X取值为1,即对应脉冲系数KP,当采用多参数模型时,X与相应的阶数有关,对于6阶傅里叶级数模型,X取值为13。
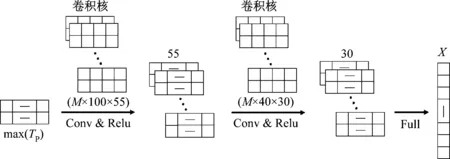
图7 本文采用的卷积神经网络结构
3.1 以躯干处特征点作为输入
第2章所述的跳跃荷载试验获得了总计9 985条单次跳跃轨迹与地反力的配对数据。采用8∶2的比例将这些配对数据分为训练集和测试集,且测试集同时作为训练过程中的验证集。每250次迭代后利用测试集验证训练效果以防止产生过拟合现象。由于验证集的损失函数存在振荡,因此当验证集的损失函数超过之前损失函数的最小值5次时,即认为已经达到了较好的训练效果并终止训练。训练过程中均方根误差和损失函数随训练次数的变化曲线,如图8所示。训练过程采用了随机梯度下降算法。
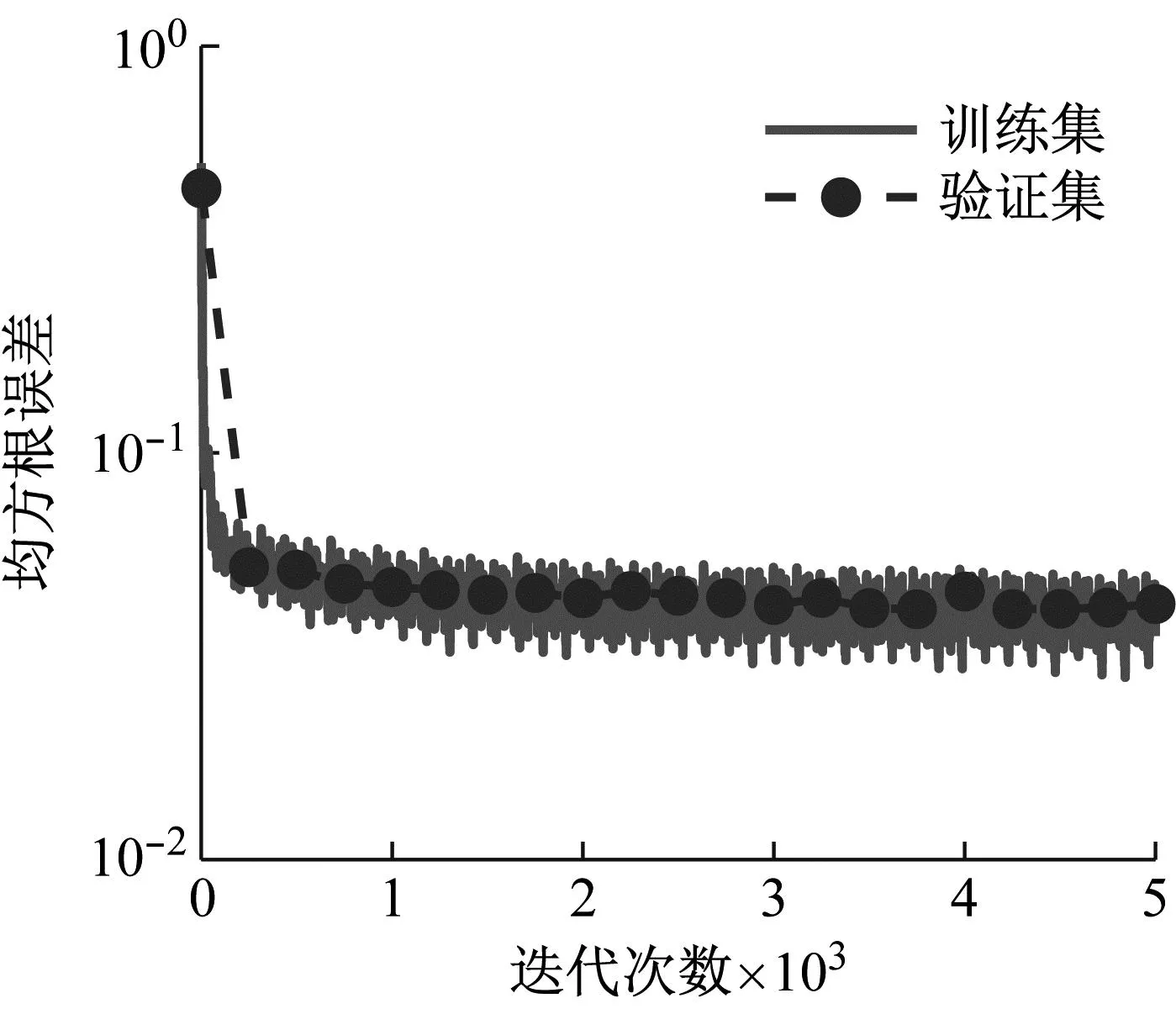
(a) 均方根误差
训练结束后,利用测试集对训练出的网络进行测试,获得的三参数预测结果如图9所示。由图中结果可见,测试集均围绕在y=x直线附近,表明网络已经成功抓取了轨迹与特征参数的联系。在不同的跳跃频率下,预测值与实测值相对误差如表3所示。由于人体在低频跳跃时容易呈现“双峰”的特征(见图5),其时程曲线与高频跳跃时相比更为复杂,因此,表3所示的脉冲系数预测值的平均误差随着跳跃频率的增大呈现降低的趋势。
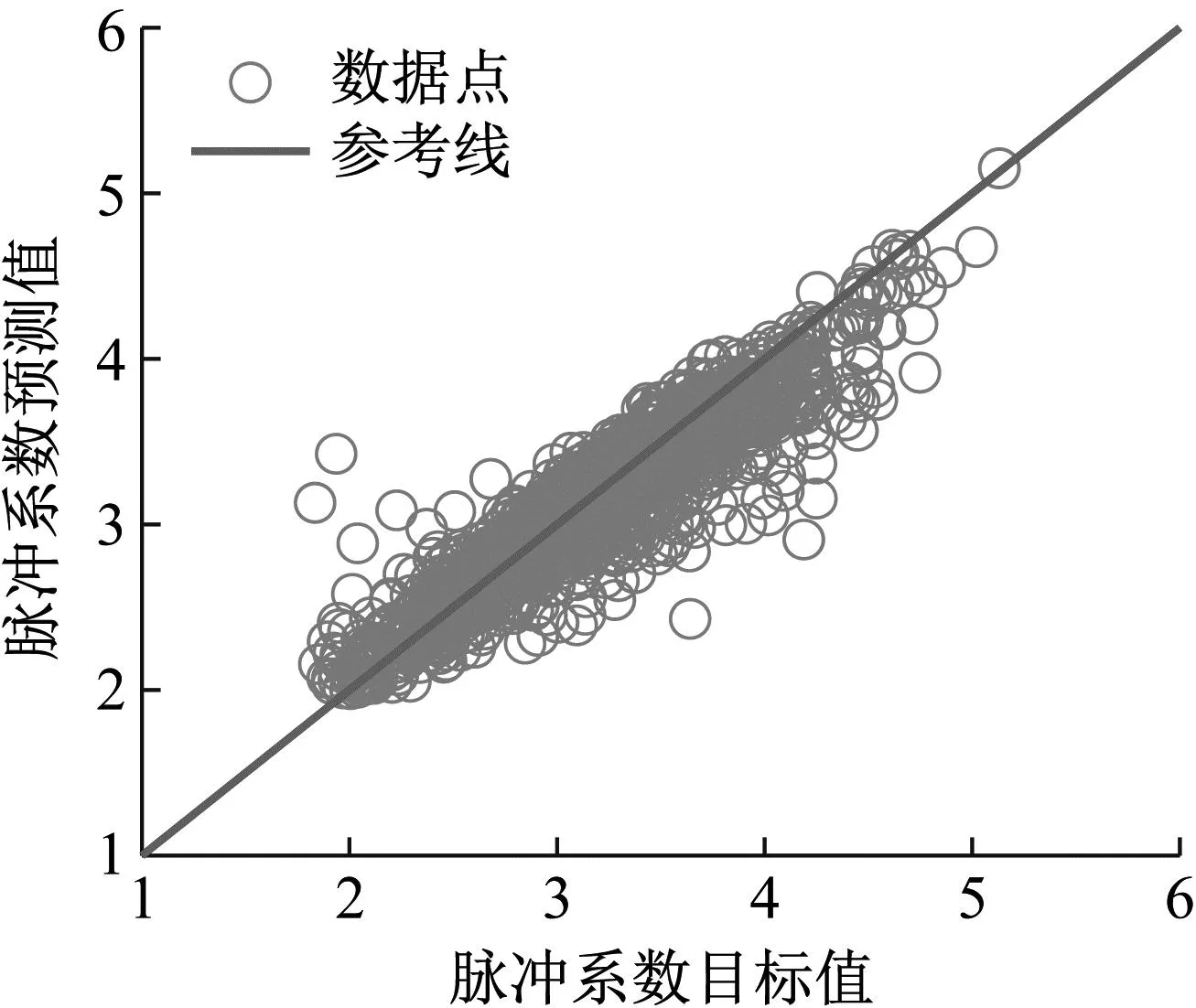
图9 单一输入下三参数模型训练结果

表3 单一输入下目标值与预测值相关系数
为进一步测试训练效果,将训练好的网络用于预测某一测试者连续跳跃的地反力。某一跳跃频率为1.50 Hz的地反力实测时程和预测时程及其对应的傅里叶幅值谱,如图10所示。由图10可知,首阶幅值预测效果较好,但对于高阶分量,预测值的峰值明显低于实测取值,其主要原因为实测时程曲线通常具有多峰特性,而三参数模型仅采用简单的半正弦代表单次跳跃曲线,可能丢失高频信息。
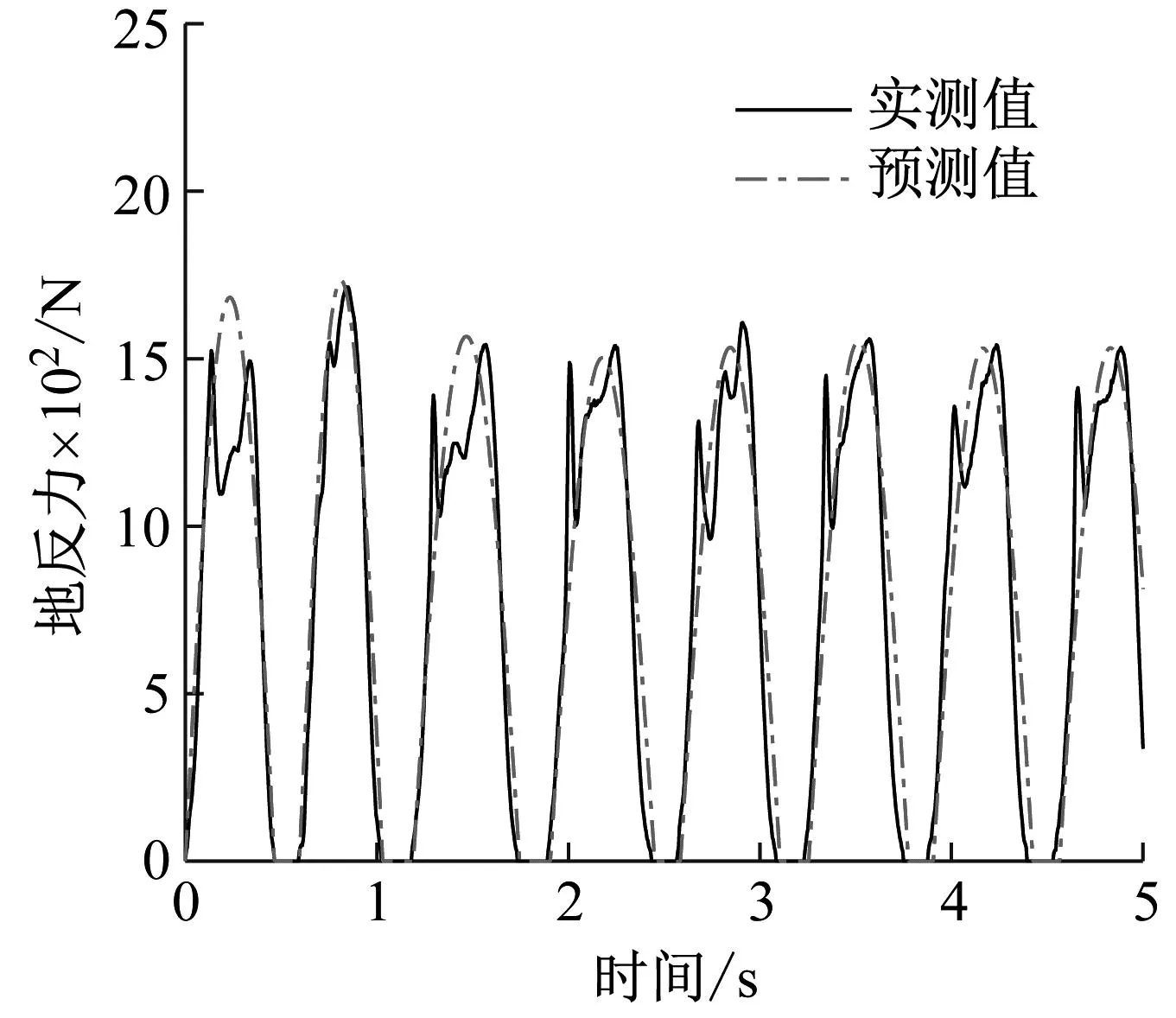
(a) 时程曲线
3.2 以躯干和下肢处轨迹作为输入
在3.1节中,仅采用躯干处的反光标记物作为卷积神经网络的输入,并通过该处轨迹预测脉冲系数的取值。然而,如前所述,躯干位置的轨迹丢失了下肢处的高频信息。为此,本节将躯干处和下肢处的轨迹共同作为卷积神经网络的输入。训练过程及其它网络参数与上一节相同。
本次网络训练的均方根误差与损失函数随迭代次数的变化,如图11所示。与图8对比可见,均方根误差和损失函数均存在一定幅度的降低,表明采用两个输入后,网络的训练效果有所提升。表4所列出的是采用两个输入时目标值和预测值的误差,可以看出对于各个频率范围,其脉冲系数预测值的平均误差较表3所列数值均有所降低。
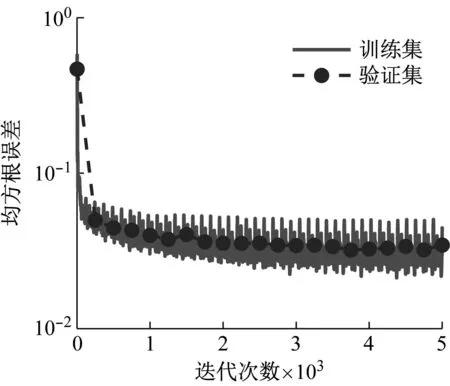
(a) 均方根误差

表4 多输入下目标值与预测值相关系数
4 多参数模型识别与重构
将卷积神经网络方法用于单次跳跃荷载傅里叶级数模型的预测。由于上一节已经证明采用多输入优于单一输入,因此本章网络的输入端仍然采用躯干处与下肢处的运动轨迹。网络输出为各阶傅里叶系数。对于6阶傅里叶级数模型,输出向量共包含13个元素。训练过程如图12所示。从图12看出,由于输出参数较多,网络需要更多的迭代次数才能满足终止训练的要求。参数数量增多同时导致了均方根误差和损失函数的收敛值均高于图8和图10中的训练结果。
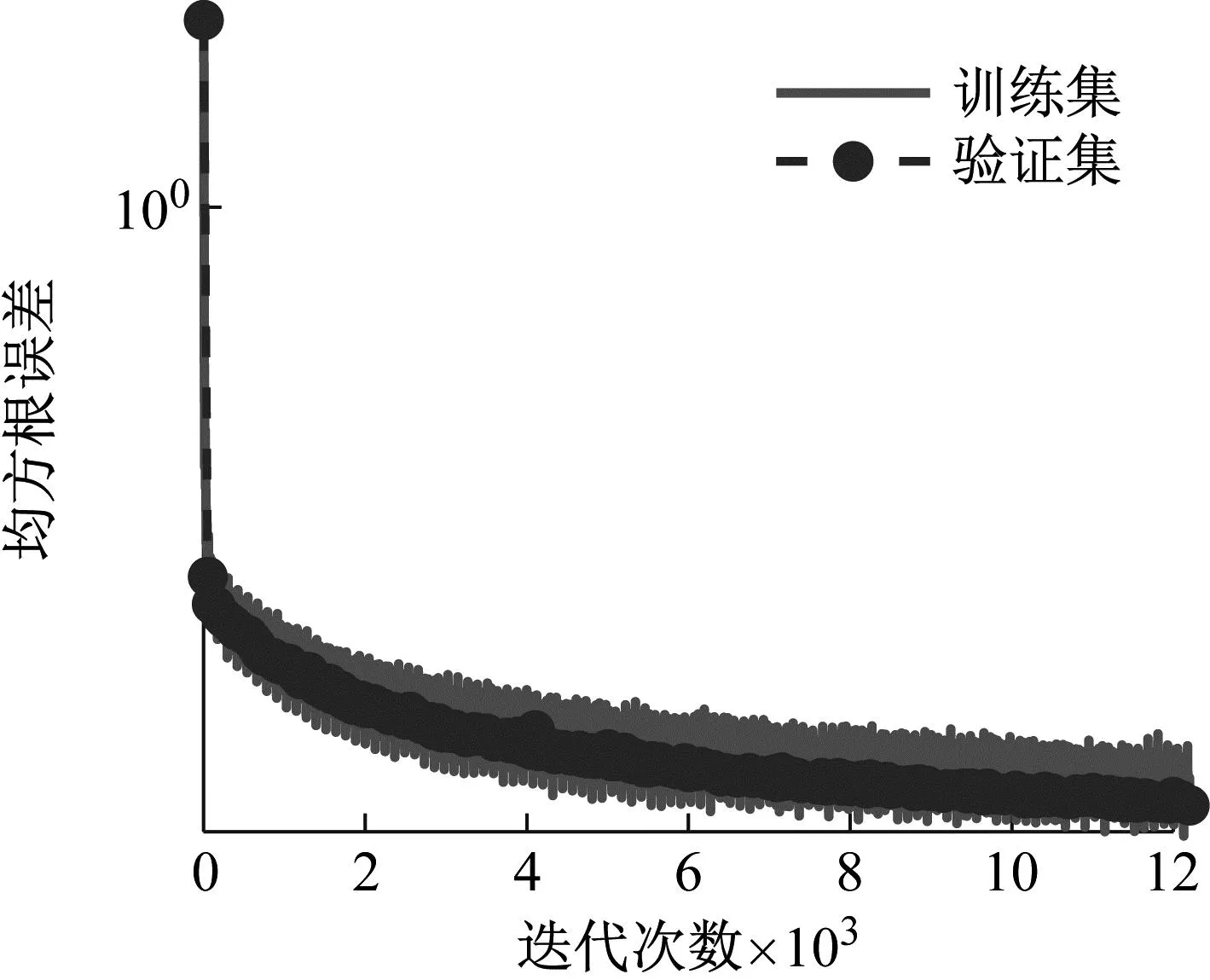
(a) 均方根误差
由于网络输出参数较多,篇幅所限,仅画出a0、a1、b1三个主要参数的目标值与预测值的对比图,如图13所示。由图13可知,各个数据点仍然围绕在y=x直线附近,表示网络已经拾取了轨迹与傅里叶系数之间的联系。同时,根据式(1)的定义计算了总计13个参数预测值与目标值的相关系数,并列于表5。由表中所示的相关系数取值看出,低阶傅里叶系数的取值均接近1,表明预测值取得了较好的效果。当阶数升高时,相关系数有所降低,这是由于高阶傅里叶系数对应的是荷载曲线更为细部的特征,与人体运动轨迹之间的关系更难被网络抓取。
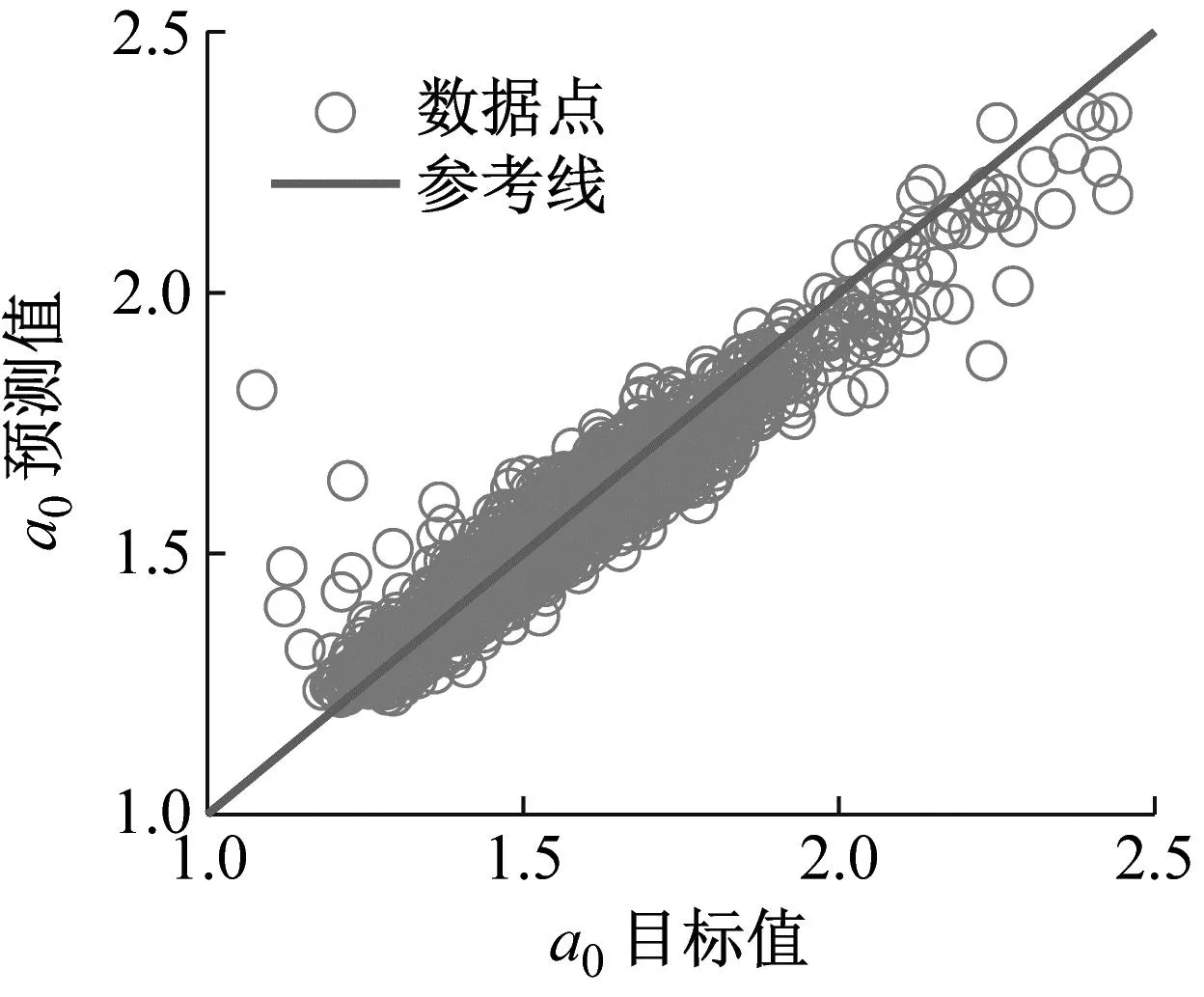
(a) a0训练结果

表5 多参数模型目标值与预测值相关系数
将训练好的网络同样应用于某一测试者连续跳跃的地反力预测并考察其时域和频域特征,其结果如图14所示。将图14与图10进行对比可以看出,采用多参数模型能够更好地描述时程曲线中的细部特征(图10(a)与图14(a)),而这一特征在频域上反映为在荷载的高频段也能够更接近真实荷载(图10(b)与图14(b))。
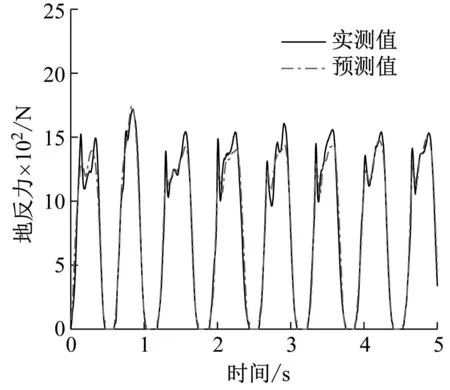
(a) 时程曲线
4 结 论
基于医学中的步态分析与三维动作捕捉系统进行跳跃荷载动力特性试验,采用深度学习中的卷积神经网络方法对人体跳跃时特征点轨迹与地反力特征参数之间的关系进行训练,实现了从人体轨迹向地反力的转换。结果表明,提出的方法可作为一种跳跃荷载的间接测量方法。在本文建立的方法基础之上,结合视频录像和计算机视觉技术,考虑人群荷载的协同状况,即可用于大规模荷载数据库的建立以及实际结构服役荷载监测。
本研究的结论主要包括:
(1) 人体运动轨迹与地反力特征参数之间存在着高维度非线性映射关系,这一关系可由卷积神经网络获取。
(2) 采用多个特征点作为输入有助于提升训练与预测效果;对于低频跳跃,由于荷载曲线的多峰特征,地反力参数的预测误差随跳跃频率的升高而降低,从约7%降低至约3%。
(3) 在对三参数模型的预测中,采用单一输入时的预测结果的平均相关系数约为0.9,而当采用多个输入时,相关系数可提升至0.95以上,说明了下肢轨迹在荷载重构中的作用。
(4) 对于多参数的傅里叶级数模型,低阶系数于人体运动轨迹具有更高的相关性。
(5) 从频域上看,对于5 Hz以上的频域分量,采用三参数模型的拟合结果具有明显误差,而高阶傅里叶模型的预测结果在时域和频域均更为贴近真实荷载。

