双轮支柱式起落架刹车振动分析与减振优化
蒋 伟,张 明,胡晓航,朱 鑫,唐立明
(1.南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016;2.南京航空航天大学 航空学院,南京 210016)
在国内外新冠疫情管控形势得到缓解和经济的不断复苏的大背景环境下,预计未来二十年,全球航空旅客周转量(revenue passnger kilometer,RPK)将以平均每年4.46%的速度递增[1]。在航空运输业发展的背后,必须看到航行安全性问题。而在整个飞行过程中,起降阶段所占的时间只有6%左右,但对应的事故发生率一直高居榜首[2]。且随着我国航空事业的不断发展,近年来涌现了众多领域的创新飞机设计型号,面对不同的着陆环境和滑跑动态性能要求,对起落架和刹车装置的结构布局形式、材料应用提出了不同的需求,这也给起落架的振动问题带来了更为严峻的挑战[3]。
飞机地面滑跑刹车时,由于跑道条件复杂性[4]和防滑刹车系统的频繁作用,会产生交变的刹车力矩作用在机轮上,影响轮胎和地面之间的结合系数和结合力,最终会引发起落架的航向振动,这种如图1所示的振动即为起落架走步/抖振。
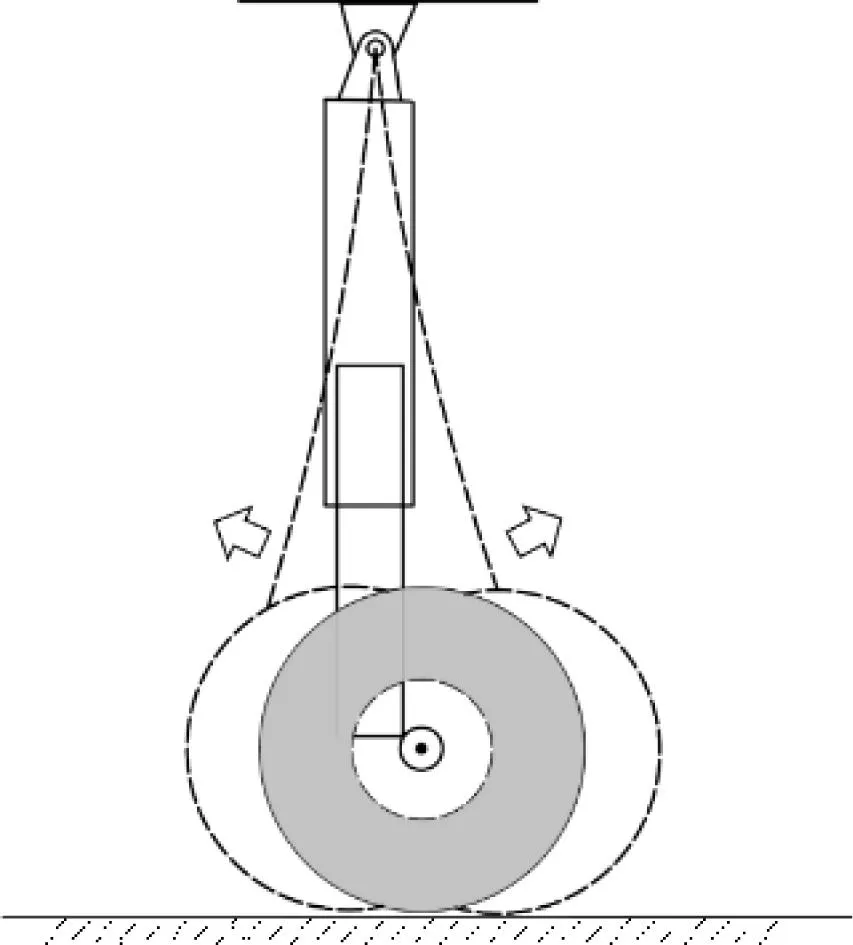
图1 起落架抖振示意图
对于起落架抖振现象的研究,国内外大致开始于二十世纪九十年代,主要通过仿真分析得到起落架抖振的参数影响规律,其中Enright[5]利用简化的起落架制动试验器具测试验证了仿真的准确性,确定制动力矩的大小对起落架抖振的影响作用。与此同时国内学者杨晓明[6]于1996年率先总结了机轮和刹车装置所引发的振动问题。随后库玉鳌[7]通过建立支柱振动周期和刹车力矩之间的定量模型,分析了刹车与起落架抖振之间的相互影响关系。张陵等[8-9]分别建立了主起落架及各元件的简单力学计算模型,将支柱和轮胎等弹性部件简化为弹簧阻尼系统,分析了起落架刚度、控制器等参数对起落架纵向抖振的影响。上述成果为飞机刹车诱导低频振动领域提供了研究基础。但迫于上述模型建立过程受计算环境影响简化较多,一定程度上偏离实际情况,进而不能准确描述飞机复杂的制动过程。
二十一世纪初期,随着虚拟样机技术的发展,国内外学者为获得尽可能接近实际情况的动态响应,开始借助于多体动力学软件来建立分析模型,Khapane[10]利用多体仿真工具SIMPACK研究了起落架抖振的稳定性问题。利用Adamas仿真工具,张明等[11]和邱东海等[12]分别建立了飞机地面滑跑起落架动力学模型,研究了不同防滑刹车控制律和刹车操纵对起落架振动的影响。尹乔之等[13]和Liao等[14]在LMS Virtual.Lab Motion中分别针对某半轴式主起落架和六轮起落架柔性问题进行了研究,分析了刹车力矩的作用幅值、频率对起落架抖振的影响。杜晓琼等[15]针对水陆两栖飞机的高支柱式起落架,对比分析了不同控制方式下的起落架振动特性和抗扰动能力。这类多体动力学软件虽具备较高的仿真精度,但建模仿真过程需要几何模型的导入,模型的网格划分,运动副的定义甚至联合仿真等众多繁琐步骤,计算效率底下,显然不能满足快速分析设计的需求[16]。而快速分析设计是现代信息技术和计算辅助水平提升的必然产物,也是现代飞机制造业界的竞争核心之一。
综上,过去研究中往往需要在模型精度和计算效率之间进行权衡,再通过仿真分析方法,来得到抖振参数影响规律,指导相关设计工作,近年来多目标优化方法在各类领域得到了广泛的应用[17-18],但较少有研究针对起落架系统设计提供参数优化方法。本文将首先建立包含机械振动、液压传动、热力耦合、动力学分析等多个专业学科领域的整机六自由度地面运动数学模型,由于模型保留了起落架和机体的主要自由度,并对影响航向振动的关键性部件进行了细化建模,因此能将其用于描述飞机复杂的地面制动滑跑运动过程。其次,利用分析模型进行刹车控制律的参数影响分析。最后,结合抖振影响规律和数学建模方式所提供的高效计算手段,对液压刹车系统的相关参数进行了优化设计,并在不同着陆工况下检验优化方法的有效性,为抖振机理研究和起落架系统设计提供参考。
1 飞机地面滑跑刹车动力学建模
为满足刹车系统与起落架耦合振动快速分析优化设计的核心要求,细化和刹车诱导振动相关构件的建模。模型基本假设为:
(1) 飞机处理为弹性支撑质量和非弹性支撑质量两部分,其中前者为缓冲器支撑质量,后者为活塞杆以下结构等效质量。
(2) 起落架支柱考虑航向、侧向、扭转三个方向自由度,气动力集中作用于飞机质心。
1.1 六自由度机体动力学建模
为全方位模拟飞机地面滑跑着陆动态特性,建立图2所示的机体六自由度运动模型。
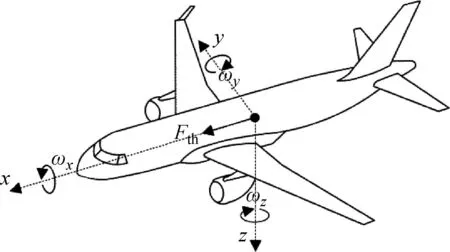
图2 机体动力学模型
在惯性坐标系下建立机体质心的平动方程
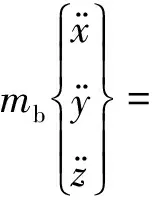
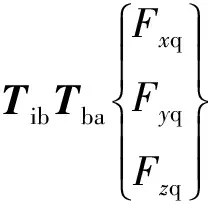
(1)
在机体坐标系下建立质心的转动方程
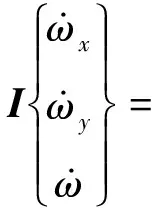
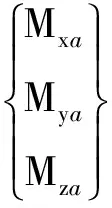
(2)
式中:mb为飞机质量;Fth为飞机剩余推力;[FxjFyjFzj]T为支柱对机身作用力矢量;[FxqFyqFzq]T为气动力矢量;[MxjMyjMzj]T为起落架作用机身力矩矢量;[MxaMyaMza]T为气动力矩矢量。
1.2 起落架支柱动力学模型
建立如图3所示的起落架支柱动力学分析模型,将非弹性质量集中于起落架支柱与轮轴连接点处,在惯性坐标系下非弹性支撑质量的平动方程由式(3)确定。
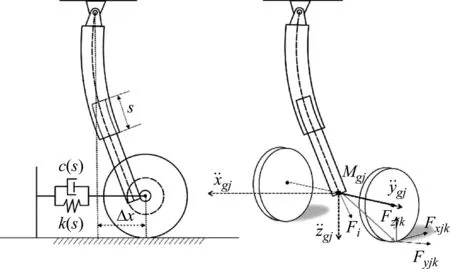
图3 双轮支柱式起落架动力学分析模型
(3)
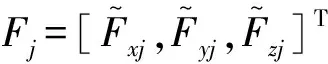
考虑缓冲器压缩量对航向刚度的影响,变刚度支柱动力学模型的起落架支柱的各向力计算表达式为
(4)
(5)
式中:Tsjb为机体坐标系到支柱坐标系转换矩阵;Δx、Δy为支柱航、侧向变形量;faj为空气弹簧力;fhj为油液阻尼力;k(s)为刚度位移函数;k0、kmax分别为缓冲器无压缩和满行程时对应支柱等效刚度值;c(s)为阻尼速度函数,受支柱压缩量影响;ε0为结构阻尼系数;ml为起落架结构质量。
1.3 考虑材料摩擦特性的刹车装置模型
刹车装置主要功能为将液压系统作用的刹车压力转化为刹车力矩,并作用于静盘上使动静盘相互挤压摩擦产生热量,进而消耗滑跑动能,如图4所示。
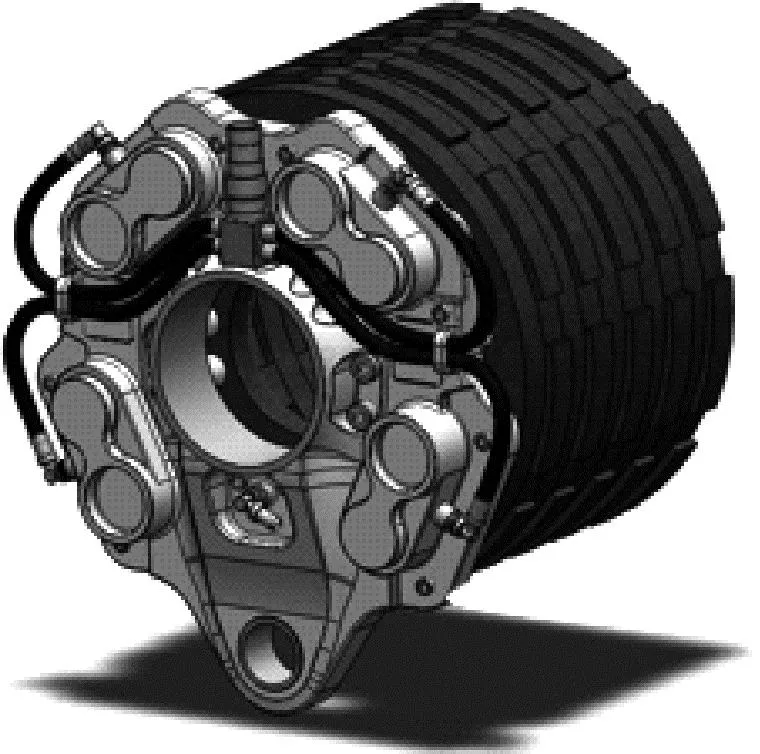
图4 刹车装置模型
环形摩擦面内刹车力矩具体计算公式为
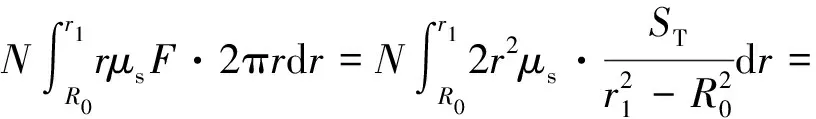
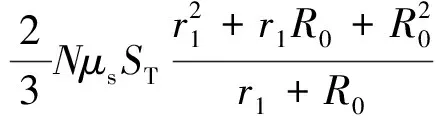
(6)
ST=(P-P0)·S·n
(7)
式中:r0为静盘内径;r1为静盘外径;R0为动盘内径;R1为动盘外径;P为刹车压力;P0为预紧压力;S为液压作动筒面积;n为作动筒数量;μs为刹车盘面摩擦因数。受盘面材料属性影响,具体计算公式为
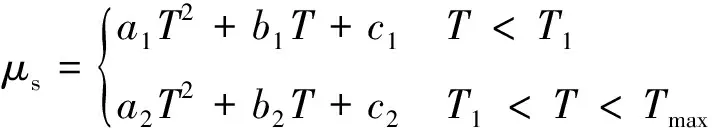
(8)
式中:ai,bi,ci为碳基刹车盘材料相关系数;Tmax为材料极限温度;T1为材料最佳温度。
盘面温度T的求取依赖于所建立的热力耦合模型[19],如图5所示,主要分为生热、散热、温升三大部分。
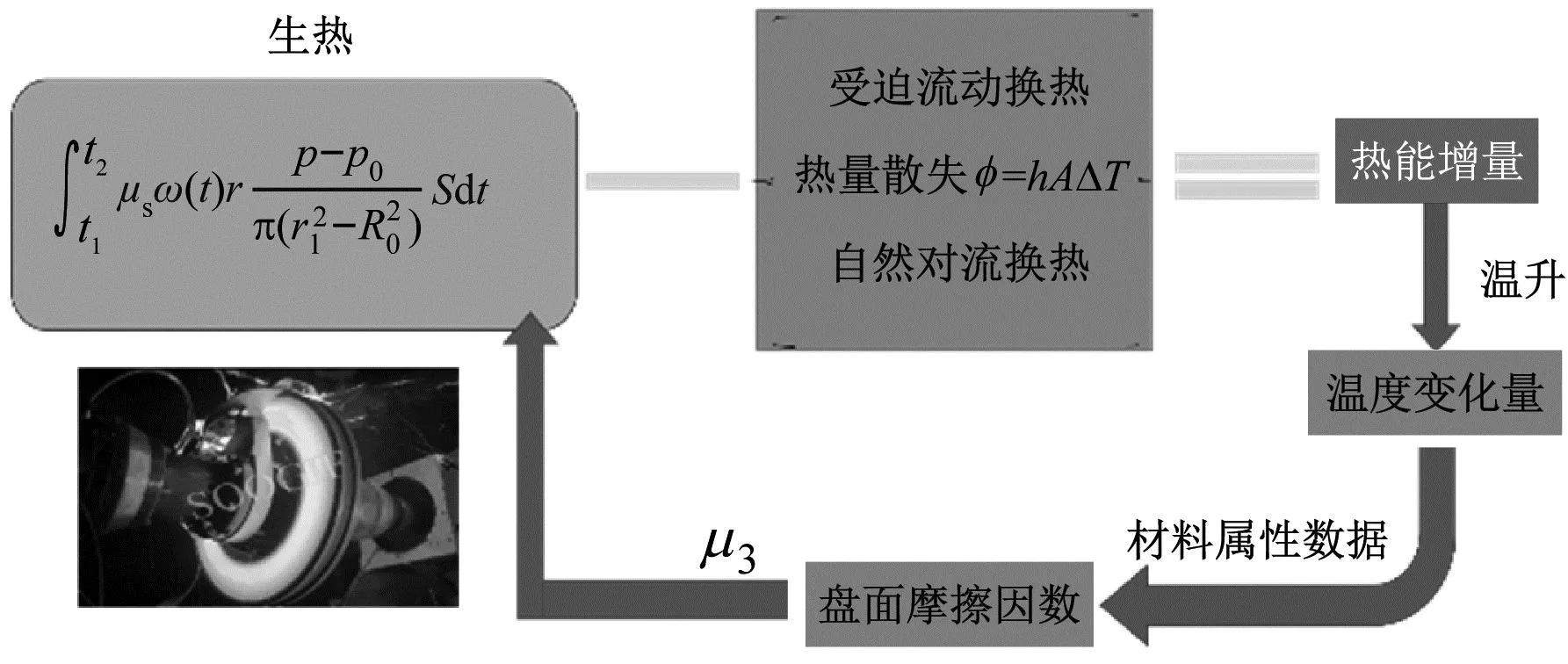
图5 刹车盘面热力耦合模型
(1) 生热模型
Wb=μsPVw(r,t)
(9)
式中,Vw(r,t)为接触点上的线速度。考虑迟滞压力下的摩擦面热流密度计算公式为
(10)
(2) 散热模型
摩擦产生的热量主要通过对流换热和热辐射两种形式耗散,由于刹车装置封闭性原因,实际热辐射损失热量较少,对流换热的能量损耗热流密度计算方式为
qs=hs(T-T0)
(11)
hs=Nuλ/l0
(12)
式中:T0为环境温度;hs为表面热换流系数;λ为流体传导系数;L0为固态壁面特征尺寸;Nu为努谢尔特数。
(3) 温升模型
由热量传递分配关系,刹车盘面摩擦所生成的热量去除对流换热能量损耗后,剩余部分用于盘面温升,单位时间内系统温度增量为
(13)

(14)
式中:Qp为刹车装置系统内能;mp为刹车盘质量;Cp为刹车盘材料比热容。
1.4 机轮和液压刹车控制系统模型
(1) 机轮动力学模型
机轮模型采用航空轮胎中普遍使用的TR-R-64半经验模型,机轮转动方程为
(15)
式中:Mj为地面结合力矩;Jr为机轮转动惯量;Rg为机轮滚动半径;μx为纵向滑动摩擦因数,采用经典魔术公式得到。
μx=Dsin(C·arctan(Bσ))
(16)
(17)
式中:B为曲线形状因子;C为刚度因子;D为峰值因子,其取值与道面状况相关,σ为机轮滑移率;vx和vw为飞机和机轮航向速度。
(2) 刹车控制律模型
滑移率PID刹车控制系统原理如图6所示。系统力图将实时滑移率控制在结合系数最大值对应的最优滑移率附近,以提高系统刹车效率。本文中四个主轮刹车控制通道相互独立,暂不考虑差动刹车等纠偏控制策略。
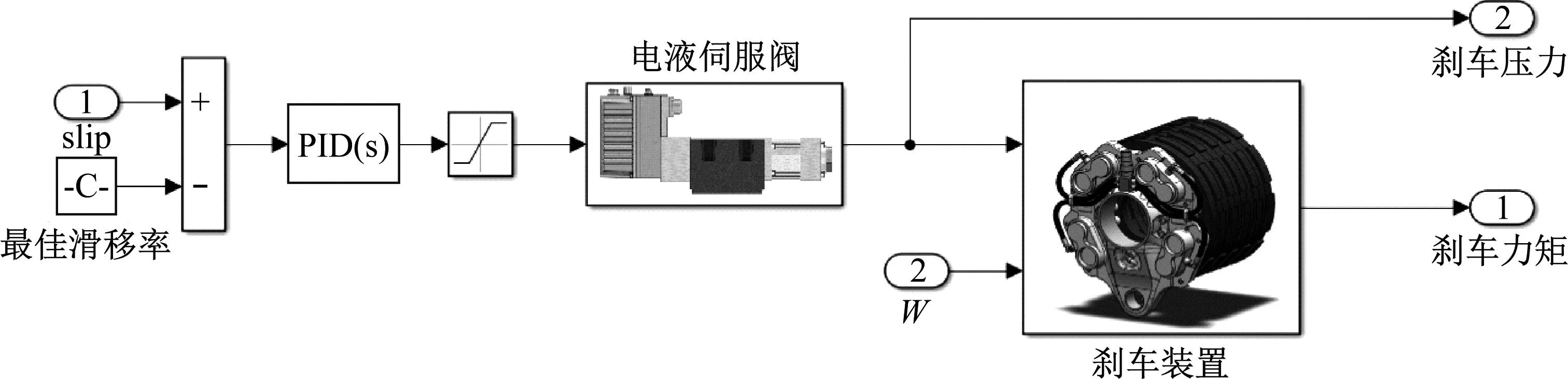
图6 滑移率PID刹车控制系统原理
控制器输入为实时滑移率和预设的最佳滑移率差值,输出防滑控制电流控制刹车压力来调节机轮速度形成闭环。防滑电流输出为
(18)
式中:I为防滑输出电流;Kp为比例系数;Ki为积分系数;Kd为微分系数;Δσ为滑移率实时误差项。
(3) 电液伺服阀模型
电液伺服阀作用为将控制盒的防滑电流信号转化为刹车压力,在实际使用中,其模型可简化为下面二阶传递函数形式
(19)
式中,ωn、ε分别为伺服阀固有频率和相对阻尼系数。管道模型可描述为如下惯性环节
(20)
2 控制器参数对起落架抖振影响分析
2.1 整机仿真分析模型搭建
本文所建立的飞机地面运动动力学模型涉及到部分强非线性系统,以及坐标系矩阵转换等复杂数学计算环节,直接用Simulink基本模块搭建过于繁琐,增加建模工作量的同时还易出错,而S函数可以轻松解决状态方程计算、数值迭代等工作,适用于本文中的复杂的飞机地面滑跑动力学建模过程。机体动力学S函数内部的数据交换结构,如图7所示。
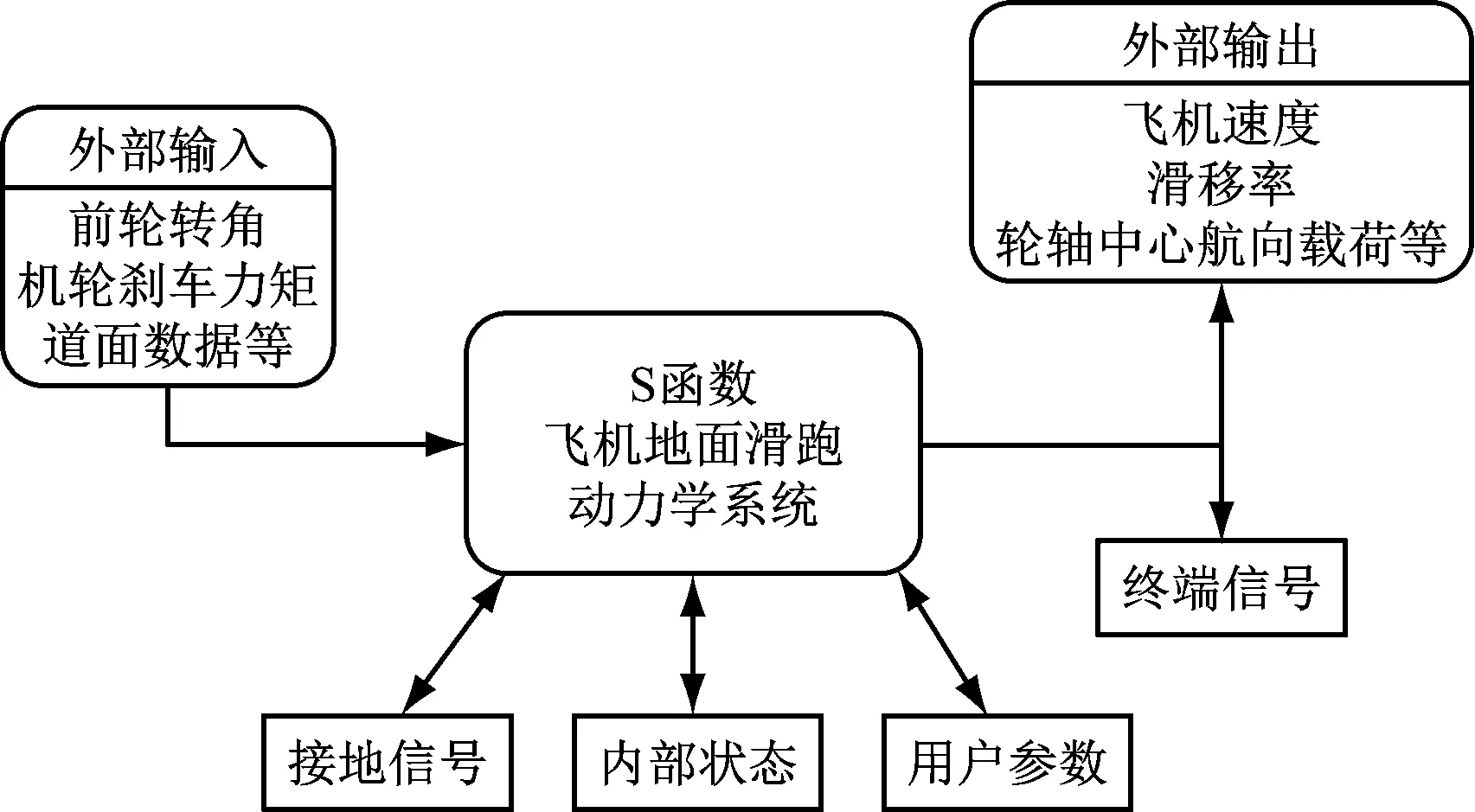
图7 S函数和外部数据交换结构
依据各自模型特点将所建立的数学模型在Simulink中进行集成,搭建了如图8所示的总体模型用以后续研究分析,主要包含:整机地面运动的机体动力学S函数、独立通道控制的液压刹车控制系统、跑道模型等。
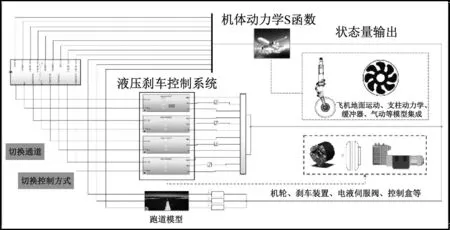
图8 Simulink总体模型
2.2 刹车控制律参数影响分析
对于影响起落架抖振程度的两类关键因素结构固有特性和防滑刹车系统激励而言,前者受设计要素的影响调整区间受限,所以本节中主要进行刹车控制律相关参数的影响分析,以支撑后续优化设计分析。对滑移率PID刹车控制律的比例、积分、微分系数进行参数影响分析,结果如图9~图11所示。
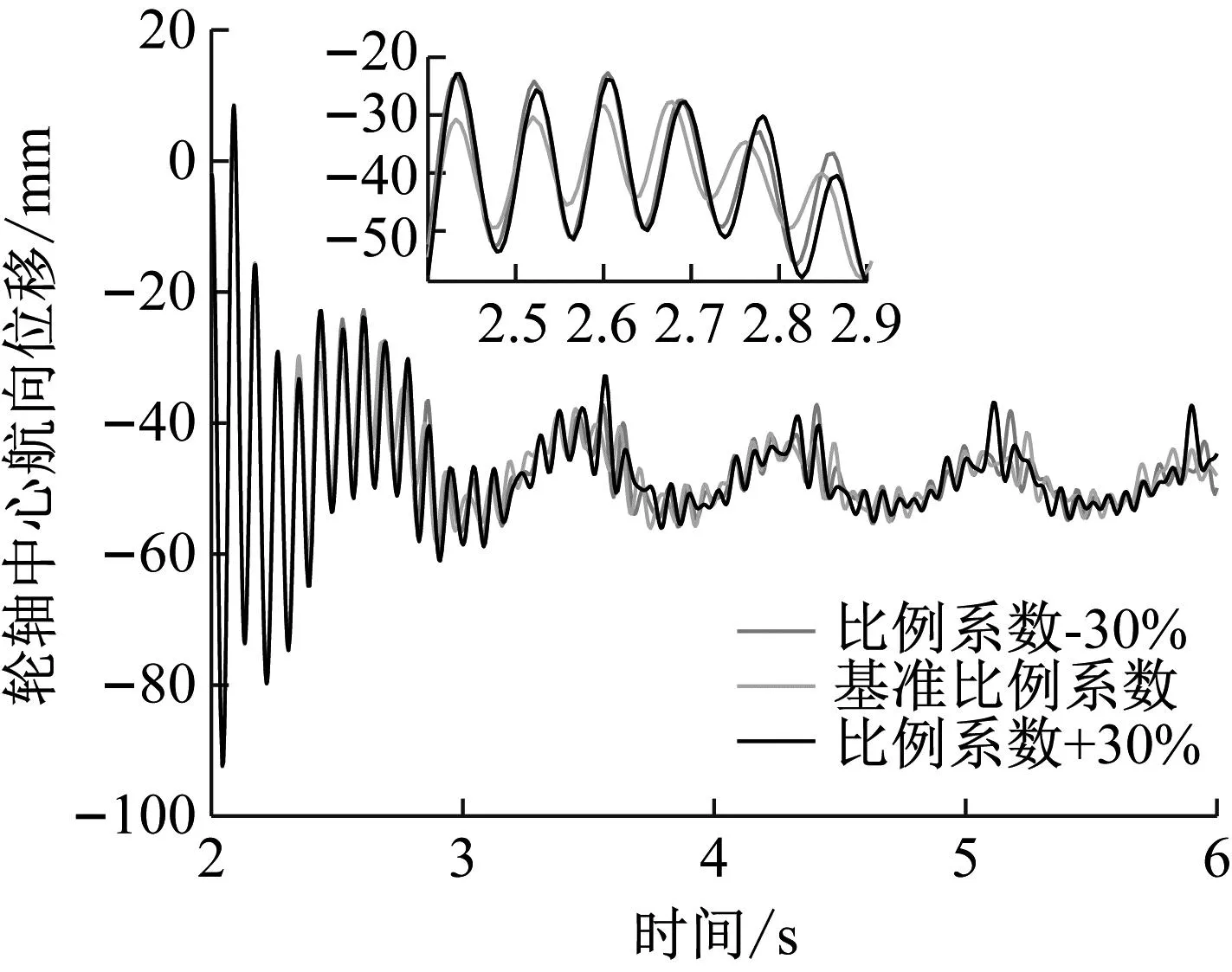
图9 不同比例系数下轮轴中心航向位移
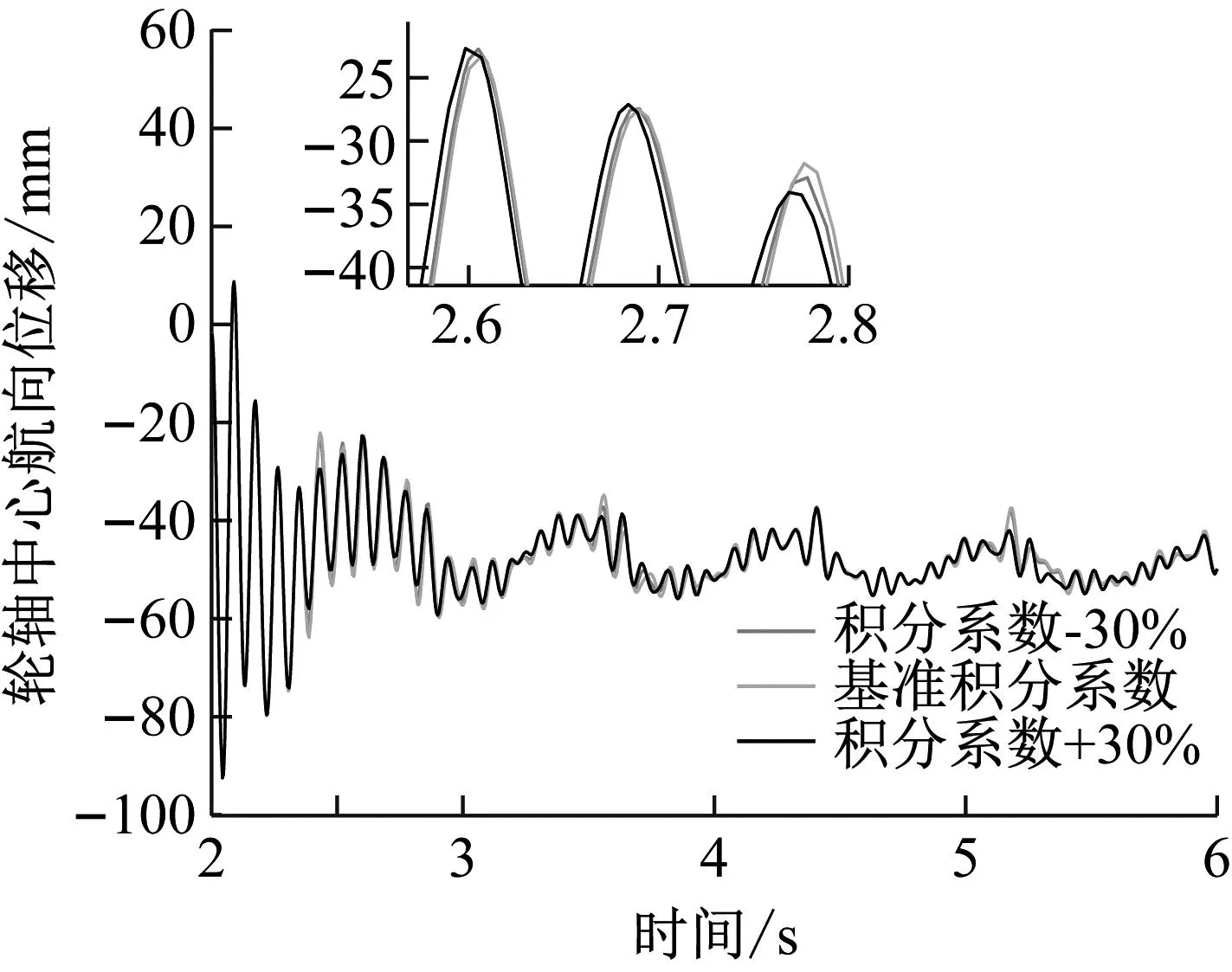
图10 不同积分系数下轮轴中心航向位移
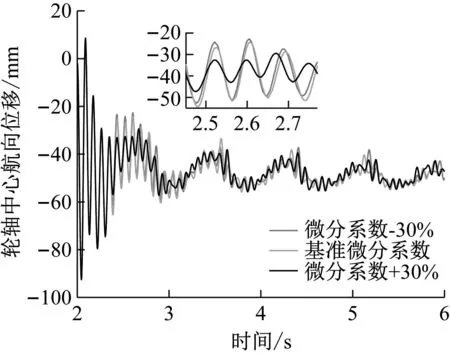
图11 不同微分系数下轮轴中心航向位移
结果分析:从左主起落架轮轴中心处的航向位移对比图可以看出,PID控制参数均会对起落架抖振程度产生影响,后续若无特殊申明,轮轴中心运动状态监测量均选用左主起落架相关数据。随比例系数的增大,轮轴中心航向位移总体波动幅度变大,原因在于增大比例系数能使系统反应灵敏,调节速度加快,进而使轮胎与地面间时刻拥有相对较高的摩擦因数,轮胎航向受载增大,且随之而来的超调量增大,动态性能变坏等问题,促使起落架航向载荷波动幅度增大,进而加剧振动。积分系数的改变能影响稳态误差,但由于系统响应较快,这一参数变化给抖振现象带来的影响不太明显。随微分系数的增大,控制系统超调量减小,机轮滑移率波动幅度减小,进而使机轮地面结合力波动减小,起落架抖振程度减缓。
3 起落架减振参数多目标优化
类似于本文第2章中的起落架抖振参数影响性分析研究,可以为研究人员提供大体减振思路,但如何在短时间内获取满足性能需求的最优参数值是刹车振动问题的研究重点,由此本章中将基于NSGA-Ⅱ算法进行起落架减振快速优化设计。
3.1 优化变量和约束条件
对于液压刹车控制系统参数而言,主要考虑电液伺服阀和控制器两大关键部件参数优化。电液伺服阀能将微小电流信号增益为数十兆帕的刹车压力,如图12所示其固有频率的改变会对刹车压力的动态响应产生较大影响,进而影响防滑控制效果和起落架抖振程度。
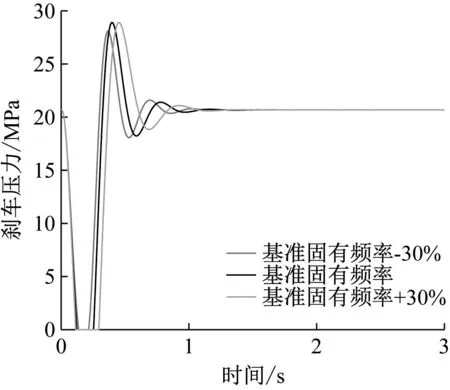
图12 不同电液伺服阀动态响应特性
结合2.2节中控制律参数对起落架抖振影响分析,将优化变量确定为:电液伺服阀阻尼比ε、固有频率ωn、控制器比例系数Pp、积分系数Pi、微分系数Pd。
(21)
在满足仿真精度和实际参数设计过程情况下,优化变量对应具体约束条件为
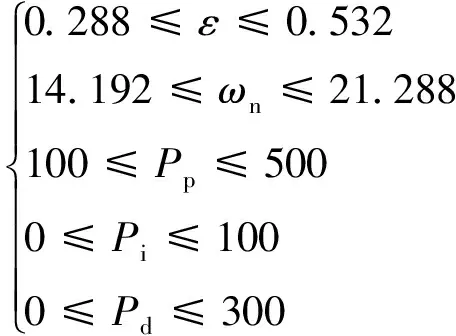
(22)
3.2 目标函数
优化目的是通过调整液压刹车控制系统参数,来缓解起落架抖振程度,和提高刹车效率的效果。对于前者,RMS值是最有用的振幅度量,因为它既考虑了波的时间历程,还给出了和能量直接相关的振幅值,从而与振动的破坏能力直接相关。其计算表达式为
(23)
振动峰值A等其余相关振动量化参数的定义如图13所示。
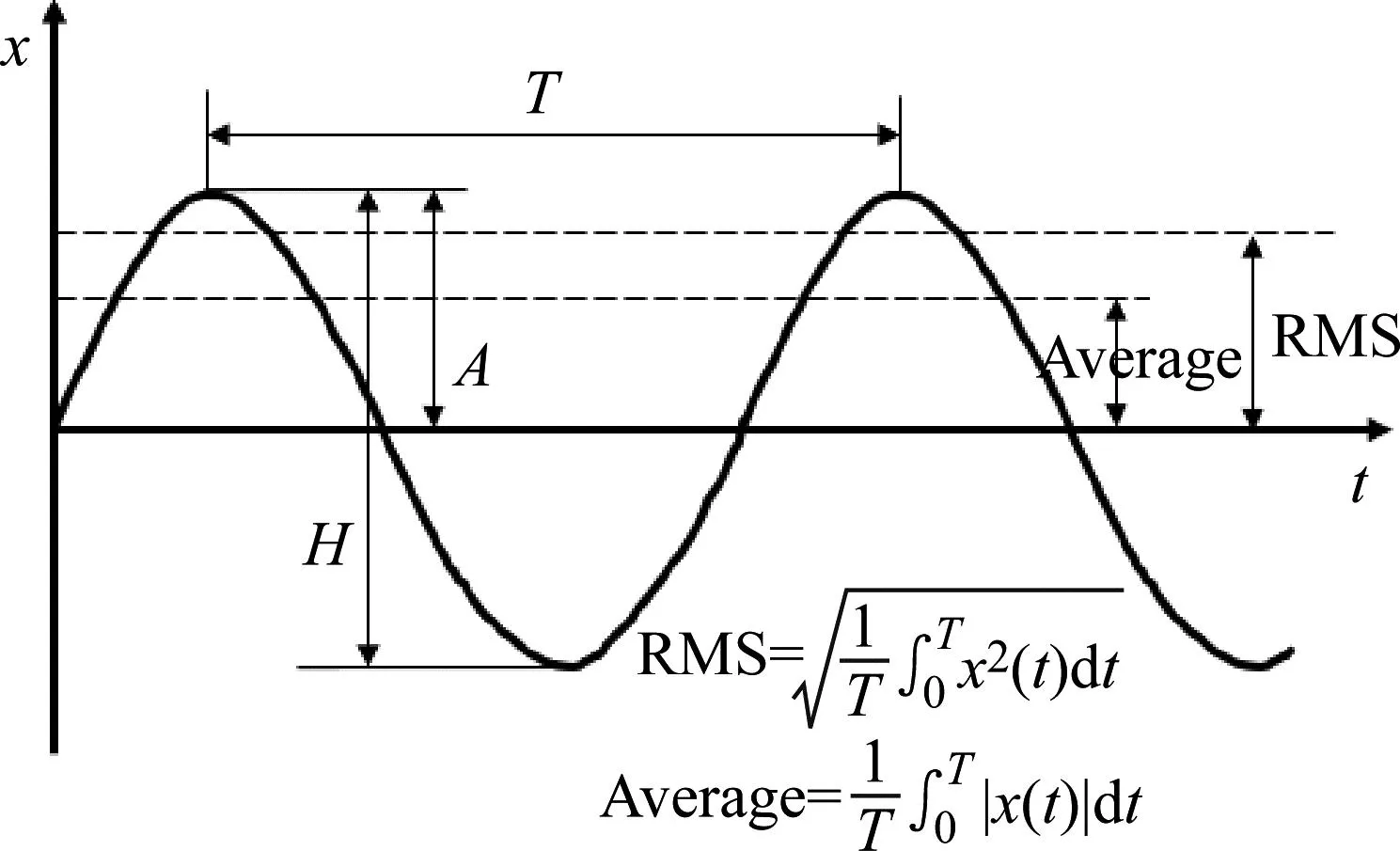
图13 振动量化指标定义
选用起落架轮轴中心点处的航向加速度的RMS值来评价起落架耦合振动态势,即:
(24)
式中:T为仿真时间;a(t)为振动加速度响应。
优良的刹车系统在各种情况下能安全可靠的工作,轮胎磨损均匀,系统工作稳定。而结合系数效率的高低是衡量刹车系统设计好坏的标准之一,其中结合系数效率指如图14所示的在一定时间内结合系数参数的实际值占理想值的平均百分比,其能用于刻画飞机刹车系统的效率高低。
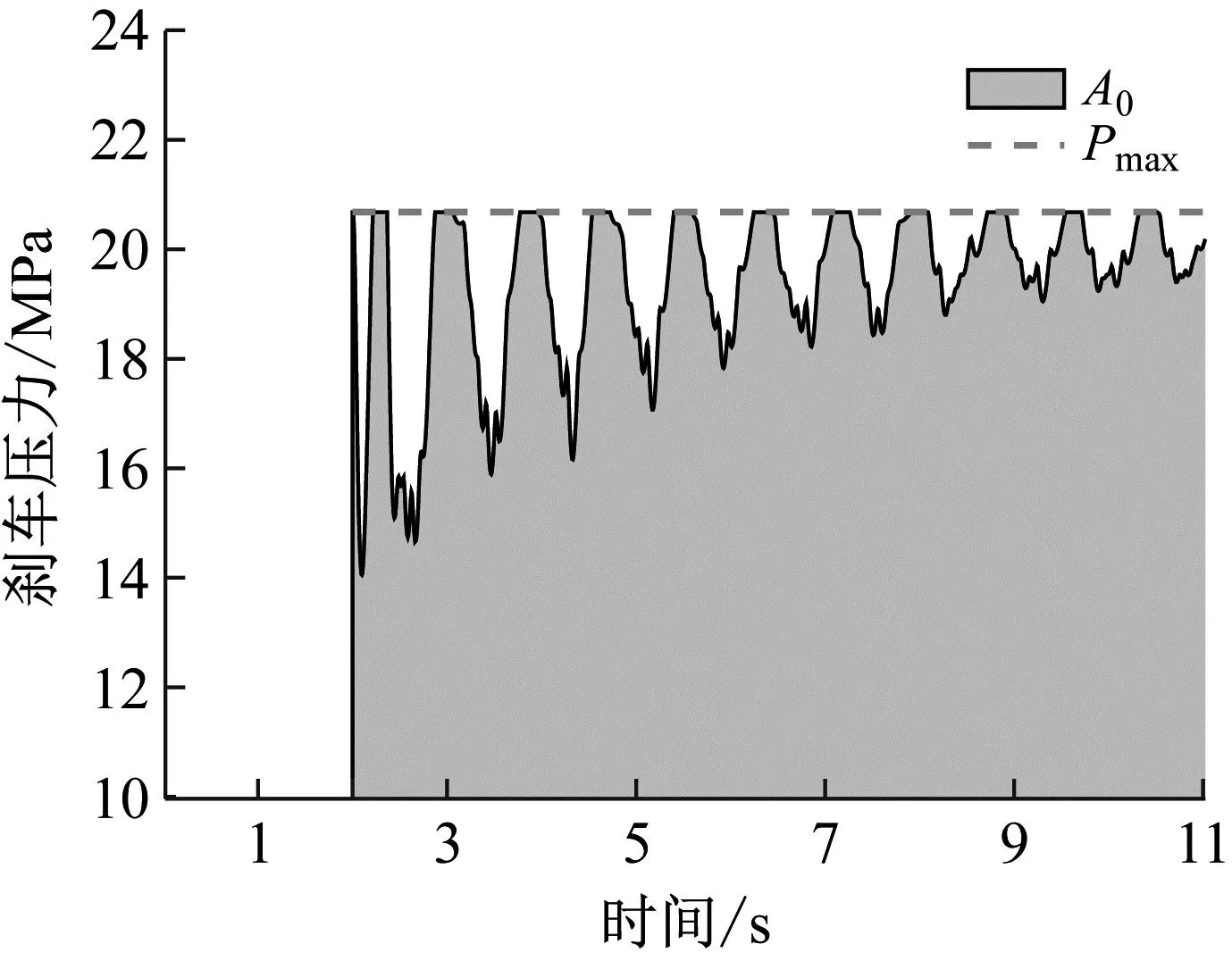
图14 结合系数效率定义
ηb=S曲/S直×100%
(25)
式中:S曲为图8中阴影部分面积;S直为结合系数变化迹线包线与坐标轴所围面积。
3.3 多目标遗传优化算法实现
NSGA-Ⅱ算法是Srinivas 在NSGA 的基础上提出的,其具备以下特点:① 采用的快速非支配排序算法,使其相比于NSGA算法的计算复杂度大幅降低;② 精英策略的引入扩大采样空间,以防最优解的遗漏;③ 采用拥挤度和拥挤度比较算子确保个体扩展到整个最优解集,维持种群多样性。综上,这一算法具备优良的运算速度和鲁棒性,符合本文优化设计的需求。
基于多目标遗传优化算法的起落架结构减振优化过程如图15所示。首先在Matlab中编写NSGAⅡ程序来生成关于5个优化变量的初始种群,将变量值在工作区间进行定义。其次,调用Simulink地面滑跑刹车动力学模型仿真得到对应种群目标函数值,记录前后两代种群中的精英个体。最后,通过交叉变异等遗传算子操作得到下一代种群,直至满足迭代停止条件,得到影响起落架抖振程度的液压控制系统优化参数的Pareto最优解集。
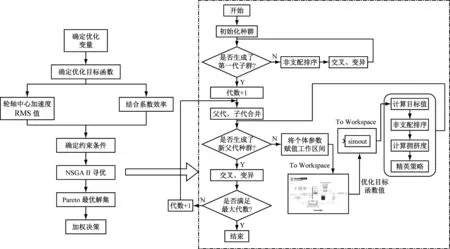
图15 基于Simulink的多目标遗传优化算法实现
NSGAⅡ算法设置中取交叉算子为 0.7;变异算子为 0.3;种群大小为 100;最大进化代数和停止代数为 10;仿真部分关键参数设置中令初始质心离地高度5 m;初始着陆速度50 m/s;初始着陆质量77 000 kg;初始机体俯仰角0.034 9 rad。
(1) Pareto最优解集
迭代20代后算法停止,优化后的Pareto最优解集和对应的优化变量取值如表1所示。
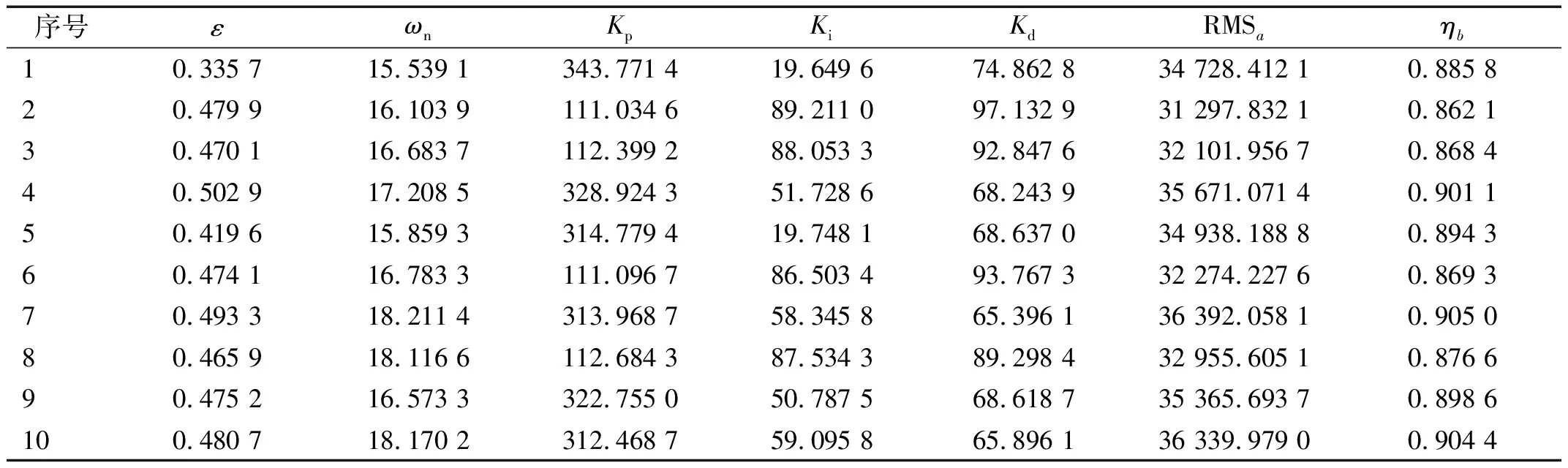
表1 多目标优化参数最优解集取值
(2) TOPSIS折衷最优解
引入TOPSIS决策方法从众多可行解中选取折衷解,以方便后续优化前后结果对比分析,TOPSIS决策方法,又称优劣解距离法,是一种根据评价对象和理想最优目标的欧式距离远近进行优劣排序的方法,针对本节中的Pareto解集决策问题,其具体实现步骤为:
步骤1指标正向化
为避免加速度RMS值(成本型)和结合系数效率(效率型)两种指标带来的评价尺度混乱问题,进行正向化处理
RMSi=max{RMS1,RMS2…RMSn}-RMSi
(26)
步骤2指标标准化
为消除评价指标量纲差异,进行归一化处理
(27)
步骤3欧氏距离计算
定义欧式距离di用以描述评价对象与理想解或非理想解的距离远近。
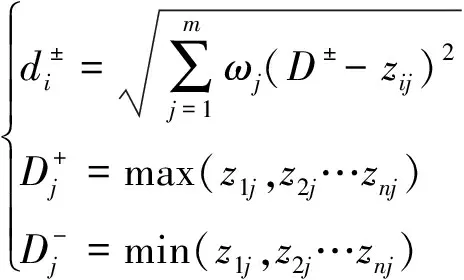
(28)
式中:ωj为各目标权重,采用主观赋权法取加速度RMS指标权重ω1=0.5,结合系数指标权重ω2=0.5。
步骤4综合评价指标计算
TOPSIS方法的决策思想为综合考虑评价对象所处的位置与理想点和非理想点的距离远近。
图16所示的几何关系,定义相对接近度Yi计算表达式为
(29)
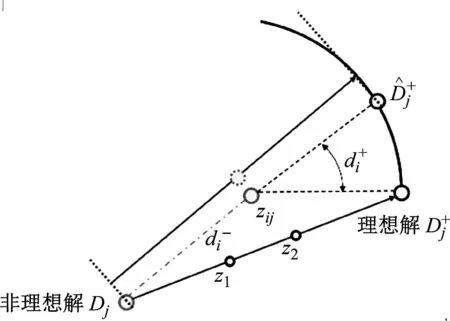
图16 综合评价指标几何示意图
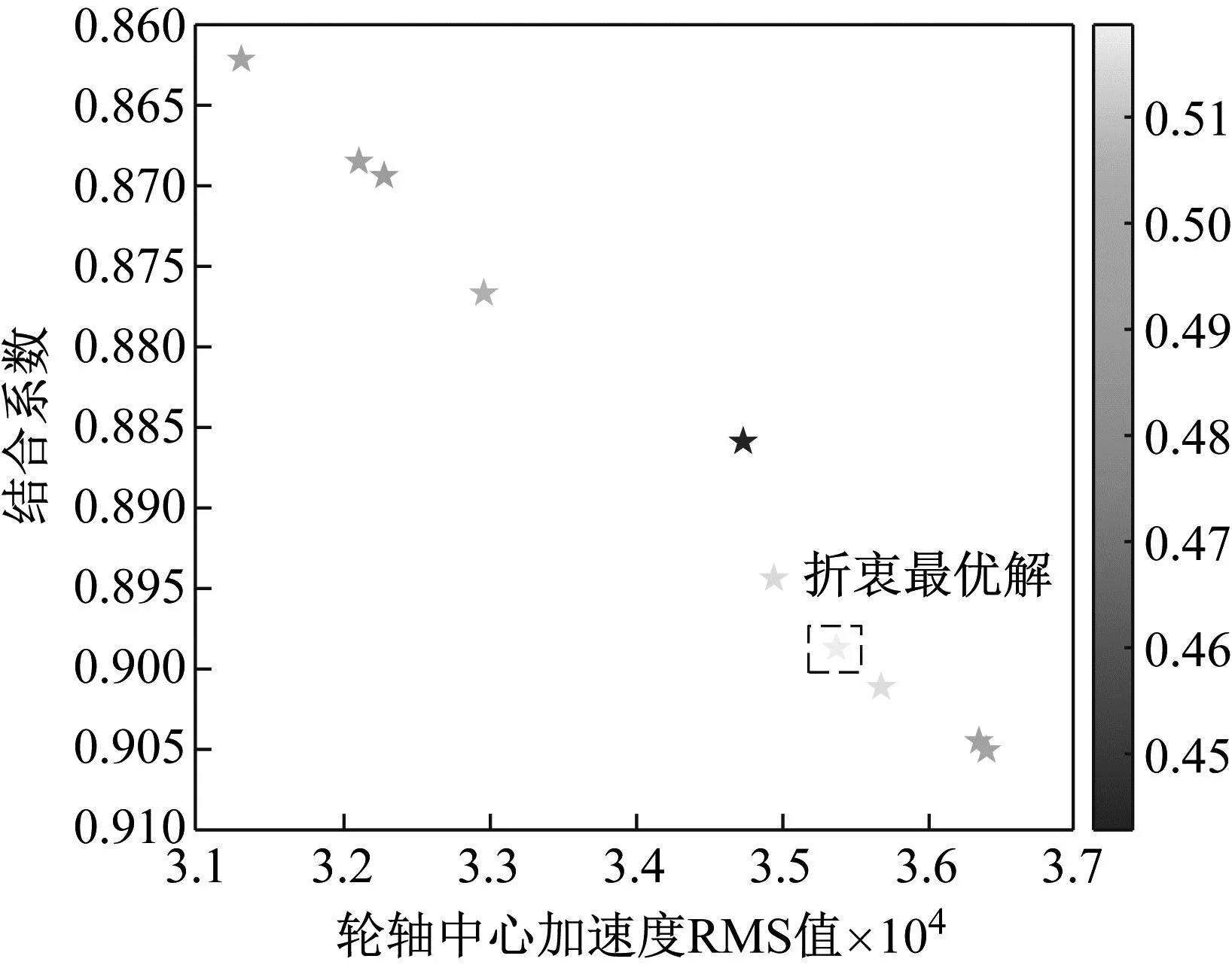
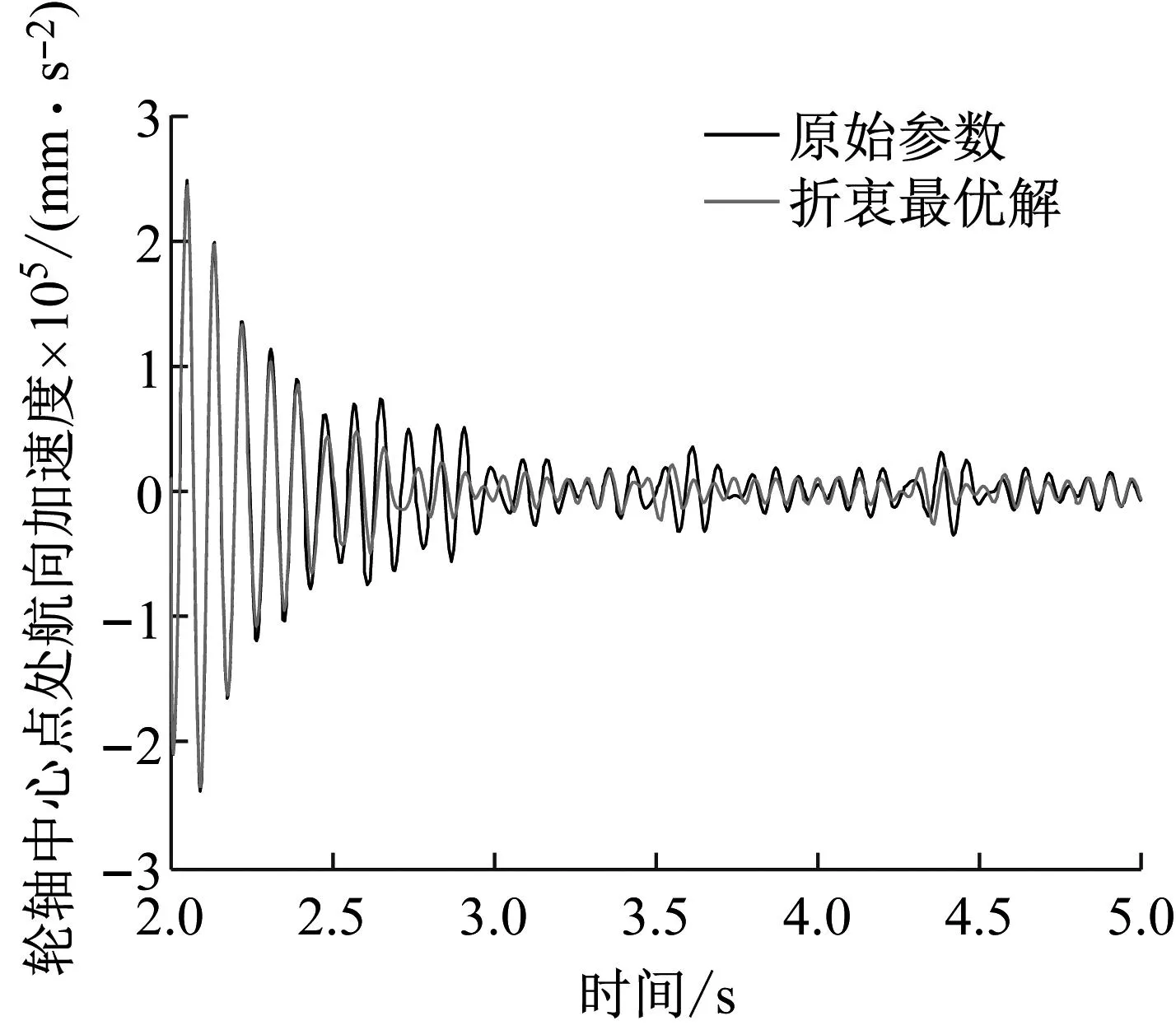
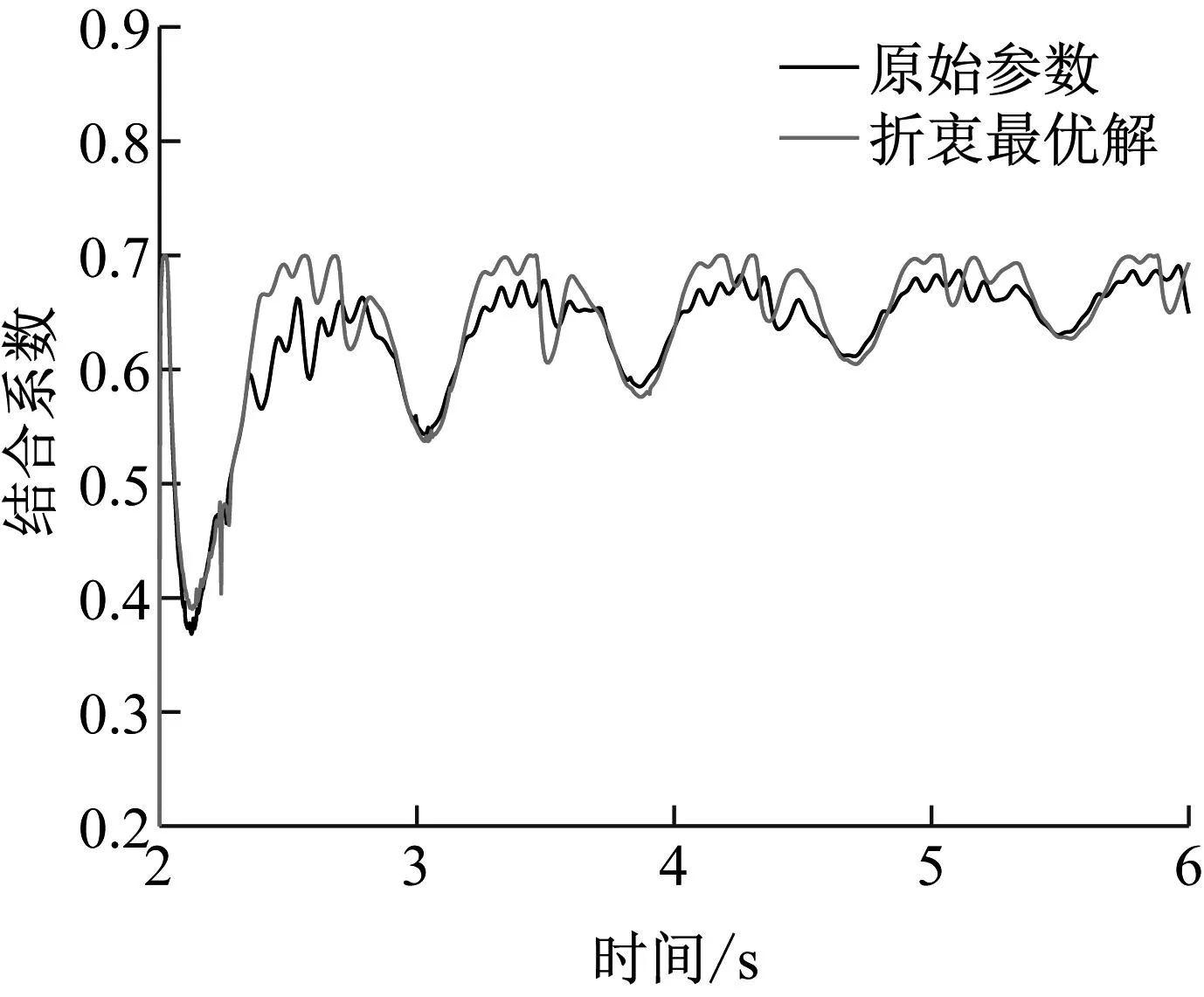
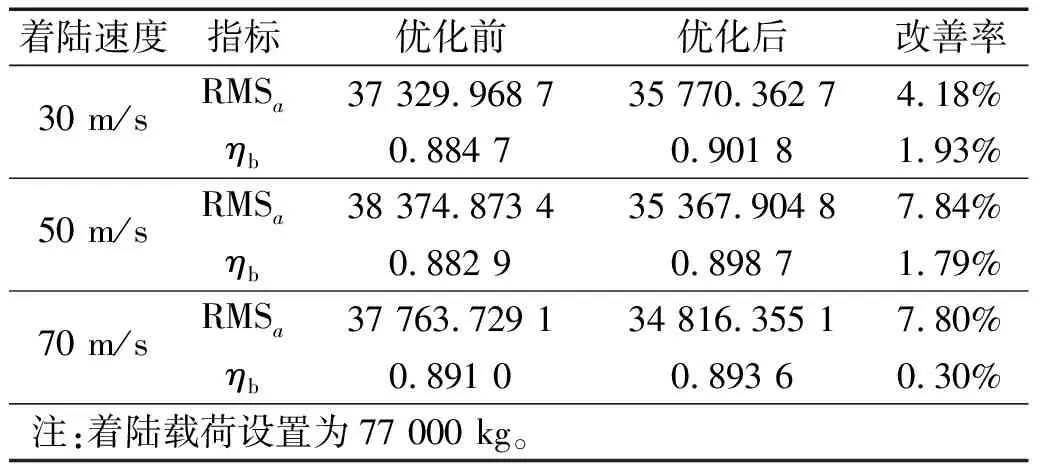
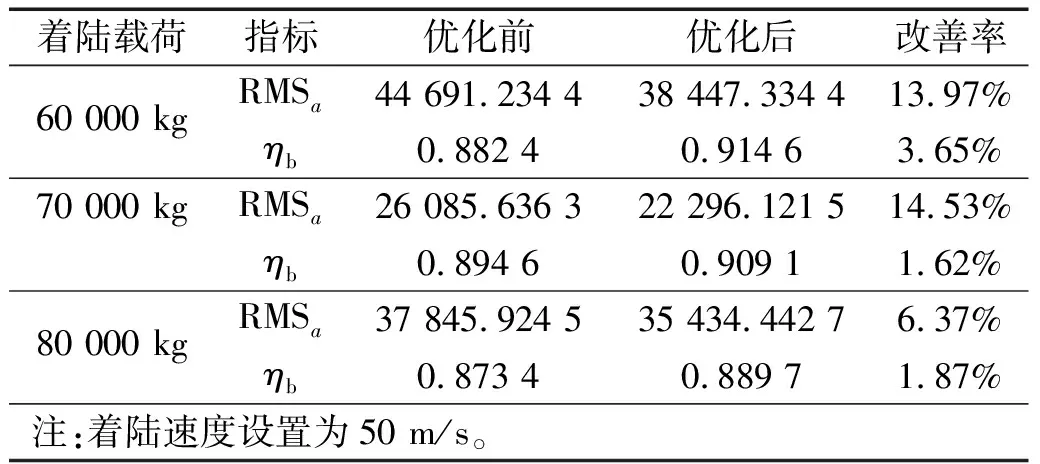
式中:0 表2 TOPSIS最优决策数据表 结合综合评价指标进行Pareto最优前沿图绘制如图17所示。 图17 Parero最优前沿图 Pareto最优前沿面中,结合系数效率的变化区间为[86.21%,90.50%],轮轴中心加速度RMS值变化区间为[31 297.832 1,36 339.979 0],最大综合评价指标对应的折衷最优解为 X=[0.475 2 16.573 3 322.755 0 50.787 5 68.618 7] (30) (3) 折衷最优解验证 将飞机以50 m/s的初始着陆速度降落在平整干跑道上,对比分析轮轴中心处的航向加速度和结合系数变化,结果如图18、图19所示。 图18 轮轴中心航向加速度对比 图19 地面结合系数对比 2 s时刻启动刹车后,轮胎所受地面结合力急剧上升,带来轮轴中心处的航向振动,但随机轮滑移率的控制趋于平稳,航向振动加速度逐步衰减。 由图18和19可知,在优化后的液压刹车控制系统参数下,轮轴中心点处的航向加速度幅度得到有效衰减,这说明优化方案对起落架的航向振动减缓起到良好的效果。与此同时,从结合系数变化对比图上看,优化后的方案能提高地面给轮胎的结合系数,一定程度上增大刹车效率。 为了验证优化方案对其它工况的减振适应能力,在折衷最优解下进行了不同初始着陆载荷和速度下的滑跑动态性能仿真分析,结果如表3、表4所示。 表3 不同着陆速度下优化结果对比 表4 不同着陆载荷下优化结果对比 从表3和4可以得到结论:即使面对不同着陆工况,优化后的方案均能有效降低轮轴处的航向加速度RMS值,并增大结合系数效率,加速度RMS值最大降幅达到14.53%;结合系数效率最大增幅为3.65%。这说明优化设计后的参数面对现代飞机复杂的着陆环境具备较高的减振适应度,能在提升刹车效率的同时有效减缓起落架抖振,进一步验证了所提出的快速优化设计方法的可靠性。 为了研究针对飞机刹车诱导低频抖振的减振快速优化设计方案,在细化关键构件的建模考虑上建立了飞机着陆刹车地面运动六自由度数学模型,并在Simulink中搭建了对应的模型用于仿真分析。通过对模型进行 仿真和减振优化设计得到以下主要结论: (1) 刹车控制律参数能一定程度影响到起落架的抖振程度,主要原因在于PID控制器的各项参数能影响机轮滑移率的控制效果,进而影响到地面结合力的大小和起落架航向振动幅度。 (2) 本文针对所研究的双轮支柱式起落架结构,提出一种基于多目标遗传优化算法的减振快速优化设计方法,仿真结果表明:优化后的液压刹车控制系统参数方案能在提高刹车效率的同时有效减缓起落架抖振程度,验证了快速分析设计方法的有效性。此外,通过不同着陆工况下的仿真结果验证了优化方法的可靠性,表明所提出的模型和优化设计方案的良好工程应用价值。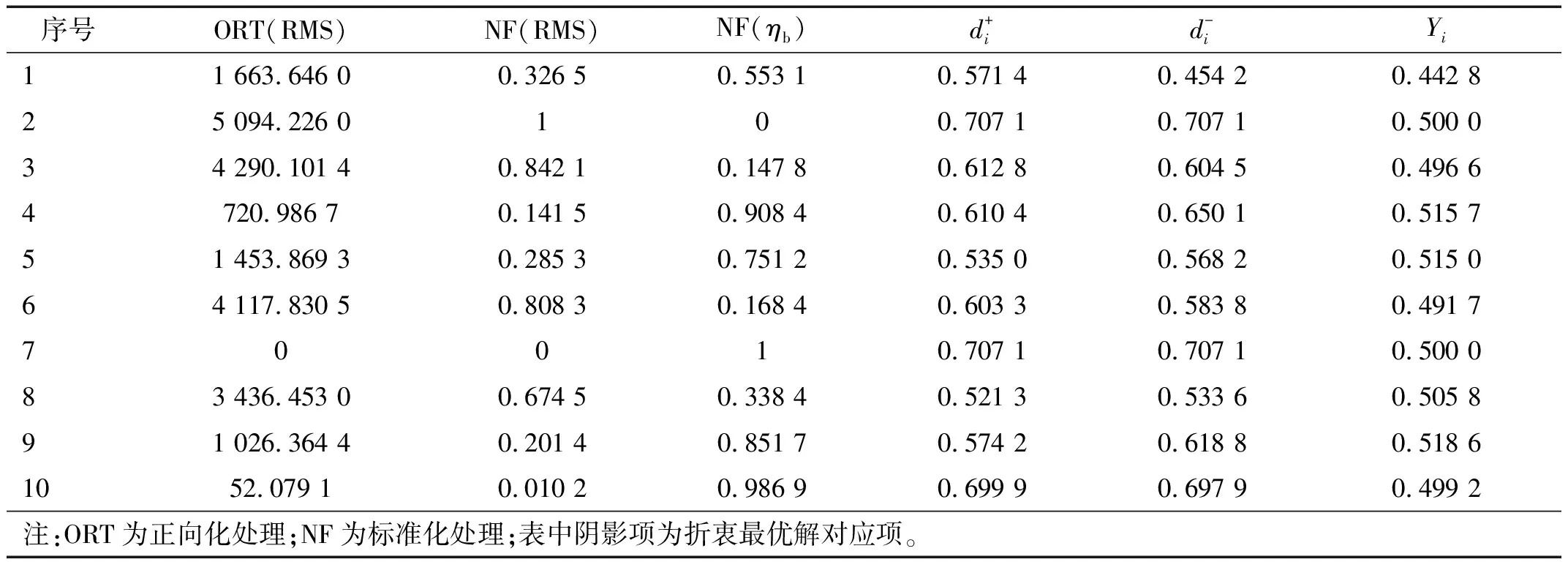
4 结 论

