海底长周期地震动预测模型:以日本相模湾海域为例
田 浩,胡进军,谭景阳,靳超越,刘名吉
(1.中国地震局 工程力学研究所,哈尔滨 150080; 2.中国地震局 地震工程与工程振动重点实验室,哈尔滨 150080; 3.华中科技大学 土木与水利工程学院,武汉 430074)
近年来,海域地震频发,2010年智利Mw8.8级海底特大地震造成大量房屋倒塌以及人员伤亡,2011年东日本Mw9.0大地震及引发的海啸和核泄漏,造成2万余人死亡或失踪,并造成了重大的经济损失[1]。海域地震动特征复杂、影响因素众多。但是海域地震动预测模型及长周期地震动特征目前研究较少。海洋工程的自振周期普遍较长,在长周期(T≥1.0 s)地震动作用下易产生共振,因此在海洋工程的抗震设防中需考虑长周期地震动影响。
研究表明,海域与陆域地震动特征存在差异,震源类型、传播路径、场地以及海水和海底沉积物等因素是造成这种差异的主要原因[2-7]。胡进军等发现,在假定场地平整的条件下,海水对S波的竖向成分在P波共振频率附近有明显的削弱作用。Dhakal等[7]3257发现在震源距200 km范围内海域和陆域地震动的峰值加速度(peak ground acceleration,PGA)无较大差异,但海域地震动峰值速度(peak ground velocity,PGV)较陆域大。Zhang等[8]研究发现,对于同一地震事件,在震中距相同的前提下,海域地震动的PGA明显大于陆域地震动PGA,导致这种差异的原因是海底沉积物的放大作用;此外,海域地震动竖向与水平向PGA比值较陆域地震动大。Chen等[9-10]利用K-NET台网的海域地震动记录,分析了竖向与水平反应谱比,发现当周期较小时,海域地震动的反应谱比远小于陆域地震动。Dhakal等[11]分析了海域地震动作用下S波的水平与竖向谱比,发现在强震作用下,海域地震动会引起场地发生非线性响应,造成这一现象的原因是海底地质条件不均匀。作为地震动的重要特征,海陆地震动的加速度反应谱(acceleration response spectra,SAs)之间差异的研究也在不断深入。Chen等[10]898发现,震中距对中等强度海域地震动的水平SAs影响显著,海域地震动归一化SAs峰值平台较陆域地震动宽,且前者的特征周期大于后者;当周期较小时,海域和陆域地震动差异不大,但在中长周期,海域地震动SAs大于陆域地震动SAs。
由于海底沉积物及场地条件的影响,长周期成分丰富是海域地震动一个显著的特点[6]133。研究表明,海域地震动长周期反应谱大于陆域地震动[12-15]。海底沉积层厚度、地下结构、海底地形及水层等因素可能放大海底地震动的长周期分量[6]141,导致海底长周期地震动振幅远大于陆地场地[4]8。因此,海域长周期地震动应当被格外关注。
建立海域地震动预测方程(ground motion prediction equations,GMPEs)可以海域概率地震危险性分析[16-17]和海域区划提供参考。随着海洋资源的开发和近海工程的建设,海洋工程和近海重大的交通工程的抗震设防在其建设过程中是至关重要的。而在海洋工程和近海重大交通工程的抗震设防过程中,输入地震动的选取是重要一环。相比于传统地震动记录选取方式,基于广义强度指标的地震动记录选取综合考虑了多种强度指标的影响[18-19]。海域地震动预测模型的建立是基于广义强度指标的地震动记录选取的重要基础。俯冲带是一个板块斜插到相邻板块下并与之结合而成的区域,因俯冲带特殊的构造,发生在俯冲带的地震与非俯冲带地区存在较大差异[20]。因此,在研究俯冲带地区的GMPEs时需考虑其特殊构造。目前,一些应用于俯冲带地区的GMPEs被开发[21-24],但现有的GMPEs大多基于陆域地震动数据[25-28]。Hu等[22]2585建立了0.05~5.0 s的海域水平向与竖向反应谱GMPEs,但目前没有反应谱预测模型将周期延长至15.0 s。
本文基于日本K-NET台网的892组三向海域地震动记录及其相同地震事件且震源距相近的4 033组三向陆域地震动数据,建立了周期0.05~15.0 s水平向和竖向海域的SAs及PGA的GMPEs,其中水平方向的反应谱值取两个水平方向的几何平均值。本模型不仅考虑了震级、震源深度、震源距等因素,而且考虑俯冲带震源类型以及海域和陆域地震动场地项的影响,并分析了其对预测值的影响。
1 地震动数据
本文收集了K-NET台网相模湾地区ETMC海底台站2000至2020年9月所有强震记录,并按照以下要求进行筛选:①矩震级(MW)范围为4.0~6.8;②震源距不大于300 km;③震源深度不大于180 km。除满足上述条件外,所选地震动记录应同时包含P波和S波的起始频率,且信噪比不小于3.0。共计892组三向海域地震动数据,来自273次地震事件。由于本文所选海域地震动数据的震源距在300 km以内,但300 km震源距范围内矩震级大于6.8的记录很少,因此本文所建立模型的适用震级范围为M≤6.8。为对比海域与陆域地震动的差异,本文收集了相邻陆地台站4 033组陆域地震动数据,来自上述273次地震事件的中263次地震。上述地震事件来自日本俯冲带地区,为研究不同震源类型对GMPEs影响,本文根据震源位置、震源深度和震源机制将俯冲带地震分为壳内地震、板间地震和板内地震[29]。
由于噪声以及仪器倾斜等因素,可能会导致地震动数据中存在噪声及基线漂移的现象。因此需要通过基线校正的方式使地震动记录回归零基线,本文基线校正采用Boorer等[30-31]提出的基线校正方法。为保证在地震动记录不失真,选用4阶Butterworth非因果滤波器对地震动记录进行滤波处理,截止频率为0.05~25.0 Hz,该滤波器通过对地震动数据进行补零的操作避免了兼容性问题[32-33]。陆域地震动的场地Vs30数值及场地分类方式参考了Hu等[34]的研究,部分陆域台站没有剪切波速(VS30)信息,根据Zhao等[23]901的提出H/V谱比法确定自然周期,以实现对其场地条件分类。表1给出了陆域台站场地分类的标准以及各类场地的陆域地震动记录数。

表1 陆域场地分类标准以及各类场地记录数
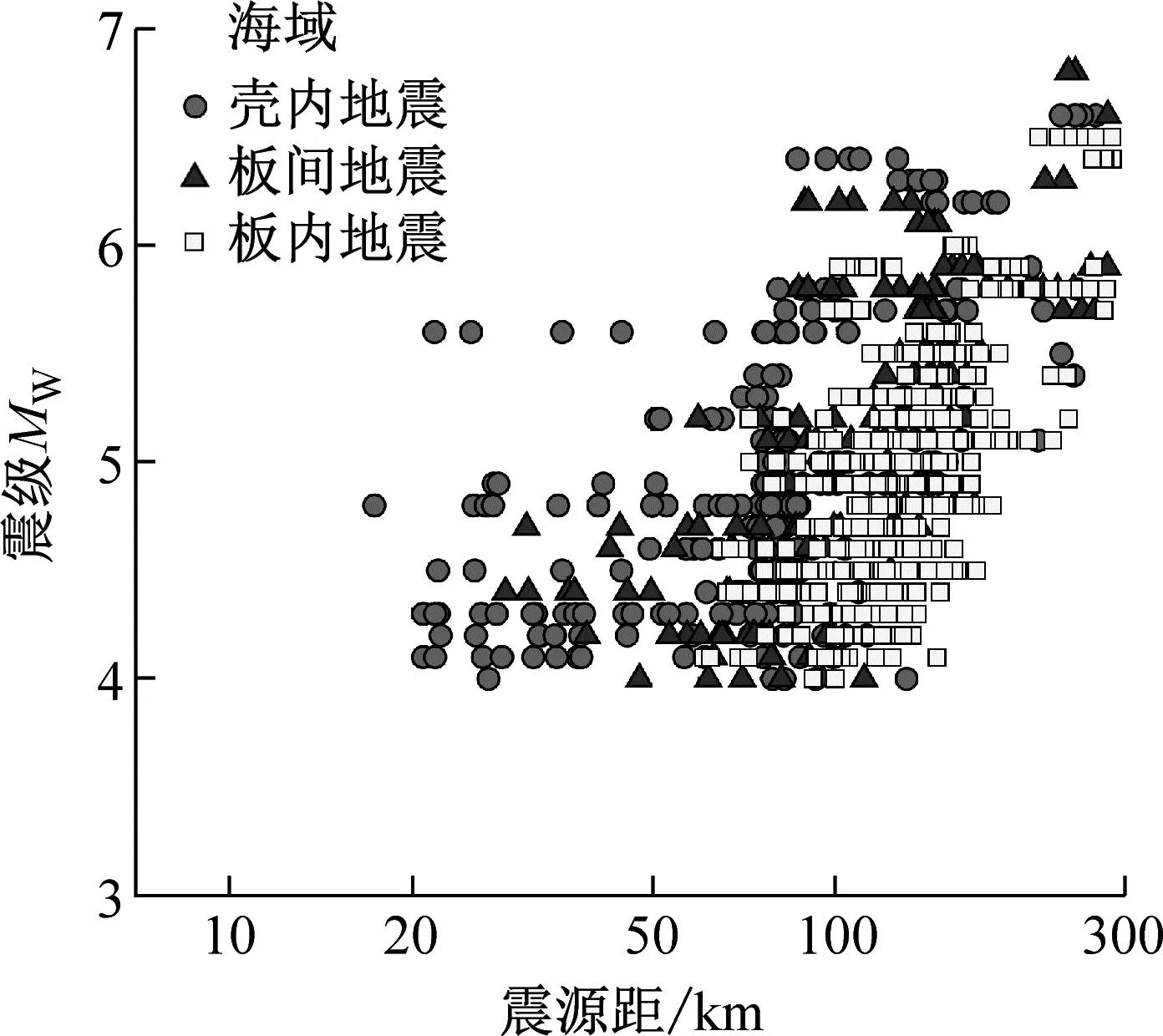
图1为本文所选海底和陆地台站以及地震震中分布。图2为本文所选地震动记录的震级与震源距分布以及震级与震源深度的散点图,对比图2(a)和(b)以及(c)和(d)可知,海域和陆域地震动的震级和震源距分布以及震级与震源深度信息等相似,符合相同地震事件且来自相邻台站的特点,可用来对比海陆地震动预测模型的差异。表2为海底台站经纬度及水深信息。

图1 海底和陆域台站以及地震震中分布
(a)

表2 海底台站经纬信息及水深
2 回归分析
由于随机效应模型具有稳定的优点[35],本文采用随机效应模型进行对0.05~15.0 s的反应谱及PGA进行回归。Hu等[22]2853通过计算6个海底台站的水平与竖向反应谱比,发现6个台站反应谱比有很大差异,说明其场地条件存在较大差异,因此本文采用单个台站作为海域场地修正项进行回归。本文所提模型综合考虑了震级、震源距、震源深度以及震源类型和场地类别,模型形式如式(1)所示
(c4-1)ln(Ri,j+c5)+c6(h-hc)δh+
c7Fi+c8Fs+Sk+SCp+ηi+ξi,j
(1)
式中:y为阻尼比为5%时的SAs或PGA;Mw为单次地震事件的矩震级;R为震源距;h为单次地震事件的震源深度。在本模型中,当h<15 km时,其值取为15 km,当h>130 km时,其值取为130 km;Fi和Fs为表征俯冲带震源类型的所构造的虚拟变量,当Fi=1,Fs=0时为板间地震,当Fi=0,Fs=1时为板内地震,Fi=0,Fs=0时为壳内地震;Sk为海域场地修正项,k=1,2,3,4,5,6,分别代表KNG201-KNG206的场地条件,SCp为陆域场地修正项,p=1,2,3,4,分别代表陆域台站的Ⅰ、Ⅱ、Ⅲ、Ⅳ四类场地。c5为考虑近场记录反应谱饱和现象所引入的一个系数,由于震源距0~10 km的近场记录较少,所以通过试错法将c5取为5;δh是震源深度有关的一个虚拟变量,当震源深度大于15 km时,其值取为1,hc为一个深度项常数,在本模型中取15 km。i表示第i次地震事件,j第i次地震事件中的第j条记录。ηi是一个随机变量,表示第i事件的事件间残差,其均值为0标准差为τ,ξi,j是表征事件内残差的随机变量,其均值为0,标准差为σ。式(1)模型中的系数c1~c8中,除c5是固定值外,其余均系数通过回归分析的方式获得。表征海域场地的系数Sk以及表征陆域场地的系数SCp同样通过回归分析的方法获得。
模型的总的不确定性分为事件间的不确定性和事件内不确定性,事件间的不确定性和事件内的不确定性通常只与模型的谱周期有关,在认为总残差均值为0的情况下,其标准差σT的计算公式如式(2)所示
(2)
式中,σ和τ分别为事件内和事件间残差的标准差。
式(1)的模型水平向和竖向地震动记录的回归结果如表3~4所示。
3 回归结果分析
3.1 残差分析
为检验本文建立的GMPEs的合理性,通过残差分析验证。本文分别计算了PGA和给定周期(T=0.2 s、T=1.0 s、T=5.0 s、T=8.0 s、T=12.0 s)的残差。图3~5分别给出了水平向GMPEs事件内残差与震源距,事件间残差与震级及震源深度的分布。根据震源距、矩震级以及震源深度将残差分为6组,图中正方形表示每组残差的均值,线条表示每组残差的+/-1倍标准差。由图3~5可知,残差的均值整体上接近0,可以认为本文所建立的模型所计算的残差值与震源距、矩震级以及震源深度的分布整体上是无偏的,因此本文所提模型的事件内及事件间残差的分布是合理的。说明本模型是鲁棒的、适合的。可以应用在日本相模湾地区长周期海域地震动反应谱的预测。
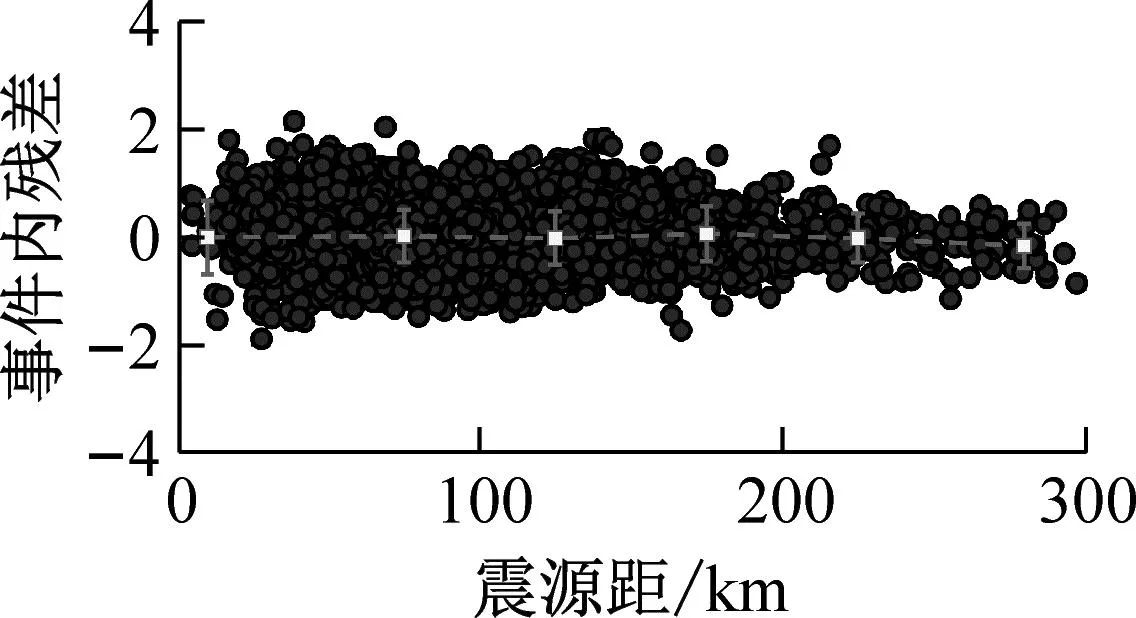
(a) PGA
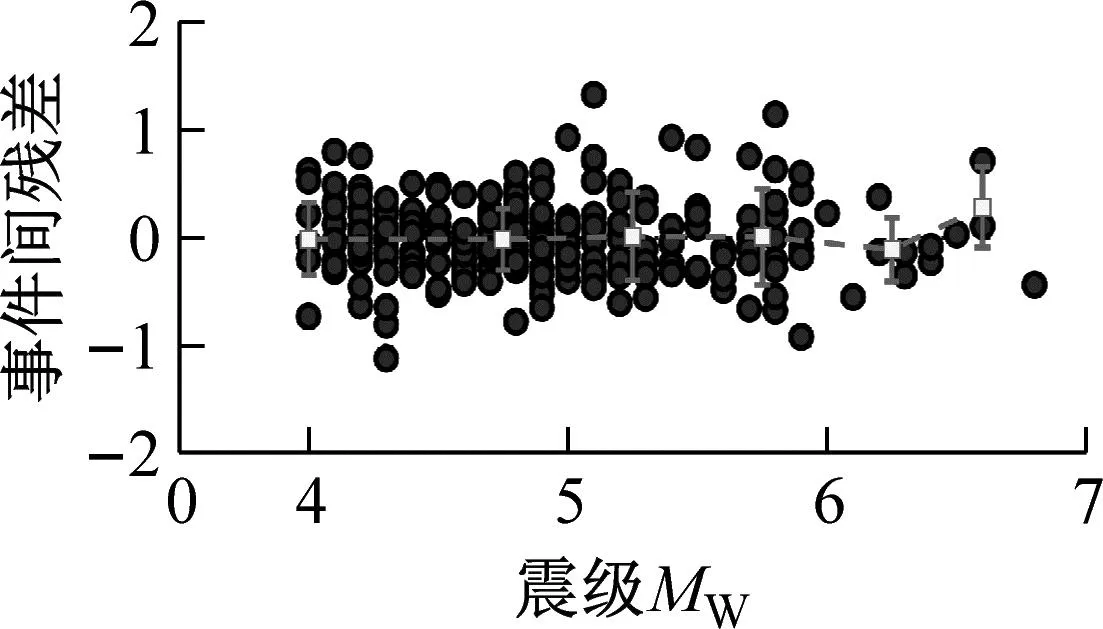
(a) PGA
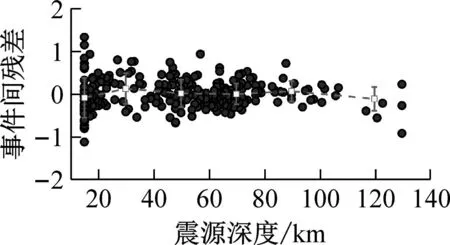
(a) PGA
图6给出了水平向和竖向模型的事件间、事件内和总残差的标准差随谱周期的变化情况,水平向总残差的标准差值在0.58~0.70,当T=0.2 s,其值达到最大。竖向总残差的标准差值在0.53~0.70变化,同样当T=0.2 s,其值达到最大。水平向与竖向的事件内残差的标准差大于事件间残差的标准差。这一结果与现存的俯冲带地区的加速度反应谱预测模型接近,Hu等[22]2588建立的海域地震动水平向反应谱预测模型(以下简称Hu2020)所计算的总残差的标准差的范围在0.59~0.72,Hu2020竖向模型的总参差的标准差的范围在0.54~0.70,本文所建立的模型所计算的总参差的标准差与Hu2020较为接近,且略小于Hu2020所计算的总查查的标准差,说明本文所建立的模型在预测相模湾地区的海域地震动反应谱方面的离散性略低于Hu2020,这也再次证明了本文所建立模型的鲁棒性。
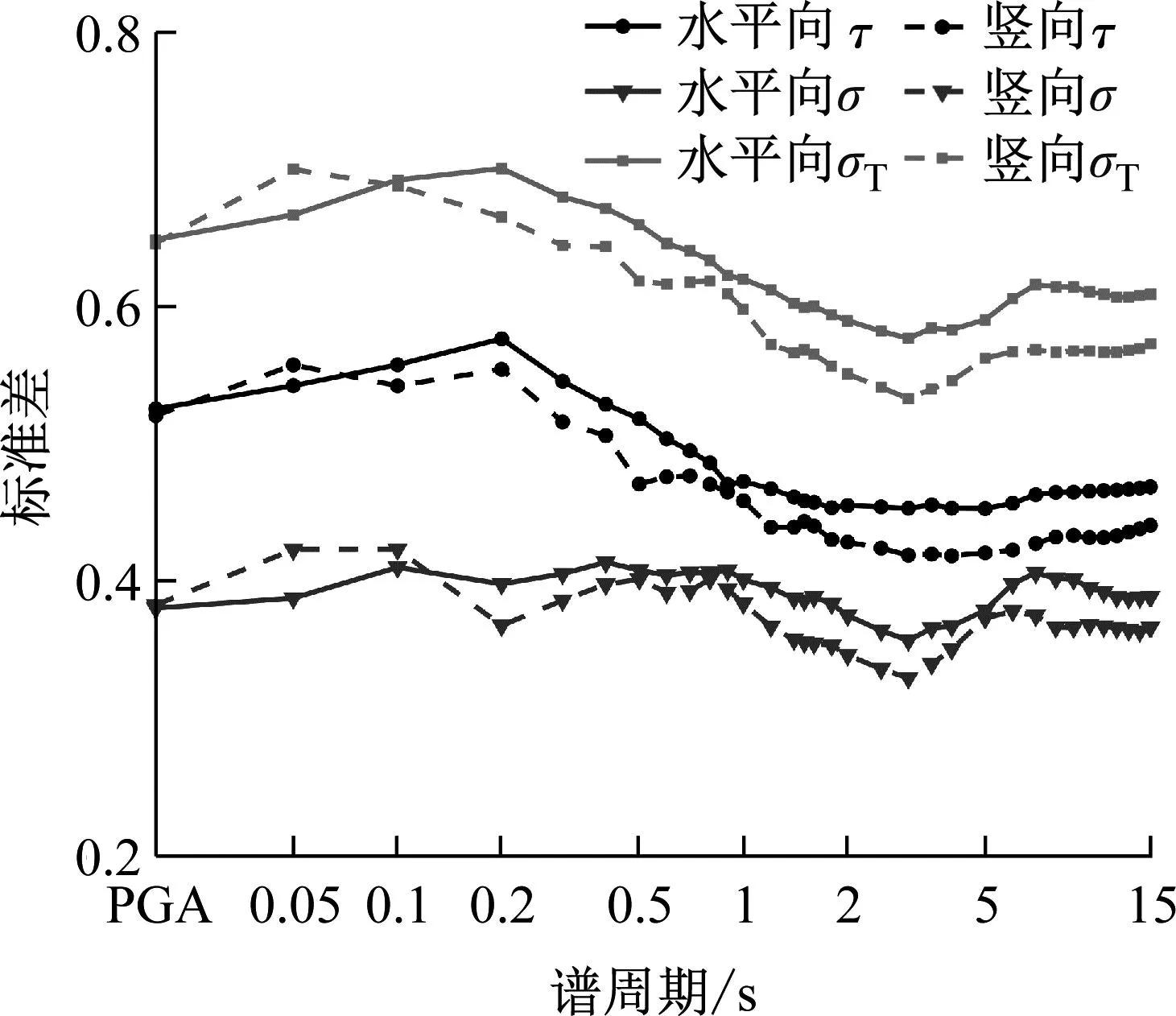
图6 所提预测模型在不同谱周期下的事件间、事件内和总参差的标准差的变化
3.2 相关性分析
图7显示了水平向GMPEs在PGA和给定周期下反应谱的预测结果与由实际地震动计算的SAs的相关性。图中实线表示取对数的实际值与预测值相等,虚线表示实际值+/-1倍标准差。并给出了本文所建立模型所计算PGA和给定周期的反应谱的总残差的标准差,在3.1节通过分析总残差的标准差并与现有模型对比,证明的总残差的标准差的合理性。分析图7可知,多数散点均处于两条虚线之间,说明在误差允许的范围内预测值与观测值有较好的相关性。因此,本文所提模型能够较好地预测日本相模湾地区海域长周期地震动反应谱。
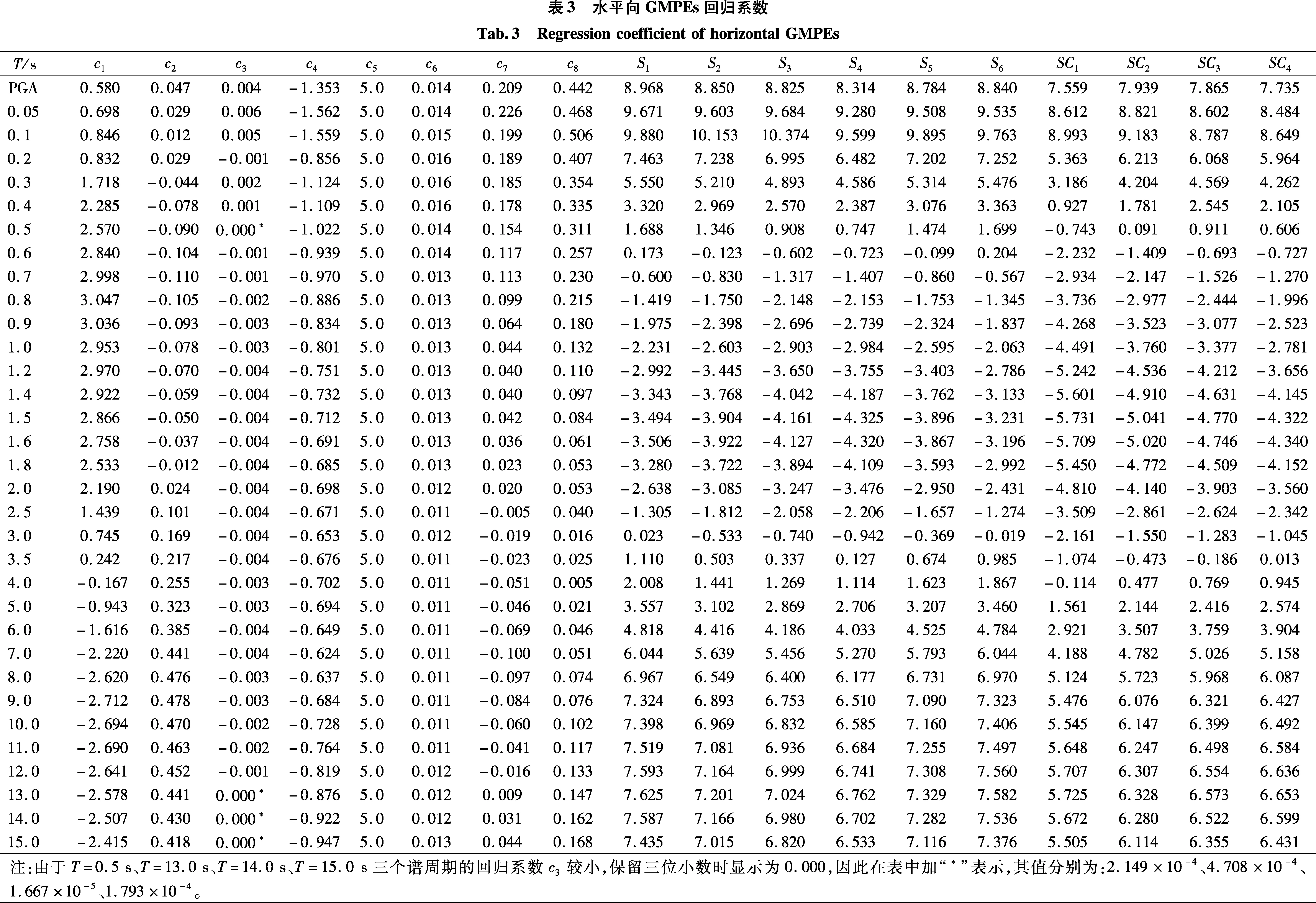
(a) PGA
3.3 深度因子及震源类型分析
当h=15 km,Fi和Fs都为0时为方程(1)模型的基础模型,适用于震源深度不大于15 km的壳内地震,基础模型的形式参考了Zhao等[23]90的研究,其通过基础模型与考虑震源深度的模型分析了震源深度对预测值的影响,结合本文建立的预测模型,本文给出的基础模型形式为
c5)+c6(h-15)+Sk+SCp+ηi+ξi,j
(3)
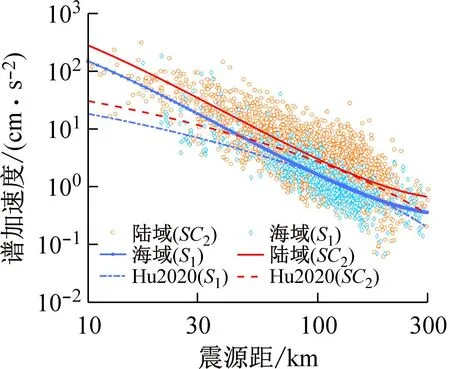
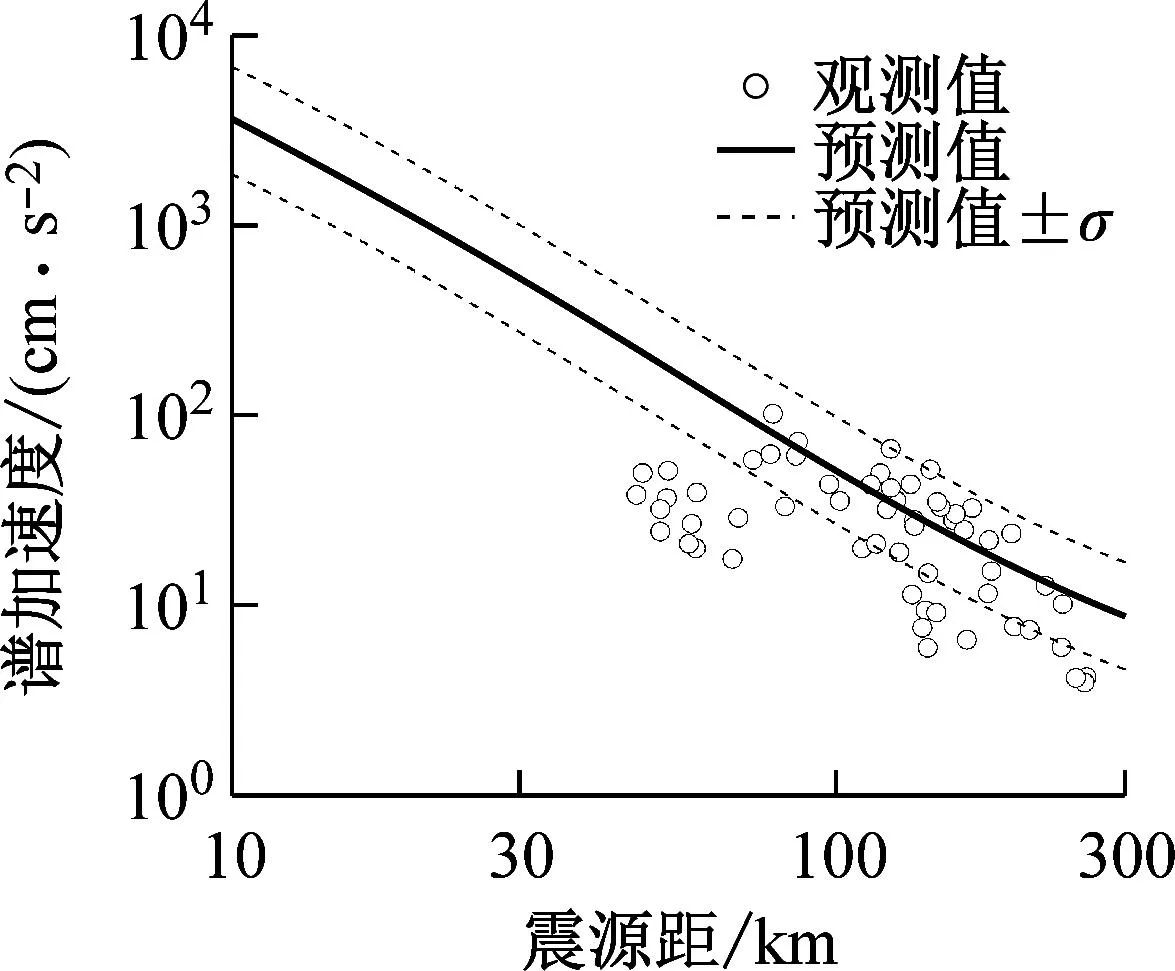
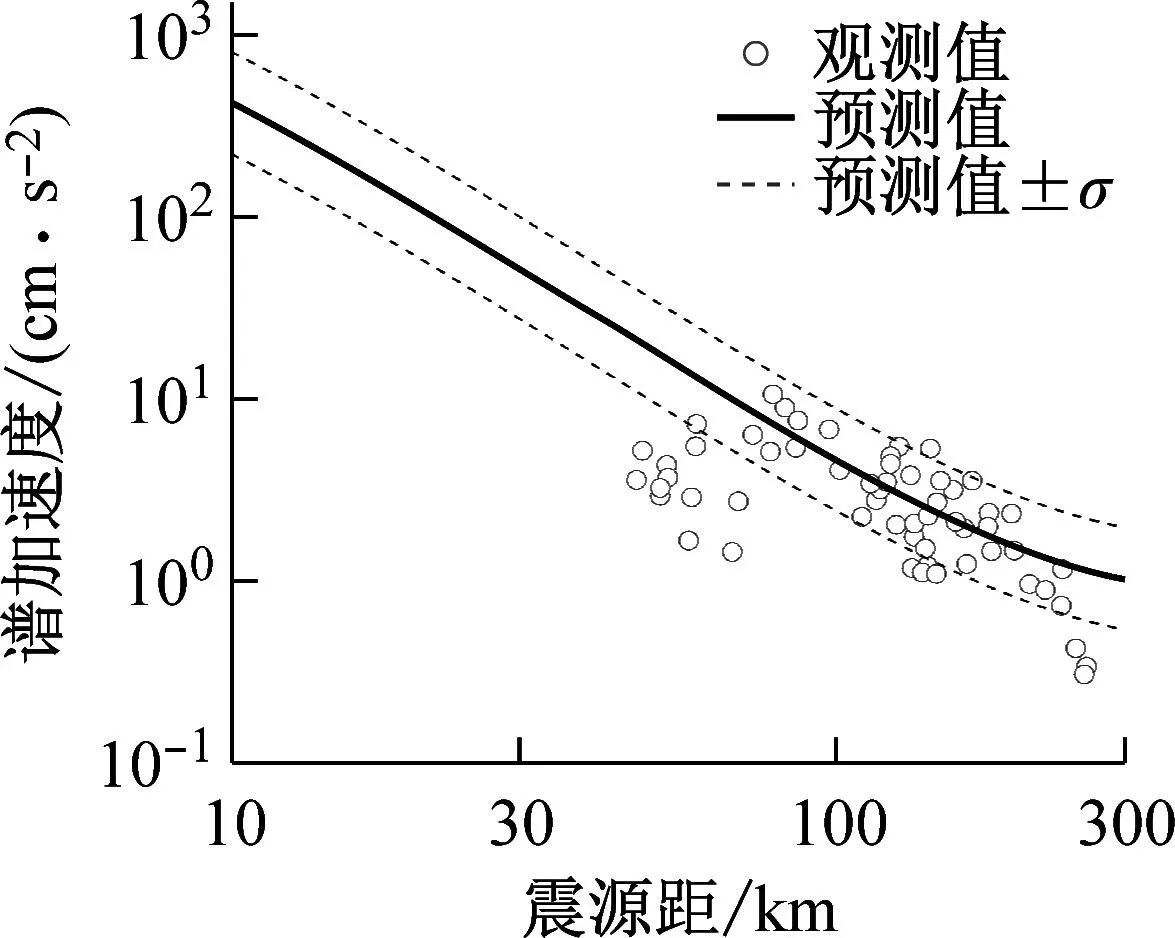
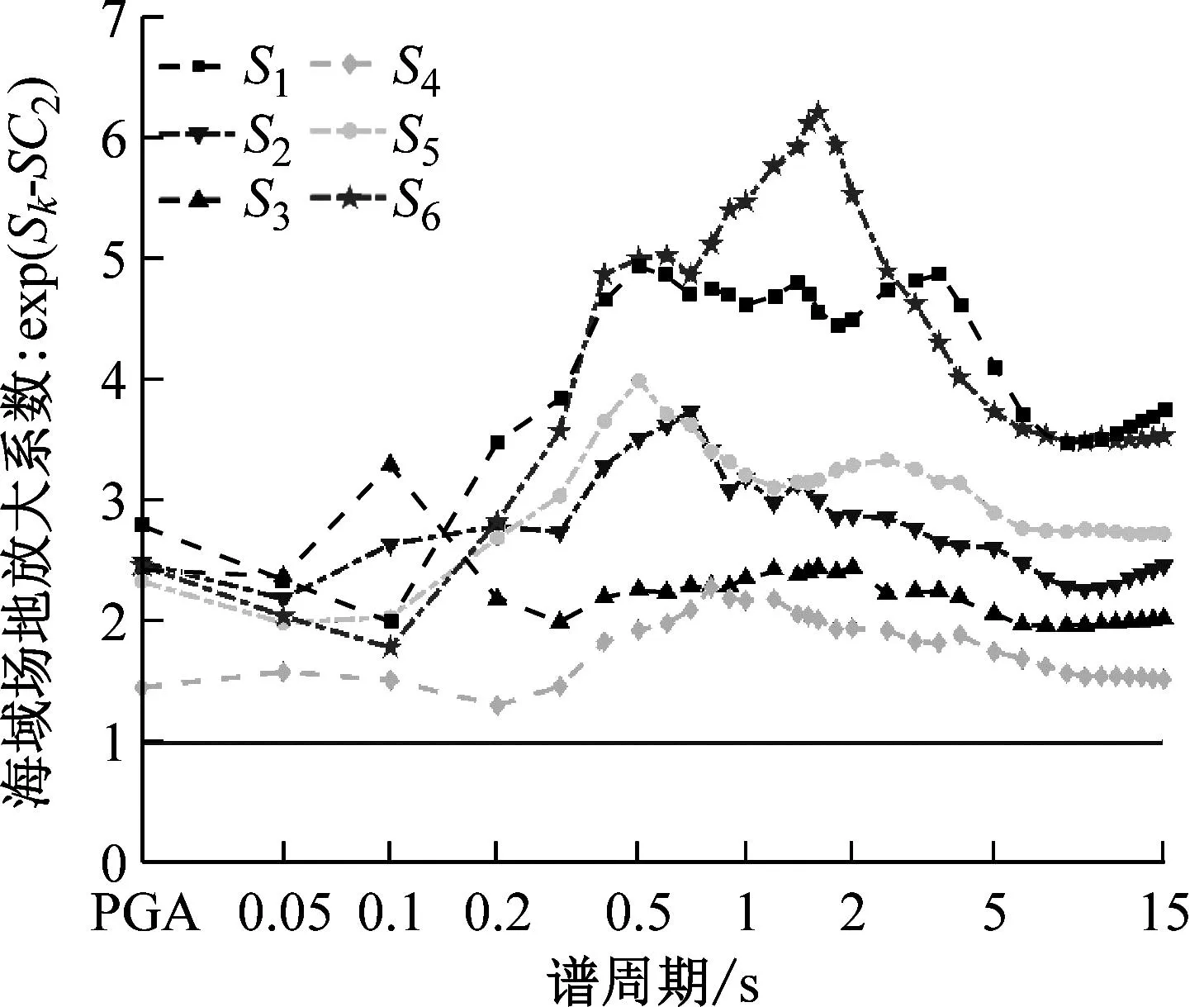
通过式(3)计算的基础模型预测值,即不考虑震源深度和震源类型。基础模型预测值加上震源深度项,得到不同的预测值,其与基础模型预测值的比值即为“深度因子”。图8(a)、(b)分别给出了水平向和竖向海域GMPEs深度比例因子在随周期的变化,其可显示震源深度对预测SAs以及PGA的影响。观察图8可知,水平向和竖向模型的震源深度的影响随周期变化的趋势不同,水平向模型的深度比例因子在当0.05 s (a) 水平向 通过式(3)计算的基础模型预测值,即不考虑震源深度和震源类型。基础模型预测值加上震源类型项,得到不同的预测值,其与基础模型预测值的比值即为“震源类型因子”。图9给出了所提水平向和竖向海域GMPEs的震源类型比例因子在不同周期下的变化,其可显示震源类型对预测SAs的影响。观察图9,当0.05 s 图9 本文所提模型的震源类型因子 图10~11分别给出了水平向和竖向模型在给定震级、给定震源深度以及给定震源距情况下的预测反应谱,海陆模型分别以S1以及SC2单场地项为例说明。由图10可知在全周期段,水平向海域模型预测的SAs大于陆域模型的预测的SAs。由图11可知,在中短周期范围内,竖向海域模型预测的SAs的值小于陆域模型预测的SAs的值,但在长周期范围内,竖向海域模型预测的SAs的值大于陆域模型预测的SAs的值。这一结论与Hu等[22]2591研究结果一致。 (a) R=50 km (a) R=50 km 图12~13为归一化为MW5.0的PGA和给定周期下的SAs与震源距的分布情况,分别给出了海域场地条件S1以及陆域场地条件SC2分布情况并给出了对应条件下的GMPEs中值,其震源深度为40 km,震源类型为壳内地震,归一化方法参考了Kanno等[36]提出的方法。与此同时,对比了现有海域GMPEs[22]2577。由于Hu2020的适用范围为0.05~5.0 s,因此T大于5.0 s的GMPEs给出预测模型中值同时本文给出了其均值±1倍的总参差的标准差的趋势线,即图12~13中的虚线和点划线。由于小于10 km的近场记录很少,因此本文所提GMPEs可靠的震源距范围为15~300 km。 (a) PGA 如图12所示,本文所提水平向预测模型的预测值与日本相模湾地区海域地震动及其相邻台站的陆域地震动反应谱的实测值可以较好地吻合,因此本文所提海域地震动预测模型较好地捕捉了日本相模湾海域地震动反应谱的衰减特征。海域水平向模型所预测结果在全周期段都大于陆域模型所预测结果。如图13所示,本文所提竖向预测模型同样可以较好地与实测记录的反应谱较好地吻合,因此本文所提竖向模型也较好地捕捉到了日本相模湾海域地震动竖向反应谱的衰减特征。海域竖向模型所预测结果在中短周期范围内小于陆域模型所预测结果,但在长周期范围内大于陆域模型所预测结果。所提水平向和竖向模型的预测结果在震源距为15~300 km的范围内与Hu2020结果较为接近,说明了本文所提水平向模型的可靠性。 (a) PGA 为进一步验证本文所提模型的合理性,本文搜集了日本相模湾海域的未参与回归的海域地震动数据。时间范围为2020年10月—2023年5月,MW均大于5.0,且同一次地震至少被三个海底台站记录,共计58组三向海域地震动记录。本文将58组地震动记录的地震情景归一化为预设的地震情景,即MW为6.0,震源类型为壳内地震,震源深度为40 km。图14~15给出了上述58组海域地震动水平向和竖向在给定地震情景下的反应谱的衰减趋势以及预测方程的均值和均值+/-1倍标准差。实线表示预测方程的均值,虚线表示均值+/-1倍标准差。由图14~15可知,未参与回归的海域地震动水平向和竖向反应谱的值与本文所建立的预测方程的拟合效果虽然没有参与回归的记录的反应谱与预测方程的拟合效果好,但多数点位于均值+/-1倍标准差的曲线中间,因此本文所建立的预测方程也较好地捕捉到了未参与海域地震而动记录反应谱的衰减规律,因此可以认为本文所建立的模型可以较好地预测日本相模湾地区海域地震动反应谱。 (a) PGA (a) PGA 为进一步分析海陆模型预测SAs存在差异的原因,本文给出了水平向和竖向的海域场地放大系数,其计算方法为:exp(Sk-SC2)。由图16(a)可知,在全周期段,水平向海域模型海域场地放大系数的值均大于1。由图16(b)可知,当T较小时,竖向海域模型海域场地放大系数的值在短周期内大于1,当T较大时,竖向海域模型海域场地放大系数的值在短周期内小于1,这一现象与图10~11所显示结果一致。初步分析,可能是由于海域以及海底沉积物等作用引起,使竖向短周期的SAs迅速衰减。 (a) 水平向 本文基于日本K-NET台网的海域地震动数据,综合考虑震级、震源距、震源深度以及震源类型和场地条件,提出了日本相模湾地区海域长周期GMPEs,并给出了该地区相近台站的陆域GMPEs。该模型能够较好地预测该地区自振周期0.05~15.0 s的SAs。分析了震源类型以及震源深度等因素对预测模型的影响,对比了海陆预测模型的差异。主要结论如下: (1) 通过震源类型因子和震源深度比例因子,分析二者对预测模型的影响,发现震源类型和震源深度对模型预测的结果影响显著。 (2) 水平向海域模型的SAs大于陆域模型SAs。在中短周期范围内时,竖向海域模型预测的SAs小于陆域模型所预测的SAs,但长周期时,竖向海域模型预测的SAs大于陆域模型所预测的SAs。 (3) 水平向的海域场地放大系数以及竖向海域场地放大系数在长周期段大于1。初步分析可能是海水深度以及海底沉积层厚度的影响。 在本模型中,近场地震动反应谱的预测结果不如中远场可靠,其主要原因是近场海域地震动数据的缺少,未来随着海域地震动数据的逐渐丰富,可进一步探讨近场预测模型的修正。由于数据的局限性,本文所提模型仅适用于相模湾地区,是否适合其他地区尚需进一步验证。 致谢: 感谢日本K-NET台网(https://www.kyoshin.bosai.go.jp/)为本文提供的数据支持,感谢F-net为本文提供的矩震级及断层类型信息,感谢赵一男博士提供的绘图方面的帮助。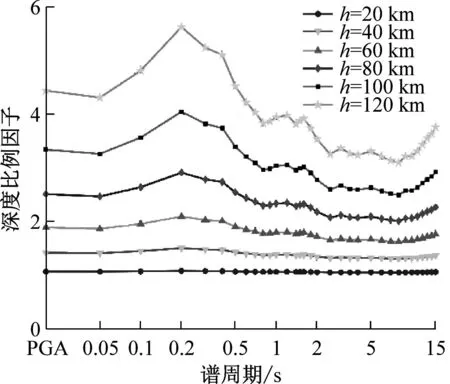
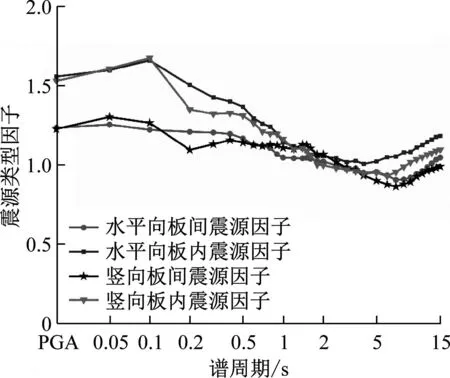
4 海陆模型预测结果对比
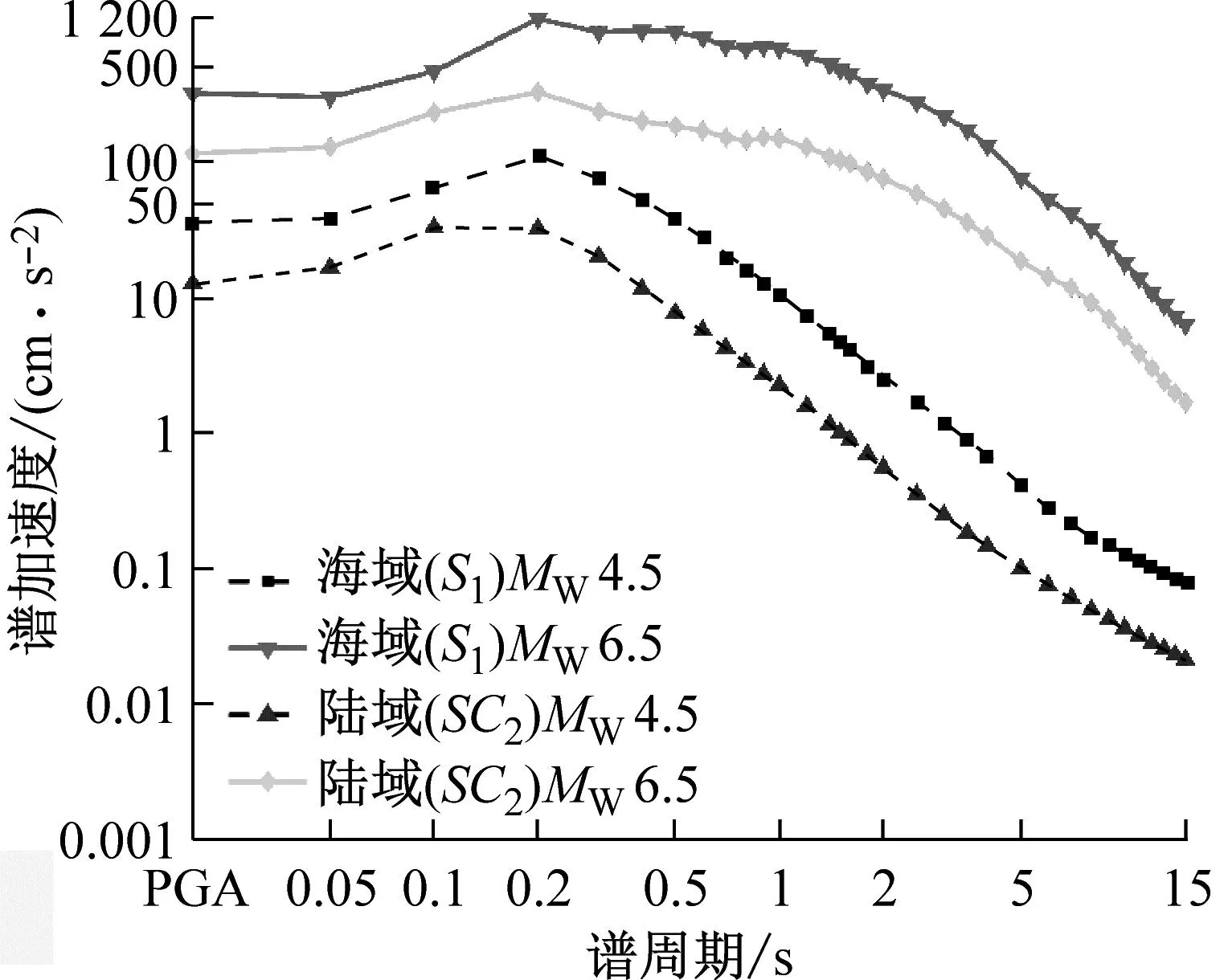
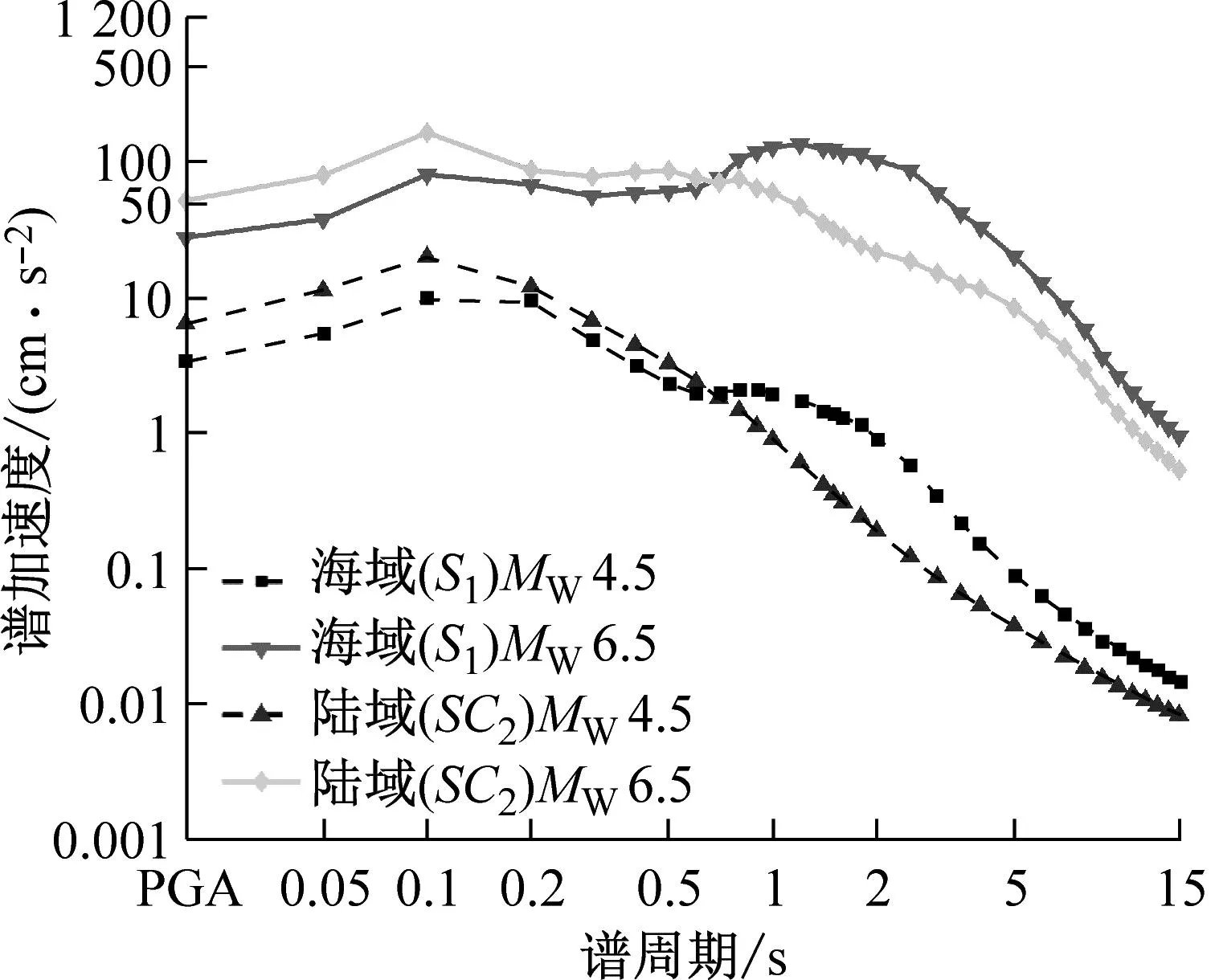
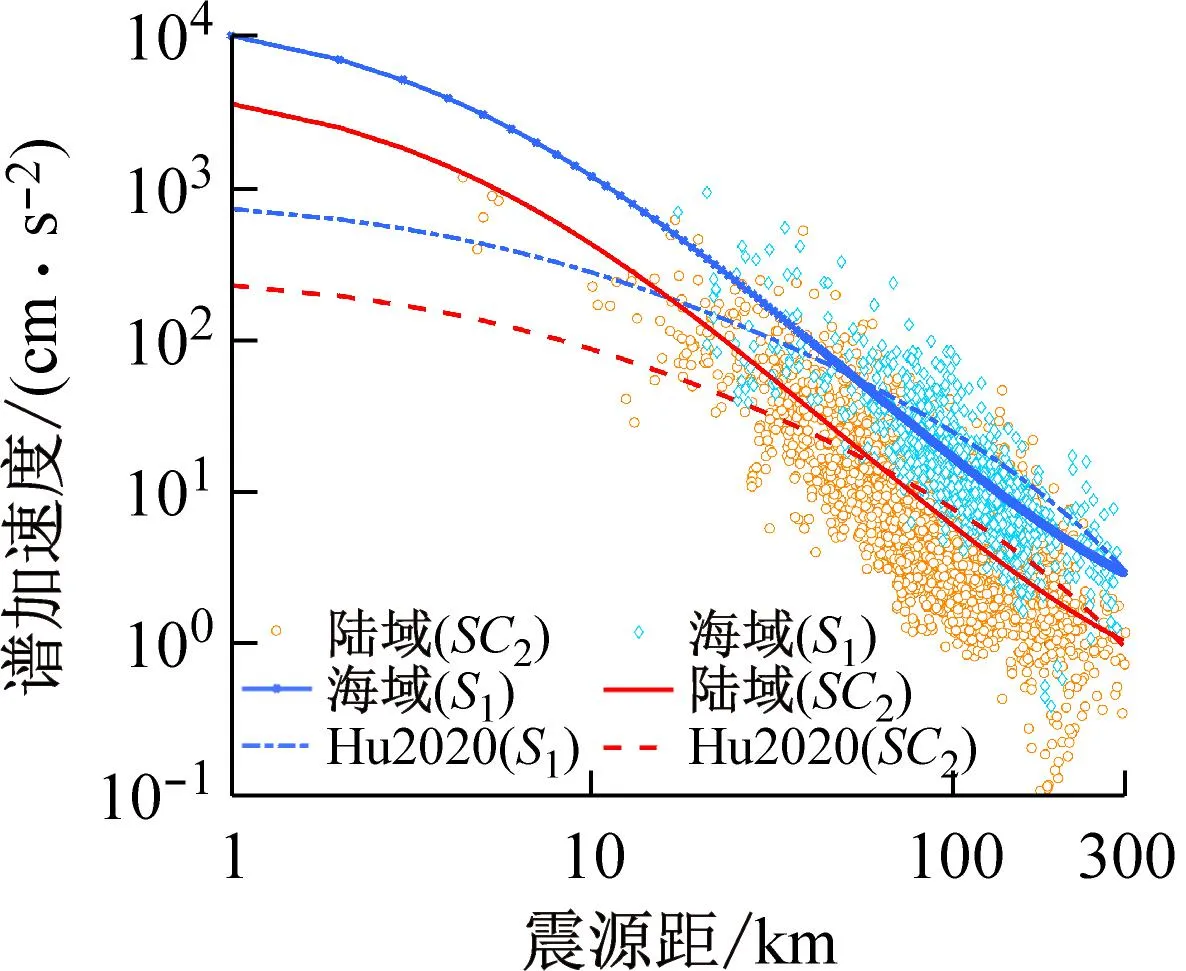
5 结 论

