圆弧形蜂窝夹芯板在低速冲击下的动力响应研究
余 阳,付 涛
(昆明理工大学 机电工程学院,昆明 650500)
蜂窝夹芯板具有质量轻、强度高、刚度大、能量吸收及减振等良好的性能,广泛应用于航空航天和船舶等冲击防护领域。根据结构的功能、使用寿命、可用性和成本的不同,蜂窝夹芯板的结构设计可以千变万化。凭借这些优势,蜂窝夹芯板受到研究者的青睐。在工程应用领域,蜂窝夹芯板容易受到鸟类或石子等物体的撞击,给蜂窝夹芯板造成损伤,导致蜂窝夹芯板的刚度、稳定性和承载能力降低,进而影响结构的安全性[1-2]。因此,能够准确地预测低速冲击下蜂窝夹芯板动力响应的模型是必要的。在低速冲击响应研究中,理论模型从弹道冲击响应到空气爆炸、水下爆炸冲击响应,使用现有的理论和数值模型进行蜂窝夹芯板低速冲击分析的理论推导,采用质量-弹簧单元、能量平衡原理和哈密尔顿原理等理论对模型进行求解,随着理论的不断丰富,蜂窝夹芯板的低速冲击模型越来越精确[3-4]。
在过去几十年里,有限元分析方法已经发展成为一种强大的技术,能够模拟各种几何形状和不同冲击载荷条件下的冲击响应[5],将试验结果和有限元仿真结果进行对比分析的研究方法受到研究者的青睐。Liu等[6]利用ANSYS基于时间步长积分的有限差分算法计算了冲击位移、应力和应变随时间的变化。姚鹏等[7]采用LS-DYNA软件对夹层结构 (sandwich plate system,SPS)的冲击吸能特性进行了模拟,并通过试验数据验证有限元仿真结果的可靠性。辛亚军等[8]通过试验和有限元模型对铝蜂窝夹芯板的面外剪切行为和力学性能进行了研究。杨姝等[9]采用势能驻值原理获得集中力与局部变形关系,通过试验、有限元及理论分析相结合方法对金属面夹芯板抗冲击性能进行研究。Zhang等[10]建立了考虑微观结构的三维有限元模型,结合试验和数值方法,推导了球面压头对夹芯板低速冲击的压痕响应和能量平衡解析模型。
在低速冲击下夹芯板动力响应的数学模型研究中,Zhu等[11]基于能量法建立了数值分析模型,将分析模型结果与试验结果进行对比,验证模型的有效性。能量平衡模型能够预测冲击过程中夹芯板结构受到的最大冲击力,但是这种方法不能提供冲击力随时间变化的趋势[12-13],这是研究夹芯板结构损伤的重要信息。而利用最小势能原理[14],通过总势能的极小化,可以得到压痕载荷与横向挠度和变形长度的关系。在冲击过程中,当夹芯板的总势能达到其最小势能时,凹陷深度最大[15]。随着理论的不断丰富,Andrews等[16]考虑动力学效应,将夹芯板建模为单自由度质量-弹簧系统,并与准静态试验结果进行了比较。金其多等[17]通过结合四阶龙格库塔法拓展了两步摄动-伽辽金法,以此研究了含黏弹性夹芯的功能梯度石墨烯增强复合材料(functionally graded graphene reinforced composite,FG-GRC) 后屈曲梁在低速冲击下的动力响应特性。朱秀杰等[18]基于精确板理论提供了一种分析复合材料格栅/波纹夹芯板屈曲特性的解析模型。Shu等[19]基于Mindlin正交各向异性板理论,得到指定边界条件下波纹夹芯板在弯曲荷载作用下的 位移闭式解。Mishra等[20]利用模态求解技术,确定了冲击点处的接触力、板与冲击器的侧向位移和速度以及板内部的应力状态。运动方程适用于特殊正交各向异性层合板的小挠度弹性响应。Sun等[21]利用哈密顿原理,提出了一种研究带金属面板的蜂窝夹芯板低速冲击响应的解析建模方法,将哈密顿原理从弹性体扩展到具有塑性的面板。Malekzadeh等[22]基于改进的高阶夹层板理论,采用弹簧-质量-阻尼器-减震器(spring-mass-damper-dashpot,SMDD)和弹簧-质量-阻尼器(spring-mass-damper,SMD)两种新型三自由度系统对冲击器与面板之间的相互作用进行了建模。
王彦斌等[23]对具有负泊松比特性的圆弧形蜂窝结构进行了力学分析研究,推导出圆弧形蜂窝胞元的等效参数。通过查阅相关文献发现,对于蜂窝夹芯板在低速冲击下的动力响应理论分析模型研究较少,而且圆弧形蜂窝夹芯板在低速冲击下的动力响应还未被研究。因此为了能更好的研究圆弧形蜂窝夹芯板在低速冲击中的动力响应,本文基于哈密顿原理和一阶剪切变形理论来推导蜂窝夹芯板的运动方程,建立两自由度的质量-弹簧模型,来研究冲击器与蜂窝夹芯板之间的接触力,采用Navier法和Duhamel积分对蜂窝夹芯板的运动方程进行解析求解。将模型计算结果与ABAQUS有限元仿真计算结果进行对比分析,验证理论模型的准确性和有效性,同时讨论不同的蜂窝胞元参数对蜂窝夹芯板动力响应的影响,可供其他研究者参考。
1 蜂窝夹芯板的低速冲击理论模型
在建立圆弧形蜂窝夹芯板的低速冲击理论模型之前,本文先假设蜂窝夹芯板是由上下蒙皮层和中间夹芯层组成,其中夹芯层是由负泊松比特性的圆弧形蜂窝胞元经过线性阵列而组成。在蜂窝夹芯板的中间平面建立笛卡尔坐标系(x,y,z),沿着x、y和z轴方向分别为蜂窝夹芯板的长度、宽度和高度,蜂窝夹芯板的长度、宽度和高度分别记为Lx、Ly和h。蜂窝夹芯板受到初始速度为vs,半径为Rs的球形冲击器的冲击载荷,低速冲击下的圆弧形蜂窝夹芯板的模型如图1所示。为了更好地计算分析,假设顶部蒙皮层的高度ht和底部蒙皮层的高度hb相等,夹芯层的高度为hc。蜂窝夹芯板的圆弧形蜂窝胞元结构如图2所示。图2中:d为胞元的壁厚;Rc为胞元的半径;θ为胞元的角度。引用王彦斌等所推导的圆弧形蜂窝结构的等效参数为
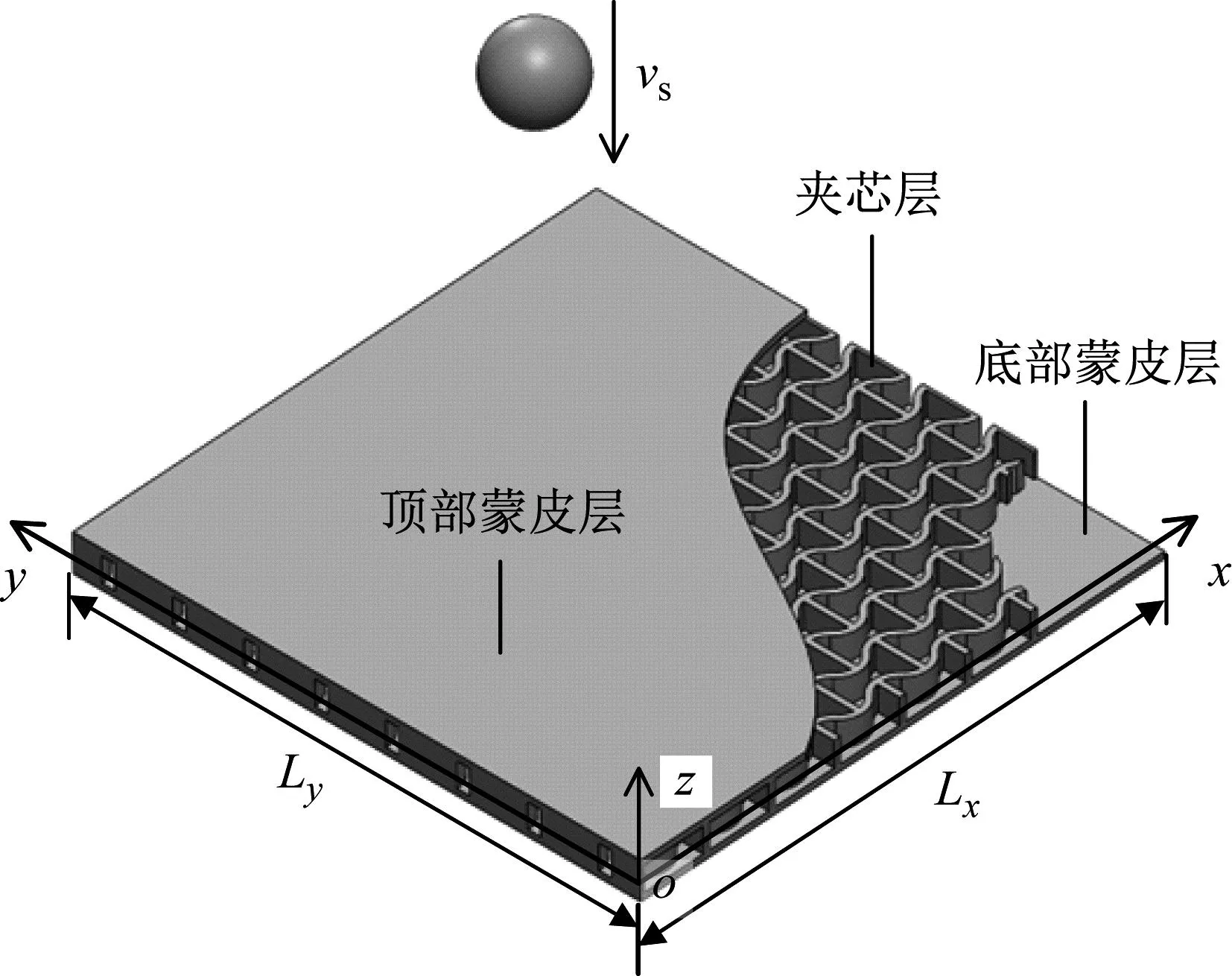
图1 低速冲击下蜂窝夹芯板模型
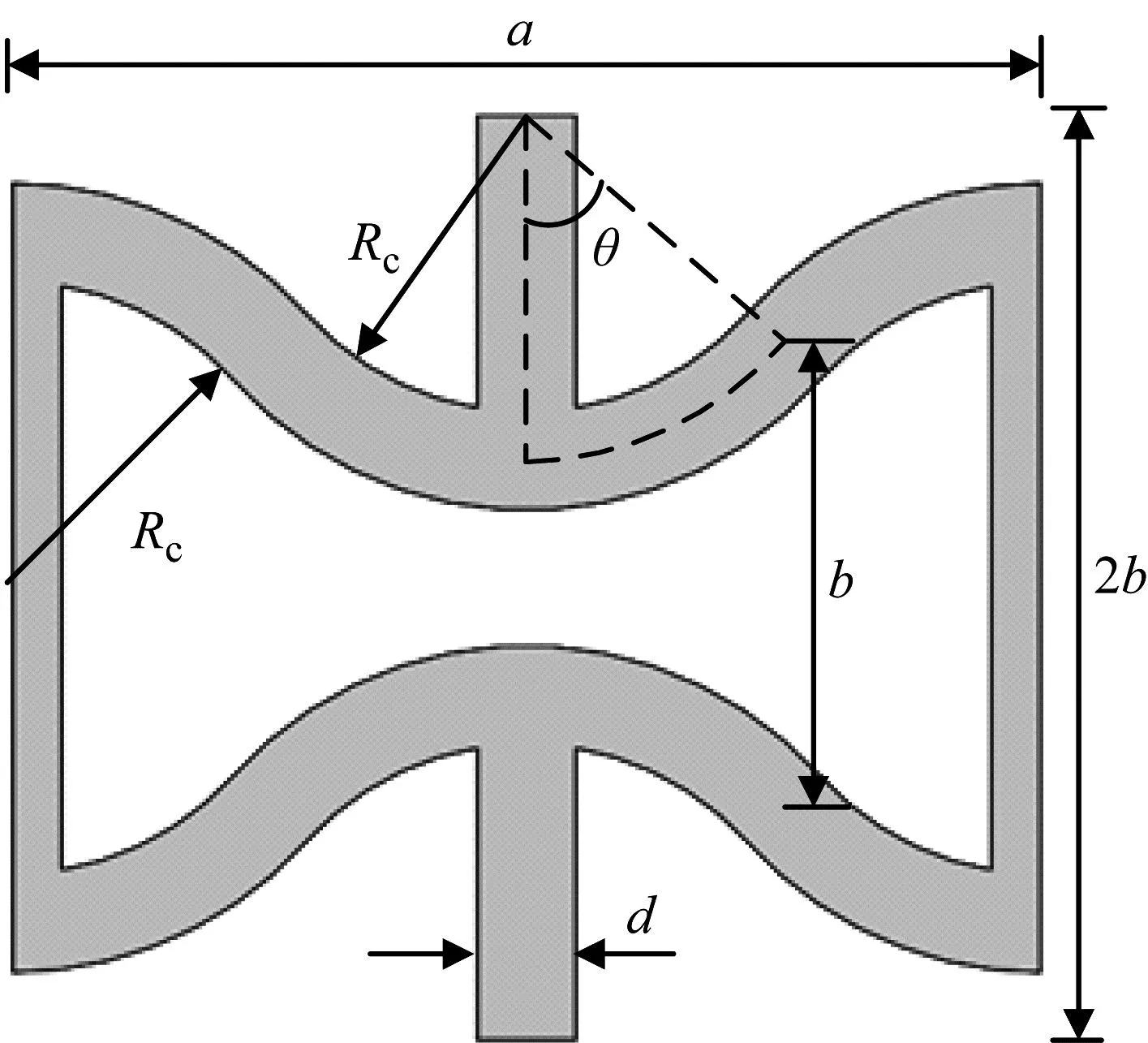
图2 蜂窝胞元结构
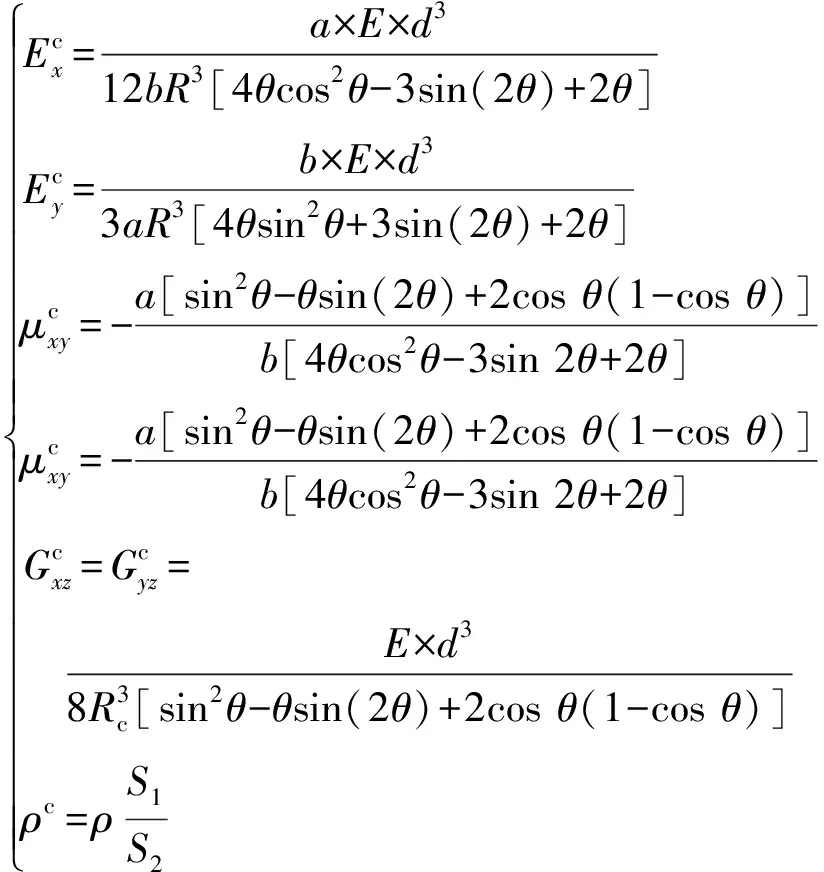
(1)
式中:a=2(2Rc+d)sinθ,b=2(2Rc+d)cosθ,S1=8π(2Rcd+d2)θ/360°+4dRc,S2=2ab;E、G和μ分别为基体材料的弹性模量、剪切模量和泊松比。
1.1 蜂窝夹芯板的运动方程
为了获得蜂窝夹芯板的位移场,采用一阶剪切变形理论,位移场方程为
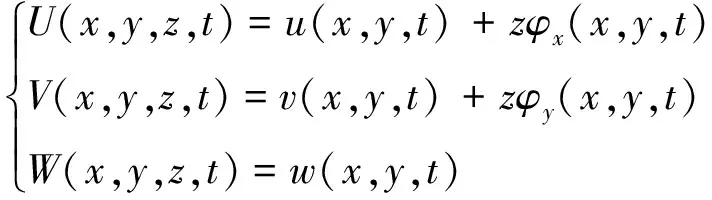
(2)
式中:u,v,w分别为中间平面相对于x轴,y轴和z轴平面内的横向位移;φx和φy为旋转位移分量;t为时间。
与位移场有关的任意位置的横向应变-位移关系为

(3)
式中:εx、εy为正应变;γxy、γxz、γyz为剪切应变。
蜂窝夹芯板的线性本构关系
(4)
(5)
(6)
式中,标量符号的上角标t、c和b分别为顶部蒙皮层、圆弧形夹芯层和底部蒙皮层所对应的参数值。
其刚度系数为
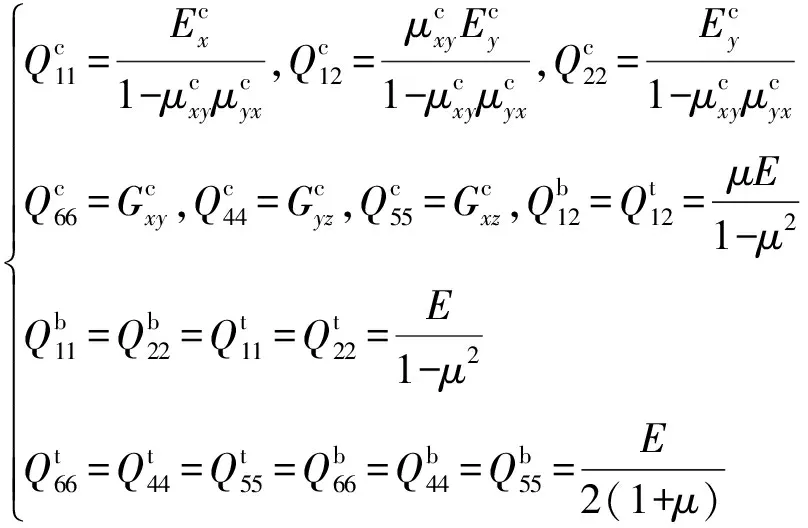
(7)
根据哈密顿原理,蜂窝夹芯板一阶剪切变形理论的运动方程为
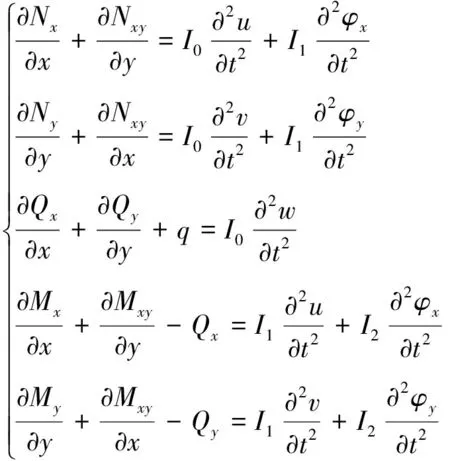
(8)
式中:q为冲击载荷;I0、I1和I2为质量惯性矩;Nx、Ny和Nxy为轴向力;Qx和Qy为剪切力;Mx、My和Mxy为力矩。
轴向力、力矩和剪切力分别为
(9)
(10)
1.2 接触力的求解方法
为了能够计算出球形冲击器与蜂窝夹芯板之间的接触力,两自由度质量-弹簧模型如图3所示。球形冲击器的质量为m1,蜂窝夹芯板的质量为m2,F(t)为球形冲击器在冲击下的接触力,δ(t)为接触后蜂窝夹芯板的接触位移。接触位移由冲击器和蜂窝夹芯板之间的位移差确定,如图4所示。
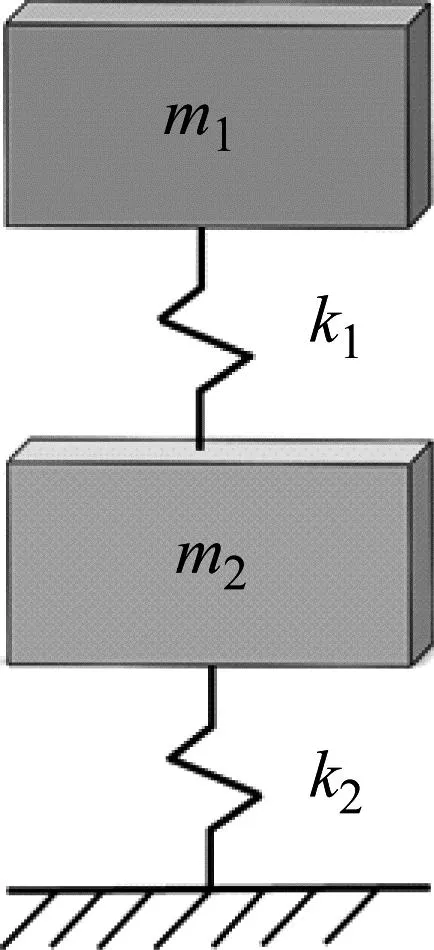
图3 两自由度弹簧质量模型
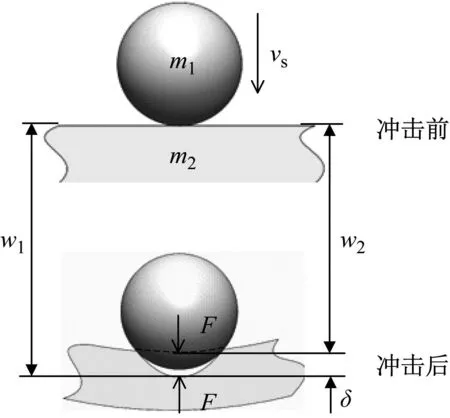
图4 球形冲击器冲击下的接触力和接触位移示意图
接触位移δ(t)为
δ(t)=w1(t)-w2(t)
(11)
式中,w1(t)和w2(t)为两个质量块在撞击后时间的位移响应。
根据参考文献[24],冲击器在冲击期间的非线性赫兹冲击力可推导为
(12)
式中,λ为弹性恢复常数,取1.5。
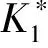
(13)
式中,Es、μs和Et、μt分别为球形冲击器和蜂窝夹芯板顶部蒙皮层的杨氏模量和泊松比。
使用等效刚度K1解析求解,接触力为
F(t)=δ(t)K1
(14)
引用参考文献[25]等效接触刚度为
(15)
式中,Γ(·)为Gamma函数。
δm最大接触变形为
(16)
应用牛顿第二运动定律,两自由度质量-弹簧系统的平衡方程为
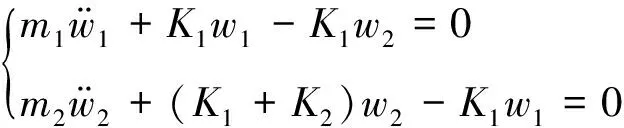
(17)
平衡方程的初始条件为
(18)
由式(11)、(14)、(17)和(18)可以推导出球形冲击器与蜂窝夹芯板之间的接触力为
(19)
其中
1.3 横向位移的求解方法
本文将蜂窝夹芯板视为四边简支边的矩形板,在这种情况下,其边界条件为
v=w=φy=Nx=Mx=0 当x=0或x=Lx
(20)
u=w=φx=Ny=My=0 当y=0或y=Ly
(21)
四边简支夹芯板的求解可以通过Navier法获得,将位移假定为如下双三角级数
(22)
式中:α=mπ/Lx,β=nπ/Ly;Umn(t)、Vmn(t)、Wmn(t)、Xmn(t)和Ymn(t)为位移振幅分量;m和n为模数。
冲击载荷q可表示为
(23)
其中,系数Qmn(t)为
(24)
将式(22)、(23)代入式(8)中,并应用Galerkin方法,忽略平面内和旋转惯性,可推导为
(25)
根据式(25),可得到一个线性二阶微分方程为
(26)
式中,ωmn为蜂窝夹芯板的固有频率。
使用Duhamel积分,将式(24)代入式(26),可推导出Wmn(t)为

(27)
使用式(19)、(22)和(27),可以得到蜂窝夹芯板的横向位移方程
(28)
式中,e1和e2为代替系数。
1.4 理论模型验证
在本节中,将理论模型计算结果与ABAQUS有限元仿真结果或已发表文献的结果进行对比分析,来验证当前理论模型可靠性和有效性。首先将理论模型与有限元仿真模型所计算的蜂窝夹芯板中心最大横向位移结果进行对比验证,蜂窝夹芯板的几何尺寸为:蜂窝夹芯板的长度与宽度分别为Lx=300 mm和Ly=300 mm,蜂窝夹芯板的总高度h=12 mm,夹芯层高度hc=10 mm,蜂窝胞元壁厚d=2 mm,蜂窝胞元角度θ=45°,蜂窝胞元半径Rc=6 mm。材料参数为:蒙皮层和芯层为相同材料,材料的弹性模量E=69 GPa,泊松比μ=0.3,密度ρ=2 700 kg/m3。球形冲击器的半径为10 mm,其弹性模量E=200 GPa,泊松比μ=0.3,密度ρ=7 871.8 kg/m3。
建立ABAQUS有限元仿真模型,首先在有限元仿真软件中对球形冲击器和圆弧形蜂窝夹芯板进行3D建模,并将材料属性赋予模型。其次对冲击器和蜂窝夹芯板两个部件进行装配,将球形冲击器参考点P与蜂窝夹芯板顶部蒙皮层中心点相接触,其接触点坐标为(Lx/2,Ly/2,h),同时将参考点P与球形冲击器进行刚体约束,在分析开始时将参考点调整到质心,然后对参考点施加速度载荷,通过改变球形冲击器的速度参数就可以达到不同速度的冲击效果。为了防止低速冲击过程中发生干预穿透问题,采用通用接触,面面接触在法向设置为硬接触,在切向设置为罚函数接触,其摩擦因数为0.2。然后创建动力显示分析步,对蜂窝夹芯板施加四边简支载荷边界条件,分别在x=0和x=Lx边,限制y方向与z方向的位移和绕y轴的旋转;在y=0和y=Ly边,限制x方向与z方向的位移和绕x轴的旋转。采用十结点二次四面体单元(C3D10)对圆弧形蜂窝夹芯板进行网格划分,其边界网格尺寸为5 mm,为了更好的分析蜂窝夹芯板横向位移,对蜂窝夹芯板的中心20 mm×20 mm区域网格尺寸设置为2.5 mm。球形冲击器同样采用十结点二次四面体单元(C3D10),其网格尺寸为1 mm。有限元软件建立的圆弧形蜂窝夹芯板低速冲击仿真模型网格划分如图5所示。
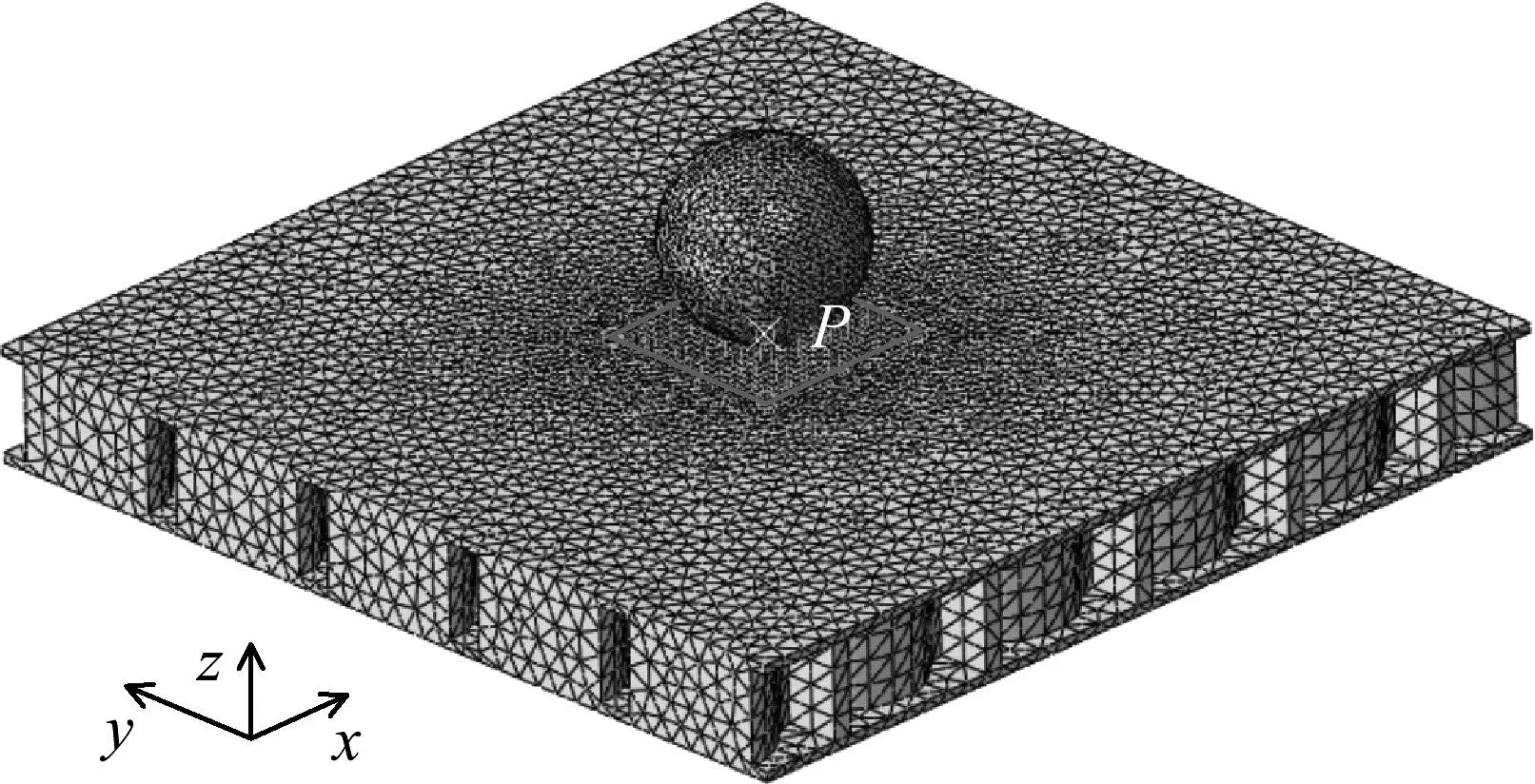
图5 有限元仿真模型网格划分
采用相对收敛性检查的方法来验证当前网格的收敛性,逐步调整中心网格尺寸,每次以近似2∶1的比例调整网格尺寸。在10 m/s的冲击速度下,中心网格尺寸分别设计为5 mm、2.5 mm、1.2 mm和0.6 mm,蜂窝夹芯板中心最大横向位移分别为0.209 mm、0.305 mm、0.307 mm和0.307 mm,有限元数值模拟计算的时间分别为90 s、90 s、141 s和360 s。使用MATLAB软件中Smoothing Spline函数对离散数据进行曲线拟合,蜂窝夹芯板的中心网格尺寸对中心最大横向位移和计算时间的影响如图6所示。由图6可知,随着网格尺寸的逐渐减小,夹芯板中心最大横向位移也逐渐趋于一个稳定值0.307 mm,其5%的误差下横向位移为0.262 mm,网格尺寸为2.5 mm时可以满足网格收敛性的要求,同时此网格尺寸下,有限元数值模拟计算出结果所花费的时间也相对较少。通过上述分析可以得出当中心网格尺寸为2.5 mm时,满足网格收敛性的要求,且有限元数值模拟计算效率较高。
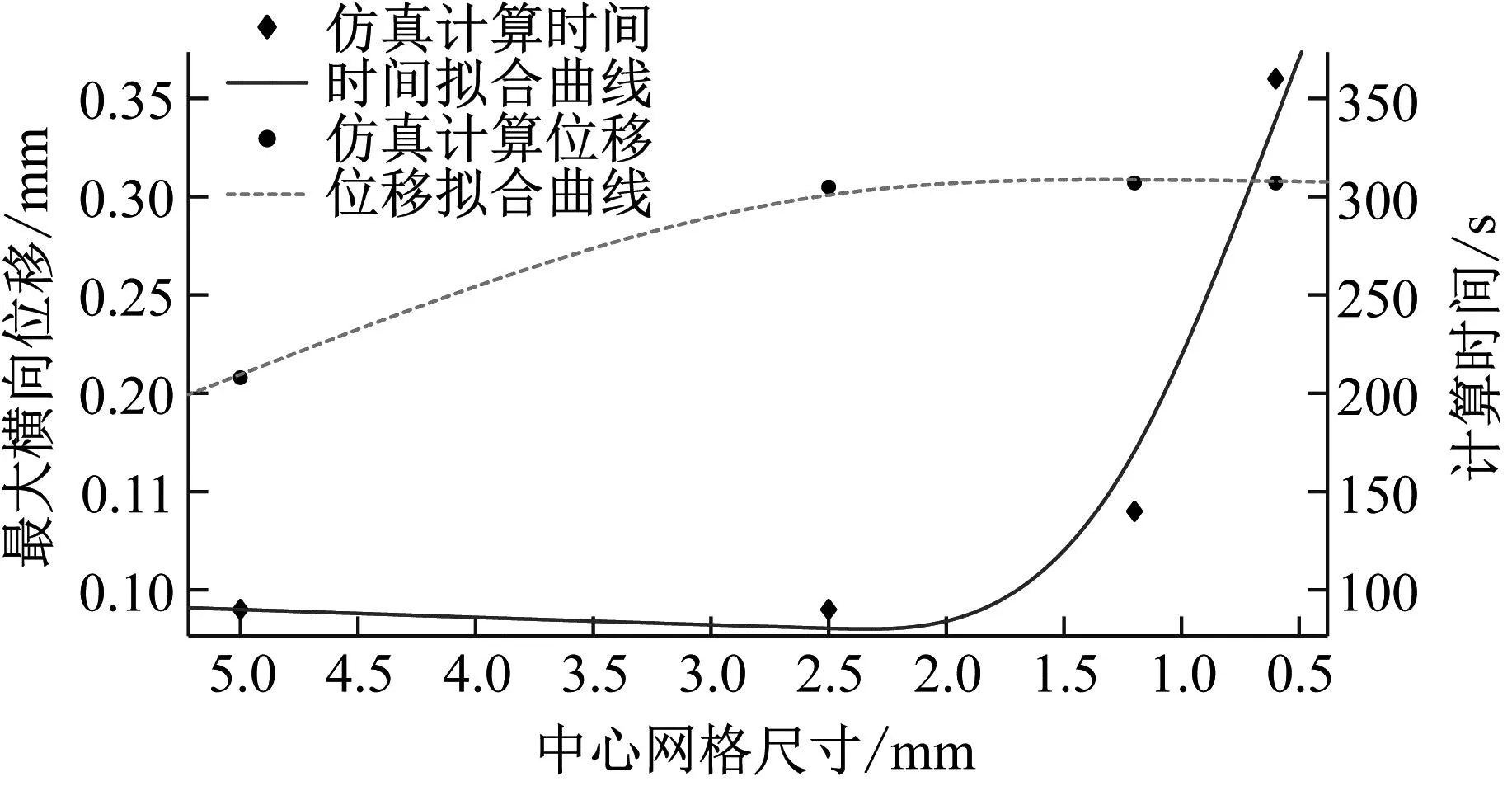
图6 中心网格尺寸对最大横向位移和计算时间的影响
在不同的冲击载荷下,采用上述有限元仿真模型与本文理论模型所计算的中心最大横向位移如表1所示。由表1可知,有限元仿真结果与本文理论模型计算结果最大的相对误差为4.9%,验证了本文方法的正确性。
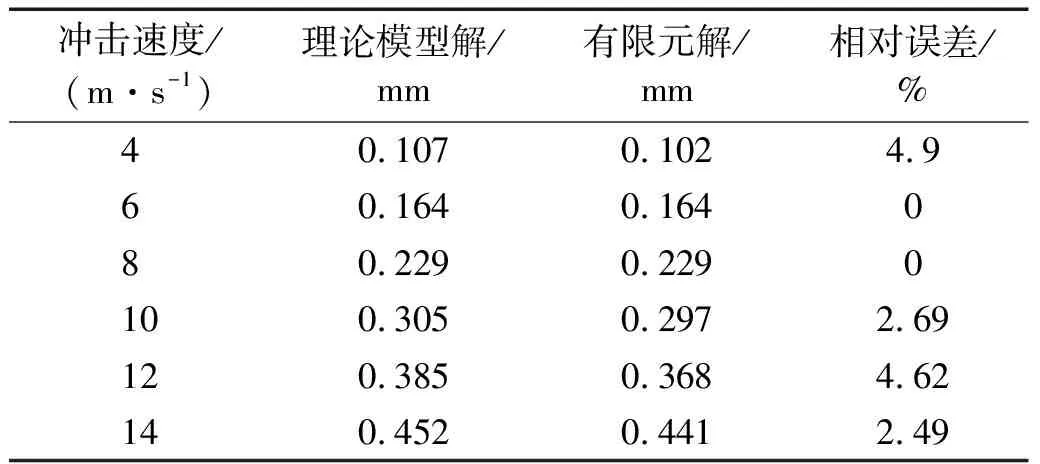
表1 圆弧形夹芯板中心最大横向位移
最后利用本文所建立的理论模型求解方法来计算球形冲击器和矩形板的接触力,并与Yang等[25]和Wu等[26]计算的接触力进行对比研究。矩形板结构的长宽高分别为200 mm、200 mm和8 mm,球形冲击器半径为10 mm,冲击器与矩形板的材料密度ρ=7 971.8 kg/m3,弹性模量E=200 GPa,泊松比μ=0.3,冲击器以1 m/s的速度冲击矩形板。本文研究预测的接触力分布与文献[25]和文献[26]得到的接触力分布对比如图7所示,从图中可以看,本文的分析模型预测的最大接触力高于文献[26]的试验结果,低于文献[25]的试验结果,矩形板与球形冲击器之间的接触力总体变化趋势相同,理论模型与参考文献的接触力最大误差为8%,验证了当前理论模型的有效性。
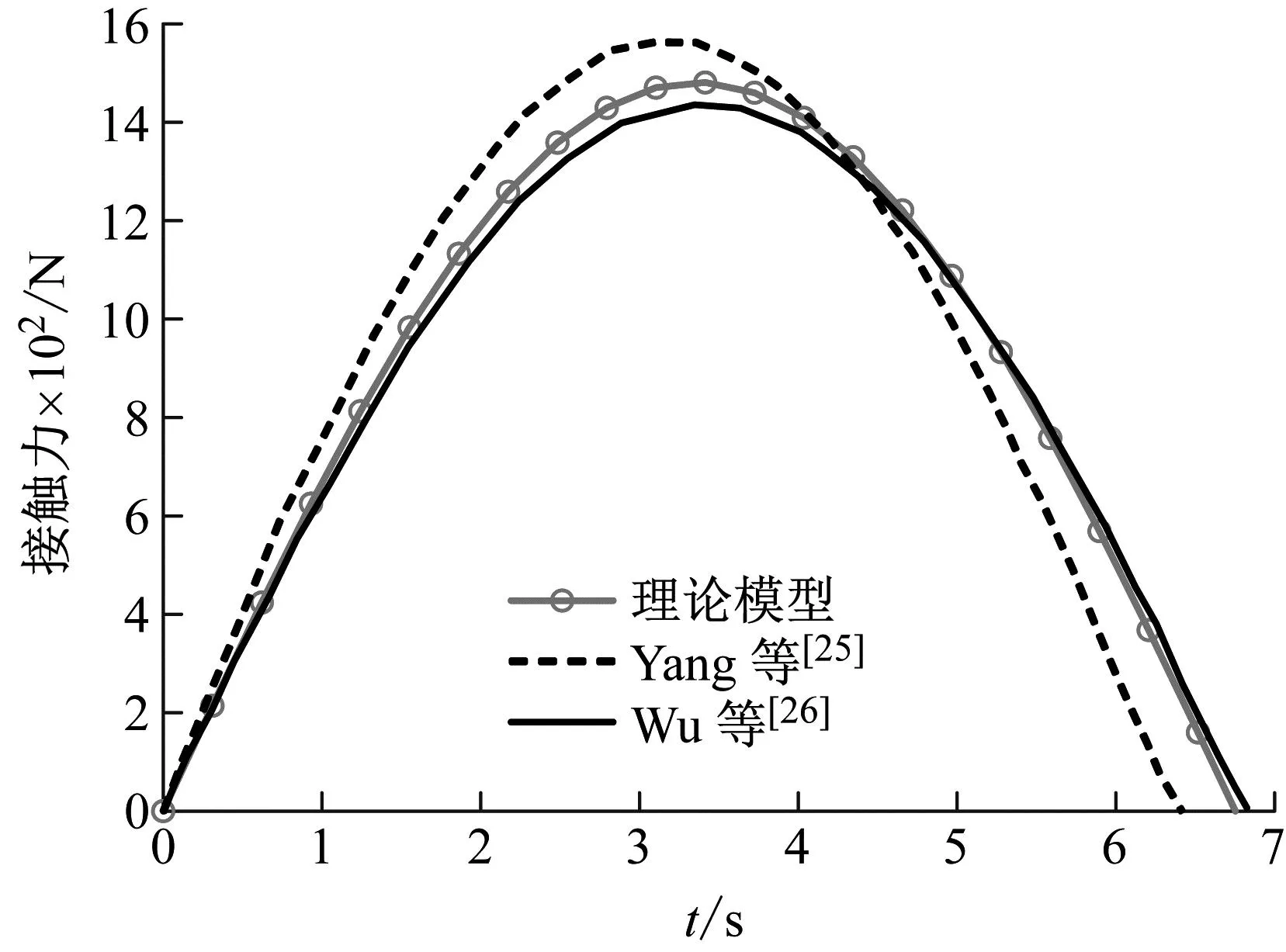
图7 理论模型与参考文献的接触力随时间变化的对比
2 蜂窝夹芯板的参数分析
在本章中,本文通过所建立的理论模型来研究低速冲击下蜂窝胞元的不同几何参数对圆弧形蜂窝夹芯板动力响应的影响。假设圆弧形蜂窝夹芯板材料的密度ρ=2 700 kg/m3,弹性模量E=69 GPa和泊松比μ=0.3,蜂窝夹芯板的长度和宽度为Lx=Ly=100 mm,高度hc=10 mm,顶部蒙皮层和底部蒙皮层高度相等且为1 mm。蜂窝胞元角度θ=45°,蜂窝胞元半径Rc=6 mm,蜂窝胞元壁厚d=2 mm。球形冲击器的半径为10 mm,冲击速度为8 m/s,冲击器材料的密度ρ=7 971.8 kg/m3,弹性模量E=200 GPa,泊松比μ=0.3。
2.1 蜂窝胞元半径对蜂窝夹芯板动力响应的影响
本文假设蜂窝胞元半径分别为5 mm、6 mm和7 mm,在上述其它几何参数不变的情况下,不同蜂窝胞元半径对蜂窝夹芯板动力响应的影响如图8所示。由图8(a)可知,随着蜂窝胞元半径的增加,蜂窝夹芯板的中心最大横向位移也在不断增加,表明在相同的冲击速度下,蜂窝夹芯板的抗冲击性能反而减小。由图8(b)可知,在相同的冲击速度下,随着蜂窝胞元半径的增大,冲击器与蜂窝夹芯板之间的接触力也在增大。在蜂窝胞元其它参数确定的情况下,随着蜂窝胞元半径的增加,蜂窝胞元呈现出扩张的趋势,进而导致蜂窝胞元的抗冲击性能减弱。在相同的冲击载荷下,当蜂窝胞元半径从5 mm增加至7 mm时,蜂窝夹芯板的中心最大横向位移从0.211 mm增加至0.296 mm,夹芯板的抗冲击性能减少40.28%。冲击器与蜂窝夹芯板之间的接触力从12 161.2 N增加至12 389.3 N,接触力增加1.88%。
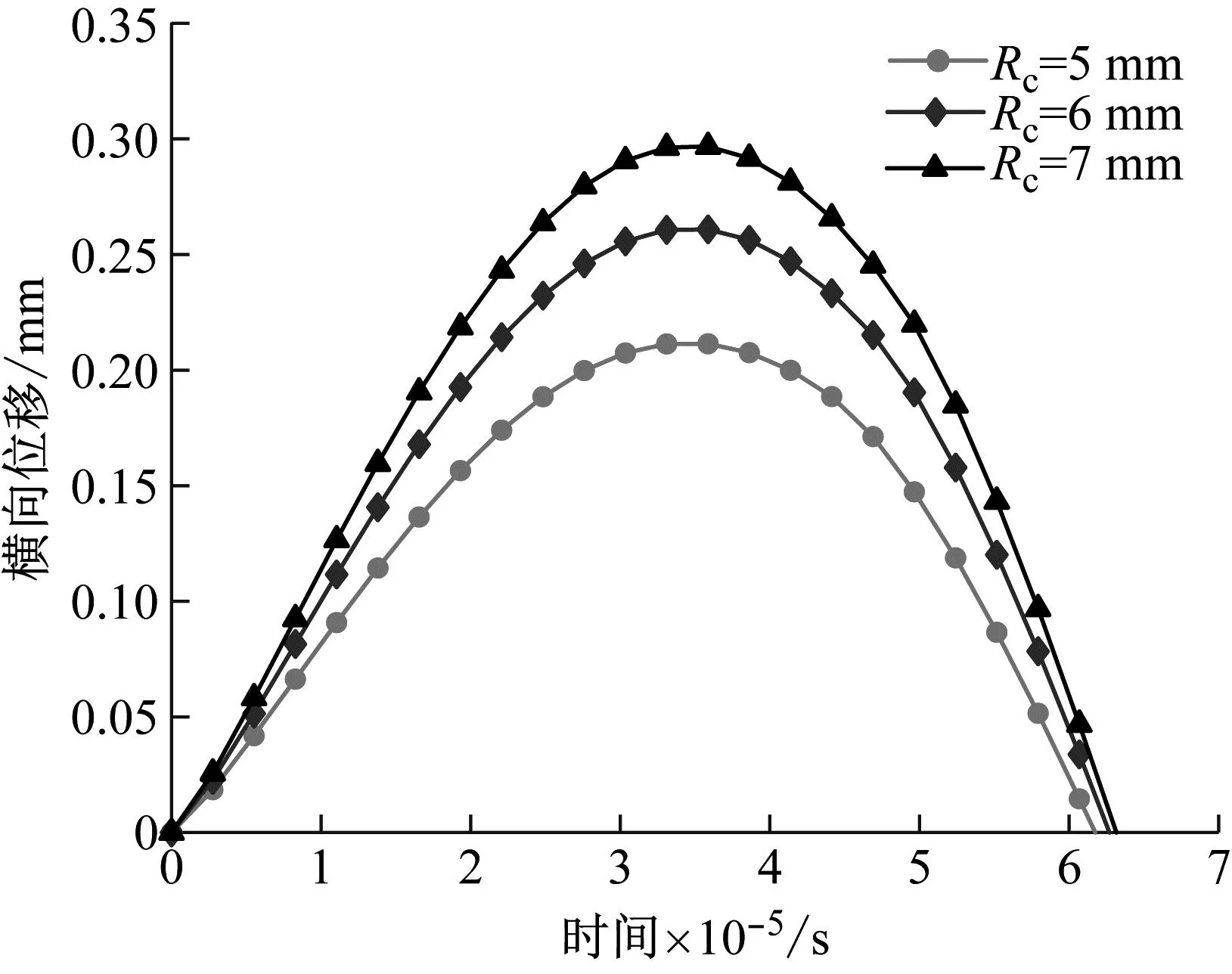
(a) 横向位移随时间变化曲线
2.2 蜂窝胞元角度对蜂窝夹芯板动力响应的影响
本文假设蜂窝胞元的角度分别为30°、45°和60°,在其它几何参数不变的情况下,不同蜂窝胞元角度对蜂窝夹芯板动力响应的影响如图9所示。
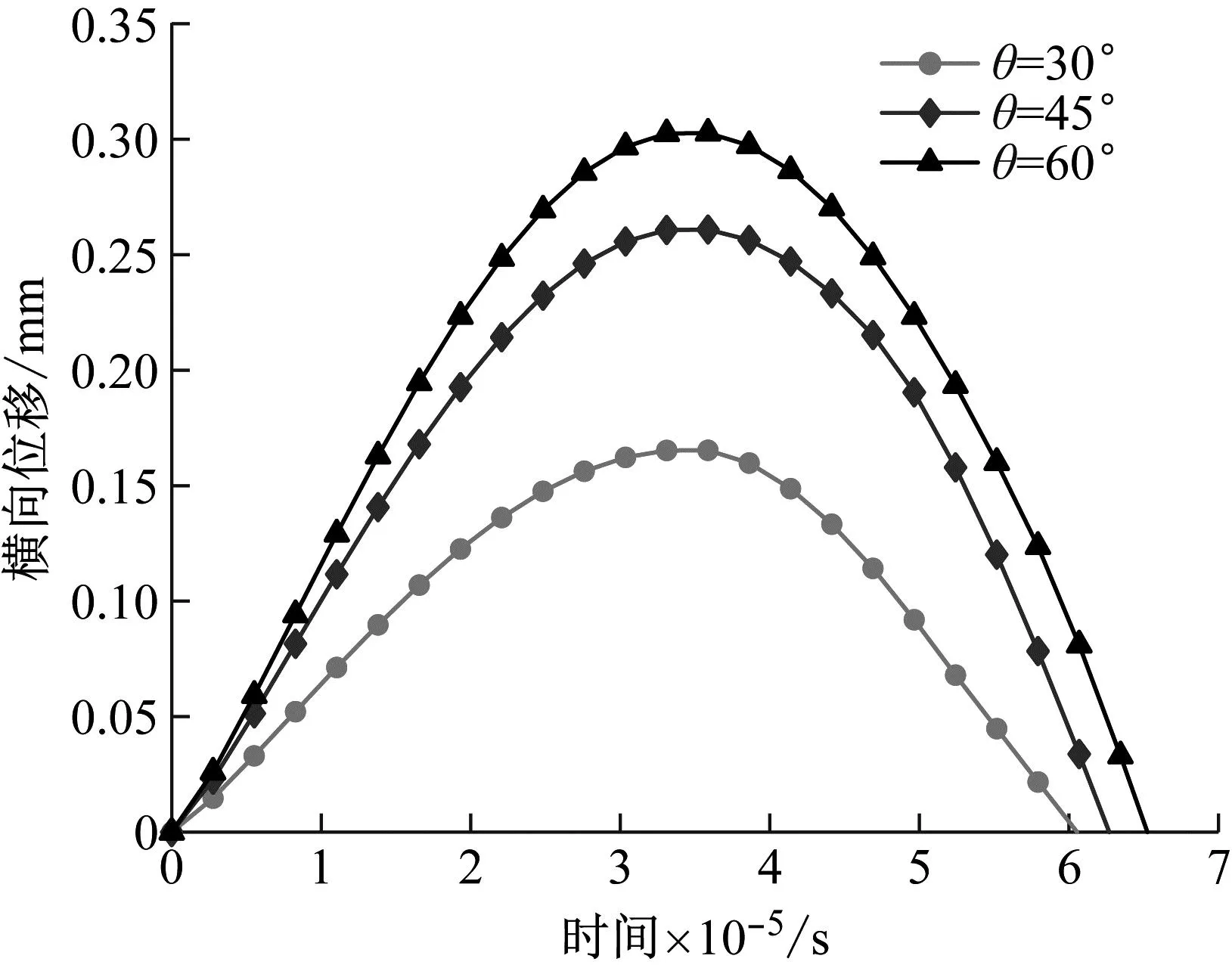
(a) 横向位移随时间变化曲线
由图9可知,在相同的冲击载荷下,圆弧形蜂窝夹芯板的中心最大横向位移随着蜂窝胞元角度的增大而增大。在相同的蜂窝胞元参数下,蜂窝胞元角度的减小可以提升胞元结构的紧密性,使蜂窝胞元呈现出一种收缩的现象,进而提升圆弧形蜂窝夹芯板的抗冲击特性。当蜂窝胞元角度从30°增加至60°时,蜂窝夹芯板的中心最大横向位移从0.165 mm增加至0.303 mm,蜂窝夹芯板的抗冲击性能减少83.64%;蜂窝夹芯板与冲击器之间的接触力从12 184.5 N增加至12 545.5 N,接触力增加2.96%。
2.3 蜂窝胞元壁厚对蜂窝夹芯板动力响应的影响
本文假设蜂窝胞元的壁厚分别为1 mm、2 mm和3 mm,在其它几何参数保持不变的情况下,不同蜂窝胞元壁厚对蜂窝夹芯动力响应的影响如图10所示。由图10可知,在相同的冲击载荷下,圆弧形蜂窝夹芯板的中心最大横向位移随着蜂窝胞元壁厚的增大而减小,当蜂窝胞元壁厚从1 mm增加至3 mm时,蜂窝夹芯板中心最大横向位移0.368 mm减少至0.149 mm,夹芯板的抗冲击性能提升59.51%;蜂窝夹芯板与冲击器之间的接触力从12 524.8 N减少至11 758.8 N,接触力减小6.12%。在蜂窝胞元其它参数确定情况下,蜂窝胞元的壁厚增加可以提升夹芯层与蒙皮层之间的接触面积,进而提升圆弧形蜂窝夹芯板的抗冲击特性。
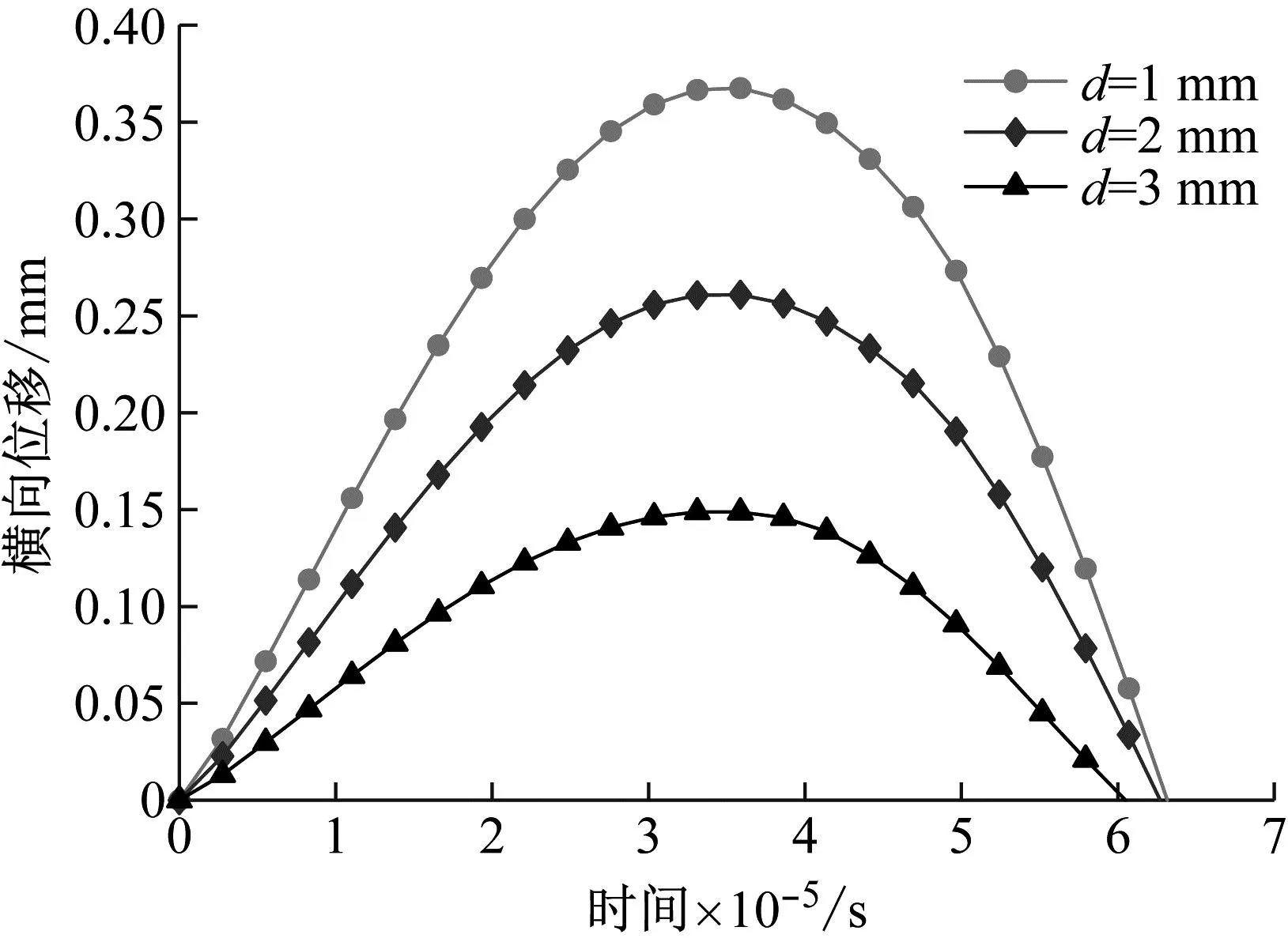
(a) 横向位移随时间变化曲线
2.4 材料密度对蜂窝夹芯板动力响应的影响
假设圆弧形蜂窝夹芯板的长度和宽度为Lx=Ly=100 mm,夹芯层高度hc=10 mm,顶部和底部蒙皮层高度相等且为1 mm。蜂窝胞元角度θ=45°,胞元半径Rc=6 mm,胞元壁厚d=2 mm。本文选用常见的轧制铝、灰铸铁和合金钢作为蜂窝夹芯板的材料,三种材料的参数如表2所示。球形冲击器材料的密度ρ=7 971.8 kg/m3,弹性模量E=200 GPa,泊松比μ=0.3,冲击器的半径为10 mm,冲击速度为8 m/s。

表2 蜂窝夹芯板的材料参数设置
在上述蜂窝夹芯板的材料参数和几何参数设计下,材料密度对蜂窝夹芯板低速冲击下动力响应的影响如图11所示。由图11(a)可知,随着蜂窝夹芯板材料密度的增大,蜂窝夹芯板中心最大横向位移在减小,轧制铝、灰铸铁和合金钢三种蜂窝材料的中心最大横向位移分别为0.261 mm、0.166 mm和0.11 mm,可以得出随着蜂窝夹芯板密度的增大,蜂窝夹芯板的抗冲击特性明显增强。由图11(b)可知,随着材料密度的增大,蜂窝夹芯板与球形冲击器之间的接触力在明显增大。
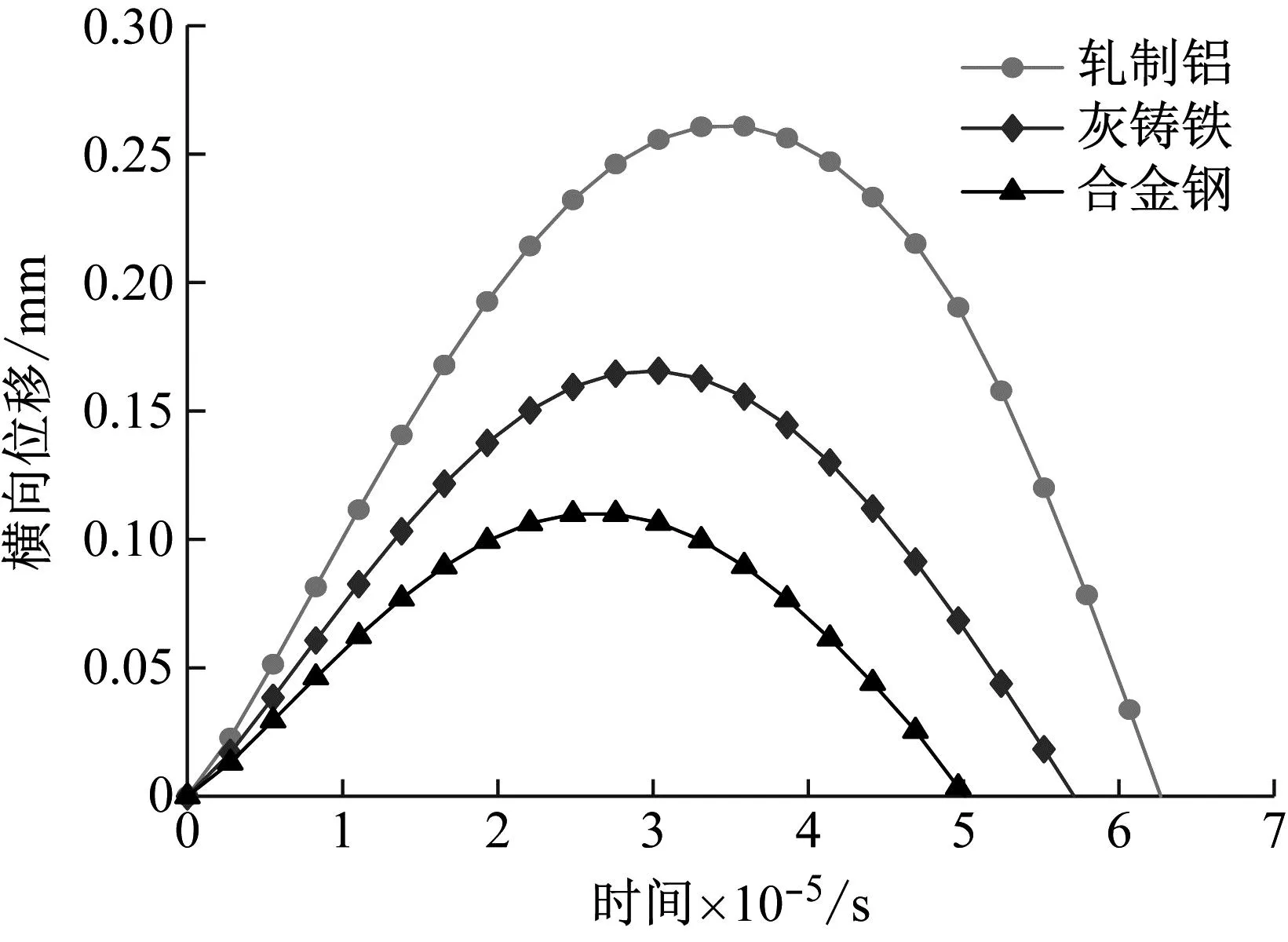
(a) 横向位移随时间变化曲线
3 结 论
(1) 在6种不同冲击速度下理论模型与ABAQUS有限元仿真软件计算出的圆弧形蜂窝夹芯板中心最大横向位移的最大误差为4.9%;在冲击速度为1 m/s时,理论模型与参考文献[25-26]求解出的最接触力的最大误差为8%,验证了当前理论模型的有效性。
(2) 通过理论模型计算出,随着球形冲击器的冲击速度递增,圆弧形蜂窝夹芯板中心最大横向位移也呈现出递增的规律。当冲击速度从4 m/s提升至14 m/s时,夹芯板中心最大横向位移从0.107 mm增加至0.452 mm。
(3) 圆弧形蜂窝夹芯板的抗冲击特性随着蜂窝胞元半径和角度的增大而减小,随着蜂窝胞元壁厚的增大而增大。当蜂窝胞元半径从5 mm增加至7 mm时,蜂窝夹芯板的抗冲击特性减少40.32%;当蜂窝胞元角度从30°增加至60°时;蜂窝夹芯板的抗冲击特性减少80.82%;当蜂窝胞元壁厚从1 mm增加至3 mm时,蜂窝夹芯板的抗冲击特性提升59.57%。
(4) 材料密度对圆弧形蜂窝夹芯板的抗冲击特性也有显著的影响,随着蜂窝夹芯板密度的增加,蜂窝夹芯板的抗冲击特性也会增强。

