分体式双箱梁涡振气动控制措施数值模拟
刘 磊 刘 冲 张 祥
(1.天津城建大学天津市土木建筑结构防护与加固重点实验室,天津300384;2.中交第一航务工程局有限公司,天津300461)
0 引 言
随着悬索桥跨径的不断增长,空气动力稳定性已经成为超大跨度悬索桥加劲梁选型的主导因素。为了改善整体式箱梁断面的颤振稳定性,目前最有效的方法就是将整体式钢箱梁横向分割成两个或多个独立的箱体,形成分体式加劲梁[1-2]。在虎门二桥(现称南沙大桥)主梁断面选型的初步设计方案中提出整体式钢箱梁和分体式钢箱梁两种主梁形式,研究表明分体式钢箱梁开槽处透风率对于主梁颤振稳定和涡振响应存在影响,完全透风对颤振稳定最有利,但是在开槽处会出现明显的涡团,存在增大主梁涡振响应幅值的弊端。
近年来随着分体式箱梁的广泛应用,众多学者对其涡振性能的改善进行了深入研究。王守强[3]进行了不同缩尺比的节段模型涡振风洞试验,研究发现,风攻角、导流板、模型尺度及模型阻尼比会影响涡振位移幅值和涡振风速锁定区间。Larose 等[4]在对昂船大桥分体钢箱梁的涡振试验中发现,导流板通过控制规律性中央开槽处旋涡对结构的驱动,达到制振的目的。张伟等[5]发现,对于分体式箱梁导流板的控制作用与导流板距箱梁底的距离有关。汪正华等[6]分析不同隔涡板透风率对分体式箱梁涡振振幅的影响,发现隔涡板透风率越小抑制涡振的效果越好。王琦等[7]对嘉绍大桥的研究验证了导流板和抑振板的制振效果。杨詠昕等[8]基于粒子图像测速技术的分析表明,中央开槽处的大尺度旋涡很可能是引起大幅度涡振的主要原因。杨詠昕等[9]进一步对比了增大阻尼比、可调风障、导流板和隔涡板4 种控制措施对分体箱梁涡振的控制效果,发现增大阻尼比和增设水平风障可以有效提高分体箱梁的扭转涡振性能,导流板的涡振控制效果与开槽率大小有关;增设0%透风率的隔涡板可以有效降低竖弯涡振振幅。夏锦林等[10]研究发现,均匀间隔的纵向格栅改变了流场绕流特性,阻碍了大规模涡脱的形成,能有效控制涡振。方根深等[11]利用刚体节段模型风洞试验并结合CFD 数值模拟,研究了半开口分离双箱梁的涡振性能,研究发现检修车轨道对竖弯涡振有放大作用,水平翼板和抑流板都能有效控制竖弯涡振。
已有研究对各种气动措施的涡振控制效果大多通过风洞试验数据对比分析得到,对各种气动措施的涡振减振机理,还需要进一步的深入研究。本文采用同济大学刘十一[12]基于非结构化有限体积法自主研发的二维数值模拟平台进行计算,以国内某大跨度悬索桥的涡激共振为背景,对分体式双箱梁(中央开槽)+风障断面的涡振响应进行数值模拟,验证了风障对竖弯涡振控制的有效性。研究了导流板和纵向格栅在一阶正对称竖弯、一阶反对称扭转和七阶竖弯模态,风攻角范围为-3°~+3°情况下的涡振控制效果。最后,基于这三种气动措施的流场特性,对其涡振控制机理进行了研究。
1 中央开槽+风障断面涡振模拟
1.1 工程概况
某悬索桥为主跨1 650 m 的两跨连续钢箱梁悬索桥,主缆分跨为578 m+1 650 m+485 m,主梁采用分体式双箱梁形式,该桥立面图如图1 所示,主梁横断面如图2 所示,动力特性参数如表1 所示。2009 年3 月15 日该桥首次出现加劲梁竖向弯曲涡激共振现象[2],涡振频率约为0.32 Hz,该振动频率对应于第七阶竖弯振型(主梁、主缆竖向弯曲3.5 个波),如图3 所示。涡振过程中加劲梁最大振动幅度约为0.163 m,根据《公路桥梁抗风设计规范》(JTG/T D60-01—2004)[13],该振型对应的容许振幅为0.04/0.32=0.125 m,观测到的涡振振幅超过规范容许值。

图1 某悬索桥立面图(单位:cm)Fig.1 Elevation of target Bridge(Unit:cm)

图2 分体式双箱梁(中央开槽)断面(单位:m)Fig.2 Section of split double box girder(central slotted)of Xiqiaomen Bridge(unit:m)

图3 涡振振型及振幅换算Fig.3 Vortex vibration mode and amplitude conversion

表1 该桥动力特性参数表(通车前)Table 1 Dynamic characteristics parameter table of Xihoumen Bridge(before opening)
1.2 中央开槽+风障断面涡振模拟
该桥涡振发生后,为减小涡激振动对桥梁结构的疲劳影响,改善桥面行车环境,通过设置可变姿态的风障作为涡振控制措施。风障设置于最外侧栏杆之上,风障结构如图4所示。
本文借助同济大学刘十一[12]基于非结构化有限体积法自主研发的二维CFD 数值模拟平台进行计算,断面尺度取实际值。空气密度ρ=1.225 kg/m3,固定动力黏性系数μ=1.5×10-5m2/s,雷诺数Re= ρUB μ,随风速U 变化,B=36 m 为桥梁宽度,计算域尺度为[-734,1 907]×[-1 025,1 025],主梁中心位于(0,0),底层网格三角形边长为0.072 m。设置风障后,主梁断面流场网格划分如图5所示。入口边界条件为指定速度,压强为0,上下壁面指定法向速度为0,不指定切向速度,出口为自然边界,数值模拟的主梁节段模型动力特性参数设置如表2所示。
为了说明数值模拟结果的正确性,表3 给出了风洞试验结果作为比较,从表3 可见,在阻尼比ξ=0.25%的情况下,数值模拟的七阶竖弯模态涡振振幅介于1∶30(Re ≈4×105)和1∶60(Re ≈2×105)节段模型风洞试验结果之间,数值模拟的一阶反对称扭转涡振振幅也介于两个节段模型风洞试验结果之间,说明本文涡振数值模拟结果是可取的。
在风攻角为0°时,将模拟得到的增设风障前、后各模态涡振位移时程曲线绘于图6 中,模拟结果表明风障对一阶正对称竖弯和七阶竖弯模态的涡振控制效果较好,涡振振幅减小50%以上;但对扭转涡振振幅具有一定的放大作用,但振幅仍小于规范容许值。

图4 风障结构图(单位:mm)Fig.4 Wind barrier structure diagram(Unit:mm)
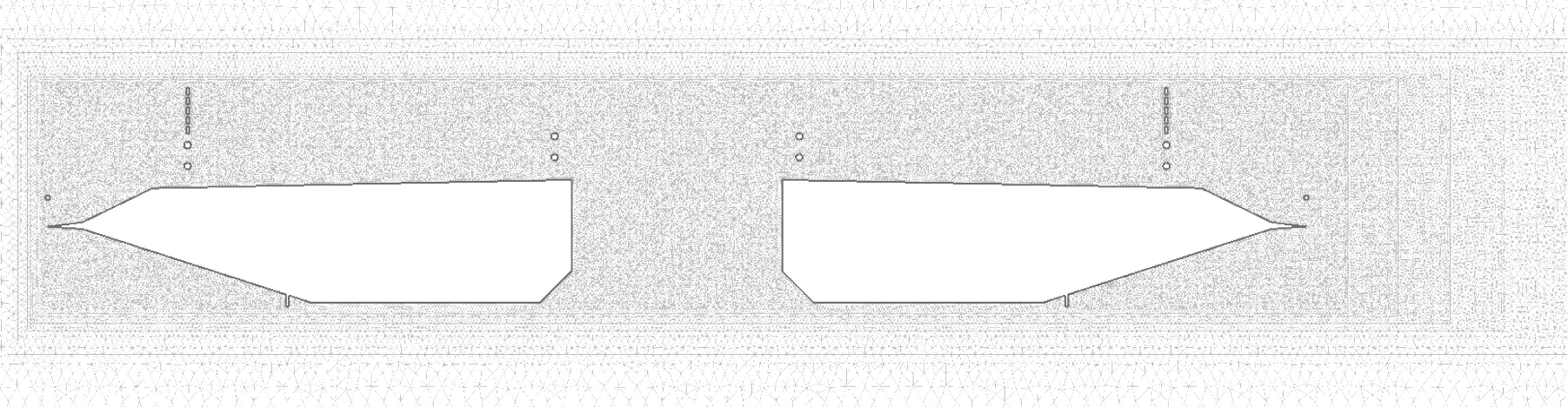
图5 中央开槽+风障断面流场网格划分Fig.5 Central slotting+wind barrier section flow field meshing
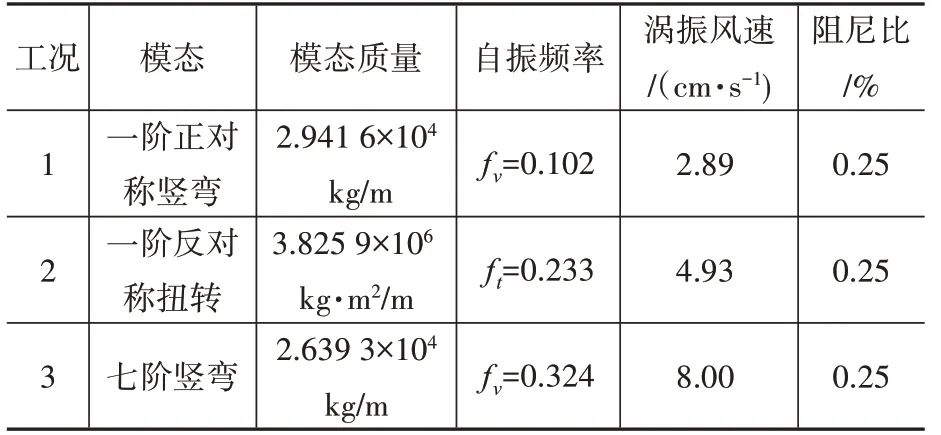
表2 主梁节段模型动力特性表Table 2 Main beam section model dynamic characteristics table

表3 最大涡振振幅数值模拟结果和风洞试验结果比较Table 3 Comparison of numerical simulation results of maximum eddy vibration amplitude and wind tunnel test results
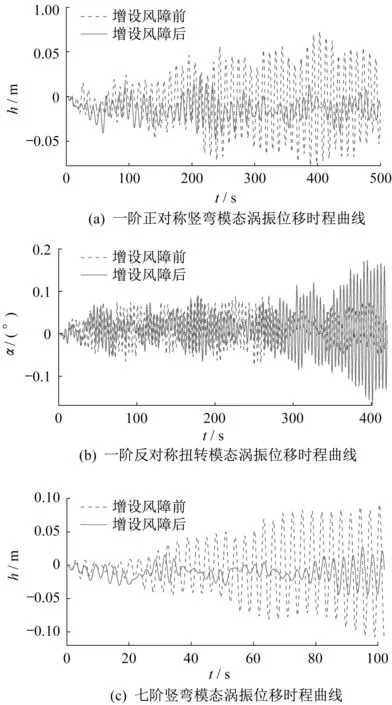
图6 增设风障前、后各模态涡振位移时程曲线Fig.6 Time-history curve of modal vibration displacement before and after adding wind barrier
对于分体式钢箱梁断面,中央开槽导致了主梁断面与风的接触面增多,风流经中央开槽断面后,旋涡的生成、流动、脱落与再附较其他断面更为复杂多样,产生的涡激力也更大,因此中央开槽断面的抗涡振性能较差,尤其是抗竖弯涡振性能。为了分析中央开槽断面七阶竖弯模态涡振形成机理,图7 给出了中央开槽断面在恒定风速U=8 m/s,风攻角为+1°下的瞬时流场正交涡度分布图。正交涡度是速度场旋转矩阵的特征值,旋转矩阵由应变率张量的极分解获得。正交涡度反映了流场中一点的绝对旋转速度,不受速度场剪切分量的影响,因此可用于辨别边界层内的旋涡相态。由图7 可知,由于栏杆的影响,在上游箱体上表面会交替形成尺度较小的涡旋;下游箱体的上、下表面附近有较强的旋涡,这些旋涡来自于上游箱体的尾流脱落;蓝色旋涡为顺时针方向,在上游箱体的上边缘形成,然后沿下游箱体上表面滑移;红色旋涡为逆时针方向,在上游箱体的下边缘形成,然后沿下游箱体的下表面滑移;这些较大尺度的旋涡在主梁表面交替脱落导致了涡振的发生。

图7 中央开槽断面瞬时流场正交涡度图Fig.7 Orthogonal vorticity diagram of instantaneous flow field in central slotted section
中央开槽断面增设风障后在恒定风速U=8 m/s,风攻角为0°时的七阶竖弯模态涡振瞬时流场正交涡度分布如图8 所示,由图8 可知,上游箱体设置的风障阻碍了贴近上游箱体上表面蓝色旋涡的形成,并使蓝色旋涡向远离箱体方向(上方)移动,减少了旋涡在箱体上表面流动和再附;同时当有较大尺度的蓝色旋涡经过下游箱体上表面时,由于下游箱体风障的作用,使得旋涡分解破碎成较小尺度的旋涡,能量迅速耗散,对于桥面基本不产生影响。
2 中央开槽+导流板断面涡振模拟
增设导流板是另外一种被广泛应用的涡振气动控制措施,导流板气动措施示意图如图9所示。
风攻角为0°时,增设导流板前、后七阶竖弯模态涡振时程曲线如图10 所示,各模态涡振最大振幅随风攻角变化规律如图11、图12 和图13所示。

图8 增设风障后瞬时流场正交涡度图Fig.8 Orthogonal vorticity diagram of instantaneous flow field after adding wind barrier

图9 导流板气动措施示意图Fig.9 Schematic diagram of the pneumatic measures of the deflector

图10 七阶竖弯模态涡振时程曲线Fig.10 Time-history curve of seventh-order vertical bending mode vortex

图11 一阶正对称竖弯模态涡振振幅变化规律Fig.11 Variation law of amplitude of first-order positive symmetrical vertical bending mode vortex vibration
由图10 可知,风速持续一定时间后,导流板才会开始发挥减振作用。由图11、图12 和图13可知,导流板对一阶正对称竖弯模态各攻角下的涡振控制效果不稳定;导流板对一阶反对称扭转模态负风攻角下的涡振具有一定控制作用,涡振振幅减小约25%,但在正风攻角下,其涡振控制效果并不明显;导流板对七阶竖弯模态负风攻角下的涡振具有较好的控制作用,涡振振幅减小约35%,在正风攻角下,其涡振控制效果同样不明显。
为了分析导流板对七阶竖弯模态涡振控制机理,图14 给出了中央开槽+导流板断面在恒定风速U=8 m/s,风攻角为-3°下的正交涡度分布图。由图14 可知,气流经过导流板的压缩后速度得到提高,冲出导流板时这股高速射出的气流打碎了中央开槽部位形成的旋涡,阻碍了较大尺度旋涡的生成。

图12 一阶反对称扭转模态涡振振幅变化规律Fig.12 The variation law of amplitude of the first-order antisymmetric torsional mode vortex

图13 七阶竖弯模态涡振振幅变化规律Fig.13 Variation law of amplitude of vortex vibration in seventh-order vertical bending mode
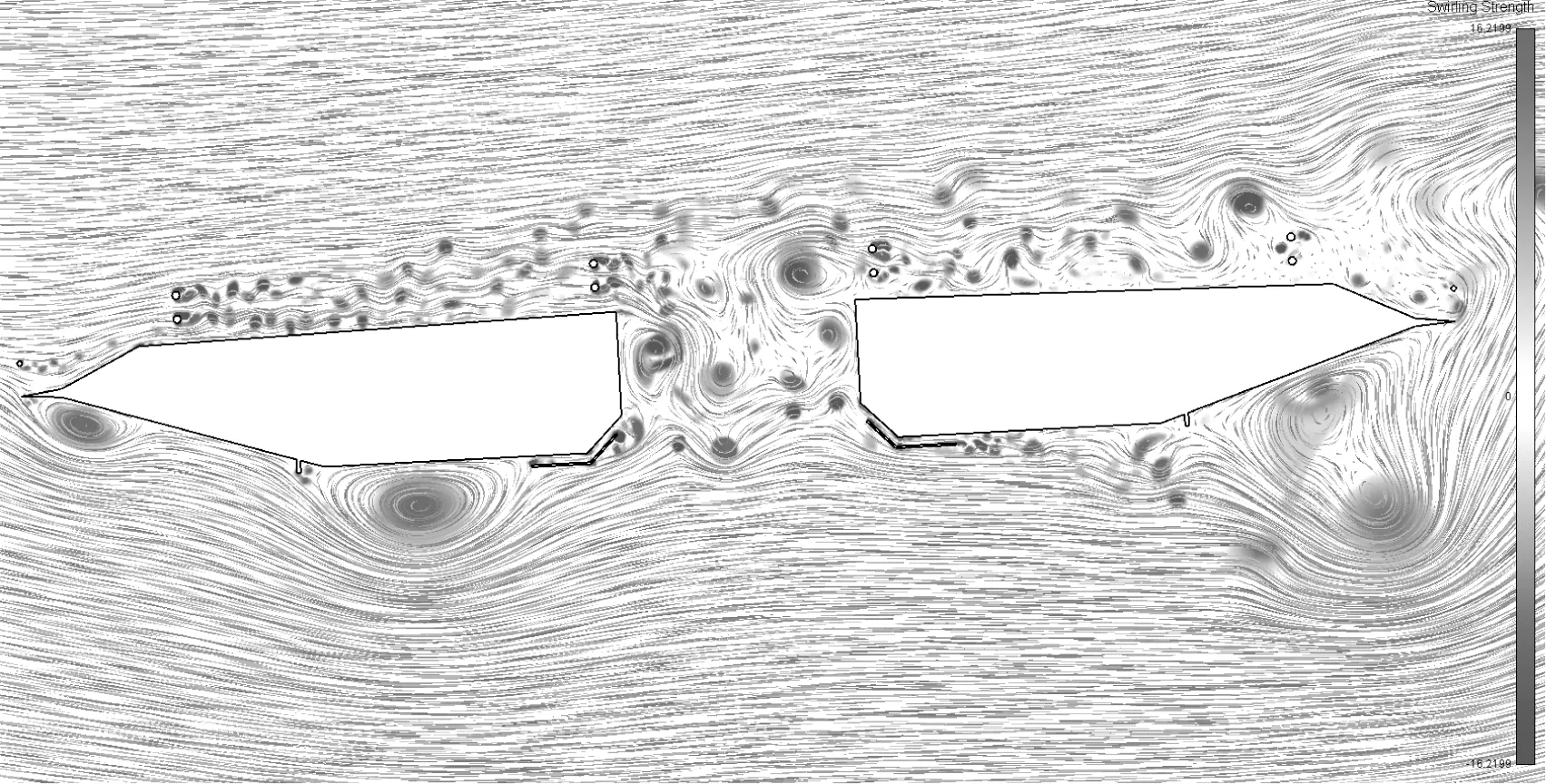
图14 增设导流板后瞬时流场正交涡度图Fig.14 Orthogonal vorticity diagram of instantaneous flow field after adding deflector
3 中央开槽+纵向格栅断面涡振模拟
为了研究纵向格栅的涡振控制效果,在主梁断面开槽处中部共设置10 道纵向格栅,格栅透风率为50%,设置格栅后的主梁断面如图15所示。

图15 纵向格栅气动措施示意图(单位:m)Fig.15 Schematic diagram of pneumatic treatment of longitudinal grille(Unit:m)
风攻角为0°时,增设纵向格栅前、后七阶竖弯模态涡振时程曲线如图16 所示,各模态涡振最大振幅随风攻角变化规律如图17、图18 和图19所示。

图16 七阶竖弯模态涡振时程曲线Fig.16 Time-history curve of seventh-order vertical bending mode vortex

图17 一阶正对称竖弯模态涡振振幅变化规律Fig.17 Variation law of amplitude of first-order positive symmetry vertical bending mode vortex vibration
由图17、图18 和图19 可知,纵向格栅对一阶正对称竖弯、一阶反对称扭转和七阶竖弯模态在各攻角下的涡振均具有很好的控制效果。增设纵向格栅后,一阶正对称竖弯涡振振幅减小约20%,一阶反对称扭转振幅减小约35%(0°攻角除外);七阶竖弯模态在负攻角下涡振振幅减小约65%,在正攻角下涡振振幅减小约30%。

图18 一阶反对称扭转模态涡振振幅变化规律Fig.18 The variation law of amplitude of the first-order antisymmetric torsional mode vortex

图19 七阶竖弯模态涡振振幅变化规律Fig.19 Variation law of amplitude of vortex vibration in seventh-order vertical bending mode
中央开槽+纵向格栅断面在恒定风速U=8 m/s,风攻角为0°时,七阶竖弯模态涡振瞬时流场正交涡度分布如图20所示。由图20可知,纵向格栅有效控制了中央开槽部位较大尺度旋涡的形成;上游箱体上表面脱落的蓝色旋涡和上游箱体下表面脱落的红色旋涡流经纵向格栅后会被格栅打碎分解成很小尺度的旋涡,从而控制了涡振的发生。

图20 增设纵向格栅后瞬时流场正交涡度图Fig.20 Orthogonal vorticity diagram of instantaneous flow field after adding vertical grid
4 结 论
(1)对于分体式双箱梁而言,风障可以有效降低竖弯涡振振幅,但可能会放大扭转涡振振幅;导流板的涡振控制效果与风攻角和涡振风速有关。导流板在负攻角下的涡振控制效果较好,在正攻角下的涡振控制效果不好。
(2)导流板对分体式双箱梁在负攻角下的涡振控制效果随风速增大而加强,这可能是由于高风速下的气流经过导流板高速压缩后速度会得到更大提高,冲出导流板时这股高速射出的气流会较强地干扰开槽处较大尺度旋涡的生成,从而抑制涡振发生。
(3)纵向格栅对分体式双箱梁在各攻角下的一阶正对称竖弯、一阶反对称扭转和七阶竖弯涡振均有很好的控制效果。

