基于LINGO及虚功原理的框架—核心筒结构优化研究

朱杰江 陆佳慧 张 磊

（上海大学土木工程系，上海200072）

0 引 言

框架-核心筒结构体系是高层建筑常采用的一种结构形式，与框架-剪力墙结构体系一样，其框架部分可满足结构的灵活布置以及较大的空间，同时其筒体结构的抗侧刚度也优于一般的框剪结构中的剪力墙。因此高层框架-核心筒能承担较大的水平效应并在经济上优于框架-剪力墙结构。

在现有的框架-核心筒设计中，由于缺乏技术规范对其明确的约束要求，在设计中往往会放大安全系数以保证结构安全性，从而在经济合理性上造成了浪费。目前对于框架-核心筒的优化研究较少，且目标函数多为结构刚度或地震作用，王全风等［1］在已知材料和结构形式的条件下，基于地震荷载对框剪结构进行了剪力墙数量的优化；侯胜利等［2］以结构第一周期最小为目标，以构件尺寸为变量对某超高层框架-核心筒结构进行优化；陈跃等以最大层间位移角为目标，对等、变截面框筒结构中加强层的位置进行了优化［3］。本文将以造价为目标函数，采用VB 语言和调用成熟的优化软件LINGO 进行编程，对结构的抗侧力体系进行优化。

1 框架-核心筒结构优化模型

1.1 优化变量

构件尺寸对于降低结构造价具有决定性作用。假设框架-核心筒结构第k 层标准层，有m 组柱、n 组梁、s 组剪力墙，则优化对象为梁和柱的截面高度与截面宽度、剪力墙的墙厚与墙长。

构件材料也是决定最终造价的关键性因素。每一层附加一个层混凝土强度等级的设计变量，混凝土强度等级作为每一楼层的柱和剪力墙的变量，本文提供了C30～C50 的选择。不对梁的混凝土强度进行优化是因为对于采用现浇楼板的结构，为便于施工，梁的混凝土强度等级一般与楼板的混凝土强度等级相同。为避免因混凝土强度过高而增加楼板因温度变化和收缩引起裂缝的可能性，故《高层建筑混凝土结构技术规程》（JGJ 3—2010）第3.2.2条第7款规定“现浇非预应力混凝土楼盖结构的混凝土强度等级不宜高于C40”。构件的配筋是关于构件截面尺寸的函数，因此最终的优化设计变量仍是截面尺寸。

综上，对于楼层k，共有设计变量总数为2m+2n+2s+1个。

1.2 目标函数

本文的目标函数为结构竖向总造价，即为所有竖向构件造价之和。

（1）单根梁造价由混凝土、纵筋、箍筋、模板构成，其表达式为

式中：bi，hi为构件截面宽与高；Cc为混凝土单位体积价格；Cm为模板单位面积价格；li为构件长度；ρs为钢筋密度；Cs为钢筋单位重量价格；As为上下架立筋面积之和；As1、As2为梁端支座纵筋面积；Asv为箍筋面积；lsv为箍筋长度；n为箍筋根数。

（2）单根柱的造价由混凝土、纵筋、箍筋、模板构成，其表达式为

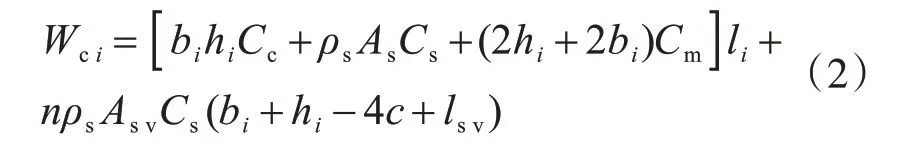
式中：c 为混凝土保护层厚度；lsv为柱的内部箍筋长度。

（3）单片墙的造价主要由混凝土、纵筋、箍筋、拉筋、模板构成，其表达式为

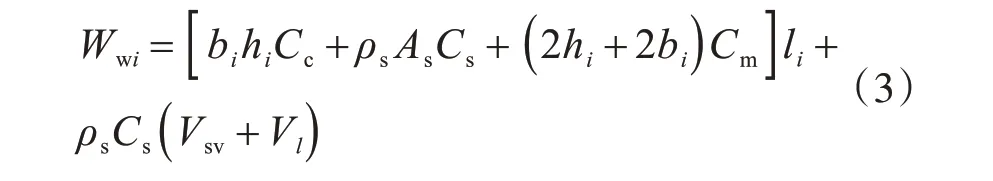
式中，Vsv，Vl分别为箍筋和拉筋体积。

则总的表达式为

式中，nb、nc、nw 分别为结构中框架主梁、框架柱、剪力墙的总数。

1.3 约束条件

构件约束条件依据《混凝土结构设计规范》等规范［4-5］列出，主要包括强度约束、刚度约束和构件的构造约束等，在其中筛选出主要控制因素。其中，强度约束用以梁、柱的配筋计算，而剪力墙依据规范要求进行构造配筋。

1.3.1 强度约束

框架梁柱的强度约束条件为

式中：M、V 为截面承受的弯矩和剪力；Mu、Vu为截面最大弯矩设计值、剪力设计值。

1.3.2 刚度约束

框架-核心筒结构最大层间位移角约束条件：

式中，δi为第i层层间相对位移；hi为第i层层高。

1.3.3 构造约束条件

梁的主要约束条件有截面受压区高度约束、截面高宽比约束、受剪截面约束、连梁约束和支座与跨中的最小配筋率约束。

柱的主要约束条件有轴压比约束、截面高宽比约束、受剪截面约束、最小及最大配筋率约束和加密区箍筋构造要求。

墙的主要约束条件有轴压比约束、受剪截面约束和构造配筋要求。

1.3.4 层间约束条件（自下而上）

（1）本标准层的混凝土等级不小于上一标准层的混凝土等级，且相差不超过两级；

（2）本标准层竖向构件尺寸不小于上一标准层相连竖向构件的尺寸；

（3）平面上同一位置的框架柱截面尺寸b、h不小于上一层柱截面尺寸；

（4）平面上同一位置的剪力墙墙厚IB 不小于上一层墙厚，墙长在竖向上是相同的。

2 程序优化流程及原理

2.1 优化流程及所需软件

本文用ETABS 进行初始三维有限元模型的建立，进行内力分析；然后使用VB 语言编写前处理模块，利用ETABS API接口获取模型构件信息，完成规范所需要的内力调整；将构件信息、内力设计值及虚功等信息输出LINGO 进行优化求解；优化完成后返回新的设计变量值，修改ETABS 模型，进行下一轮优化计算，直至目标函数收敛，收敛条件为，对于k次循环，结构总造价Wk满足循环判定条件|Wk-Wk-1|≤Δ，Δ为事先给定的小正数。流程图如图1所示。

LINGO 软件是一种科学计算软件，用于求解非线性规划、线性规划等最优化问题，其优势在于有内置的建模语言，使用简单、操作灵活，计算执行速度快［6］，因此作为一款成熟的优化软件相比于自行编译的优化程序，提高了优化模块的效率。LINGO 用于读取主控程序生成的内力文件进行优化，将优化结果生成程序返回主控程序。主要采用的方法为序列线性规划法（SLP），将非线性规划问题转化为线性规划问题，利用单纯形法对其求解［7］。

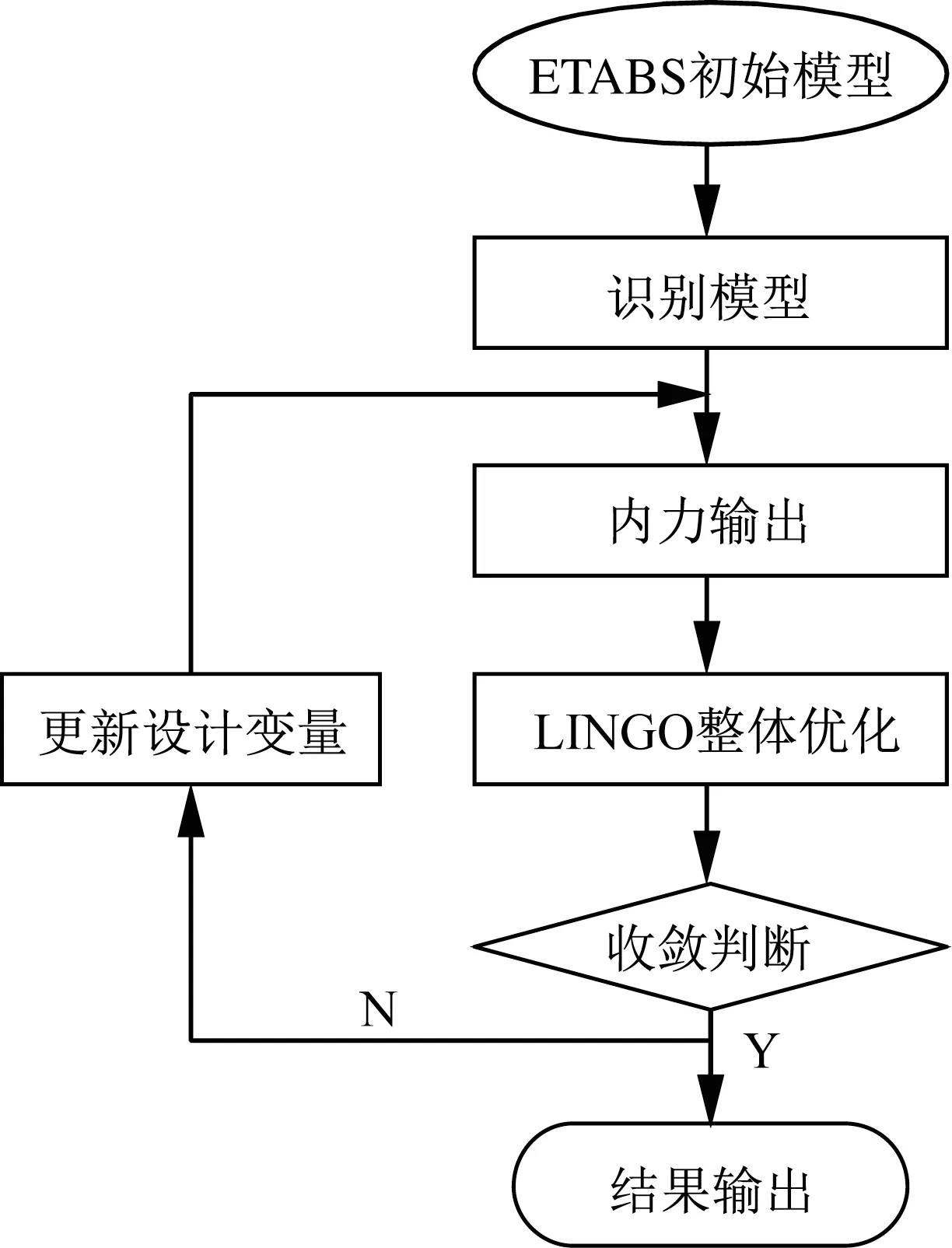
图1 整体优化程序流程图Fig.1 The flow chart of whole optimization program

2.2 VB主控程序

使用VB 语言编写的主控程序主要用于模型信息的处理和整合，即处于LINGO 优化模块之前的控制程序。具体流程为：首先对选定的ETABS模型文件进行识别，统计构件标签、截面类型、节点标签、坐标信息，进行构件分组和标准层划分，目的是提高优化程序的效率；然后在角点添加X、Y 向单位力用于虚功计算，获取实际的层间位移角，控制ETABS 进行内力计算分析，根据规范调整结构内力，提取各组构件中最不利荷载组合；最后将数据输出给优化程序进行优化。

程序的输入界面主要包括三大部分：构件数据用于后期构件的分组以及标准层的划分；材料单价根据当地的定额计算指标计算得到；设计基本参数是为了在程序的内力计算时根据中国规范做出相应的内力调整，包括“强柱弱梁、强剪弱弯、强节点弱构件调整”以及抗震能力系数调整等。

此外为了提高优化效率，本文对主控程序还做出了以下调整：由于在高层建筑结构中，除了底部几层外，其余楼层的竖向构件（框架和剪力墙）基本根据构造条件来进行配筋设计，因此本文程序对剪力墙和柱只进行了计算轴压比需要的内力提取；内力提取时，选择需要的荷载组合，排除非主要控制条件的荷载组合。

图2 虚功原理示意图Fig.2 The diagram of virtual work principle

2.3 虚功原理

在以往的结构优化中，广泛使用的准则法无法与位移约束同时考虑［8］，常常把位移约束和强度约束分开进行独立优化，而忽略了两者之间的相互影响也降低了优化效率。本文尝试使用虚功原理将层间位移显式地表达出来进行整体优化，同时考虑混凝土等级为变量，使最后的优化结果一次性满足强度约束和位移约束。

如图2 所示，在结构上某一点K 点施加单位集中力FK=1，引起的支座反力为，结构中某一微段上的内力为。而实际状态中K 点位移为∆K，支座位移为c，微段上的相应变形为dμ、dφ、γds，根据虚功原理有：

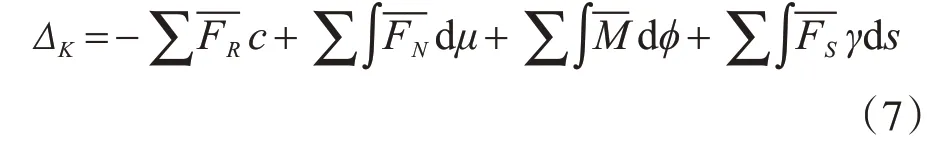
为了进行结构优化的数值计算，需要将结构的位移值显式地表达出来，所以根据虚功原理推导出框架-核心筒结构中某一位置的具体位移表达式为：

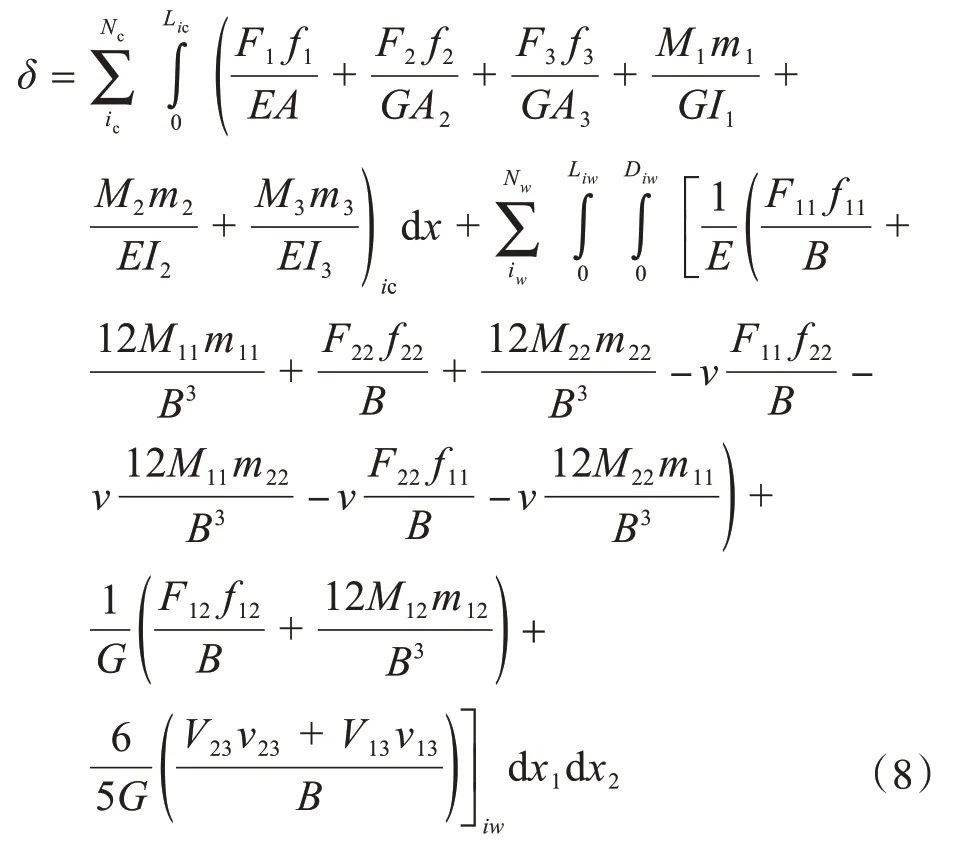
式中：E、G 为构件的弹性模量和剪切模量；v 为混凝土泊松比；B 为截面宽度或厚度；A 为构件截面面积，A2、A3、I1、I2、I3为截面的相关特性；F1、F2、F3、M1、M2、M3为框架梁和柱在某一工况下的截面内力，f1、f2、f3、m1、m2、m3为框架构件梁和柱在同一位置处的单位荷载下的截面内力；F11、F22、F12、V13、V23、M11、M22、M12为剪力墙在某一工况下的截面内力，f11、f22、f12、v13、v23、m11、m22、m12为剪力墙在同一位置处的单位荷载下的截面内力。

简化表达式为

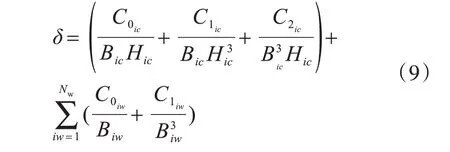
式中：

式中：δcs为cs 层的位移值；δcs-1为cs-1 层的位移值；hcs为cs层层高。

同一层不同位置点的位移不尽相同，为了降低位移约束个数从而减少运算量，程序选择每层层间位移角最大位置——角柱节点的层间位移角进行位移约束，即每一层共4 个控制点，根据施加的荷载，每个控制点分别由地震作用和风荷载引起X、Y两方向的层间位移。

3 算 例

3.1 模型信息

某30 层框架-核心筒结构，关于X 轴与Y 轴对称，平面尺寸如图3 所示。每层层高4.0 m，抗震设防烈度为7 度（0.10 g），地震分组为第一组，特征周期为0.9 s，框架抗震等级为二级，剪力墙抗震等级为二级，基本风压0.55 kN/m2，地面粗糙度C 类，楼面附加恒荷载为2.5 kN/m2，活荷载为2.0 kN/m2，框架梁上线荷载为8.5 kN/m2。

3.2 优化结果

初始模型在整体结构刚度上有很大富余，结构的刚度有较大的下降空间，即该模型有一定的优化空间。由于该结构较高，为减少优化变量数目，划分为3 个标准层，每层10 层，每个标准层内进行构件分组，分组名称见表1，优化前后的构件尺寸。

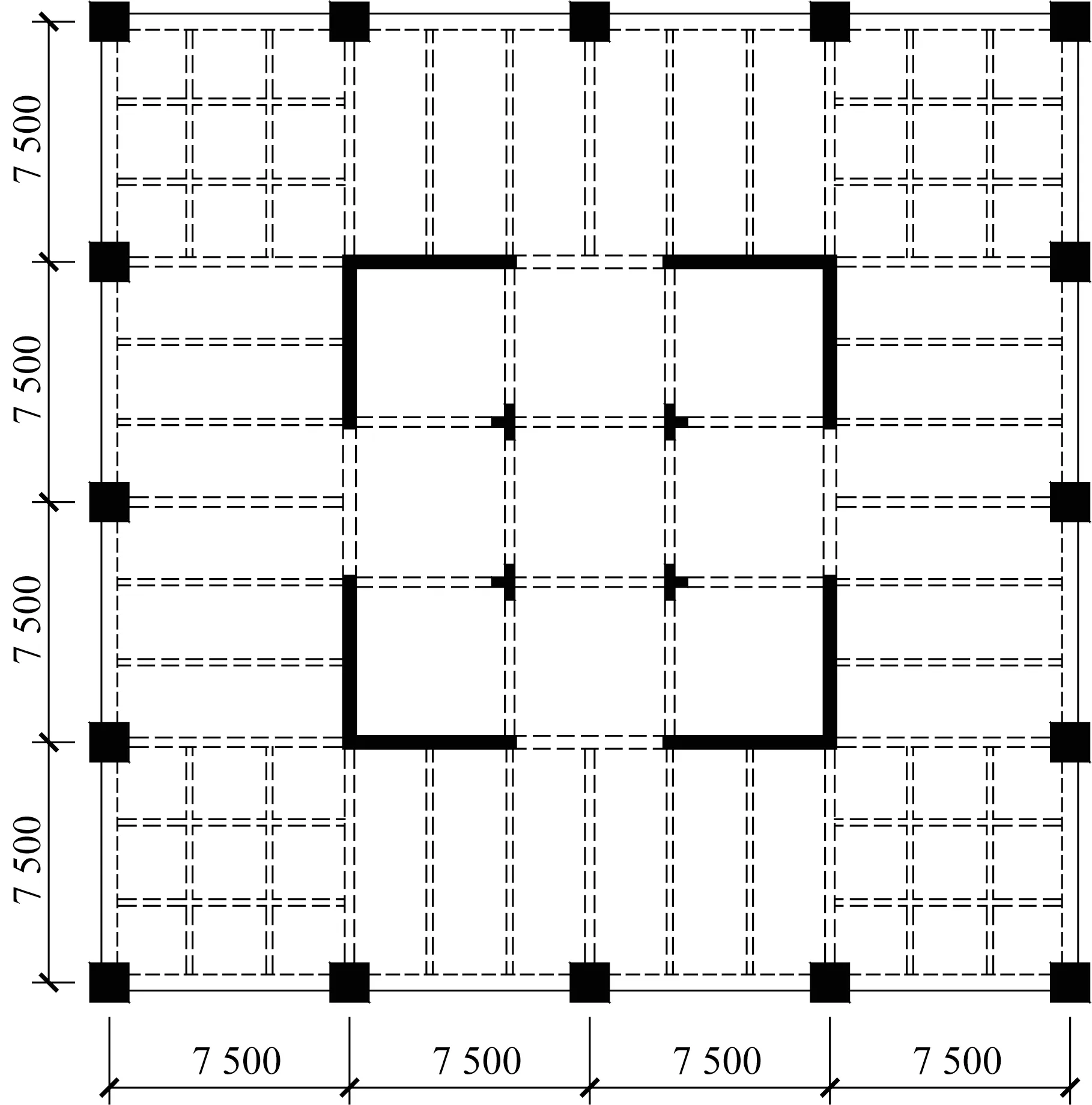
图3 初始标准层平面简图（单位：mm）Fig.3 The initial plan of standard floor（Unit：mm）

表1 优化前后的构件尺寸Table 1 The component sizes before and after optimization m

在地震作用和风荷载作用下，优化前后的层间位移角见表2。由于结构对称，X、Y向施加的荷载相同，结构在X、Y 向的作用响应也应该是近似的，故表中只选取了X 向的层间位移角。优化以后，各层层间位移角都相应增大，结构刚度降低但满足了整体位移约束条件。

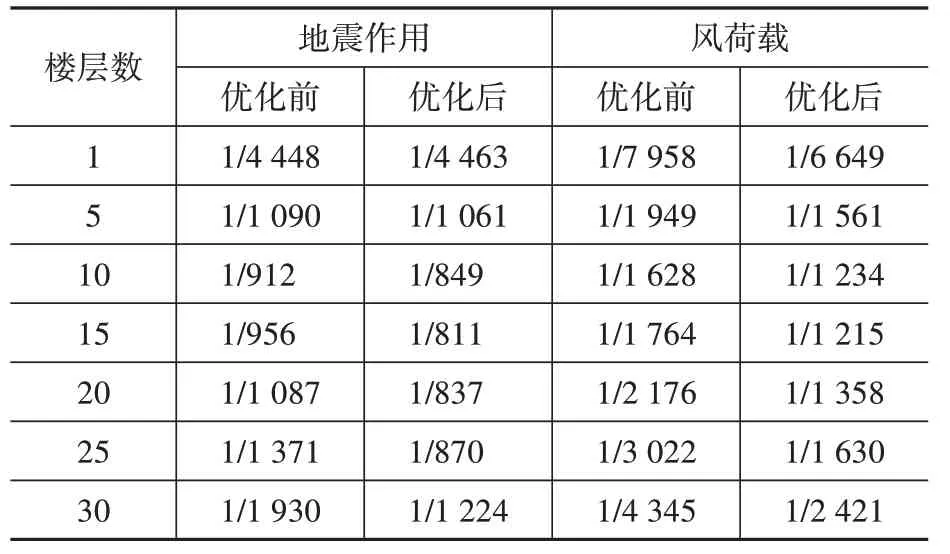
表2 优化前后的层间位移角Table 2 The story drift before and after optimization

整个优化过程共进行了8 次计算，优化总时长近30小时。总造价的迭代曲线如图4所示。优化后，整个结构造价比初始节省了20.1%。

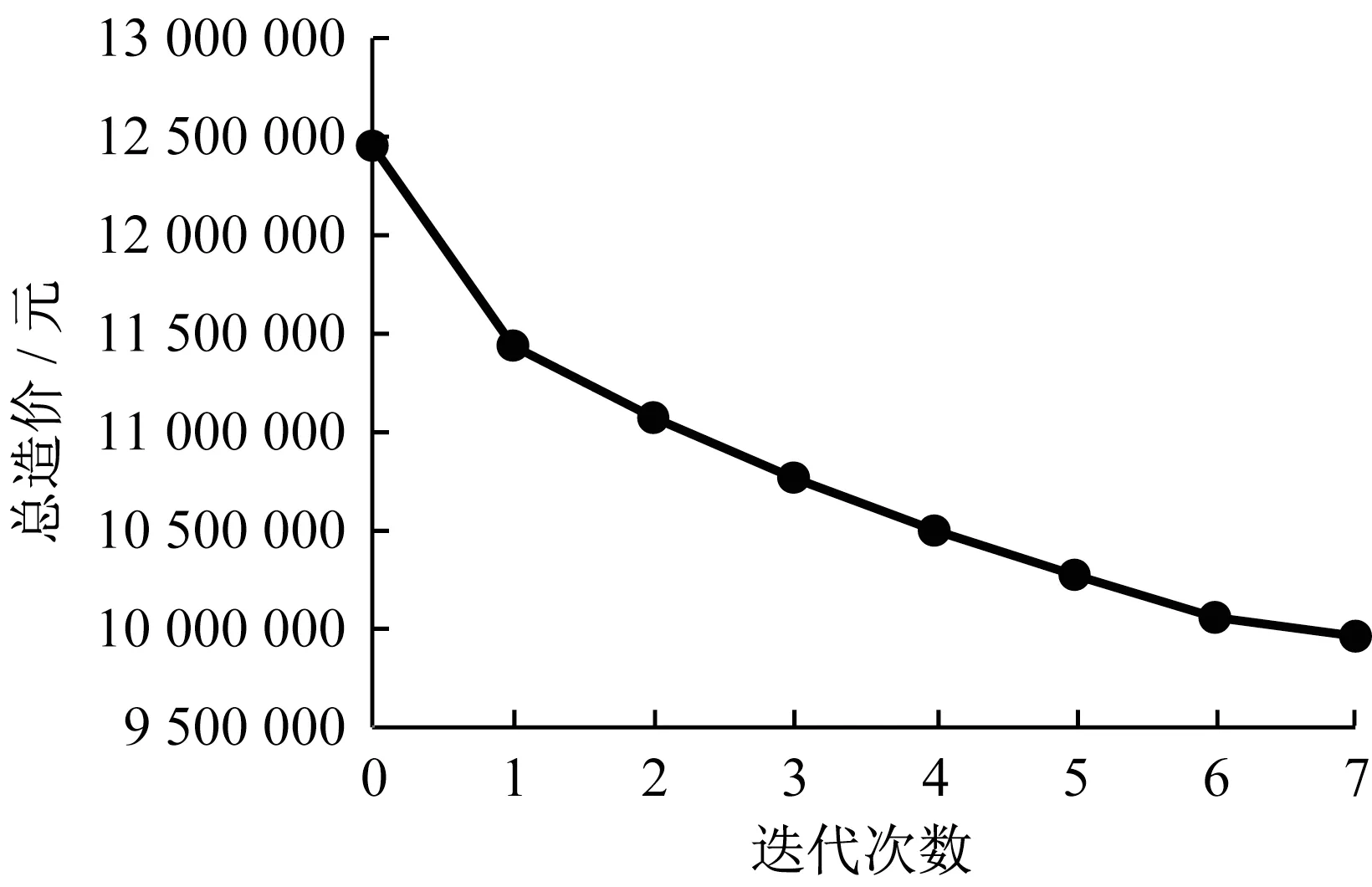
图4 总造价优化曲线Fig.4 The optimization curve of total cost

整个优化程序运行速度较快，主要原因归结于：成熟的优化软件LINGO；标准层划分以及构件的分组；控制条件的筛选：主梁为强度约束，而剪力墙和框架柱为剪压比、轴压比及位移角的约束，抓住了高层结构的主要矛盾，降低了约束条件的数量。

4 结 论

本文基于LINGO 优化求解器对框架-核心筒结构进行了造价优化，用VB 语言编写了相应的程序。LINGO 作为成熟的优化软件可以提高优化收敛的速度，使优化程序拥有更高的优化效率。同时以虚功原理有效地进行了位移计算，提高优化的精度，但是虚功数据量大，结构复杂、构件数量多时会大大增加优化时间。本文通过算例验证了优化程序的可行性，为结构初期的优化设计提供了一个经济的方案。