基于流形特征域适配的滚动轴承故障诊断
周宏娣,黄 涛,李 智,钟 飞
(湖北工业大学 机械工程学院,武汉 430068)
轴承是旋转机械中的关键零部件之一,其通常在变工况、多工况条件下运行,极易发生故障,一旦出现故障,轻则影响整个系统的稳定运行,重则造成经济损失和安全事故[1-2]。因此,实现轴承在复杂工况下的故障诊断具有重大的工程意义[3]。
工程实际中获取的设备状态信号通常正常状态居多、标签稀缺且故障信息不全,导致智能诊断算法性能受限[4]。迁移学习[5]能够复用旧知识解决新场景下的新问题,弥补目标域的典型故障信息缺失等问题,被广泛应用于跨工况条件下的故障诊断[6]。Dong等[7]结合深度学习的特征提取能力,以统计分布和几何空间联合调整适配两域分布,解决了变工况条件下故障诊断效果差的问题。曹洁等[8]提出了一种改进残差网络的领域自适应故障诊断方法。Pan等[9]提出迁移主成分分析(transfer component analysis,TCA)算法,在公共子空间中可最小化源域和目标域间的差异,田威威等[10]将TCA应用于滚动轴承故障识别。上述方法通过域分布适配以解决变工况下的故障诊断问题,取得了较好效果。然而,当两域特征分布差异较大时,仅进行域分布适配难以应对轴承在多工况条件下产生的复杂分布差异[11]。
数据流形局部几何结构中具有潜在的判别性信息,在进行域适配时对数据固有流形特征挖掘,可应对变工况下产生的复杂分布差异,被广泛应用于故障诊断[12-13]。Wang等[14]在无监督领域自适应中引入流形对齐,从而减小源域与目标域的分布位移和结构偏移。沈长青等[15]通过在格拉斯曼流形中构建测地线流式核(geodesic flow kernel,GFK),提取故障信息相关流形特征,来减小数据之间的分布不一致和扭曲。刘海宁等[16-17]在子空间中对故障特征进行流形特征变换,从而减小域间特征偏移。上述方法利用流形学习获取特征表示,但在模型跨域故障识别时,仅对源域与目标域进行域分布对齐,未从局部和全局角度定量评估特征之间相关性,无法有效解决特征扭曲与域间数据偏移的问题。
针对以上问题,本文提出一种基于流形特征域适配(manifold feature domain adaptation,MFDA)的滚动轴承故障诊断方法。首先,利用源域数据无监督地生成与目标域具有相似分布的中间域,构建与源域、中间域和目标域相关的公共子空间。在公共子空间中,利用基于拉普拉斯特征映射(Laplacian Eigenmaps,LE)的局部生成差异度量保留数据流形局部几何结构,减小数据间局部域差异,避免特征扭曲与发散;其次,采用最大均值差异度量对数据进一步对齐,从全局角度最小化中间域和目标域间的分布差异,保证数据之间局部与全局结构的一致性。最后,通过迭代更新样本特征伪标签,以最小二乘法为分类器实现滚动轴承的跨域故障识别。在三个滚动轴承数据集进行试验,验证了所提方法的有效性和优良泛化性能。
1 流形特征域适配
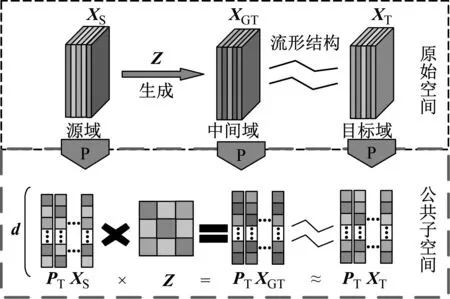
图1 流形特征域适配示意图
1.1 局部生成差异度量
在原始空间中,源域和目标域特征分布不一致,直接对原始数据进行迁移可能会导致数据扭曲,可以通过投影矩阵将其映射到一个公共子空间上,利用源域无监督的生成一个与目标域具有相似分布的中间域φ(XGT),并以基于LE的局部生成差异度量(local generative discrepancy metric,LGDM)保留数据流形局部几何结构,从局部角度减小域间差异,提高中间域φ(XGT)和目标域φ(XT)的分布一致性,φ(XGT)和φ(XT)之间的局部联系可定义为
(1)
式中:DGT和DT为中间域和目标域的分布;Wp,q为邻接矩阵W。Wp,q为
(2)
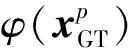
(3)
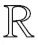
1.2 最大均值差异度量
最大均值差异(maximum mean discrepancy,MMD)能在数据全局分布中有效评估数据分布偏差。因此,本文以最大均值差异度量(maximum mean discrepancy metric,MMDM)从全局角度最小化中间域和目标域间的分布差异,DGT和DT的MMDM(DGT,DT)为
(4)
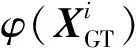
(5)
式中,1表示全1向量。投影后的中间域为ΦTφ(X)T·φ(XS)Z。因此,MMDM为
(6)
1.3 低秩约束正则化
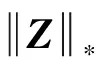
(7)
1.4 流形特征域适配
通过以上分析,流形特征域适配共包含局部生成差异度量、最大均值差异度量和低秩约束正则化三项。结合式(3)、(6)和(7)流形特征域适配的目标函数为
(8)
式中,τ和λ1为折衷系数。为防止出现平凡解,令PTP=ΦTKΦ=I。
本文在流形特征域适配的基础上通过变量交替优化的策略获取最优传输矩阵Z和投影矩阵P,利用特征值分解方法求解变量Φ,采用非精确增广拉格朗日乘子(inexact augmented Lagrange multiplier,IALM)[18]和随机梯度下降方法求解变量Z。因此,式(8)可表示为
(9)
式中:J为辅助变量;1为全1矩阵;R1为滞后乘数;μ为惩罚参数。参数求解如下。
1.4.1 求解参数Φ
固定变量J和Z,对式(9)进行重构,通过特征值分解,获取第k次迭代的解Φk,计算过程中将Φk(:,i)设为零,即:
(10)
式中,Φk(:,i)为Φk中第i个最小特征值的最小特征向量。
1.4.2 求解辅助变量J
固定参数Z和Φ。去除式(9)中与J无关的项,通过K+1次迭代后得到JK+1
(11)
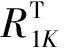
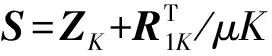
1.4.3 求解传输矩阵Z
固定变量J和Φ,对(9)进行重构,去除与Z无关的部分,利用梯度下降算子求解Z,获取最优值。第K+1迭代的解ZK+1为
ZK+1=ZK-α·∇(Z)
(12)
式中:∇(Z)为梯度;α为梯度下降系数。具体求解过程如下
(13)
本文所提方法主要是对相关变量J,Z和Φ的迭代优化,其求解需要输入源域数据XS和目标域数据XT,折衷系数τ和λ1。具体步骤如下:
步骤1输入源域数据XS和目标域数据XT,折衷系数τ和λ1。
步骤2根据式(3)在再生核希尔伯特空间中计算KT=φ(X)Tφ(XT),KS=φ(X)Tφ(XS),K=φ(X)Tφ(X),X=[XS,XT]。
步骤3初始化变量J和Z,即J=Z=0。
步骤4固定Z根据式(10)使用特征值分解方法求解Φ。
步骤5步骤五固定Φ使用IALM求解Z。固定Z,根据式(11)更新优化J;固定J,根据式(13)求解优化参数Z。
步骤6求解滞后乘数R1:R1=R1+μ(Z-J)。
步骤7求解惩罚参数μ:μ=min(μ×1.01,maxμ)。
步骤8检查收敛性,输出变量Z和Φ。
2 基于流形特征域适配的滚动轴承故障诊断
基于流形特征域适配的滚动轴承故障诊断方法包含以下四部分:数据采集、特征提取、流形特征域适配、故障识别:
(1) 采集不同工况下滚动轴承振动信号;
(2) 通过数据预处理提取样本29维时域和频域特征,构建源域训练样本集和目标域测试样本集,其详细公式见文献[20-21];
(3) 根据式(8)构建流形特征域适配模型,迭代优化变量Φ,Z和J,输出Φ,Z;
(4) 在子空间中通过投影矩阵和传输矩阵获取中间域和新的目标域;
(5) 迭代更新数据伪标签,然后利用最小二乘法进行分类,获取最终诊断结果。
所提故障诊断方法流程如图2所示。
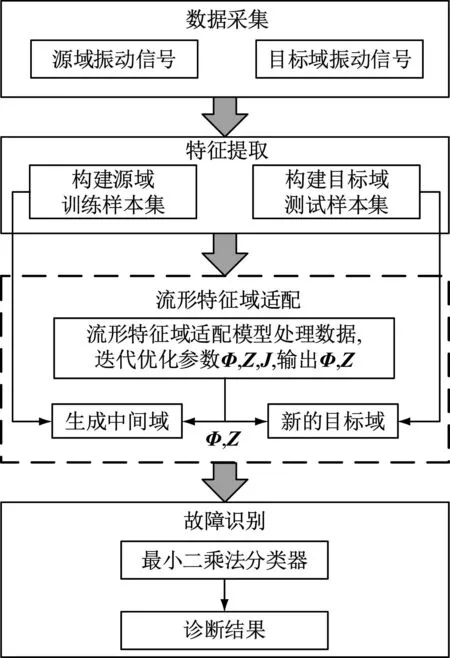
图2 故障诊断流程图
3 试验和分析
3.1 试验数据
为了验证所提方法的有效性,对同一设备下的跨域故障诊断试验进行分析,数据来源于课题组滚动轴承振动测试台,如图3所示。试验轴承为NSK 6205,包括5种滚动轴承运行状态:正常、内圈故障和外圈故障(故障直径:0.2 mm、0.5 mm)。在转速为1 800 r/min和2 400 r/min中采集不同径向载荷(0、600 N)下每种轴承的振动信号,采样频率10 240 Hz。数据集中每类工况包含100个样本、样本长度为1 024点。

图3 滚动轴承试验台
根据负载和转速不同设置4种不同工况,分别标记为A、B、C、D,具体信息如表1所示。此外,为验证模型在复杂工况下的泛化性能,设置单域迁移(源域和目标域为单一工况)和多域迁移(源域和目标域中具有多工况)试验对模型性能进行验证。单域迁移试验中,源域和目标域数据集每类100个共500样本;多域迁移试验中,AB、BC等每类100个共1 000个样本,ABC等每类100个共1 500个样本。
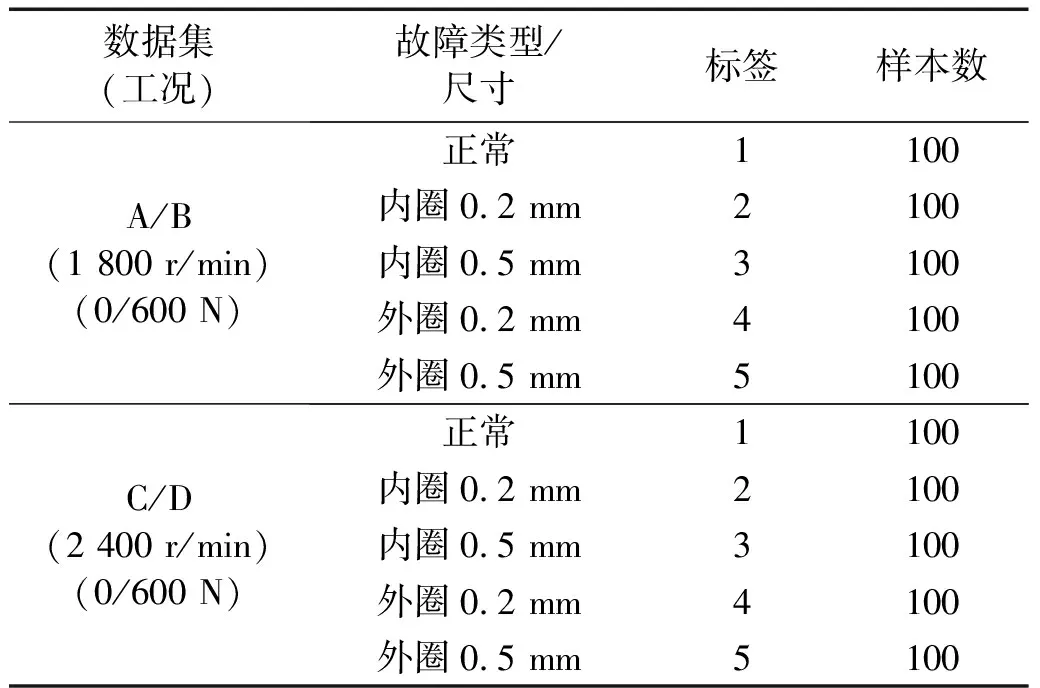
表1 滚动轴承数据集
3.2 参数设置
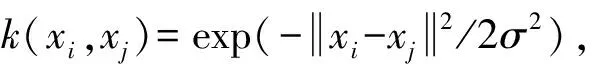
3.3 试验结果分析
同一设备下7种方法的跨域故障识别结果如表2、3所示。由表2可知,在单域迁移中,所提方法的平均识别率达到98.21%。由表3可知,在特征分布复杂的多域中,所提方法的平均识别率可达96.69%。随着工况复杂程度的提高,本文方法诊断精度仍高于KNN,SVM和其他五种迁移学习方法。原因在于:机器学习方法直接基于原始数据训练模型进行测试,泛化效果差,分类能力低。迁移学习方法中,GFK经过特征选择与变换,减小了数据差异,但未进行域分布对齐,出现过适配,影响了分类效率;TCA和SSTCA直接对数据进行分布对齐,导致分布不一致的数据间出现特征扭曲,诊断精度下降;TLPP基于相关假设构建数据先验结构,传递相关信息,最小化域间分布差异,但特征发散未解决,不利于样本区分;DANN仅考虑源域和目标域之间的相似特征,在数据中难以保证特征空间的对齐。本文方法在域分布对齐前以源域生成和目标域具有相似分布的中间域,从局部角度保留数据间的深层判别性信息,避免了特征扭曲,减小了数据间的偏移。
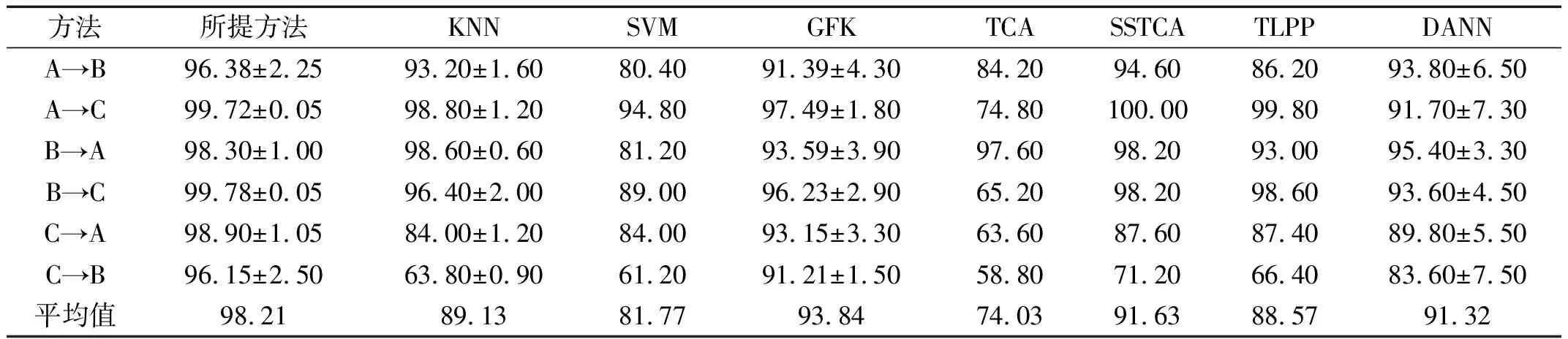
表2 单域不同算法对比结果
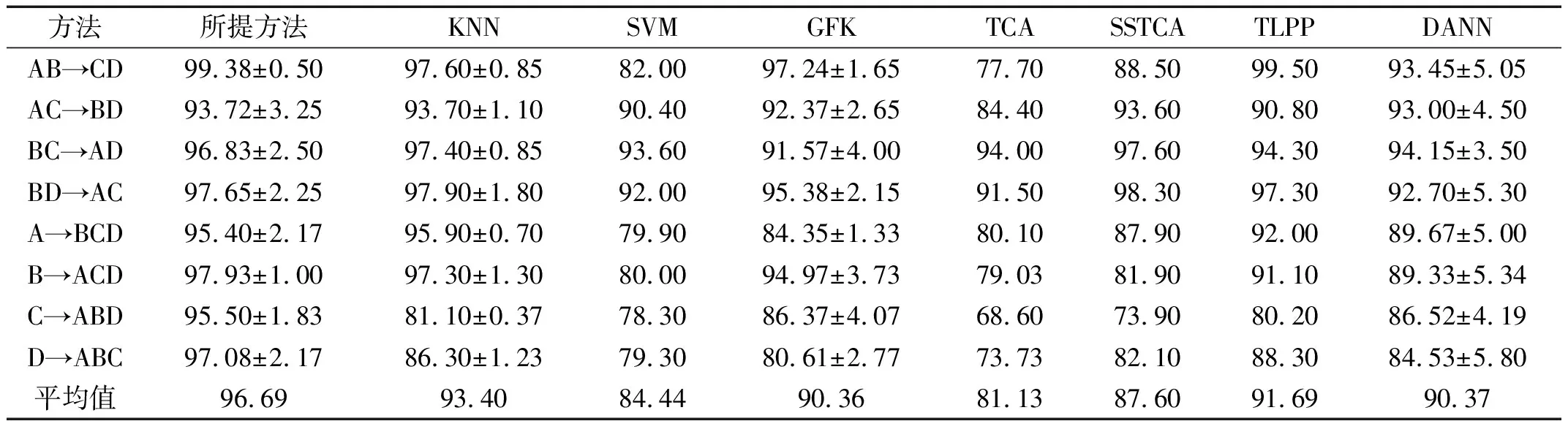
表3 多域不同算法对比结果
为了深入探究本文所提方法和相关对比方法的工作机制,随机选取迁移任务BC→AD,利用t-分布邻域嵌入(t-distribution stochastic neighbor embedding,t-SNE)算法对各迁移学习方法进行特征可视化,并以散点图呈现,如图4所示。由图4可知,几种迁移学习方法经域适配后,大部分故障类别区分较明显,但同类故障聚合性差,且正常和外圈0.5 mm样本重叠,故障难以区分。由图4(f)可知,所提方法的样本聚类效果明显,数据可分性更强。原因在于:本文所提方法通过域生成和分布对齐,以中间域将源域和目标域对齐,增强了领域间相似性、判别性信息,降低了差异性信息对故障识别结果的影响,使故障特征可分性和代表性更高。
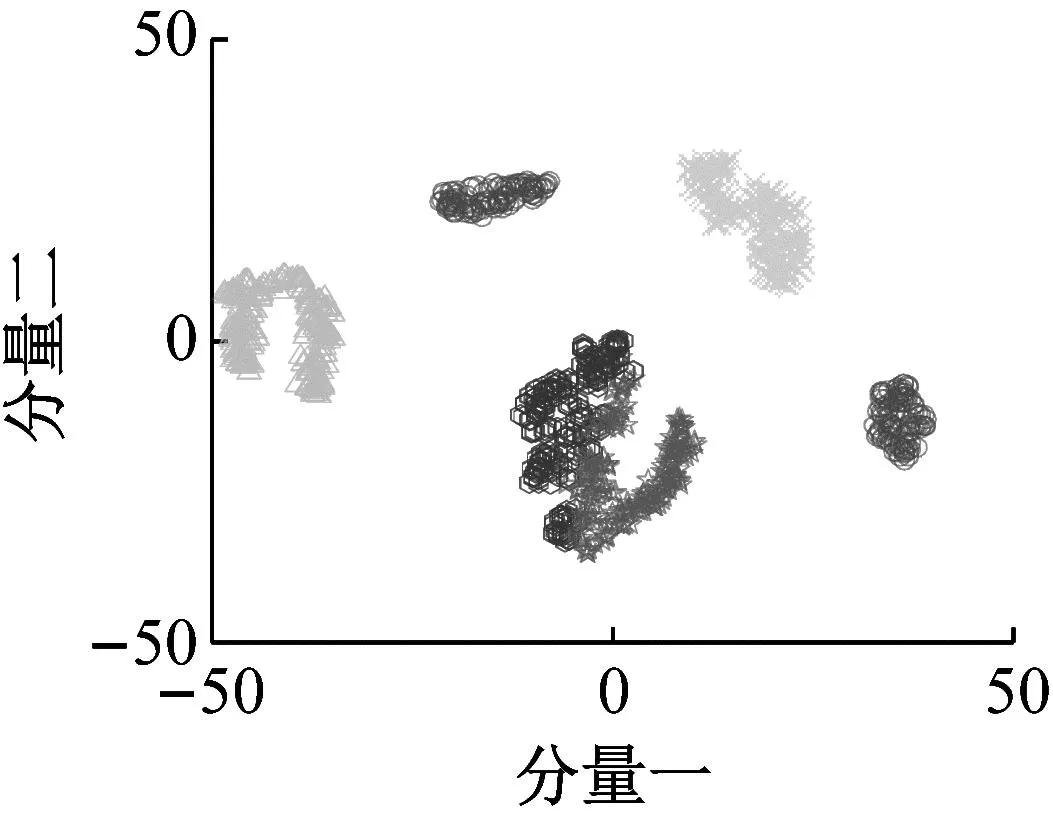
(a) GFK
同时,为了验证域生成和分布对齐的有效性,如图5所示,以B→ACD任务为例,对比了不同方法在不同样本数量下的准确率。其中,源域数据集中每类故障样本量由15递增至100,目标域数据集中每类故障样本量为100。由图可知,所有方法的诊断性能均随着样本数的增加而有所提高。此外,所提方法在样本数为35时便可以达到稳定状态,其他方法的准确率虽随着样本数增加而呈现上升趋势,但诊断性能均低于所提方法。原因在于本文方法可避免源域和目标域之间的转换误差以提高模型的泛化能力。
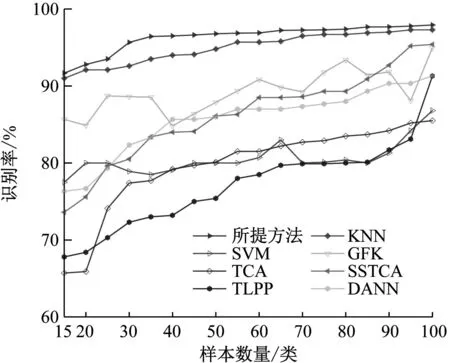
图5 不同方法的准确率对比
3.4 参数分析
高斯核参数的影响着中间域的生成,进而影响故障诊断效果,因此有必要对的敏感性进行讨论。随机挑选4个迁移任务(A→B;C→B;A→BCD;AC→BD)在不同高斯核σ参数下进行试验,结果如图6所示。由图6可知,各任务的识别准确率随的增大呈下降趋势,其识别精度在[0,1]范围内虽有波动,但整体拥有较高水平。对于其他参数,本文通过遍历寻优获取最优参数组合以提高模型的性能。
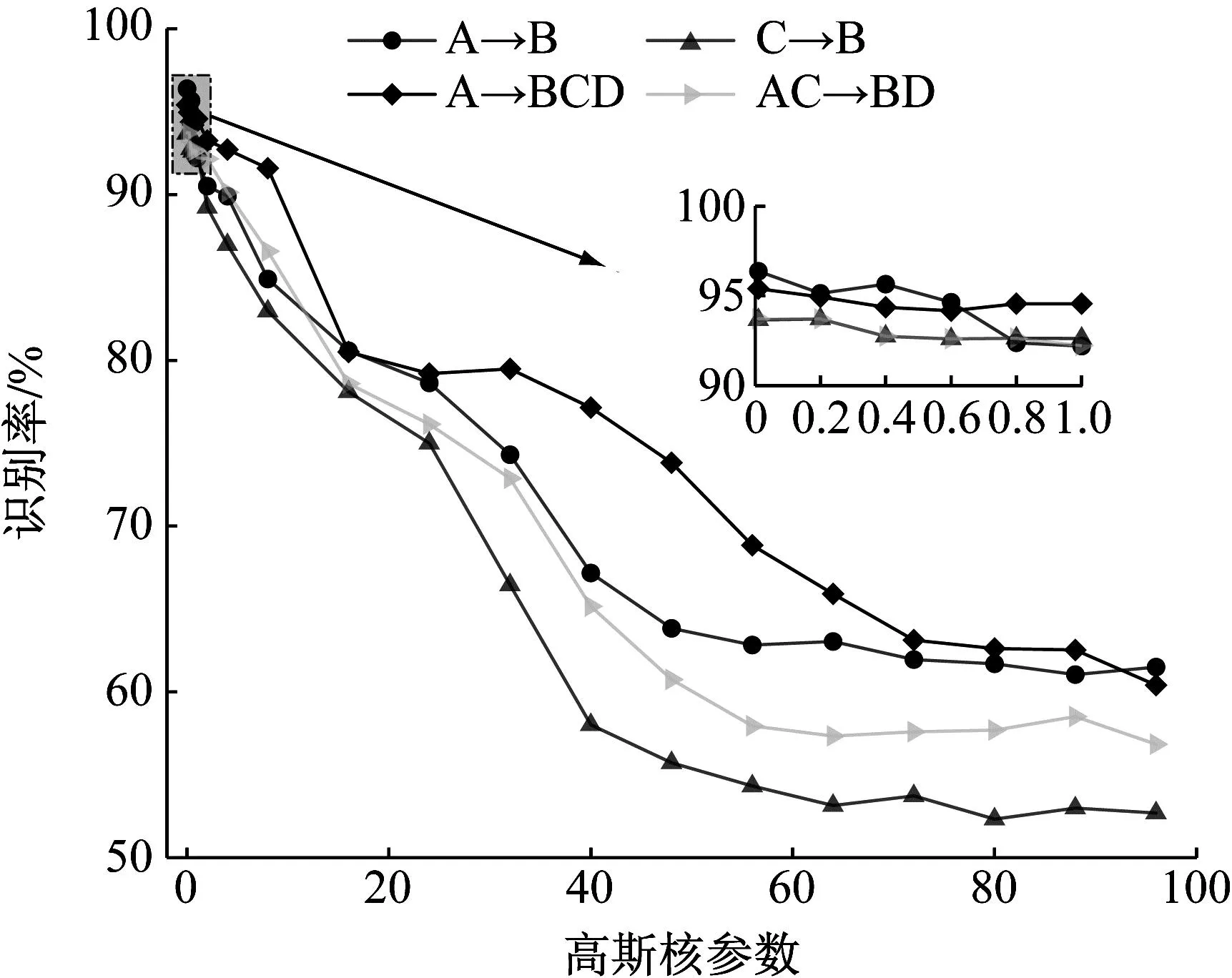
图6 高斯核σ参数敏感性
3.5 计算效率分析
为了进一步分析所提方法计算效率,随机挑选2个迁移任务(C→A;BD→AC)对所提方法、GFK、TCA、SSTCA与TLPP的时间复杂度进行讨论。结果如图7所示。各任务的计算时间随样本数增加而增加,但所提方法的计算时间除GFK外均少于其他方法,原因在于GFK只处理数据局部域信息,大大加快与简化了计算过程,而本文所提方法在处理数据局部信息的同时,处理数据全局信息,导致计算复杂度增加,计算时间较长。
4 泛化性能试验
4.1 试验数据构建
为了分析所提方法的泛化性能,将其应用于不同设备下的跨域故障识别。试验研究对象为深沟球轴承。数据来源于凯斯西储大学轴承数据中心(Case Western Reserve University,CWRU)[27]、机械故障预防技术学会(MFPT)[28]和课题组滚动轴承试验台(ZC),数据集分别以E、F和G表示,每个数据集选取正常(N)、内圈故障(IR)和外圈故障(OR)三种类型,每类以1 024个样本点截取100个样本,具体信息如表4所示。设置多域迁移试验方案,其中E、F、G各300个样本,EF、FG、EG各600个样本,EFG各900个样本。
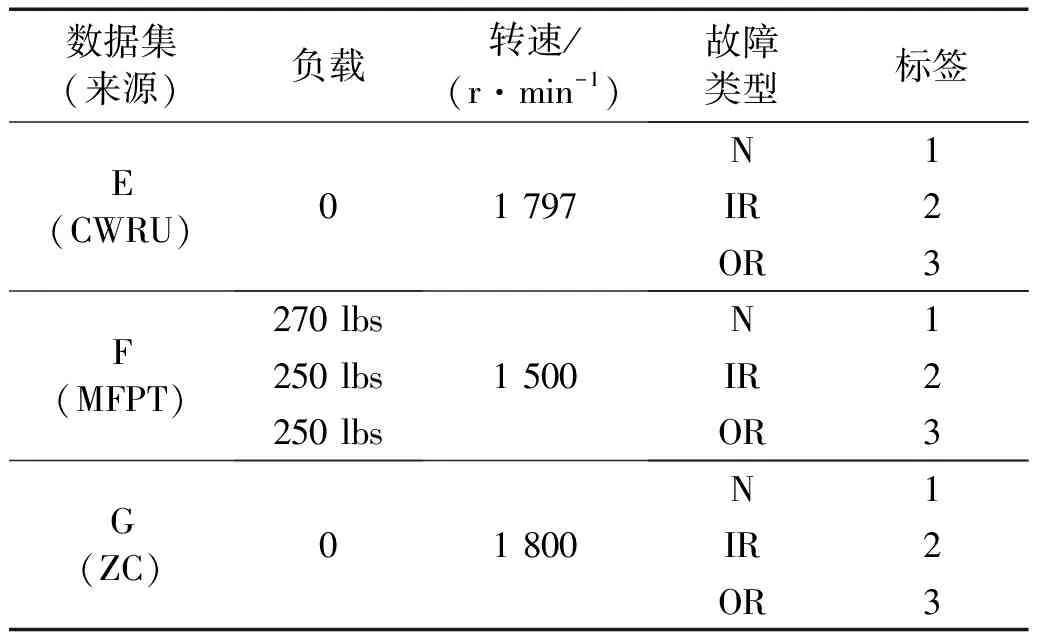
表4 轴承工况信息
4.2 试验结果分析
表5和图8分别为跨域诊断结果和G→EFG t-SNE图。由结果可知,所提方法在不同设备下的跨域故障识别的平均识别率可达99.86%。GFK虽然在子空间中通过特征选择与变换可获取明显分类效果,但未进行域分布对齐,导致GFK较所提方法低4.01%。面对数据分布差异更大时,TCA和SSTCA仅考虑边缘分布对齐,数据之间偏移更大,特征扭曲更为严重,导致所提方法平均识别准确率较TCA高12.06%,较SSTCA高11.30%。TLPP虽然基于相关假设构建数据先验结构,最小化域间分布差异,传递相关信息,但未考虑类内和类间距离,不利于样本区分,使得所提方法识别准确率较TLPP高11.77%。DANN虽然具有较强的自适应能力,但在不同设备下,域间数据差异大,其诊断性能大幅度下降,导致DANN较所提方法低9.46%。对比图8,面对数据分布差异复杂时,所提方法通过域适配和域生成减小域间差异,并保留局部几何结构中的判别性信息,提高了数据类内紧密性和类间可分性。
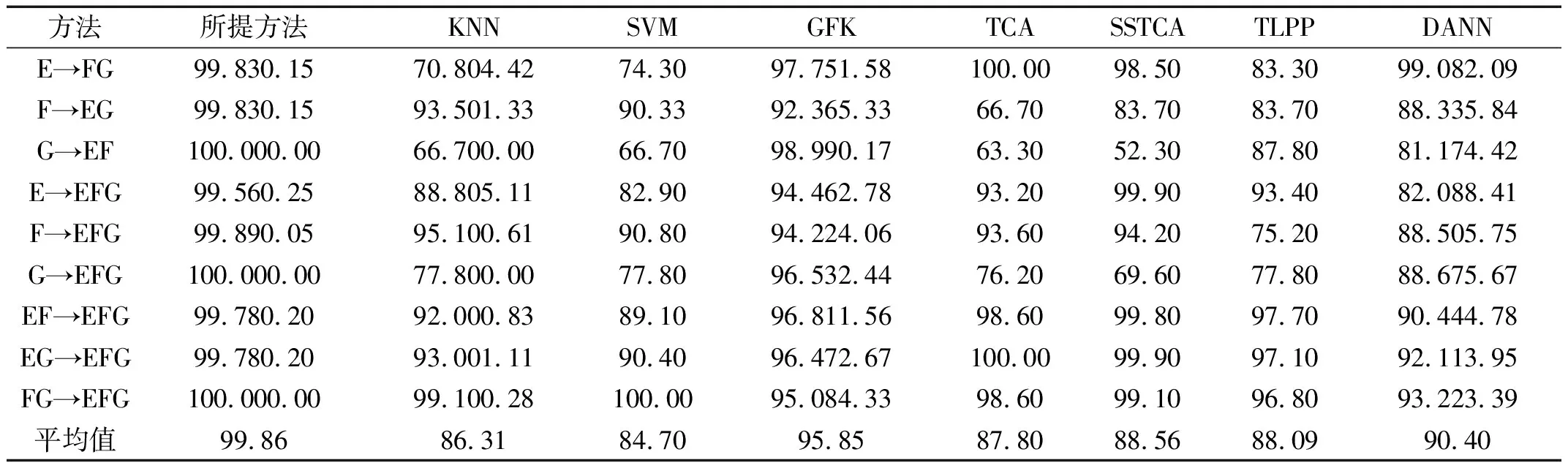
表5 跨域诊断结果
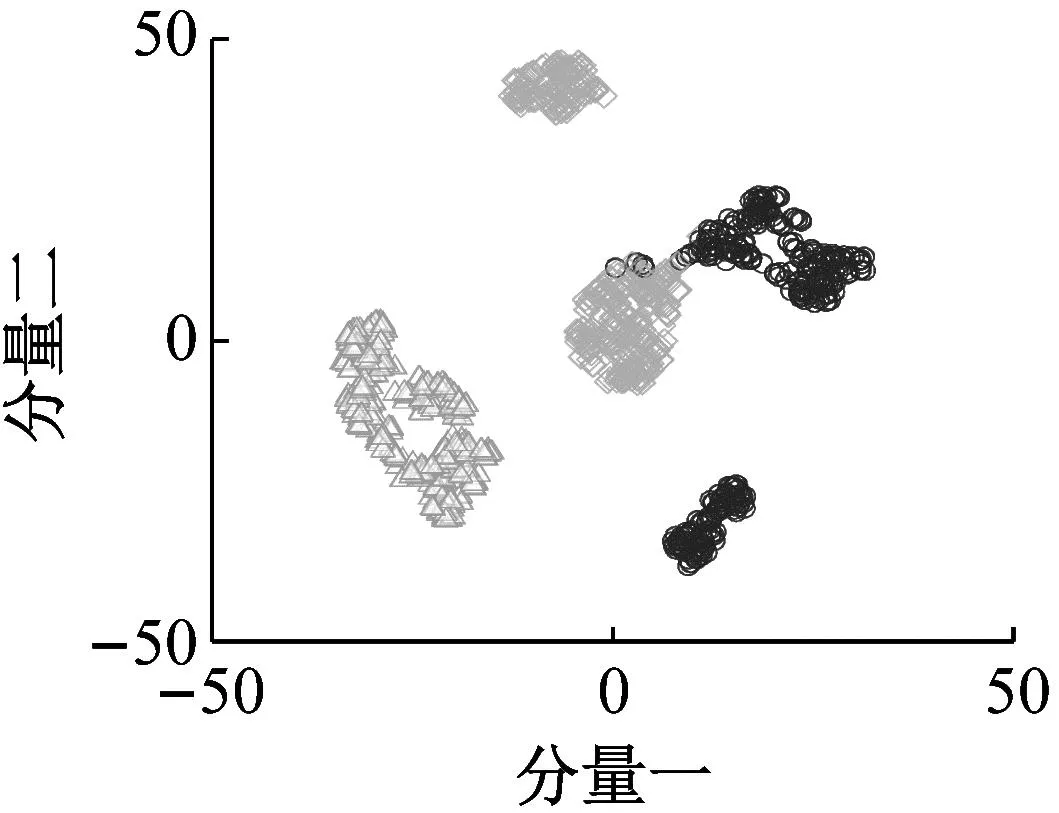
(a) GFK
5 结 论
在本文中运用MFDA对跨工况下滚动轴承进行故障识别,旨在解决多工况下复杂分布数据在原始空间进行分布对齐时,出现的特征扭曲和发散问题。优势在于:
(1) 利用源域数据以无监督的方式生成一个与目标域具有相似分布的中间域,并利用局部生成差异度量保留数据流形局部几何结构中潜在的判别性信息,不仅能够避免数据扭曲与发散,还能够从局部角度提高源域与目标域之间的分布一致性。
(2) 通过最大均值差异度量对数据进一步对齐,从全局角度最小化数据间的分布差异,在面对多工况下产生的复杂分布差异时仍能取得很好的效果。
(3) 基于MFDA框架建立的故障识别模型诊断能力强,经过单域和多域试验验证了所提方法具有优良的鲁棒性、泛化性能和工程实际应用价值。

