桥梁抗风型TMD对车-桥耦合振动系统减振性能研究
刘修平,王 涛,杨克焕,冯 宇,韩万水
(1.长安大学 公路学院,西安 710064; 2.广东华路交通科技有限公司,广东 广州 510000)
调谐质量阻尼器(tuned mass damper,TMD)是一种最为常用的被动控制系统。它是在结构物的上部或下部的某一位置上加上惯性质量,配合弹簧和阻尼器与主体结构相连接,通过调节其自振频率与结构振动的某些振型频率相一致,利用共振原理“吸振”的一种装置。其构造简单,安装方便,易于后期维修养护,而且不依赖其余的外荷载激励,这些优点都是其他控制方式无法比拟的,因此,在高层建筑、桥梁等结构的振动控制领域得到重视[1-3]。
目前,TMD系统在桥梁中的应用主要是来解决涡激共振、风致抖振以及地震等外界激励荷载导致结构振幅过大的问题,并取得了良好的效果[4-5]。王志诚等[6]基于谐响应和时程分析研究了崇启大桥的低频TMD系统的设计方法和减振效果,为类似工程的涡激共振振幅控制提供了参考;文永奎等[7]研究了斜拉桥多阶模态参与的分布式TMD系统的优化设计参数,通过风致抖振分析检验了其有效性;向越等[8]设计了黏滞阻尼与滞变阻尼同步作用的双阻尼新型TMD,并将其应用于地震激励的响应减振分析中,得到了良好的减振效果;不同于风和地震荷载引发的强动力效应,车致振动虽然不会影响到桥梁整体结构的安全性,但随着桥梁结构形式的多样化、桥面宽度、车辆速度和载重的不断加大,由于路面或轨道的不平顺,高速运行下的车辆对桥梁的往复性地冲击作用也会导致桥梁构件的疲劳问题,缩短桥梁的使用寿命[9]。张新亚等[10]将TMD系统应用于高架轨道桥梁结构振动及振动噪声问题的研究,并建立了列车荷载-轨道箱梁-TMD耦合动力分析系统,分析了不同频段的结构振动加速度和减噪控制效果。刘广波等[11]研究了适用于高速列车-桥梁减振的MTMD的选取方法和最优布置方案,并分析了引入TMD系统后对高速铁路桥的扭转性能改善的情况;王浩等[12]通过变化TMD的刚度和阻尼的取值,研究了安装TMD对列车在不同运行速度下引起的振动的控制效果。
受TMD质量、振动行程要求和桥梁安装空间的限制,常规公路桥梁梁体结构中安装TMD的工程案例并不多见,既有建成公路桥梁用TMD的初衷仍然以抑制风致涡振为主,基于桥梁抗风型TMD工程实例开展其对汽车-桥梁耦合振动系统的减振研究相对较少。由于公路汽车的车型、车重、车速等信息差异性大,荷载随机分布性强,使得车-桥-TMD之间相互作用机理的复杂性和不确定性不断增加[13]。同时,传统TMD设计方法在获取多自由度被控结构模态质量方面的过程较为繁琐。因此,本文首先结合有限元模型动力计算特点,提出了模态动能演化的多自由TMD简化设计方法,引入Combin14弹簧单元建立了汽车-桥梁-TMD耦合系统,以经典质量弹簧案例分析了安装TMD后对车-桥系统动力响应的影响,并进行了参数敏感性分析,依托某大跨钢箱连续梁桥抗风型TMD工程实例,分析了车辆激励下的TMD减振性能。
1 多自由度结构的TMD控制方法
1.1 受控模态的选择与TMD布置
TMD系统由固体质量、弹簧、阻尼元件、导向系统和基座组成,是针对单个振动模态的一种被动控制方式,所以,在采用TMD系统进行振动控制前,需要先确定哪些振型参与了结构的振动。结构的振动行为通常可以视作是多个振型的组合,振型的参与情况通常采用振型参与系数衡量,一般而言,低阶振型的参与系数大,高阶振型的参与系数小。
对于桥梁结构,梁体振型函数φ(x)通常表达为
φ(x)=A1sinαx+A2cosαx+A3sinhαx+
A4coshαx
(1)
式中:x为沿着梁长方向的坐标;A1、A2、A3、A4和α为常数,可由梁振动的初始条件确定。
以简支等截面结构为例,其他大跨复杂桥梁与之类似,引入边界条件φ(0)=0、φ″(0)=0后,式(1)变为
(2)
式中:l为梁长;A1为常数,且不影响函数变化规律。
反映到振型上,得到简支结构的前三阶模态振型如图1所示。

(a)
根据固有振动的振型叠加原理,把式(2)中的A1归入Cn,那么,可进一步得到梁体任意时刻和位置的振动响应时变函数为
(3)
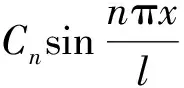
因此,在选用TMD作为振动控制时,其最优布设位置当选在所选模态振型的峰值处,以实现最大限度减振的目的。
1.2 动能演化的模态质量计算
多自由度结构TMD系统控制设计时,则需借助“等效关系”将多自由度结构转换成单自由度进行结构减振设计[14]。在结构离散后的j节点处引入TMD后,结构的振动方程可以表达为
(4)
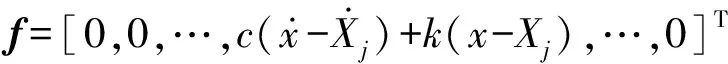
式(4)通过振型分解,可以推导出结构的第i阶振型对应的振动方程
k(x-Xj)]=Fi
(5)
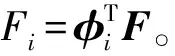
式(5)与单自由度被控结构-TMD系统的振动方程形式一致。只需将结构的质量、刚度和阻尼换成第i阶振型对应的模态量即可。
根据细长结构有限元模型动力计算分析的特点,采用集中质量法离散结构质量,那么,模态质量为
(6)
式中:Mi为第i阶模态质量;N为节点总数;mj为第j个节点的集中质量;Ixj、Iyj和Izj分别为第j个节点的x、y和z方向的转动惯量;uxij、uyij、uzij和rxij、ryij、rzij分别为x、y和z方向的平动和转动方向的归一化振型。
然而对于建立的有限元模型来说,用式(6)直接计算模态质量时,提取节点质量和节点振型的工序较为繁杂,为方便起见,可以改用提取动能的方式,利用推演的公式计算其模态质量。根据动能定理
E=0.5VTMV
(7)
引入单位矩阵I=ΦΦT,并将速度矩阵V用Φω代替,则式(7)可表达为
E=0.5(Φω)T·ΦMΦT·Φω
(8)
进而可以推导出
E=0.5ωTMω
(9)
式中:Φ表示模态振型;ω为模态的圆频率;M为模态质量矩阵。
那么,对于第i阶模态质量Mi,由动能公式推演到的求解方式如下
(10)
式中:Ei为第i阶模态主梁振动的动能,可在模态分析后直接提取得到;ωi为第i阶模态对应的频率。
1.3 设计参数的闭式表达[15]
在确定结构关键振型的模态质量后,可以通过质量比的概念对于TMD进行参数设计。Den Hartog给出的简谐荷载无阻尼振动情况下的TMD设计参数为
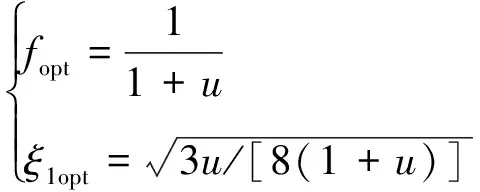
(11)
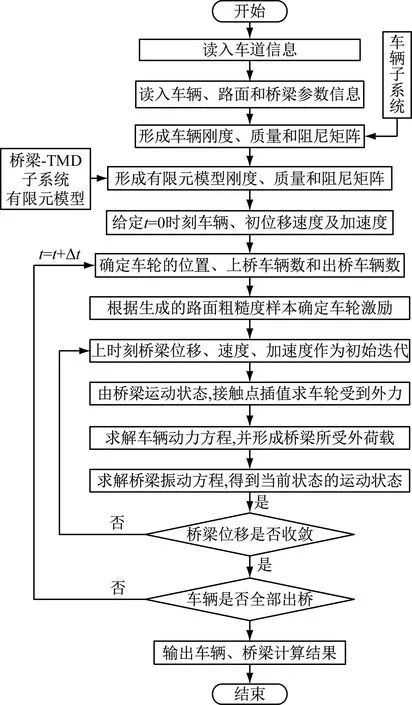
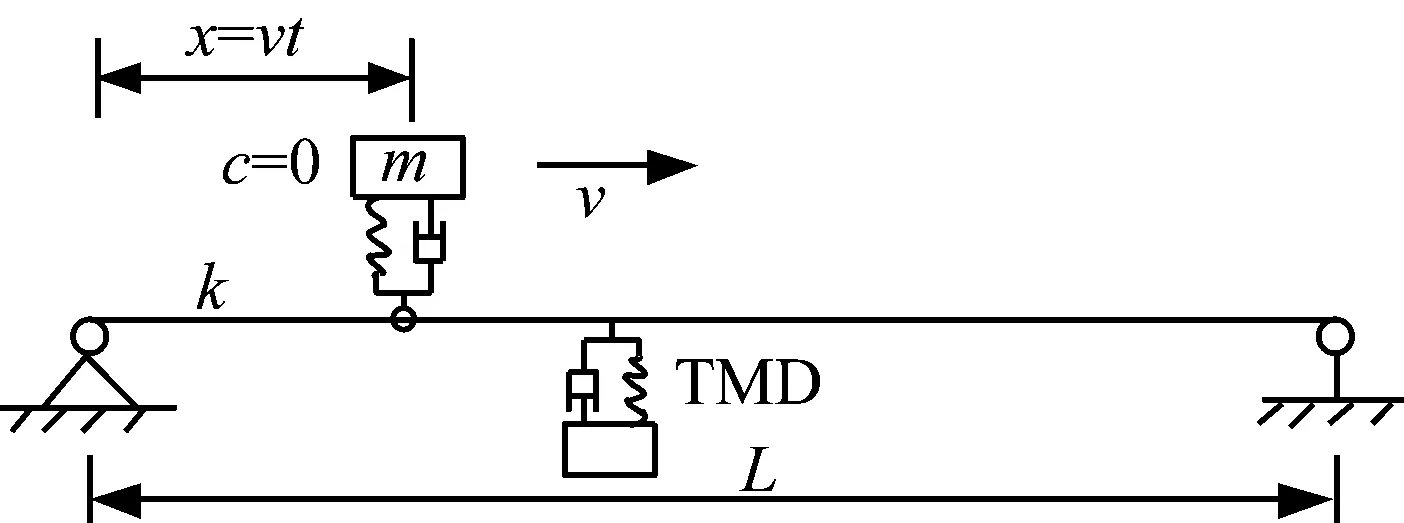
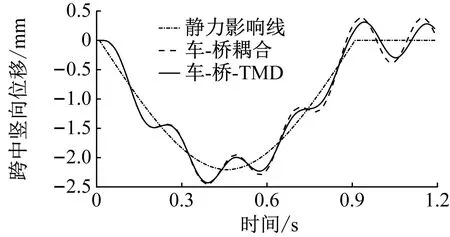
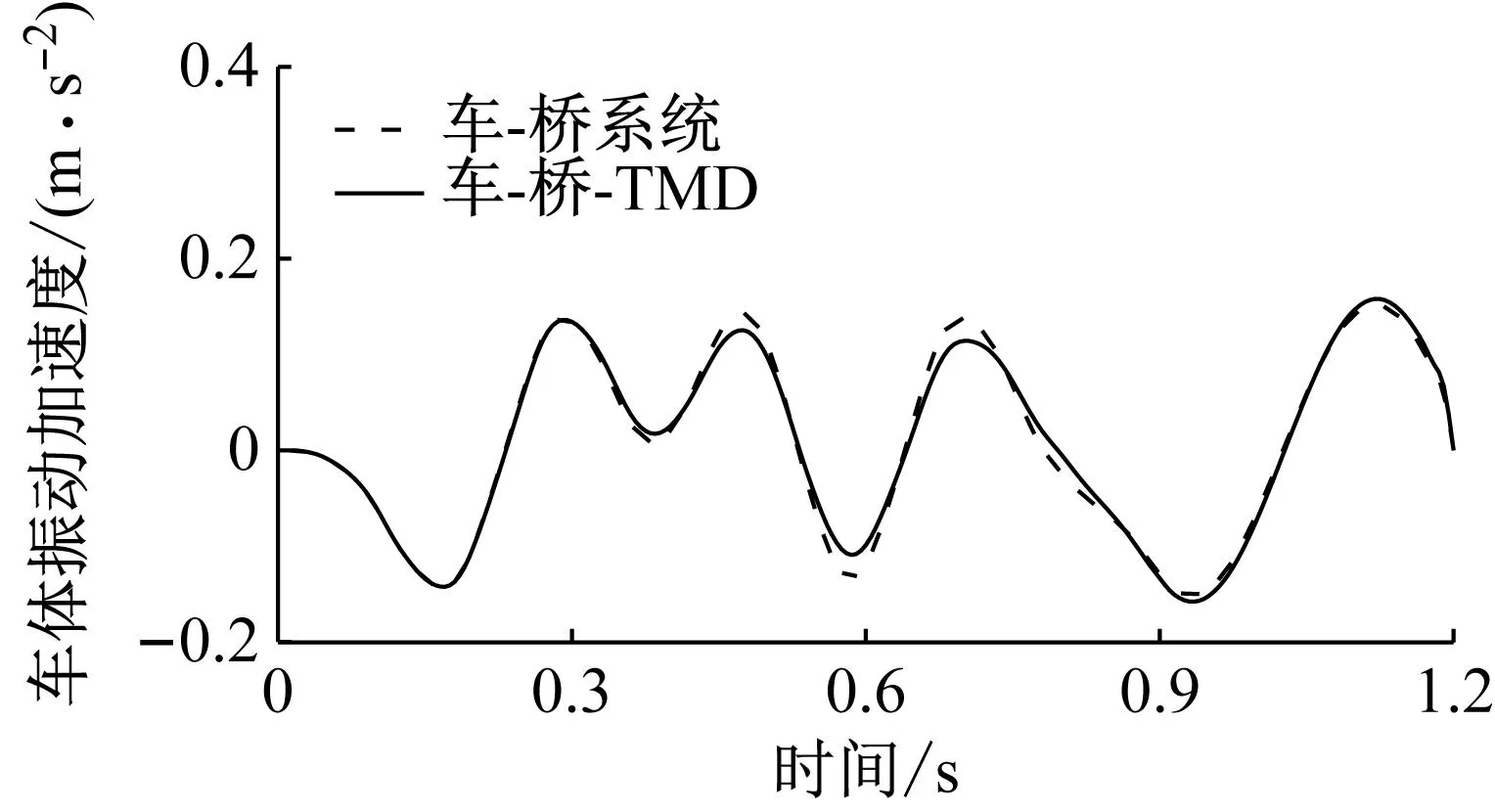
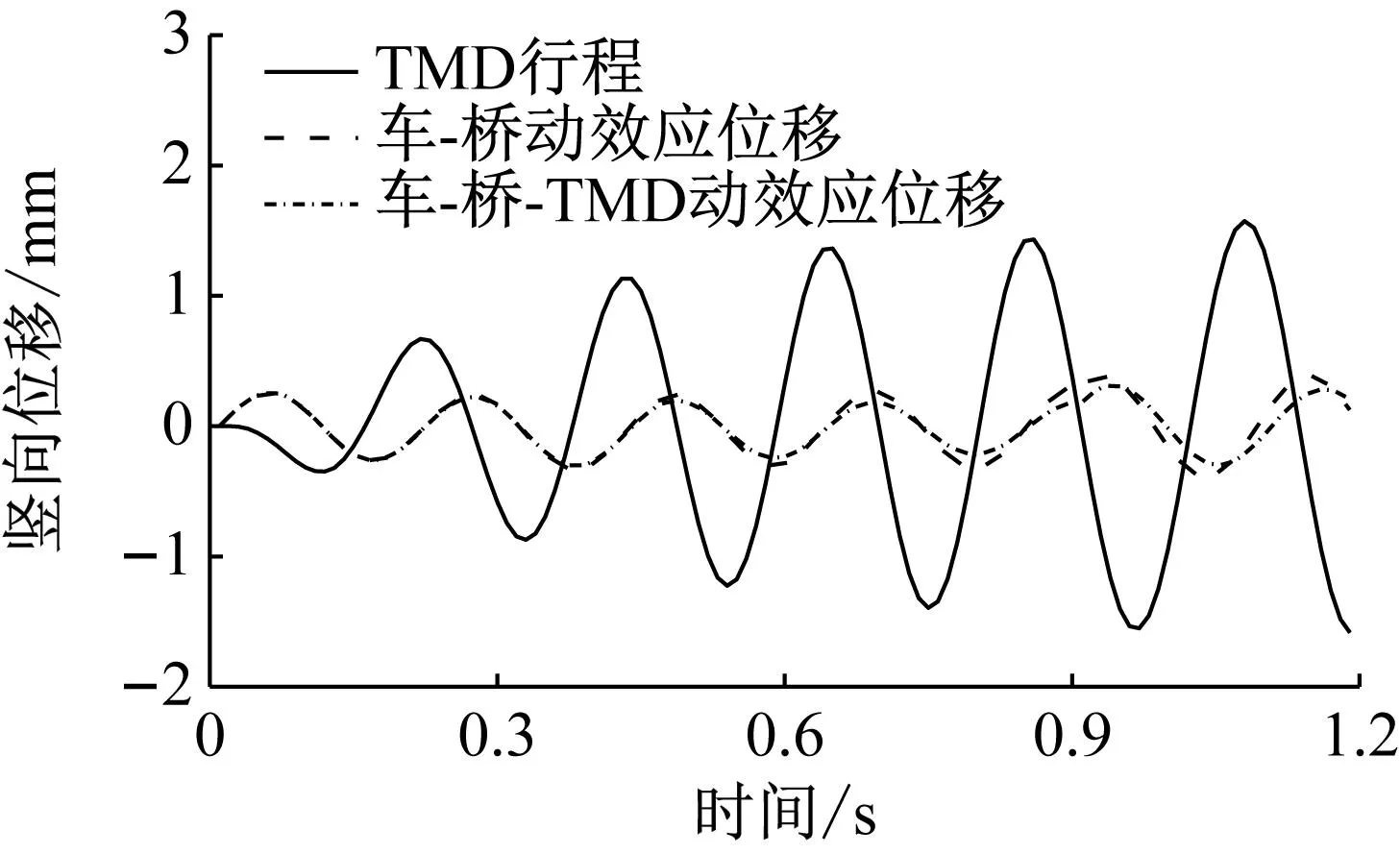
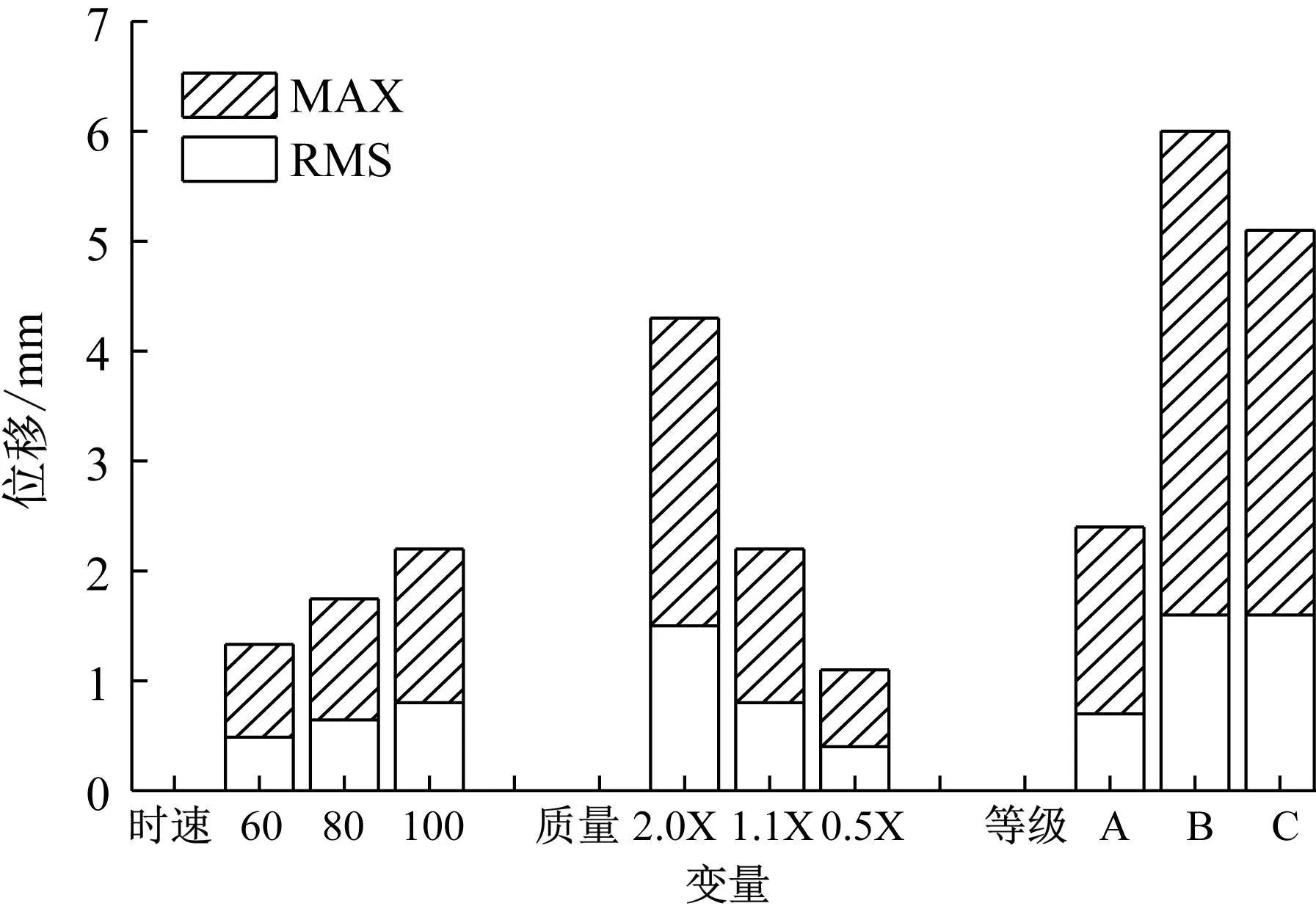
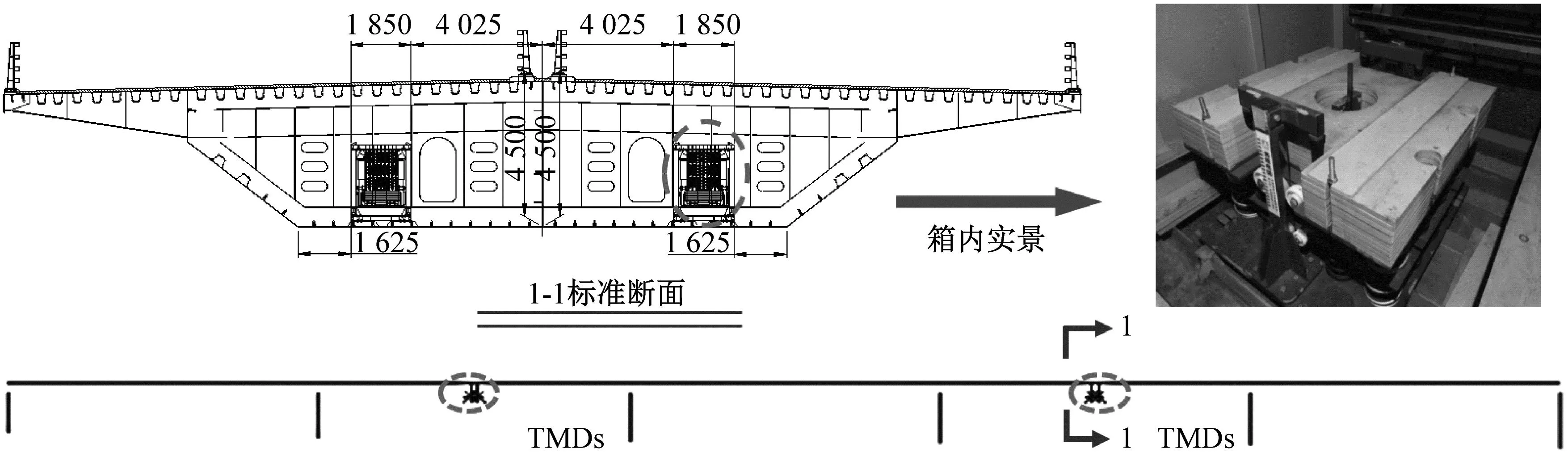
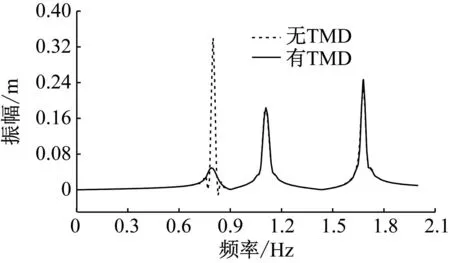
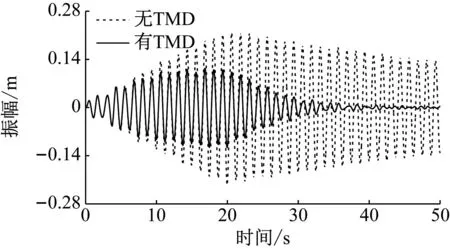
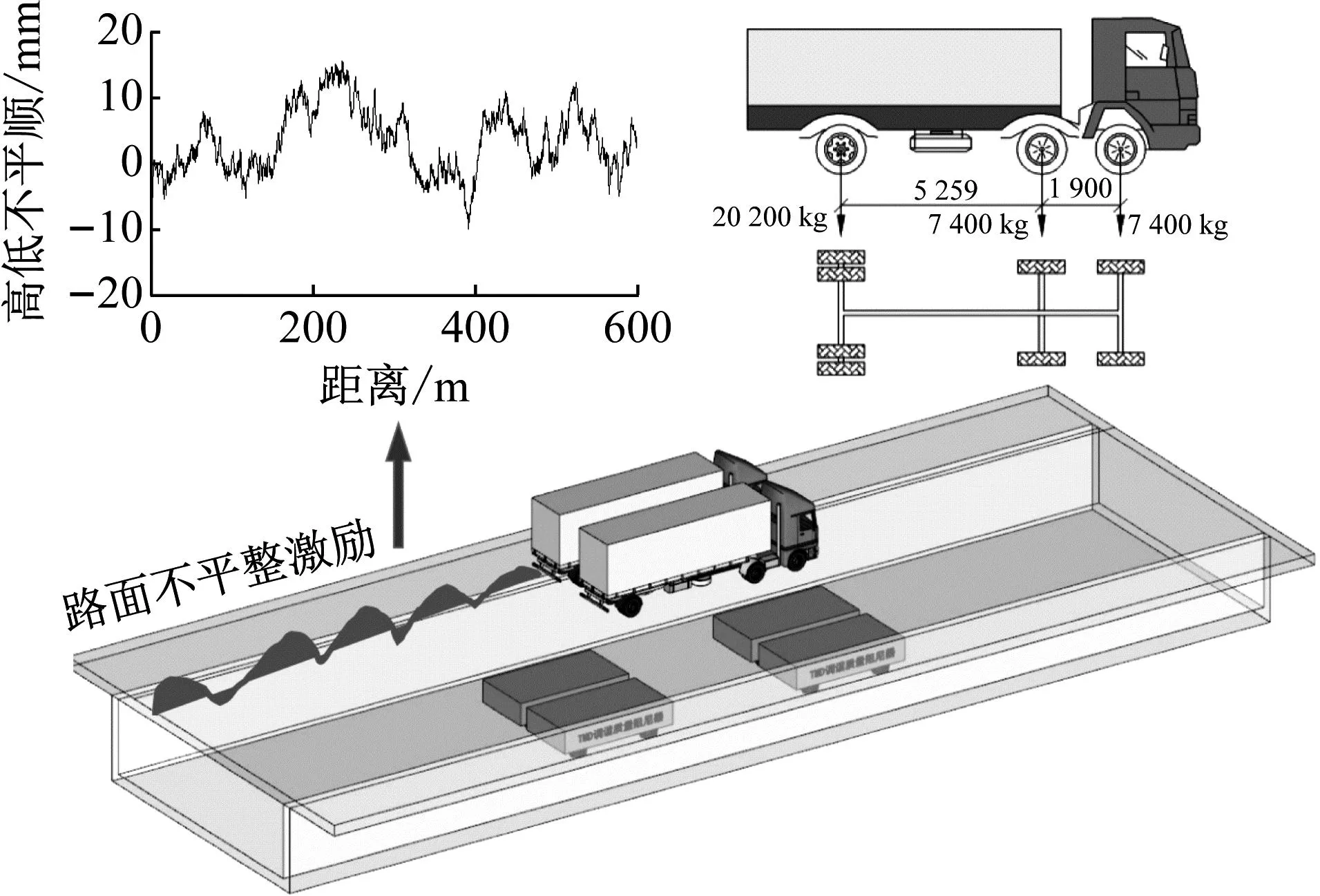
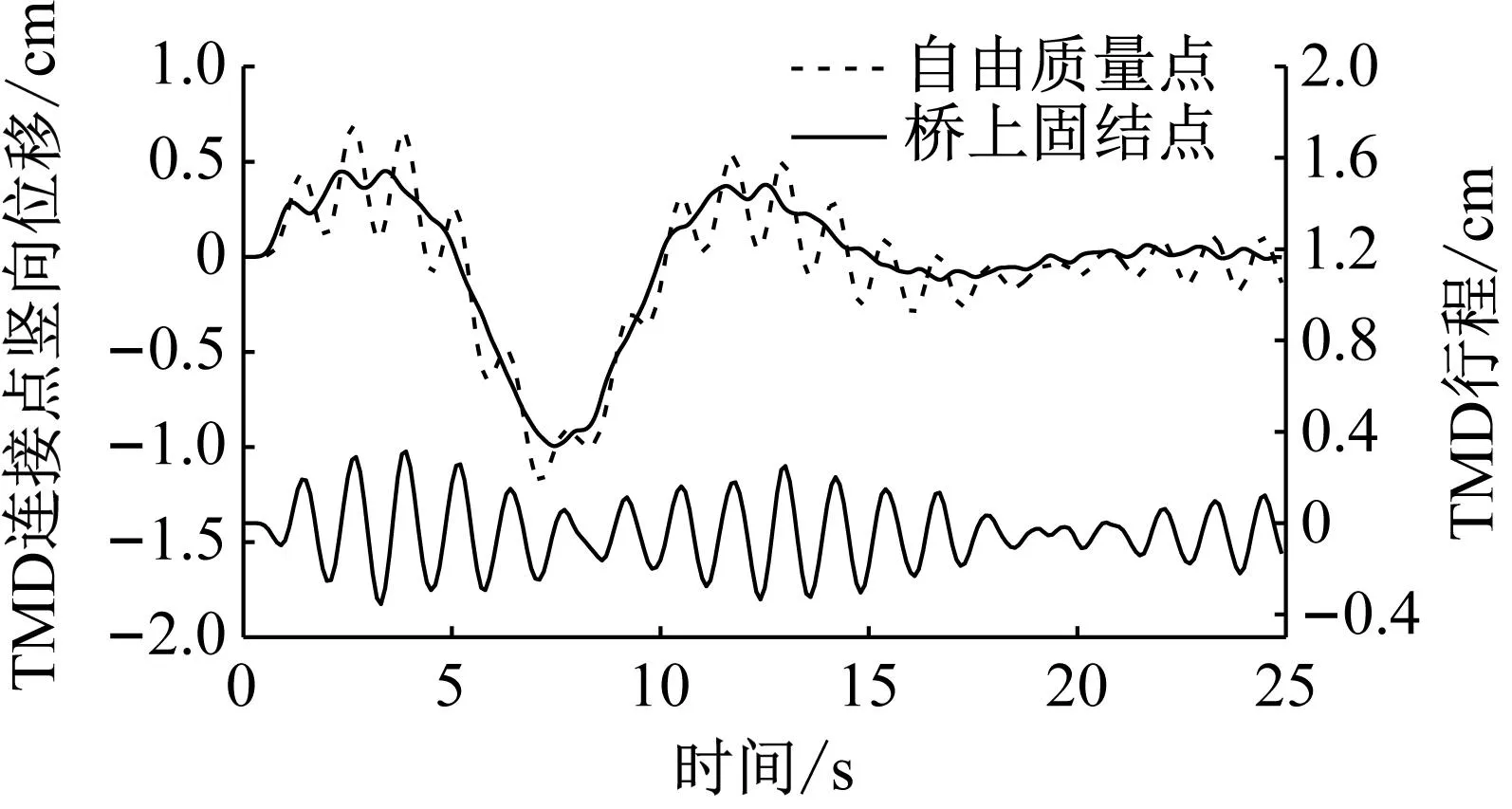
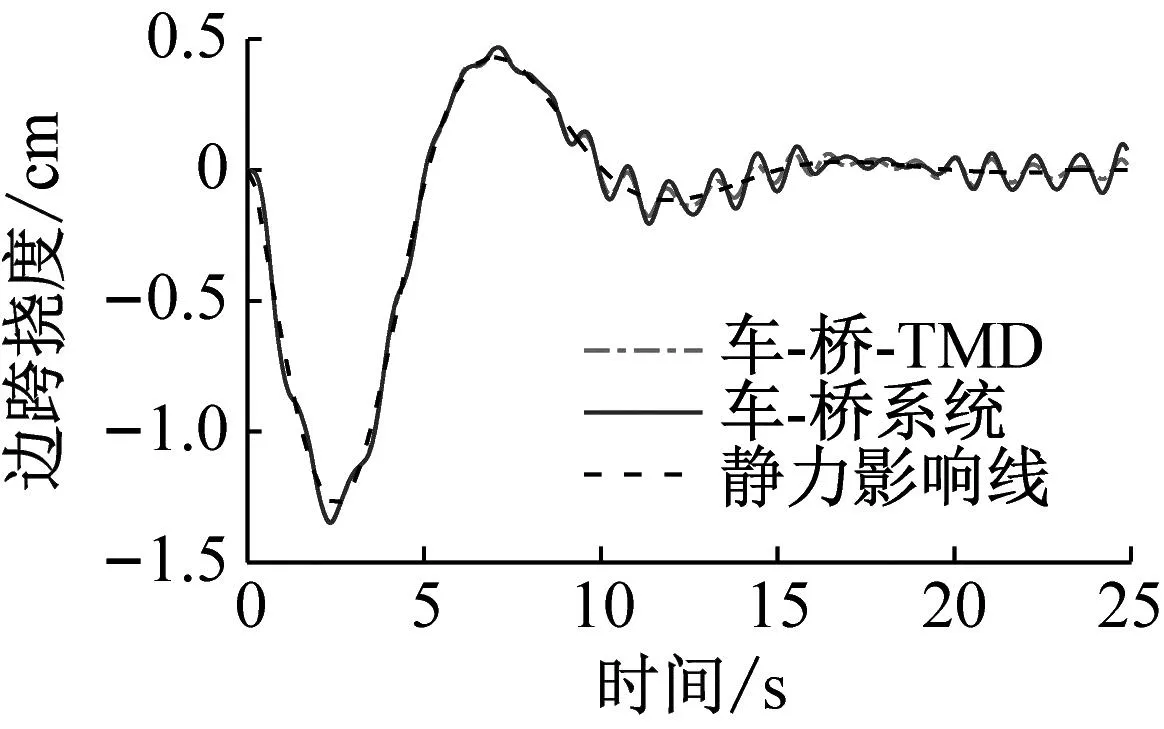
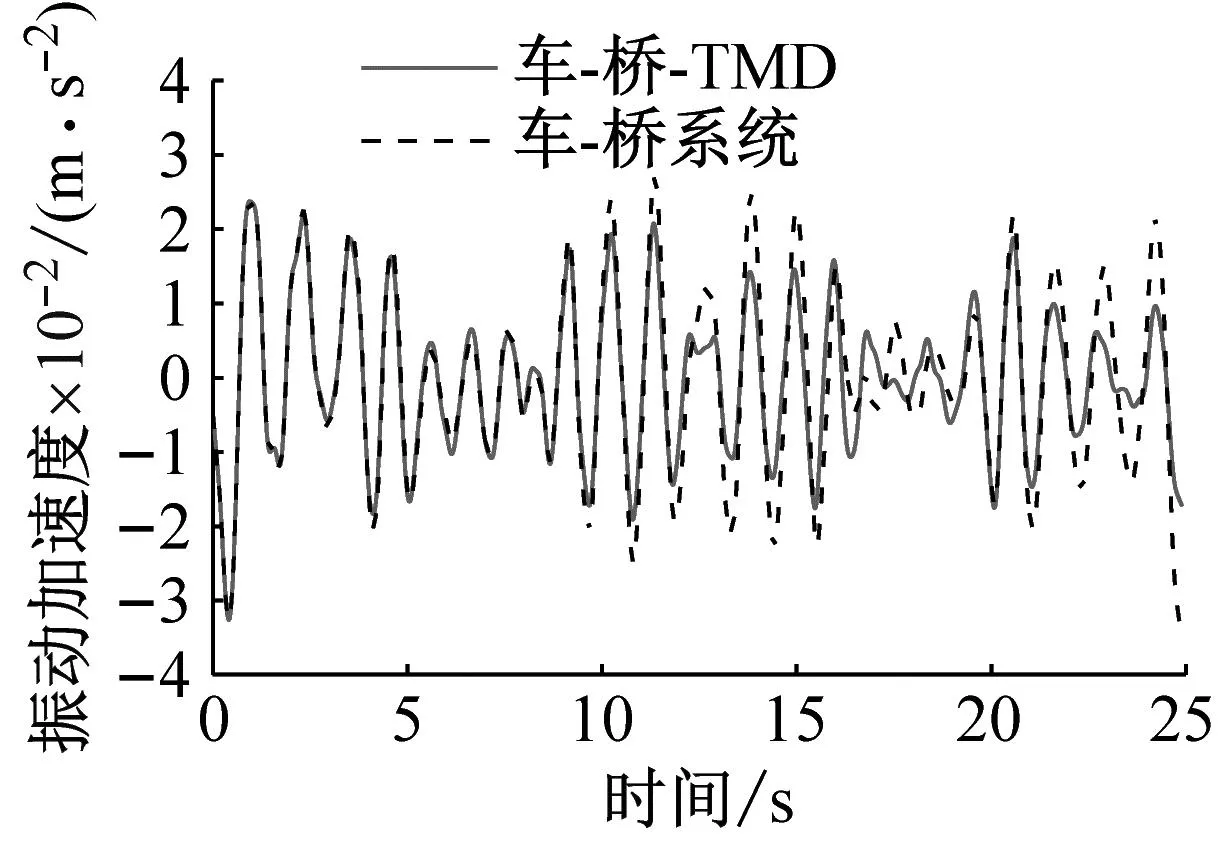
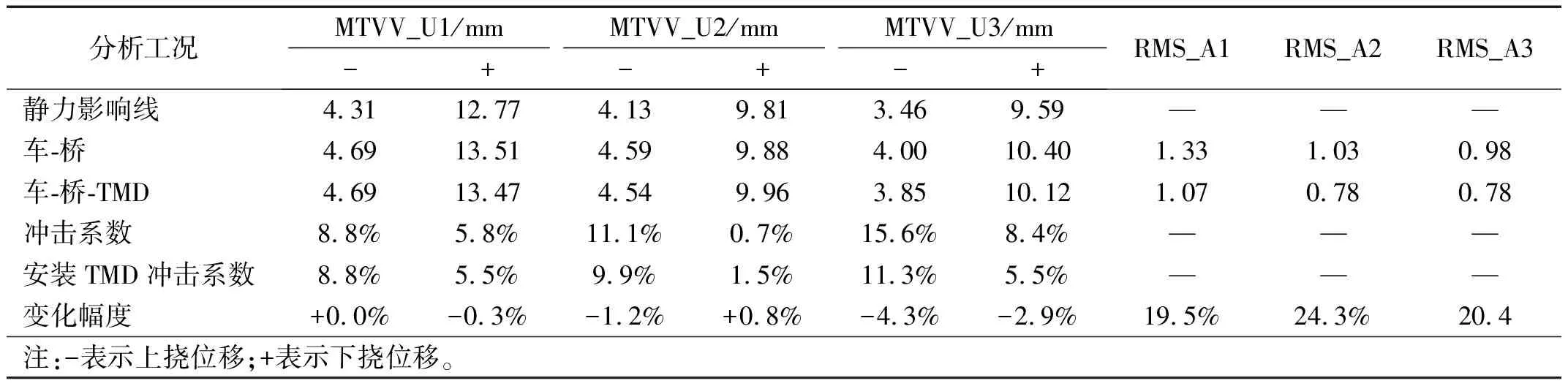
式中:u为TMD质量与结构模态质量的比值,一般0.5% Warburton给出了白噪声激励下的TMD设计参数为 (12) Den Hartog和Warburton的简化分析公式是解决桥梁TMD鲁棒性设计和优化的有效公式。在已有的工程实践应用中,更倾向使用Den Hartog公式。 在此基础上,进一步确定TMD的设计刚度kd和阻尼cd为 (13) 根据结构动力学理论,车桥耦合系统的动力方程可表示为[16] (14) 式中:M、K、C、Z、F分别为质量矩阵、刚度矩阵、阻尼矩阵、竖向位移以及车桥间作用力;下标v、b分别表示车辆和桥梁子系统。 当桥梁中有其他附属装置时,如TMD系统等时,需要更新桥梁的刚度、阻尼和质量矩阵,保持车辆系统与之分离。假设在桥梁的第i个自由度处设置TMD系统,按有限元直接刚度法,建立桥梁-TMD系统耦合振动方程为 (15) 在采用有限元方法进行结构分析时,TMD的弹簧、阻尼元件和导向系统可以采用弹簧单元模拟,Combine14支持弹簧刚度和阻尼的输入,具有平动和扭转两种属性,每个节点有3个自由度,在箱室内部,由于导向系统的限制作用,TMD系统只能沿着竖向方向运动,在模拟时只需开启平动属性中的竖向平动即可;固定质量则用质量单元Mass21来模拟,Mass21单元有3个转动和3个平动,共6个方向的自由度,这里由于导向系统的限制,只有平动特性,不考虑扭转质量;基座由于固定在箱梁顶或者底部,只需将Combine14的一端与箱梁位置处共节点即可,TMD实际的行程位移即为自由质量点位移与桥上固结点的位移之差,典型的TMD装置及采用的有限元分析单元形状如图2所示。 图2 TMD系统有限元模拟 为提升桥梁三维动力分析软件BDANS对TMD计算的兼容性[17],在有限元分析模型阶段中对照Combin14单元定义和参数赋值特点,按式(14)将其引入BDANS的桥梁有限元模型质量、刚度和阻尼组集模块,从而形成桥梁-TMD子系统。由于桥梁模型的自由度相对TMD数量差距很大,所以通过有限元直接刚度法集成的桥梁-TMD体系的计算效率与引入前相差并不大。考虑TMD的车-桥耦合振动系统时域求解流程如图3所示。 图3 车-桥-TMD系统计算流程 首先,根据已有信息分别建立汽车与桥梁-TMD两个子系统分析模块;其次分别建立汽车和桥梁-TMD各自的运动方程,并通过车轮与桥梁结构接触点处的位移协调条件和车桥之间的相互作用力的平衡关系,将两个子系统有机结合起来;将桥梁-TMD系统和车辆动力方程通过Newmark积分进行分离迭代计算,以桥梁位移是否收敛以及车辆是否全部出桥作为判断条件,满足判定条件后开始下一时刻的计算。满足计算设定时间步后,输出桥梁、车辆及TMD的时程计算结果。 以经典单自由度移动弹簧质量过简支梁模型为研究对象[18],如图4所示。分析车-桥-TMD耦合系统振动特性。其中,弹簧质量5.75 t,重力加速度取9.81 m/s2,竖向刚度1.595×106N/m,前进速度27.78 m/s,不考虑粗糙度的影响。 图4 经典质量弹簧计算模型 计算得到简支梁模型的前三阶竖向模态频率分别为4.78、19.11和43.00 Hz。对应的模态动能分别为1.297×107、2.075×108、1.051×109J,以1阶竖弯作为控制振型,根据Den Hartog方法进行TMD设计,桥梁参数以及TMD设计参数如表1、2所示。 表1 桥梁特性参数 表2 TMD设计参数 图5为TMD安装前后桥梁跨中竖向位移和加速度的变化情况。 (a) 跨中竖向位移时程 由图5可知:考虑车桥耦合后,弹簧质量块过桥时产生了冲击效应,0.3~0.6 s时间内竖向位移出现了较为显著的波动。引入TMD后,跨中位移峰值有所减小,但并不明显。相比之下,TMD使得车桥耦合效应引起的跨中振动速度幅值明显下降,荷载在桥上的最大竖向振动加速度峰值降低约33%。因荷载下桥时所引起的桥梁激振特别明显,所以在0.9 s附近的TMD减振效果更为显著。 图6为TMD安装前后车体振动加速度的变化情况,对于单自由度模型,车桥接触力的变化与加速度趋势一致。由图6可知:安装TMD能够起到降低车体振动加速度和减小车-桥峰值作用力的效果。车体振动峰值加速度最大降幅约为18%,同时,TMD对车体振动的影响并非在车辆上桥瞬间开始,而是随着车辆的前进逐步凸显。 图6 车体加速度时程曲线 考虑到车辆荷载作用下的挠度由静挠度和冲击效应2部分组成,为揭示TMD行程曲线与车-桥耦合动力效应之间的相互关系,定义t时刻TMD质量块的相对运动位移为δTMD(t) δTMD(t)=zb(t)-zm(t) (16) 车-桥动力效应引起的位移为Δzb(t) Δzb(t)=zd(t)-zbs(t) (17) 式中:zb为TMD与桥梁结构连接点在t时刻的动挠度;zd、zbs分别为桥梁计算点t时刻对应的动挠度和静挠度;zm为TMD质量点在t时刻的动位移。 图7为TMD行程曲线δTMD、车-桥系统以及车-桥-TMD系统动力效应引起位移的对比曲线。由图7可知:TMD行程相位与车辆动力效应引起的位移时程相差约1/4个振动周期,TMD的振动相对滞后。对比安装TMD前后的竖向位移峰值可以发现:TMD行程幅值与减振效果呈现明显的正相关特点,即行程幅值越大对车-桥动力效应引起的振动减振效果越好。因此,TMD车致振动的减振效果的关键在于如何在行程限值内提高TMD随动幅值。 图7 TMD行程与动力效应位移时程曲线对比 由于车-桥耦合引起的激振效果受路面粗糙度、车辆荷载和通行速度的影响较大,为此,图8给出了车辆在不同通行速度、质量及路面粗糙度等级情况下的TMD行程计算结果。考虑到TMD行程符合正负交替的振动特点,这里选用特征量的均方根(root mean square,RMS)值和瞬态峰值(maximum transient vibration value,MTVV)作为减振效果评价,计算结果中不考虑车辆下桥瞬间所引起的动力冲击效应。 图8 不同变量的影响分析 由图8可知:随着车速增加以及质量增大,TMD的行程峰值和RMS均相应增加,总体呈现正相关的特点。由于路面粗糙度是通过PSD频谱用随机过程的形式描述,所生成的粗糙度数据具备较强的随机性。因而,路面粗糙度的影响较为不同,在路面粗糙度等级由A下降为B时,TMD行程峰值和RMS值均出现了明显的增加,增幅约2.0倍,而由等级B继续下降时,RMS值的增幅几乎为0,路面等级C时的TMD行程瞬时峰值略低于等级B。 某深水区非通航桥孔采用5×110 m钢箱连续梁,桥面宽33.1 m、高4.5 m,双向六车道高速公路,设计时速100 km/h。由于钢箱梁跨度大,固有振动频率较低,为降低外界激励,尤其是涡振所引发的桥梁振动[19-20]。因此,在相应的跨中设置了TMD减振装置。 桥梁孔跨布置及安装TMD的主梁钢箱标准断面如图9所示。考虑实桥风洞实验的涡振测试结果,将该桥的一阶竖弯作为受控振型,并据此按前述方法进行抗风TMD参数设计。将TMD对称布设在结构第2跨和第4跨,每跨间隔布置4组,其中,单个TMD上限质量取4 500 kg、阻尼比取6%,调频范围为0.72~0.89 Hz,行程限值为±0.3 m[21]。 图9 桥梁断面及孔跨布置 建立5×110 m钢箱连续梁有限元模型,其中,结构纵梁、外伸刚臂和桥墩结构采用空间梁单元模拟,TMD则采用线性弹簧和质量单元模拟,边界条件为墩底固结、墩梁采用耦合方式联结。 采用兰索斯法分析原桥梁结构前三阶竖向振动模态,如图10所示。从振型结构上分析,桥梁结构的前2阶竖弯呈现典型的邻跨反对称特性,说明第2跨和第4跨在车辆荷载激励下容易发生二次激振。 (a) 一阶竖弯0.80 Hz 谐响应分析是验证安装TMD后是否能克服共振、疲劳以及其他受迫振动的有效手段。针对线弹性结构,谐响应分析是以按正弦(简谐)规律变化的载荷作为激励,计算得到出结构稳态受迫振动下对应几种频率的频响曲线,从而方便于直观地预测结构的持续性动力特性。以第3跨跨中为分析对象,图11给出了安装TMD减振系统前后的谐波响应振幅变化规律。由图11可知:TMD的介入显著降低了桥梁结构由1阶竖弯主导的振动幅值,而对高阶竖弯几乎没有影响,由于二阶竖弯对应的跨中峰值较小,所以并未谐波激振中频幅图中显示。 图11 安装TMD前后的频幅曲线 图12为安装TMD减振系统后,TMD与主梁跨中各自的频幅响应曲线。由图12可知:在主梁1阶竖弯频率附近,TMD的响应幅值远大于桥梁跨中区域,而在其他频率范围内,TMD虽然会跟随主梁振动而运动,却振动幅值远小于主梁,难以发挥出减振的效果。另外在同频共振区段,TMD行程幅值达到最大,应当关注是否超过行程限值。 图12 TMD与主梁的频幅变化 为弥补谐响应分析不能考虑激振开始时的瞬态振动的特性,图13为时域内往复激励荷载作用下的桥梁振动和衰减分析结果。由图13可知:在安装TMD后,结构受往复激振后的峰值出现了明显的减小,减振效率约为50%。同时,钢箱自由振动衰减过程时间大幅度较小,等效阻尼比由原来的0.3%提升至3.3%,显著提高了结构的稳定性。 图13 安装TMD前后的时域振动曲线 结合弹簧质量-TMD-桥梁系统振动分析结果,为充分突显车辆对桥的激振作用,以两辆车三轴重车并行作为典型工况,车速80 km/h,车辆信息及布置如图14所示。考虑路面粗糙度级为B,分析安装TMD对车辆通过桥梁振动特性的影响。 图14 双重车激励布置工况 图15为车辆通行过程中TMD的行程曲线。由图15可知:TMD的行程峰值分别在车辆刚抵达第1跨跨中时刻和抵达第3跨跨中时刻,此时的第2跨桥梁结构皆发生了上挠。随着车辆驶入第2跨跨中,TMD振幅开始逐渐减小,减振效果减弱,在车辆驶离跨中到进入第3跨中过程中,TMD的振幅又逐渐增大。这是由于连续梁桥一阶竖弯振型的邻跨反对称性,使得第2跨容易出现反向激振,这也反映出TMD的减振作用的发挥也依赖激励的方向。对大跨桥梁而言,车辆的冲击效应在静位移附近的波动并不显著,所以峰值位移处的减振效果并不理想。 图15 第2跨中TMD行程 图16、17分别为跨中安装TMD前后桥梁跨中竖向位移和跨中竖向振动加速度的动力响应时程变化曲线。由图16可知:相比于静力影响线,考虑路面粗糙度的车-桥耦合振动引起了一定的动力冲击效应,第1跨和第3跨的跨中最大竖向挠度的响应被“放大”。相对而言,桥梁小位移时段和发生上挠位移时段内的车-桥耦合引起的冲击效应更明显。总体来看,安装TMD对位移峰值有减小趋势,但不明显。由图17可知:安装TMD对桥梁加速度的控制效果更为突出,原有竖向振动加速度峰值大幅度降低。 (a) 边跨跨中 (a) 边跨跨中 事实上,由于大跨桥梁低频振动的特性,使得车-桥耦合的冲击效应有一定程度的缓冲和减弱,要准确分析TMD对位移的影响还需分离时程位移中的动力成分进行单独研究。表3从冲击系数的角度出发,对比分析了安装TMD对车-桥冲击效应的影响情况,同时,考虑到加速度正负交替的振动特点,对比了安装TMD前后桥梁竖向振动加速度均方根(RMS)变化情况,其中U1-U3、A1-A3分别为每跨跨中位移和振动加速度。 表3 安装TMD对桥梁结构位移和加速度的影响 由表3可知:考虑车桥耦合的最大冲击系数为8.4%,出现在第3跨的跨中,相对略高于规范给出的5%,安装TMD后,冲击系数降至5.5%,降幅为2.9%,说明安装TMD对车-桥耦合引起的位移中的动力成分有一定的削弱。而由于第1跨和第2跨的车-桥耦合冲击系数本身较小,安装TMD并未产生较大改变。对于因一阶邻跨反对称导致的上挠位移,如果按照冲击系数的概念分析,最大冲击系数仍然出现在第3跨跨中,安装TMD后动力效应降幅为4.3%。相比对位移的影响,安装TMD后桥梁前3跨跨中的加速度RMS值均显著下降,降幅皆在20%左右。 推导了基于动能演化的多自由度结构的TMD控制方法,基于BDANS软件引入Combin14单元建立了车-桥-TMD耦合动力分析系统,分析了经典弹簧质量-简支桥梁模型和5×110 m钢箱连续梁安装抗风型TMD后的车-桥系统振动响应的变化。得到以下结论: (1) 安装TMD对车、桥2个子系统的振动特性均产生一定的影响,使得车-桥耦合效应引起的桥梁振动加速度瞬态极值明显降低,同时,车-桥接触力瞬态峰值也有所下降,车体振动加速度减小。 (2) 稳态受迫振动下,在受控频率附近,TMD的响应幅值远大于桥梁结构,此时更应关注TMD行程限值。瞬态激振下,安装TMD的结构等效阻尼比由原来的0.3%提升至3.3%,结构的稳定性显著提高。 (3) 由于连续钢箱桥梁低频振动的特性,大跨桥梁抗风型TMD对车致振动位移的影响并不明显,但大致服从正相关,即冲击系数越大,减振越明显。相比位移,安装TMD对桥梁振动加速度RMS值抑制更为显著。 (4) 对大跨钢桥而言,车辆荷载的冲击效应并不明显,TMD的作用效果很大程度依赖于是否受到了反向激励,这就使得TMD的减振效果与桥梁结构低阶竖弯模态振型特点相关联,一阶竖弯邻跨反对称的振型更容易激起TMD,使之发挥减振作用。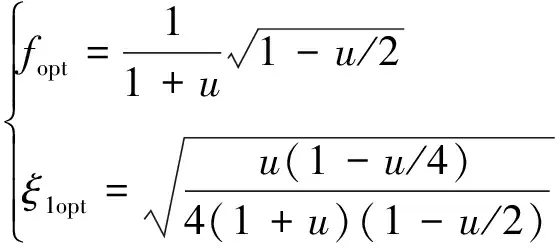
2 车-桥-TMD随机振动耦合分析系统建立
2.1 耦合系统运动方程
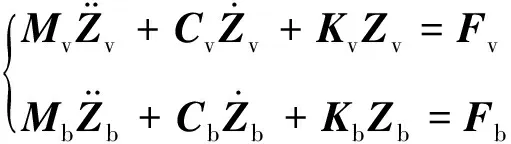
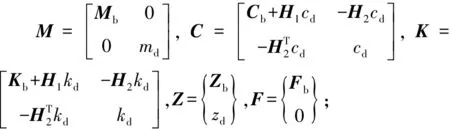
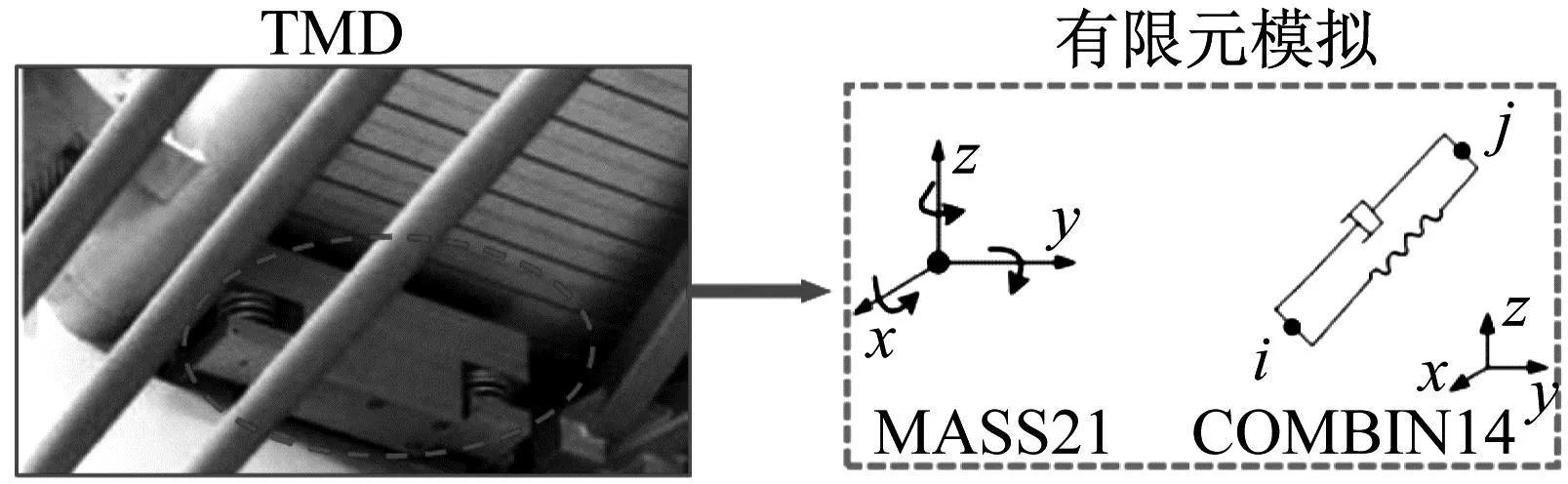
2.2 TMD在有限元中的模拟方法
2.3 车-桥-TMD系统的时域求解
3 算例分析
3.1 模型参数


3.2 计算结果
3.3 参数敏感性分析
4 工程应用
4.1 工程背景
4.2 桥梁动力特性分析

4.3 谐响应分析和动力时程分析
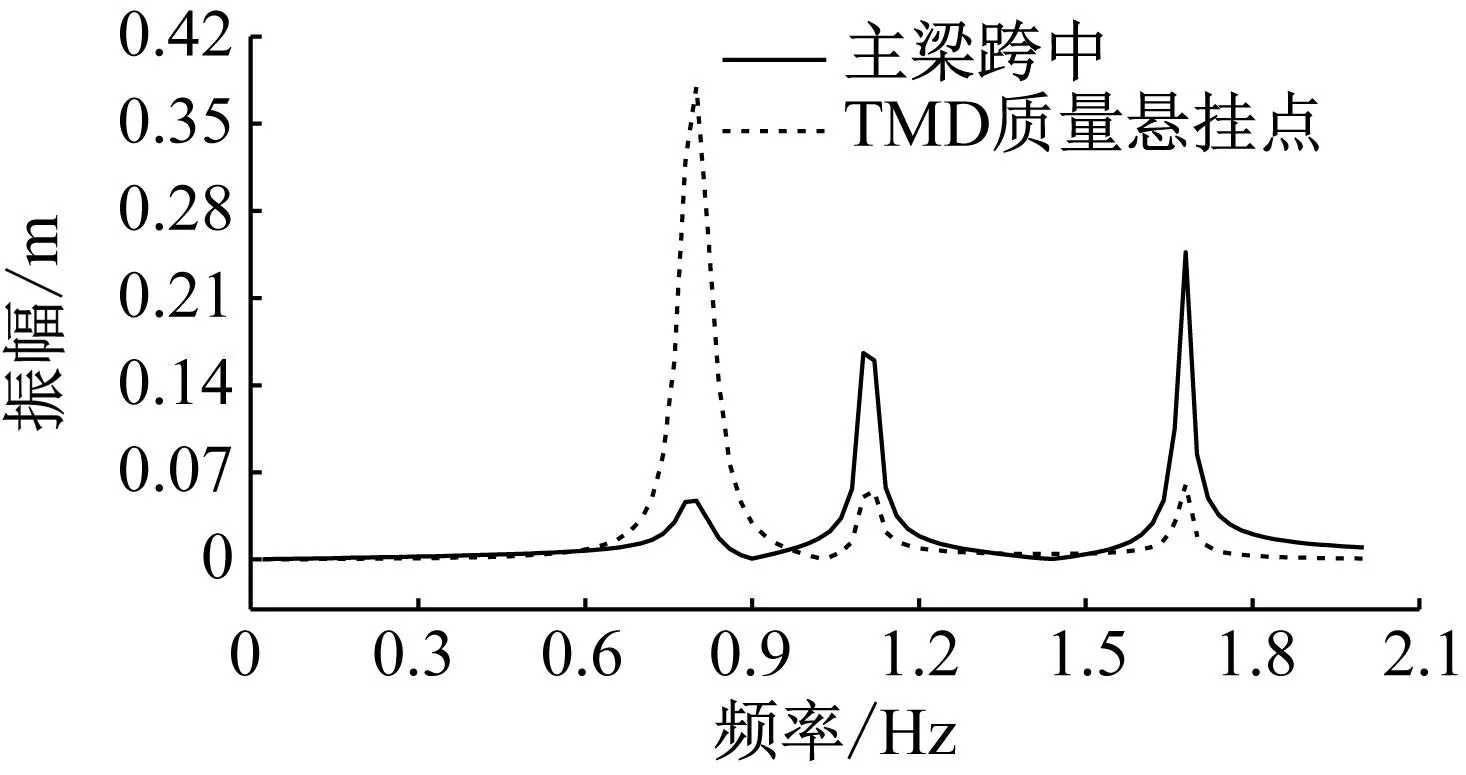
4.4 车辆荷载下的减振效果
5 结 论

