电液3-UPS/S并联稳定平台参数振动特性分析
袁晓明,王维锜,庞浩东,张立杰
(1.燕山大学 河北省重型机械流体动力传输与控制实验室,河北 秦皇岛 066004;2.燕山大学 先进锻压成形技术与科学教育部重点实验室,河北 秦皇岛 066004)
稳定平台通过敏感元件检测设备的位姿变化,利用姿态调整对设备的偏斜进行补偿,隔绝环境的影响以保持设备在惯性空间的相对稳定[1-4]。依据机构类型分类,稳定平台可分为串联稳定平台和并联稳定平台[5-6]。串联稳定平台控制简单、设计成本低,多用于激光定位、卫星通讯、导弹制导、无人侦察机等场合;并联稳定平台具有承载能力强、刚度高、易于实现多轴耦合驱动的特性,在武器发射、海上救援、直升机对接等高精度作业场合有着广泛的应用场景[7-10]。通过采用具有功重比大、响应速度快、累计误差小等优点的电液驱动形式,稳定平台的运动控制精度得到大幅提高[11-12]。但是流体工作介质引入导致的机液耦合现象以及非线性因素使机构的振动特性更为复杂。在实际工况下,驱动液压缸的压力脉动所导致的参数振动不可避免地对稳定平台的姿态补偿与控制精度造成影响,严重制约了稳定平台性能的提升[13-14]。
针对电液驱动的并联机构参数振动的研究,主要有几何方法、数值方法和解析方法三种方法对其进行求解[15-16]。几何方法是在常微分方程理论的基础上,由相轨迹的几何性质进行定性分析的方法。数值法是以非线性微分方程求解为基础理论的分析方法,能够确定在特定参数和初始条件下系统的运动规律,该方法通常用作检验理论结果的一种有效手段。解析法以线性振动理论的精确解为基础,通过近似解析系统的动力学方程,从而分析系统响应规律的方法。近似解析方法种类繁多,例如平均法[17]、摄动法[18-19]等,而多尺度法凭借其对于求解不同问题的高通用性,已在系统模态分析、参数识别、减振避振、故障诊断和状态检测等方面得到广泛应用[20-23]。
但是在研究过程中,对参数振动响应幅值的研究尚未开展。因此,以电液3-UPS/S并联稳定平台作为研究对象,采用多尺度法对机构的参数振动响应理论解析表达式进行求解,在此基础上对参数振动响应特性进行了分析,最后采用数值仿真与模态试验的方法对参数振动模型进行了验证。本项研究可为揭示电液驱动的并联稳定平台的振动机理提供一定的理论基础。
1 电液3-UPS/S平台参数振动建模
由于泵源压力脉动与伺服阀的自激振荡作用,驱动液压缸油腔油液压力不可避免地存在波动,进而造成机构液压刚度的波动。为探究机构在压力波动条件下的振动响应特性,以试验测得的油液压力脉动曲线为基础,构建机构的参数振动方程。
1.1 电液3-UPS/S平台机构
电液3-UPS/S平台结构简图如图1所示。平台由动平台、静平台、三条伸缩支链与一条支撑支链组成。伸缩支链为主动支链,由液压缸进行驱动,液压缸活塞杆由球铰连接至动平台,缸体由万向铰连接至静平台;支撑支链通过球铰连接至动平台,限制了平台的移动自由度,使平台只具有任意方向的转动自由度。
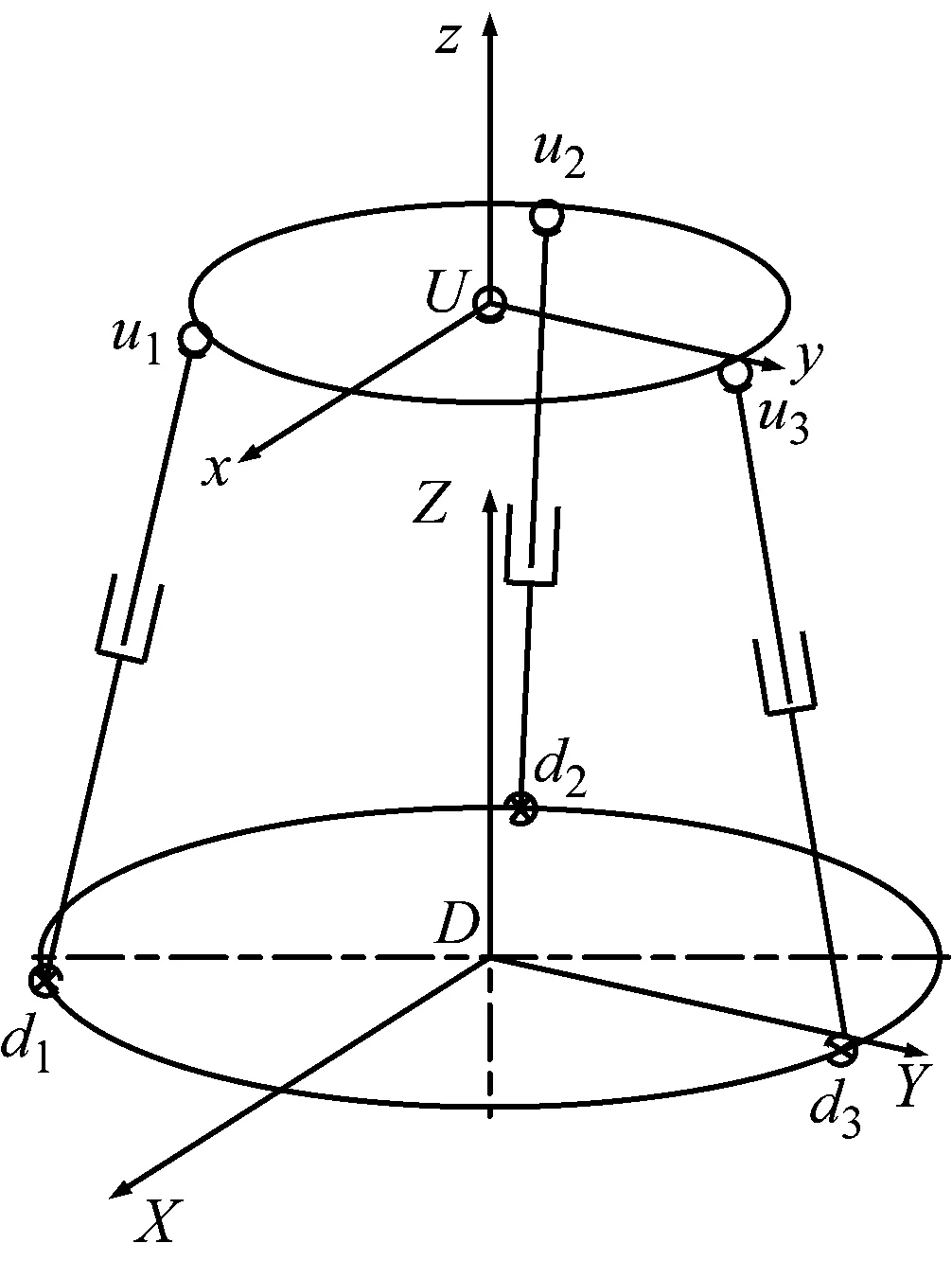
图1 电液3-UPS/S平台简图
1.2 压力波动下油液等效刚度
为求解机构的油液压力波动矩阵,需测量驱动液压缸的油缸压力数据,具体方法如下:
在驱动液压缸的有杆腔与无杆腔处设置测试点并安装压力传感器,通过采集卡将采集到的压力数据输入至计算机以获得系统的压力脉动曲线,最终结果如图2所示。
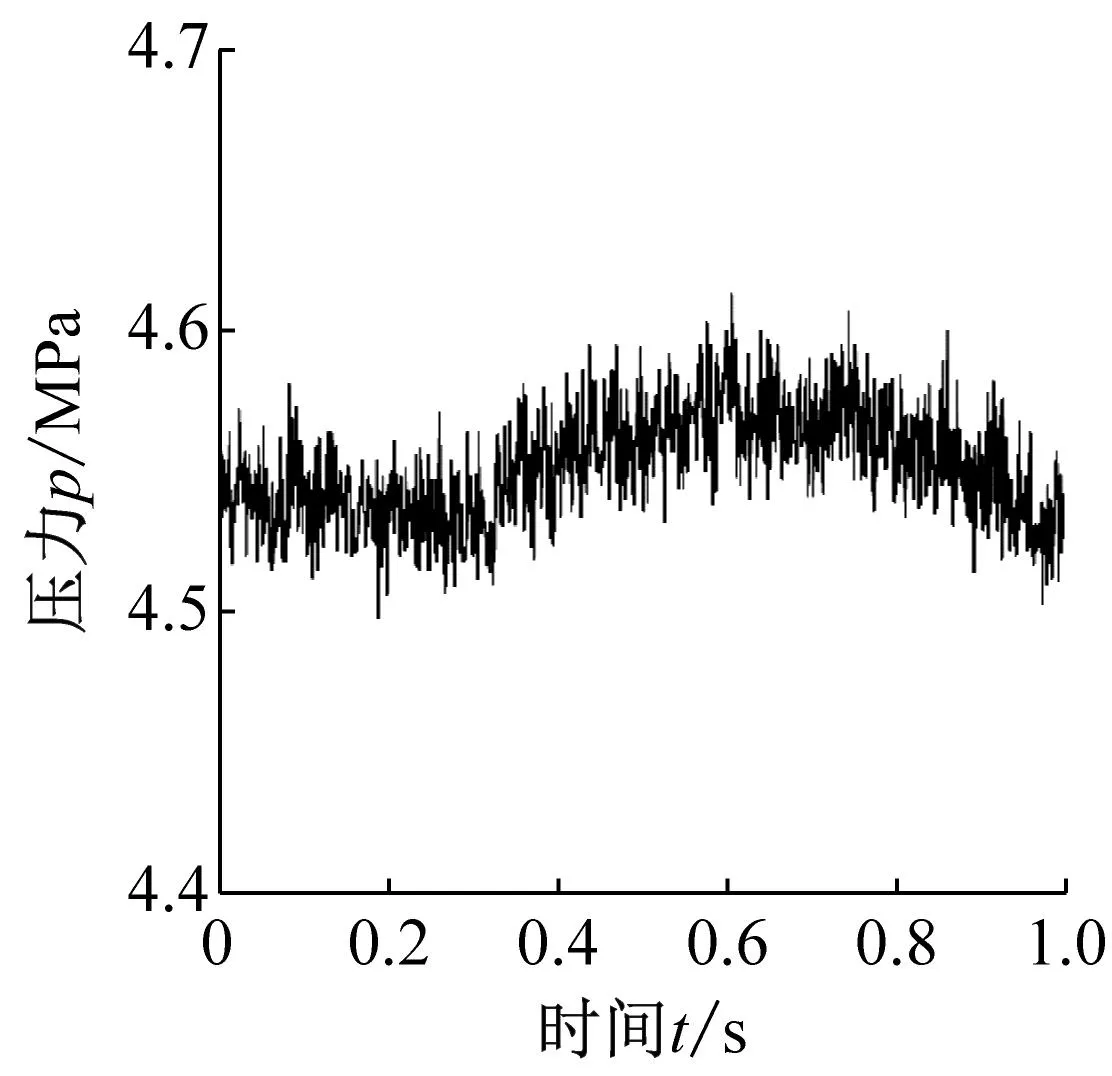
(a) 驱动支链1液压缸有杆腔压力脉动曲线
假设油液压力按照简谐规律变化,则油液压力表示为
(1)
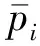
受到支链液压缸油液压力波动的影响,支链中的流体时变等效刚度也会随之发生改变,其表达式为
(2)
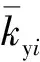
1.3 电液3-UPS/S平台参数振动方程
电液3-UPS/S平台机构在工作过程中,支链液压缸油腔内的油液会被压缩,油液等效刚度可表示为
(3)
式中:kyi为各腔油液等效刚度;ΔFi为各腔油液复位力;ΔLi为各腔油液轴向长度变化,m。
机构运动过程中,液压缸两油腔内的油液在活塞移动过程中轴向位移量相同,可看作弹簧并联的形式,故机构的单支链液压缸度可表示为
kgi=k1i+k2i
(4)
式中:kgi为第i条支链油液等效刚度;k1i为第i条支链液压缸无杆腔油液等效刚度;k2i为第i条支链液压缸有杆腔油液等效刚度,其中i=1,2,3。
设支链液压缸油液压力呈余弦变化规律且分布均匀,则电液3-UPS/S平台机构参数振动动力学方程可表示为
(5)
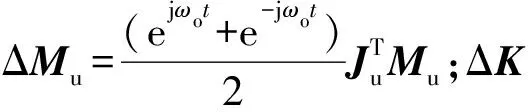
将式(5)正则化即可得到正则坐标下系统的参数振动方程
(6)
式中:CN为正则坐标下阻尼矩阵;Λ为谱矩阵;ΔMN为正则坐标下激振力矩矩阵;ΔKN为正则坐标下流体压力波动矩阵。
2 电液3-UPS/S平台参数振动响应求解
在得到机构参数振动方程的基础上,采用多尺度法对振动响应的解析近似解进行求解,为振动响应仿真奠定理论基础。
2.1 电液3-UPS/S平台主共振响应稳态解析近似解
采用多尺度法求解机构的振动响应解析近似解,设式(5)的二次解析近似解表达式为
ηi=ηi0(T0,T1)+εηi1(T0,T1)+…
(7)
式中,Tn=εnt,ε为小参数量。
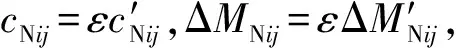
零次幂方程表达式为
(8)
式中,ωni表示第i阶固有频率的稳态值(i=1,2,3)。
一次幂方程表达式为
(9)
式中,MBi为矩阵MB的第i项元素(i=1,2,3)。
当压力波动角频率接近系统的各阶固有频率时,系统将产生主共振,引入协调参量σ,则有:
ω0=ωni+εσ
(10)
求解式(8)、式(9),得到零次解析近似解表达式为
(11)
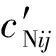
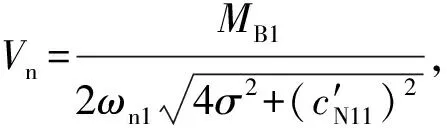
式中:ΔkNij为矩阵ΔkN的第i行第j列元素;MBi为矩阵MB的第i行元素。
则直角坐标系下系统的主共振响应理论解析近似解为
x=ψT(η0+εη1)
(15)
同理,可对压力脉动角频率接近其余各级固有频率时,机构的主共振响应稳态解析近似解进行求解。
2.2 电液3-UPS/S平台组合共振响应稳态解析近似解
与主共振响应分析类似,采用多尺度法对系统组合共振响应进行求解,设方程的解如式(16)所示
(16)
将式(16)代入式(5),根据小参数量同次幂相等的条件,可得到组合共振响应的零次幂方程和一次幂方程如下
零次幂方程:
(17)
一次幂方程:
(18)
以激励频率接近一阶固有频率与压力脉动角频率之和为例,引入谐调参数σ
ω0=ωn1+ωe+εσ
(19)
求解可得组合共振响应零次解析近似解表达式为
(20)
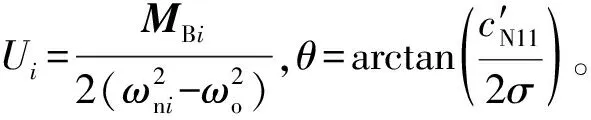
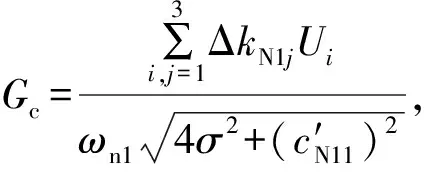
(21)
(25)
(28)
(29)
(30)
(31)
(32)
则直角坐标下系统的组合共振响应为
x=ψT(η0+εη1)
(33)
3 电液3-UPS/S平台参数振动特性分析
电液3-UPS/S平台机构结构参数如表1所示。

表1 电液3-UPS/S平台结构参数
将表1相关结构参数代入式(5)求解机构在随机位姿α=10°,β=10°,γ=28°的固有频率稳态值,结果如表2所示。

表2 电液3-UPS/S平台固有频率稳态值
3.1 电液3-UPS/S平台主共振响应分析
电液3-UPS/S平台压力脉动频率ωe为6.28 rad/s,若机构在随机位姿α=10°,β=10°,γ=28°下所受力矩矩阵表达式为
(34)
则可计算激励频率接近各阶固有频率时机构主共振响应曲线如图3所示。
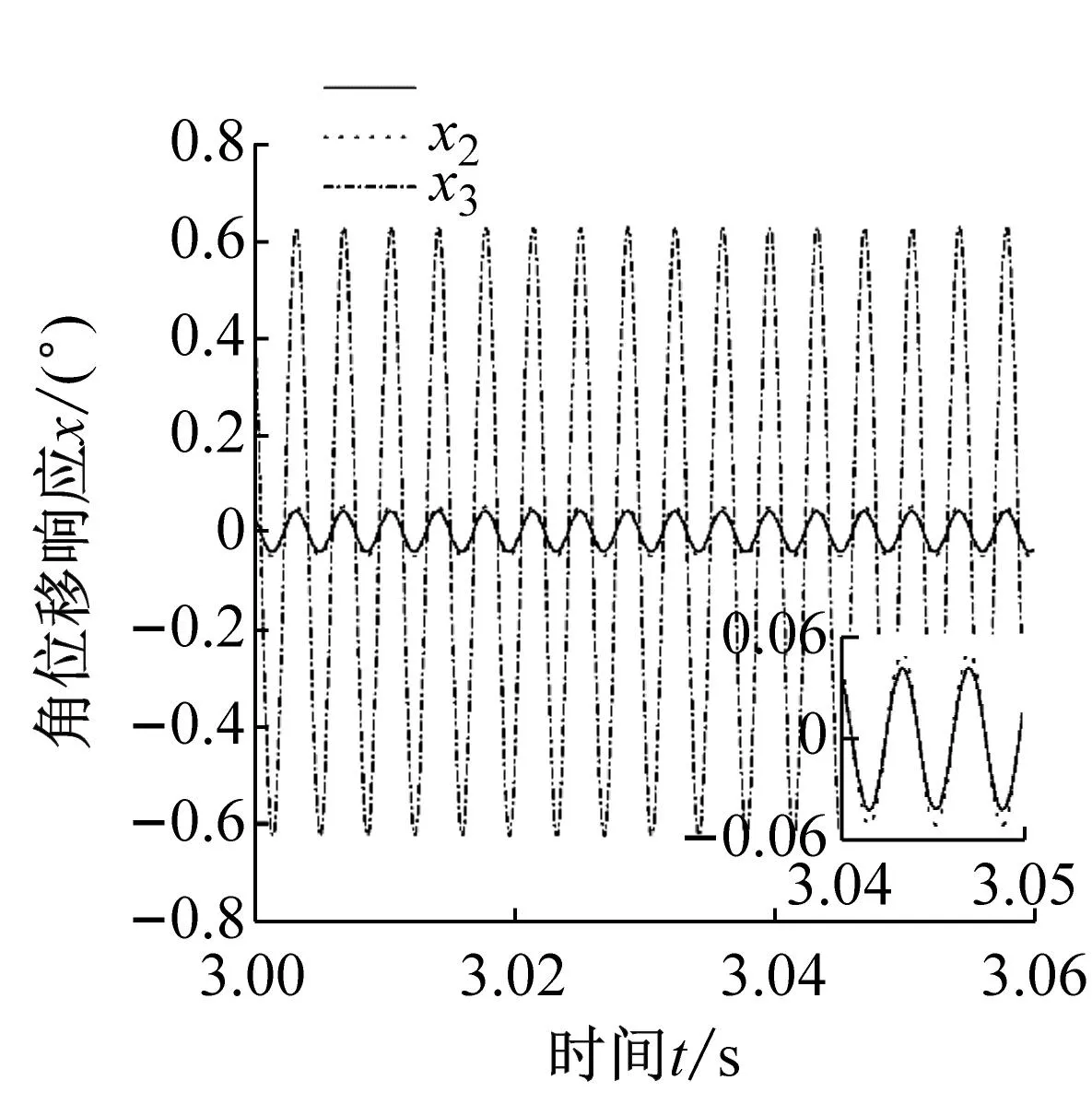
(a) ω0≈ωw1稳态响应时域曲线
由图3(a)和3(b)可以看出,当激励频率接近一阶固有频率时,机构在偏转方向上振动响应幅值最大,最大振动响应幅值为0.623°,机构在俯仰和回转方向上的振动响应幅值近似相等。由图3(c)~3(f)可知,当激励频率接近机构的二阶、三阶固有频率稳态值时,机构依次在俯仰、回转方向上振动响应幅值达到最大,俯仰方向最大振动响应幅值为0.029 1°,回转方向最大振动响应幅值为0.016 2°,此时其余方向的振动响应幅值较小,与主振型一致。
3.2 电液3-UPS/S平台组合共振响应分析
保持机构各参数不变,计算机构的组合共振响应曲线如图4所示。
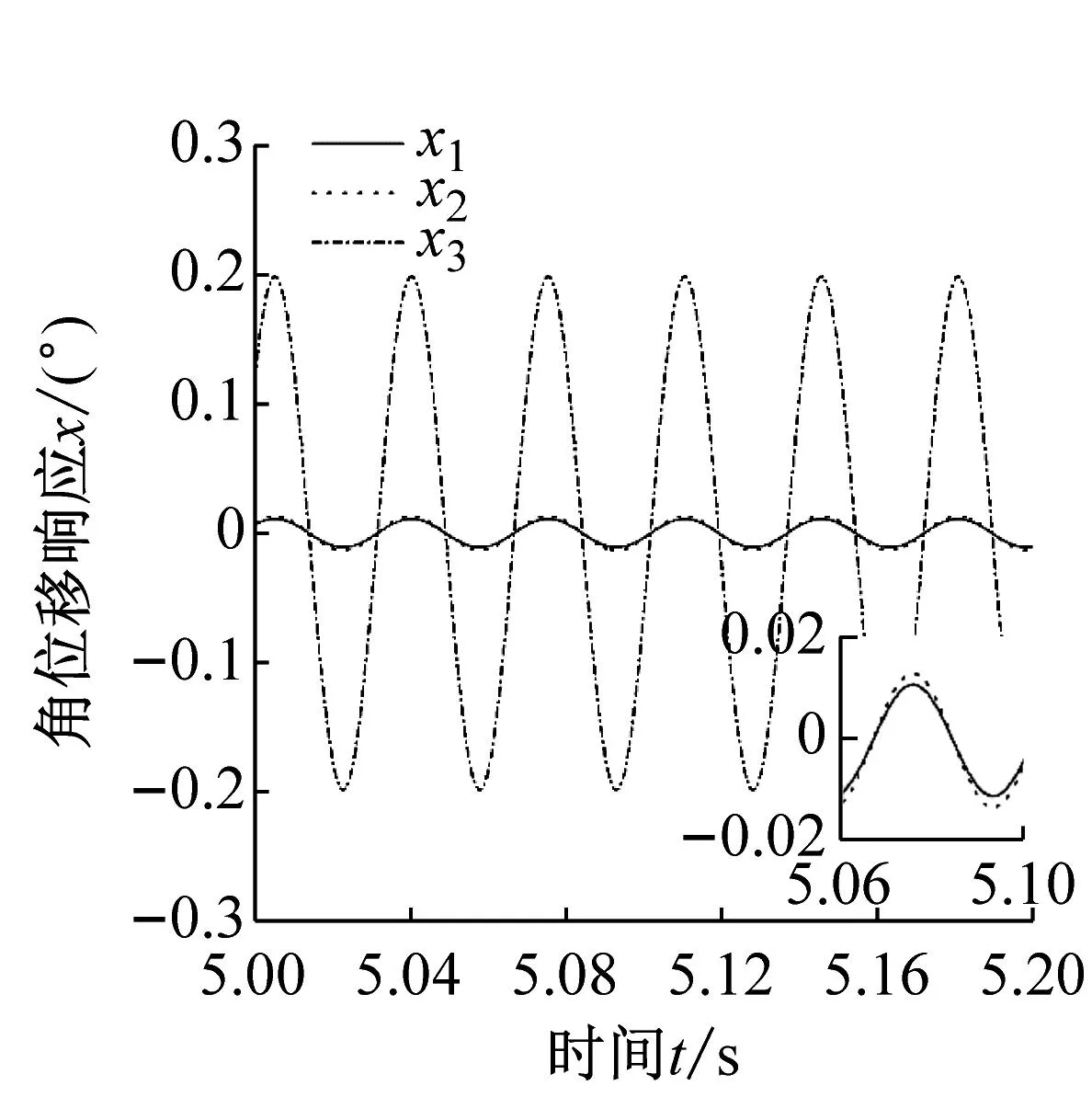
(a) ω0≈ωw1+ωk稳态响应时域曲线
由图4(a)可知,当激励频率接近机构的一阶固有频率稳态值与压力脉动频率稳态值的组合频率时,机构偏转方向的振动响应最大,远大于回转、俯仰方向的振动响应。由图4(b)可知,在ωw1+ωk处,各方向上的振动响应幅值达到最大,且回转和俯仰方向上的振动响应近似相等。由图4(c)~4(f)可知,同主共振响应类似,当外部激励频率分别接近二阶、三阶固有频率稳态值与压力脉动稳态值的组合频率时,机构俯仰、回转方向上的振动响应幅值达到最大。对比图3和4可以看出,机构主共振的主导频率为机构各阶固有频率的稳态值,组合共振的主导频率为各阶固有频率稳态值与压力脉动频率稳态值的组合频率。
3.3 电液3-UPS/S平台工作空间振动响应幅值分析
机构参数振动的响应幅值是机构姿态的函数。通过时域与频域分析可知,当激励频率接近分别接近一阶固有频率稳态值、一阶固有频率稳态值与压力脉动频率稳态值的组合频率时,机构的振动响应幅值远大于接近其他固有频率的情况。当平台用于维持设备水平方向稳定时,偏转方向上姿态补偿角度变化范围较小,主要通过回转、俯仰方向上的运动进行角度补偿。根据工作空间搜索理论,当偏转姿态角度γ=28°时,回转、俯仰姿态角度连续变化范围最大,因此以该位姿作为初始工作空间,激励频率分别接近一阶固有频率稳态值、一阶固有频率稳态值与压力脉动频率稳态值的组合频率为例,计算机构的主共振与组合共振振动响应幅值,最终结果如图5所示。
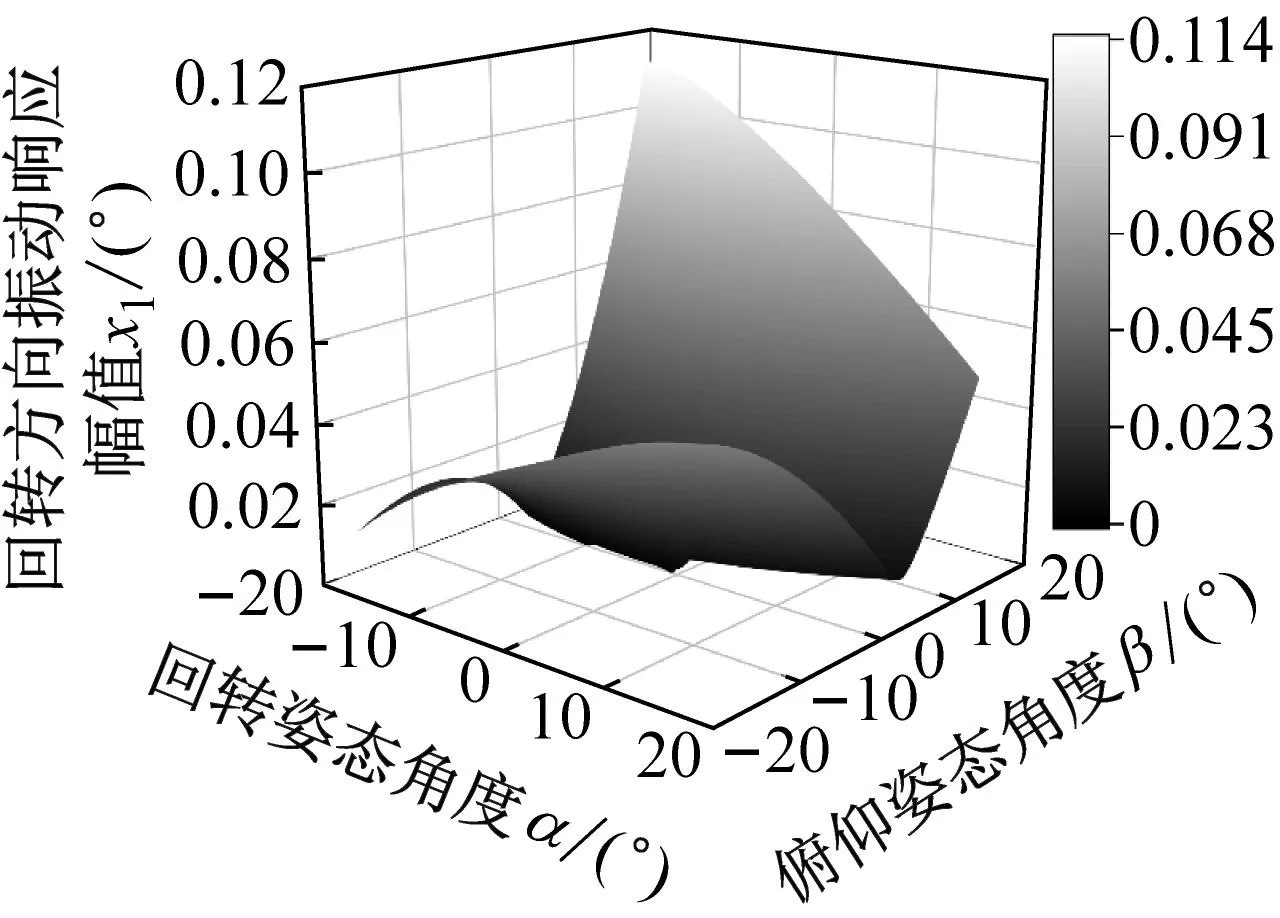
(a) 回转方向主共振响应幅值
由图5(a)、5(d)可以看出,机构在回转上的主共振与组合共振响应幅值在俯仰姿态处于初始位姿时数值较小,对回转方向的姿态变化不敏感,初始工作空间内,机构主共振响应幅值最大值大于组合共振响应幅值最大值。由图5(b)、5(e)可以看出,机构在俯仰方向上的主共振与组合共振响应幅值在回转姿态处于初始位姿时数值较小,对俯仰姿态角度的变化不敏感。由图5(c)、5(f)可知,机构偏转方向上的主共振与组合共振响应幅值大于机构在回转、俯仰方向上的响应幅值,且变化呈现一定的对称性,初始工作空间内,机构主共振响应幅值最大值小于组合共振响应幅值最大值。对应主振型分析结果,在激励频率分别接近机构一阶固有频率稳态值、一阶固有频率稳态值与压力脉动频率稳态值的组合频率的条件下,机构的主共振与组合共振响应幅值均大于其他方向上的振动响应幅值。
4 电液3-UPS/S平台参数振动模型验证
为验证机构参数振动模型的正确性,采用数值仿真方法计算振动响应与模态试验测量机构固有频率相结合的方法对机构的模型进行验证。
4.1 基于数值法的参数振动模型验证
以机构处于随机位姿α=10°,β=10°,γ=28°,激励频率分别接近机构一阶固有频率、一阶固有频率与压力脉动频率的组合频率为例,利用四阶龙格库塔法对机构稳态响应进行求解,得到机构的时域响应曲线如图6所示。
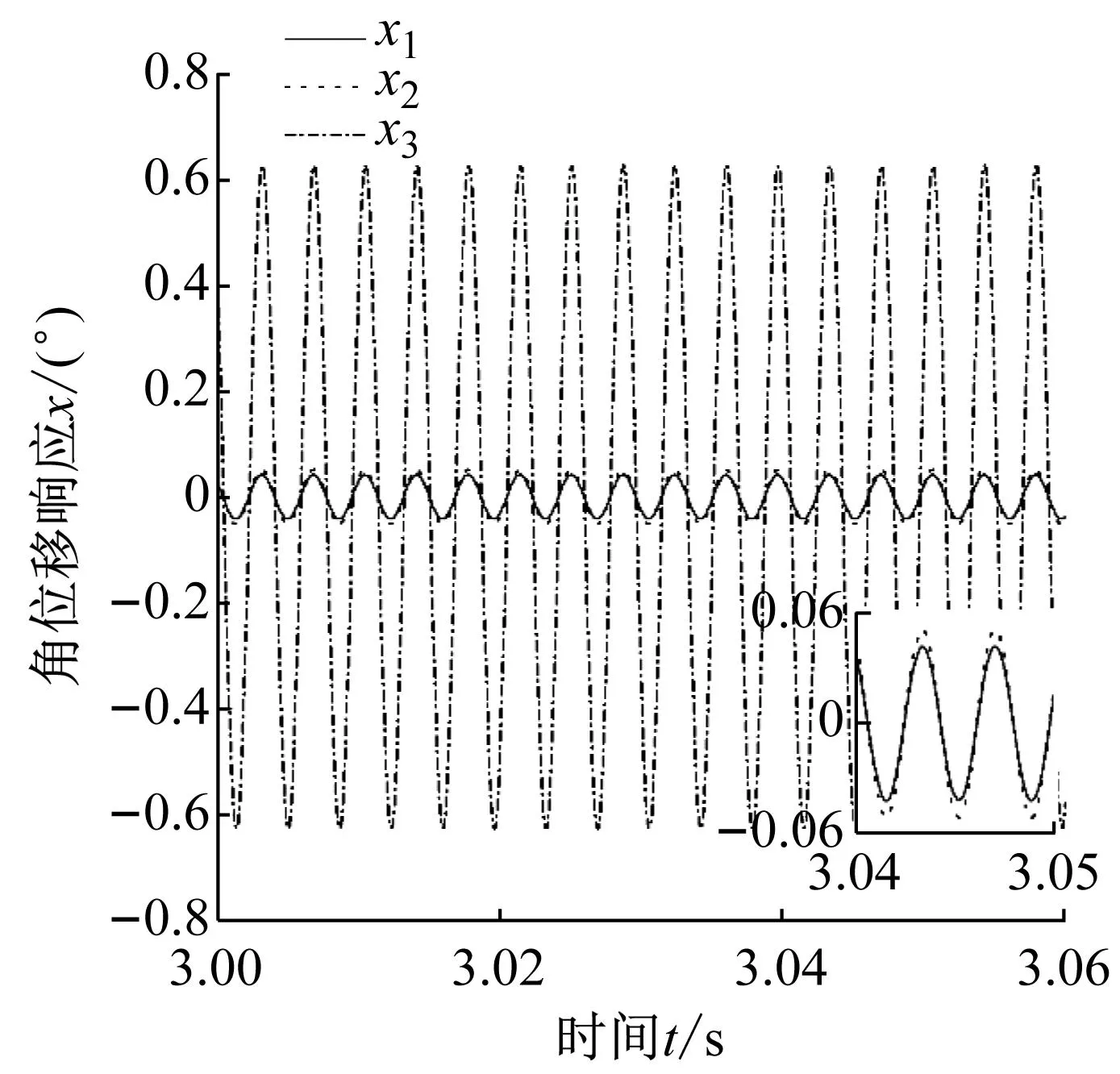
(a) 主共振稳态响应数值解时域曲线
由图6(a)可知,数值解法所求得的机构主共振稳态响应呈现简谐波动,回转、俯仰、偏转方向上的角位移响应最大值分别为0.041 7°,0.050 9°,0.624 7°,数值解与理论解的最大误差为0.47%;由图6(b)可知,机构发生组合共振时,回转、俯仰、偏转方向上的角位移响应最大值分别为0.011 0°,0.012 7°,0.189 9°,数值解与理论解的最大误差为4.2%,由此可以验证机构参数振动理论模型的正确性。
4.2 电液3-UPS/S平台样机模态试验
采用脉冲激振法对电液3-UPS/S平台样机进行模态试验。样机如图7所示。平台振动响应数值解结果如表3所示。
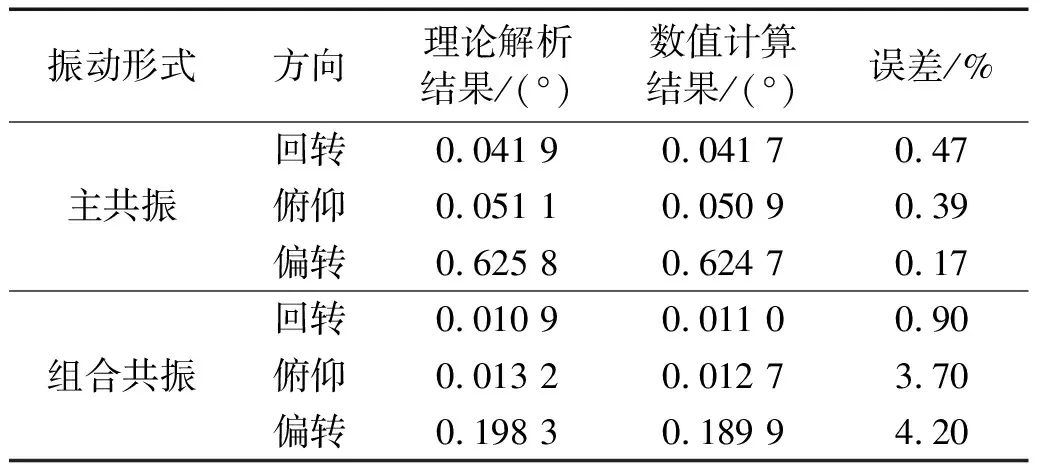
表3 电液3-UPS/S平台振动响应数值解结果

图7 电液3-UPS/S平台样机
为验证自由振动理论模型的正确性,采用脉冲激振法测量3-UPS/S平台样机在随机位姿α=10°,β=10°,γ=28°下的固有频率,试验原理图如图8所示。力锤敲击样机动平台给予脉冲激励,样机的加速度变化通过加速度传感器收集并传递至下位机,由此产生的力信号经由力锤自带的传感器传递至下位机,最终下位机将收集到信号传输至电脑进行储存。模态试验系统图如图9所示。试验结果如表4所示。
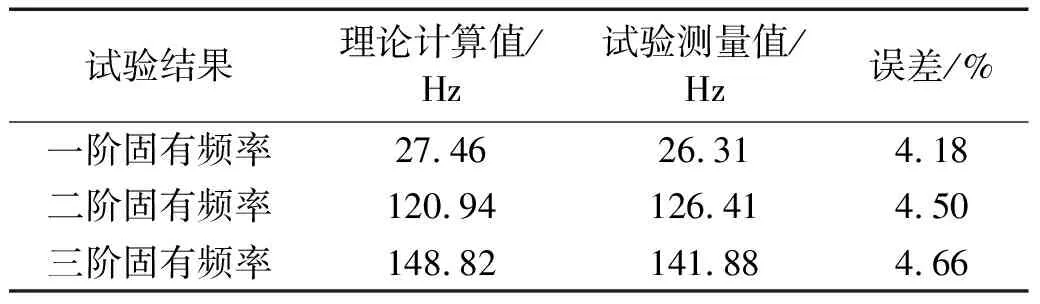
表4 模态试验结果
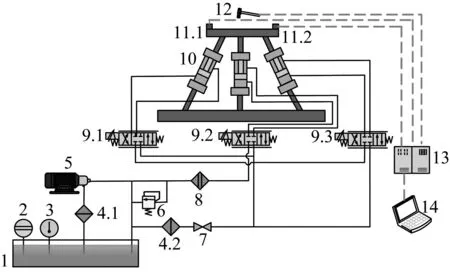
1.油箱;2.液位计;3.液温计;4.过滤器;5.电机、液压泵;6.溢流阀;7.截止阀;8.精过滤器;9.伺服阀;10.平台样机;11.加速度传感器;12.力锤;13.下位机;14.计算机。

(a) 模态试验平台
试验中所用采样频率为640 Hz,因此满足采样定理要求,采集信号具有可信度,试验所采集的激励信号与振动信号的时域曲线如图10所示。
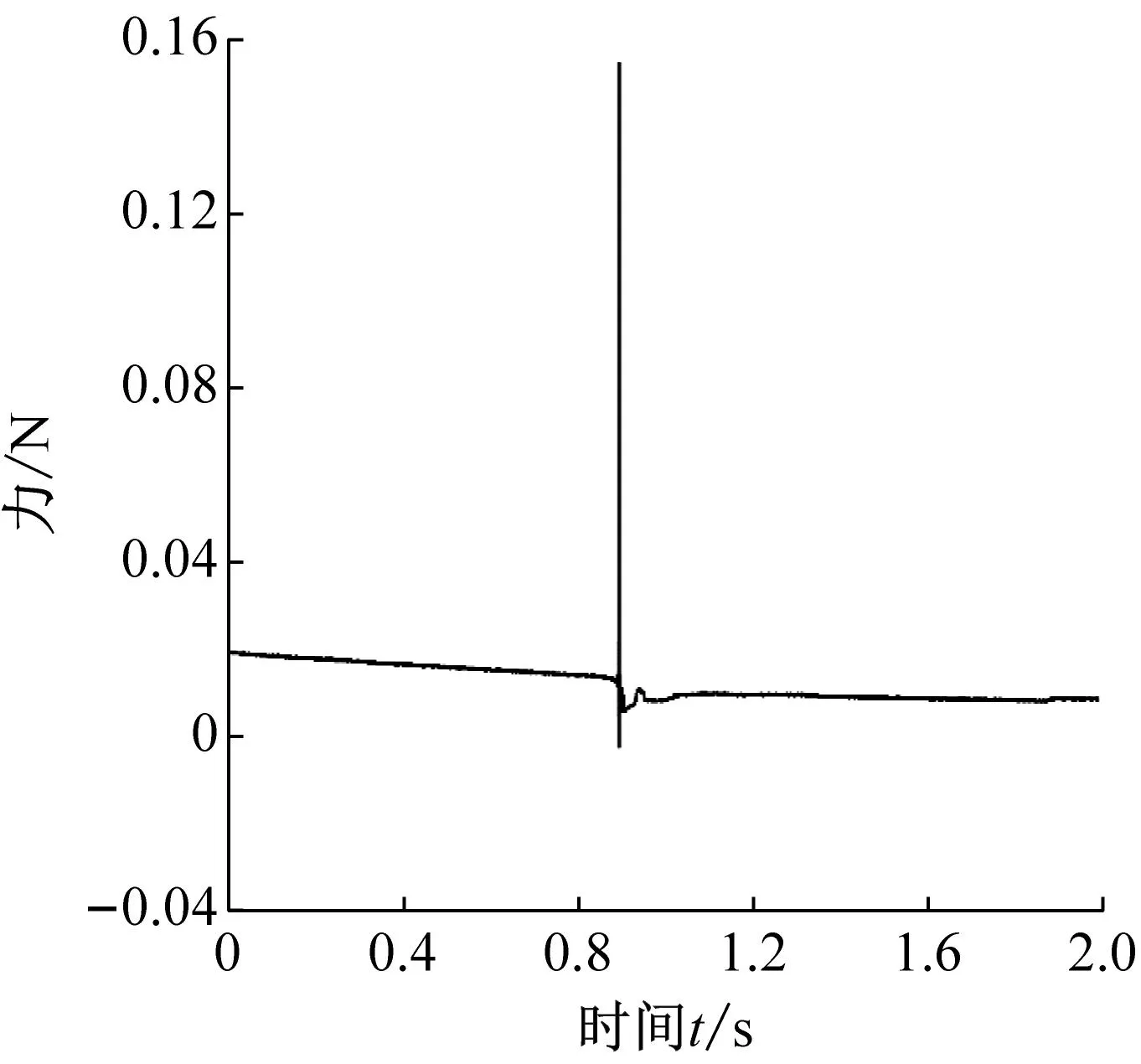
(a) 力信号曲线
对图10所得数据进行数据处理,可得到样机响应信号的功率谱密度曲线如图11所示。观察图11可以看出,曲线在26.31 Hz,126.41 Hz和141.88 Hz处具有明显峰值,通过与机构固有频率理论值对比,理论值与试验值的最大误差为4.66%,因此可验证理论模型的正确性。
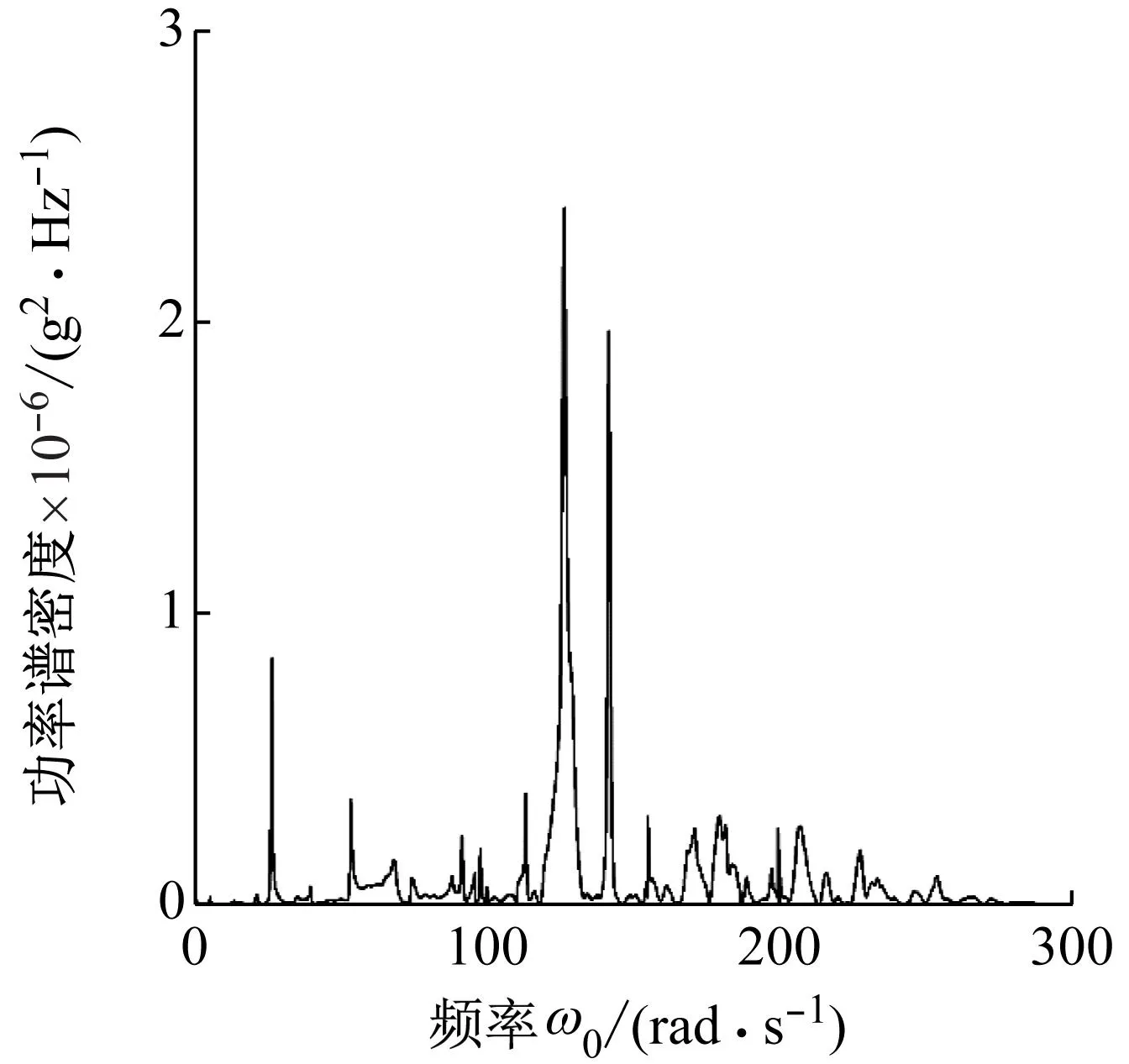
图11 功率谱密度曲线
5 结 论
(1) 机构的主共振主导频率为机构的各阶固有频率;组合共振主导频率为机构的各阶固有频率与压力脉动频率的组合频率,此时机构的各阶固有频率起调节作用;
(2) 初始工作空间内,机构在回转、俯仰方向上的主共振与组合共振响应幅值对同方向的姿态变化不敏感,且当激励频率分别接近机构一阶固有频率、一阶固有频率与压力脉动组合频率时,机构在偏转方向的振动响应幅值远大于其余两个方向上的振动响应幅值;
(3) 采用四阶龙格库塔数值仿真方法与模态试验对参数振动模型进行验证,结果表明:数值解与理论解之间的最大误差为4.20%,固有频率理论值与试验值之间的最大误差为4.66%,可验证参数振动模型的正确性。

