借助公式合理应用,回归函数本质创新——2023年全国数学新高考Ⅱ卷第8题

⦿ 江苏省宜兴市第二高级中学 杨文英

数列是《普通高中教科书·数学》选择性必修课程中函数主线的重要内容之一,也是历年高考数学试卷中的主干知识之一.在每年高考中,数列都是一个重要命题点,也是高考命题中考查“四基”,以及考查创新意识与创新应用的一个重要的风向标,备受各方关注.

1 真题呈现

高考真题(2023年高考数学新高考Ⅱ卷·8)记Sn为等比数列{an}的前n项和,若S4=-5,S6=21S2,则S8=( ).

A.120 B.85 C.-85 D.-120

本题目简单明了,解题的思路可以从等比数列的公式与性质应用两个视角切入,利用相应的公式加以合理变形与转化,或利用对应的性质加以构建与应用,都可以有效化归与转化,实现问题的解决.

2 真题破解

2.1 等比数列的公式应用

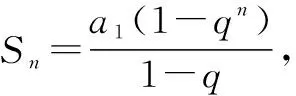
方法1：利用等比数列求和公式.

方法2：方程求解法.

解析：依题知,等比数列的公比q≠1.由S4=-5,S6=21S2,联立方程可得

解后反思：根据等比数列的通项公式、求和公式等来处理与解决问题,是解决等比数列中最基本的一种解题方法,通过公式的展开,结合不同问题场景加以灵活化简、巧妙运算等.在实际解题时,要注意数列中的通项公式、求和公式等的灵活应用,以及公式中的整体思维、函数与方程思想等的应用.

2.2 等比数列的性质应用

等比数列的性质应用的前提就是初步掌握一些与等比数列的通项、求和等相关的基本性质,利用对应性质合理构建相应的关系式,为问题的进一步求解提供条件,是解决问题的“巧技妙法”.

方法3：利用等比数列求和公式的变形.

解析：依题意可知,有Sm+n=Sn+qnSm,结合S6=21S2,可得S6=S3×2=(1+q2+q4)S2=21S2,可得q4+q2-20=0,解得q2=4.所以S8=S2×4=(1+q4)S4=(1+42)×(-5)=-85.故选:C.

解后反思：等比数列求和公式的变形形式Sn+m=Sn+qnSm,以特殊形式,并结合等比数列的求和性质应用来转化与解决问题.利用相关等比数列的变形公式法处理问题时,其关键在于充分挖掘各Sn中的下标的倍数关系或和差关系,结合变形公式的熟练掌握来分析与应用.

方法4：利用等比数列的性质.

解析：在等比数列{an}中,Sn,S2n-Sn,S3n-S2n也成等比数列的性质,可知S2,S4-S2,S6-S4,S8-S6也成等比数列.

当S2=-1时,结合(S6-S4)2=(S4-S2)(S8-S6),可得S8=-85.

综上分析,可得S8=-85.故选:C.

解后反思：根据等比数列求和公式的性质,即Sn,S2n-Sn,S3n-S2n也成等比数列,合理构建一个新有关等比数列求和的线性关系式的等比数列,并利用等比数列的性质进一步解题.该等比数列的性质应用也离不开各Sn中的下标的倍数关系,这与等比数列的变形公式法有异曲同工之妙.

方法5：等比数列的函数性质法.

解析：在等比数列{an}中,令Sn=A(1-qn),A≠0,由S6=21S2,可得1-q6=21(1-q2),解得q2=4(q2=-5<0,舍去).

解后反思：根据等比数列求和公式的函数性质Sn=A(1-qn),A≠0,借助待定系数法,通过等比数列的求和性质应用来分析与解决问题.回归数列的函数本质,借助等差数列或等比数列的通项公式、求和公式所对应的函数性质,合理构建对应的含参关系式,具有普通性,解题更加灵活巧妙.

方法6：构造法.

解析：构造数列{bn},其中bn=a2n-1+a2n,结合等比数列的性质可知,数列{bn}是等比数列.

设等比数列{bn}的公比为p(这里p=q2>0,q为等比数列{an}的公比),可得1+p+p2=21,解得p=4(或p=-5<0,舍去),结合b1+b2=b1+b1p=-5,解得b1=-1,所以S8=S4(1+p2)=-5×(1+42)=-85.故选:C.

解后反思：根据条件合理构造新数列——从首项起,连续两项之和为新数列的一个项,利用等比数列的性质知其也是等比数列,进而构建相应的关系式加以分析与求解.借助构造思维,引入新数列,使得问题的破解更加直接,更有针对性,解决起来也方便快捷.构造法是创新思维与创新应用的一个重要表现.

3 变式拓展

该等比数列是确定的,因而也可进一步确定其通项公式与前n项和公式的表达式.

变式1记Sn为等比数列{an}的前n项和,若S4=-5,S6=21S2,则an=______.

变式2记Sn为等比数列{an}的前n项和,若S4=-5,S6=21S2,则Sn=______.

以上变式问题,由于等比数列的首项与公比的差异,因而都有两个答案,不能遗漏,否则容易导致错误.

4 教学启示

4.1 抓住数列本质,回归函数应用

数列作为离散函数的典型代表之一,是函数主线的一个重要分支.因此,在实际解决数列问题时,往往要回归数列的函数本质,抓住数列的函数属性,挖掘出相关数列(等差数列与等比数列)的概念、通项公式、求和公式等,以及这些基础知识与函数之间的内在联系,借助函数的观点来合理揭开数列神秘的“面纱”,有效构建联系,进而利用函数的性质与方法来解决数列问题,从而使得数学知识更加系统化,培养学生数学的整体意识,以及用联系发展的眼光学习数学、应用数学等.

4.2 倡导“一题多解”,实现“一题多得”

借助一些典型例题,特别是高考真题的“一题多解”,在进一步巩固与提升基础知识的基础上,拓宽解题思路、技巧方法等,从而开阔学生思路、发散学生思维,加深对问题的“通性通法”的认识与掌握.通过解决问题的“巧技妙法”的应用,进而挖掘相关问题的本质与内涵,提升各方面的能力.

在此基础上,利用问题的“一题多解”,不断研究探索,回归问题本源,深入进行“一题多变”,巧妙实现问题的“一题多得”,聚合数学思维的基础上又加以开拓,特别是在变式中寻找通法,在探究中升华能力,研究之路定会越铺越远.这样可以很好全面提升数学基础知识、思想、方法、技巧等,是综合应用能力、创新应用能力等方面提升的一大表现.