反套路 重计算 孕思想——2023年全国甲卷数学理科试题评析与反思

⦿ 四川省温江中学 王奋际 张 君 杨永清

2023年高考早已落下帷幕,笔者作为一线数学教师,结合自己和部分同行做全国甲卷理科数学试题的感受,以及笔者的学生在考场上和考后的感受,对2023年全国甲卷数学理科试题进行评析与反思.笔者所在学校的学生大致处于中等及中等偏上的水平,对试卷整体的感受有一定的代表性.

1 全面考查而重点突出

2023年高考全国甲卷数学理科试题较2022年甲卷数学理科试题,难度有所增加,但总体保持平稳.试卷没有偏题、怪题,注意控制文字数量和阅读理解难度,与2022年甲卷(约1 600字)相比,2023年甲卷约1 300字,减少约19%.但题目简洁不等于试题简单,表面看平平无奇,内里却蕴含深刻思想.

1.1 知识考查有重点

统观全卷,全面考查高中数学知识,分布合理,兼顾基础性、综合性和创新性.某些板块与其他板块联系广泛,比如三角函数板块,第7,10,11,12,13,16,21等近三分之一的题目都不同程度对其进行了考查.

1.2 素养考查有侧重

喻平教授指出:“逻辑推理、直观想象是基础,数学运算是媒介,数学建模和数据分析是应用,其本质是数学抽象.”可见,六大核心素养联系紧密,亦有侧重.

令人印象最深刻的有两点:一是直观想象素养的考查,以第11,18题为代表的立体几何题目,让学生暴露出不少问题,学生不甚适应,考后普遍感觉难算、难想;二是数学运算素养的考查贯穿全卷,学生普遍反映选填题运算较花时间,个别学生甚至因为选填题用时过多,导致解答题时间不足.

1.3 难度设置反套路

全卷送分题不多,都需要一定的运算与思维,但难度特别大的题目没有.单独看选择题第12题、填空题第16题等传统意义上的压轴题,难度并不大;第1题开始就体现了一定的抽象性,第10,11题难度适中,基本与第12题持平;学生原本认为应该容易“过关”的第18题难度陡升,对学生心理素质和临场决策能力是一个巨大的考验.

1.4 情感态度价值观

情境创设方面,全卷坚持立德树人,紧跟时代大潮.第6题以滑雪为背景,呼应2022年北京冬奥会后的冰雪经济;第9题以志愿者公益活动为背景,引导服务社会的意识;第19题以研究臭氧效应的科学实验为背景,引导环境保护的意识.

全卷服务于优秀创新人才的选拔.第10,11,21题都有一定的创新性,思维难度大,运算量也大,要求学生兼具创新品质与坚强意志.

反思与启示1:注重知识跨板块、跨学科的迁移应用.如,三角函数、平面向量等.事实上,人教A版高中数学(2019年)新教材不仅增加了很多实际应用例子,还专门设置了数学探究栏目,比如在数学必修第二册中就有“用向量法研究三角形的性质”探究栏目.

反思与启示2:对学生临场决策能力的训练很重要,如改变解答题出现顺序、不同难度题目出现顺序、难题对应知识板块等,让学生对高考试卷的变化有心理准备.

反思与启示3:在平时教学中注重结合正能量、社会热点情境,关注教材中有现实背景的例题教学.如,一般科学实验的方法、个人所得税纳税方式等.

2 立体几何中的反套路

本套试卷的立体几何题成为学生答题过程中的拦路虎.普遍反映选择题中第11题比第12题更难,解答题中第18题让很多学生不知该用哪种方法,决策困难,影响全卷答题.

第18题:如图1,在三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=90°,AA1=2,A1到平面BCC1B1的距离为1.

图1

(1)证明:A1C=AC;

(2)已知AA1与BB1的距离为2,求AB1与平面BCC1B1所成角的正弦值.

此题第(1)问的难点在于条件“A1到平面BCC1B1的距离为1”,同时一条棱长未知.对于线面距离的处理,切入点较多,但每个切入点又都有其难度,学生在选择方法时容易陷入困难.

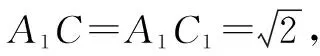
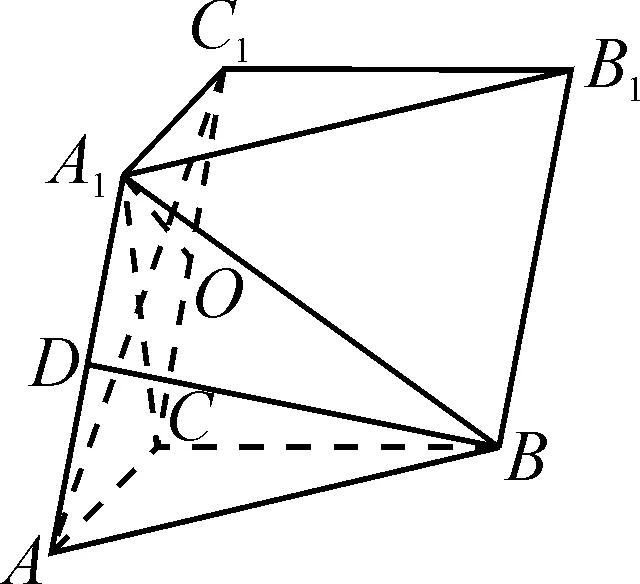
图2

代数角度:以C为原点,CA,CB,CA1分别为x,y,z轴建立空间直角坐标系,但CA,CB的长度未直接给出,需要先设未知数,通过列方程组解得,部分考生在考场上难以准确算出答案.

此题第(2)问也可以从两个角度分别思考.

本题的解答,综合运用几何和代数两种方法,可使解题过程得到最大的简化,充分体现立体几何的考查要有几何味,不能一味靠建立坐标系来解答.

反思与启示4:在教学中,采用单元整体教学,帮助学生建立知识的整体架构并体会研究问题的一般观念,正如章建跃博士谈到的“研究对象在变,研究套路不变,思想方法不变”,让学生掌握并熟练应用这些“不变”的思想方法.学生不能因为学习了空间直角坐标系,就忽略研究几何问题的一般方法.

3 处处可见的数学运算

数学运算素养是六大核心素养的媒介,本套试卷重点进行了考查,计算量较以往增加了不少,特别是选填题部分,给考生的时间分配提出了挑战.

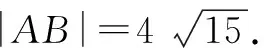
(1)求p;

此题第(2)问条件简洁,图形简单,比较容易入手选择面较广,可以设直线MN的方程,也可以设点M,N的坐标,转化为不等式求最值问题,还可以考虑用抛物线焦半径公式或极坐标解题,转化为三角函数求最值问题,但具体操作时又会遇到不同的情况.

图3

反思与启示5:新课程标准指出,数学运算素养包括理解运算对象、探究运算思路、选择运算方法、设计运算程序、求得运算结果等.因此,教学中除了训练数学运算的速度、熟练度外,还要培养合理选择运算方法和程序的能力.比如,从几何、代数、数形结合等不同角度思考问题;利用函数、向量、不等式、三角函数等不同的数学工具完成计算.

4 关注数据分析的过程

本套试卷对概率统计的考查,给出了列联表的生成过程,统计味十足.

如,第19题,难度不大,展现了一个简单的科学实验过程,如何将连续数据(体重增加量)转化为二元分类数据(是否小于中位数),再利用卡方检验回答“小白鼠在高浓度臭氧环境中与正常环境中体重的增加量是否有差异”的问题.“小白鼠在高浓度臭氧环境中与正常环境中体重的增加量是否有差异”是没有固定答案的,如果改变数据分类标准,如用下四分位数、上四分位数等代替中位数,可能得到不同的结果.

无独有偶,2023年新高考Ⅱ卷19题也是关于标准的选定,题目告诉考生:没有一个临界值能够做到不误诊、不漏诊,只能尽量满足少误诊、少漏诊.

反思与启示6:统计学的学科逻辑与其他高中数学内容不一样,推理方法上属于不完全归纳,统计推断有可能犯错,结论具有不确定性,统计对结论的判断标准有好与坏之分,而非对与错.教学中让学生准确理解统计思想,有助于考场上迅速理解题意.

5 抓基础促进综合能力

全卷落实“四翼”考查要求.以综合性的考查为例,第10题则综合了三角函数图象与直线方程,第21题则综合了导数、不等式和三角函数.但笔者认为,基础性、综合性、创新性与应用性的考查并不独立.

(1)当a=8时,讨论f(x)的单调性;

(2)若f(x)

此题第(2)问是典型的恒成立求参数范围问题,学生从高一学习函数内容开始,就知道此类问题可以含参讨论或分离参数,学习导数后还可以灵活选择切线等更多方法,这些都是高中数学解题的“童子功”,体现了基础性.同时,三角函数最具特点的性质有周期性、有界性等,抓住特点解题就不难,这是需要学生建立的基本观念.

反思与启示7:本题的解答,切入点是高中数学同类问题的基本方法,利用三角函数的核心性质,解题时可以用到换元、数形结合、研究特殊点、放缩、洛必达法则等常用技巧.教学中,综合性难题的突破应该是建立在基础知识、基本技能之上的.这也是新课程提出的,让学生明确研究一个对象的基本套路,在一般观念下研究数学对象.

综上所述,2023年全国甲卷数学理科试题体现了新课程理念,为一线教师指明了教学方向,是一套精彩的好试卷.