新高考,新动向:评近几年高考试题

⦿ 苏州市吴江区苏州湾外国语学校 陈亚娟

近几年高考数学试题的设计遵循《普通高中数学课程标准(2017年版)》的基本要求,充分落实“立德树人”的根本任务,坚持在稳定中求创新,贯彻并渗透高中生在德智体美劳等方面全面发展的教育方针,同时借助高考试题合理回归数学教材,引导平时教学与学习过程中注重对数学基础知识、基本技能的理解与掌握,重视数学本质,注重应用意识、核心素养和学习潜能,突出对数学思想、方法和各种能力的考查,本文中以往年的几道高考题为例展开说明.

1 渗透德育,弘扬文化

例1日晷是把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,若点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( ).

A.20° B.40° C.50° D.90°

分析：理解题目条件,把空间几何问题平面化处理,利用过球心的大圆,把对应的点、线放在平面几何中加以分析与处理.

解析：过球心O、点A以及晷针的轴截面如图1所示,其中CD为晷面,GF为晷针所在直线,EF为点A处的水平面,GF⊥CD,CD∥OB,∠AOB=40°,∠OAE=∠OAF=90°,所以∠GFA=∠CAO=∠AOB=40°.

图1

故选:B.

点评：以数学文化巧妙设置问题,破解的关键是借助平面几何图形中的角度求解立体几何问题,巧妙把数学文化与平面几何加以融合,考查数学建模、直观想象、逻辑推理等核心素养.

2 适度创新,考查潜能

试题设计在继承并保持以往高考中常规题型的同时,进一步发扬并创新,别具匠心地设计了创新新颖的开放性试题.同时设计了数学内涵丰富、设问角度新颖、解答灵活的创新题.这些试题需要较强的审题能力,可以全面考查考生的综合素养.

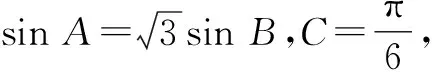
若以上问题中的三角形存在,求c的值;若问题中的三角形不存在,说明理由.

分析：对应问题中,给出两角的关系式以及第三角的值,利用正弦定理构建两边之间的比例关系,借助余弦定理加以综合应用,合理构建三角形三边之间的密切关系,结合不同条件的选择,进一步加以分析,正确判断,合理求解.

点评：新高考中引入的数学开放创新题,难度一般比较适中,考查主干知识,通过条件或结论的合理开放来创设情境与设置问题.具体破解时,可以结合不同选择项的有效选择,从不同角度来分析与处理,充分体现知识的选择性、思维的广阔性以及应用的综合性等,为进一步提升考生的探究意识、创新意识以及应用意识等提供理论指导与方向,培养创新精神.

3 层次分明,多题把关

高考试卷都是按照一定的梯度加以合理呈现,深度上“由浅入深”,难度上“由易到难”,梯度上“阶梯递进”,角度上“拾阶而上”,充分考虑考生的思维习惯与能力差异,进行多角度、多层次的设置,同时加以巧妙分步设问,有效分散难点,合理区分,多题把关.

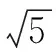
分析：根据空间几何体的基本条件与直观想象,数形结合,通过合理构建空间几何中对应几何元素之间的位置与数量关系,结合降维思维,从三维空间转化为二维空间,将立体几何化归为平面几何,结合圆的弧长以及相应的圆心角大小来求解交线长问题.

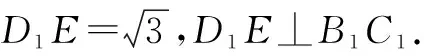
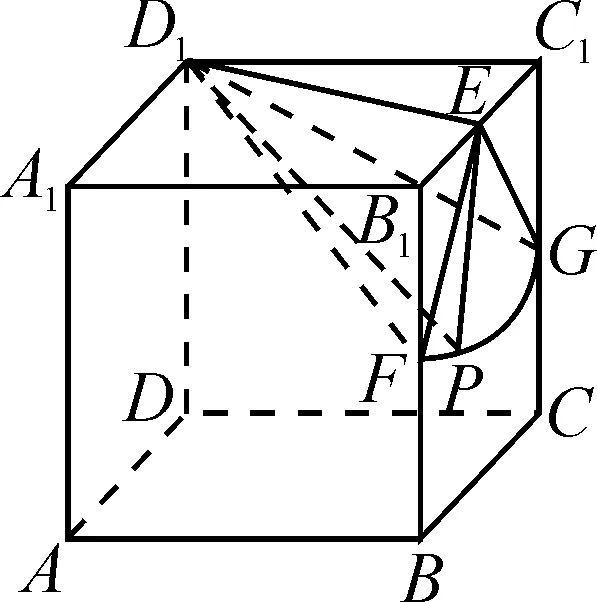
图2

由直四棱柱的定义可知,BB1⊥平面A1B1C1D1,于是可得BB1⊥D1E.又BB1∩B1C1=B1,所以D1E⊥侧面BCC1B1.

点评：此题结合具体空间几何体,巧妙将空间问题与几何问题加以联系,串联起空间问题与平面问题.解答此类问题的关键是把空间问题转化为平面问题,化“动”为“静”,直观想象.立体几何分析法具有较好的直观想象与逻辑推理核心素养,也是利用几何法处理此类问题的主要依据.

4 突出难点,常考常新

近年高考数学试卷充分体现了选拔性,突出对高中数学重点知识与重点内容的考查,特别是主干知识(三角函数与解三角形、数列、立体几何、圆锥曲线以及函数与导数等)的考查,同时关注数学思想方法、数学能力、数学应用等方面的融合与应用.特别是多选题以离散型随机变量的分布列作为最后一题,填空题以立体几何作为最后一题.

A.若n=1,则H(X)=0

B.若n=2,则函数H(X)随着p1的增大而增大

D.若n=2m,随机变量Y所有可能的取值为1,2,……,m,且P(Y=j)=pj+p2m+1-j(j=1,2,……,m),则H(X)≤H(Y)

分析：根据题目条件中新定义的创新公式,结合选项中的不同参数值以及对应的结论,借助创新公式以及随机变量的概率、均值等相关知识,综合函数、不等式等的基本性质来分析与处理,从而巧妙判断.

解析：选项A,若n=1,则p1=1,log21=0,所以H(X)=-p1log2p1=-log21=0,故选择A正确.

故选:AC.

点评：借助新定义所对应的创新公式来创设情境,巧妙设置创新应用问题,以多选题的形式来综合应用,合理进行信息迁移,融合众多的数学知识与应用来巧妙构建数学模型,综合考查数学基础知识、数学思想方法和数学能力等,是创新定义、创新应用、创新题型等多层面“创新”的综合体.

总之,近几年的新高考数学试题进一步完善并推进新课程改革,强调回归数学教材,回归数学本源,回归数学课堂,重视数学概念,重视数学思想方法,也借助高考试题加以合理引导与指引,从而真正实现高中数学教学与数学应用的回归,逐步培养并强化学生的数学核心素养.

2023年命题比赛获奖论文之五：