单元教学设计与核心素养培养——以“平面向量”单元教学为例

⦿ 江苏省宿迁中学 倪文林

1 问题提出

在《普通高中数学课程标准(2017年版)》中,对应“课程基本理念”部分第一次创新性地提出“数学学科核心素养”这一重要理念.对于数学学科核心素养的培养与养成,一直渗透于数学教学与学习过程中,成为数学活动中的一种常态.

数学学科核心素养的培养与养成,对于教学与学习有一定的指导与目标意识,那么在高中数学教学单元中如何加以实施,能够更加有效培养并提升数学核心素养,促进学生的全方位发展呢?本文中以“平面向量”单元教学为例,结合实例就数学学科核心素养的培养加以阐述,以期抛砖引玉.

2 问题解决

2.1 从数学问题中结合抽象加以数学运算

借助平面向量的概念与公式等相关知识,合理构建对应的关系式等,通过数学变形与转化,合理利用数学运算来转化与应用.

例1〔福建省泉州市2023届高中毕业班质量监测(三)数学试卷(2023年3月)·8〕已知平面向量a,b,c满足|a|=1,b·c=0,a·b=1,a·c=-1,则|b+c|的最小值为( ).

解析：在平面直角坐标系xOy中,设向量a=(1,0),b=(x1,y1),c=(x2,y2),如图1所示.

图1

因为a·b=1,a·c=-1,b·c=0,所以x1=1,x2=-1,x1x2+y1y2=0,则y1y2=1.

所以|b+c|的最小值为2.

故选择:C.

点评：本题根据平面向量“数”的结构属性,通过平面直角坐标系的构建加以数学运算,合理引入平面向量的坐标,利用题设条件确定对应坐标的关系,利用基本不等式的放缩、三角函数的应用等来确定向量和的模的最值.

2.2 从逻辑推理中归纳总结加以直观想象

借助平面向量的相关数据信息,特别是向量的位置关系(平行或垂直等),结合题设条件通过合理的逻辑推理,构建与之对应的平面几何图形加以直观想象,从而利用图形直观分析解决平面向量问题.

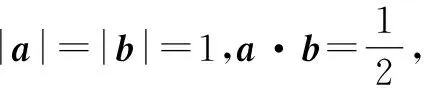
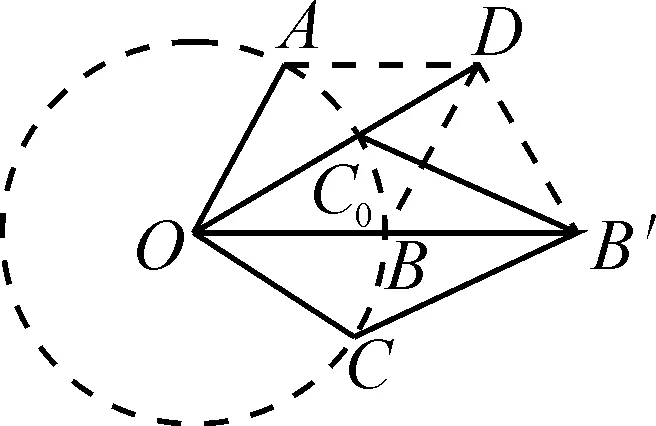
图2

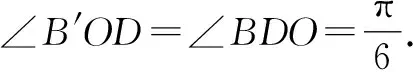
故选择:B.

点评：本题合理通过平面向量“形”的结构特征,借助向量投影的定义加以直观形象处理是解决平面向量数量积的最值中比较特殊的一种技巧方法.这里借助局部与整体的平面向量的投影思维来处理,思维视角不同,解题思维一致,殊途同归.局部视角需要必要的变形与转化,整体视角的要求使得图形更加复杂,各有利弊.

2.3 从数学思维中合理应用加以逻辑推理

类似于特殊值思维等,都是平面向量及其应用中最为常用的一些基本技巧方法.特别对于一些小题(选择题或填空题),抓住问题的本质,通过合理巧妙的逻辑推理,对于解决平面向量及其相关的应用问题有很好的效益.

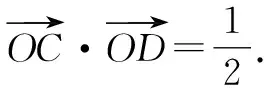
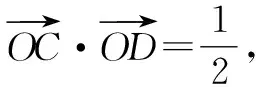
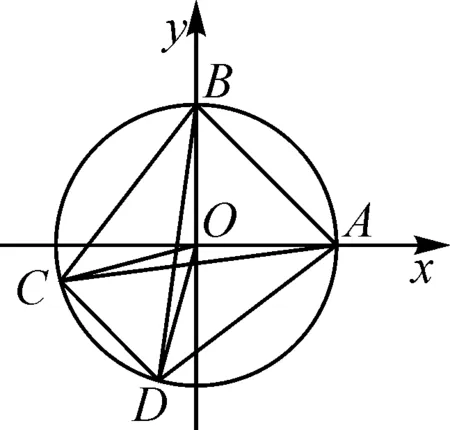
图3

故选择:A.

点评：抓住平面向量“形”的结构特征,从“形”的思维视角切入,结合“形”的位置关系等合理分析与处理.特别是涉及“形”中的对称性、特殊思维等的应用,可以巧妙逻辑推理与数学运算.

2.4 从问题本质中合理转化加以数学建模

从题目条件的本质入手,结合平面向量的概念、运算、性质等加以巧妙转化与化归处理,合理构建数学模型,进而借助熟悉的数学模型来分析与解决相应的平面向量问题.

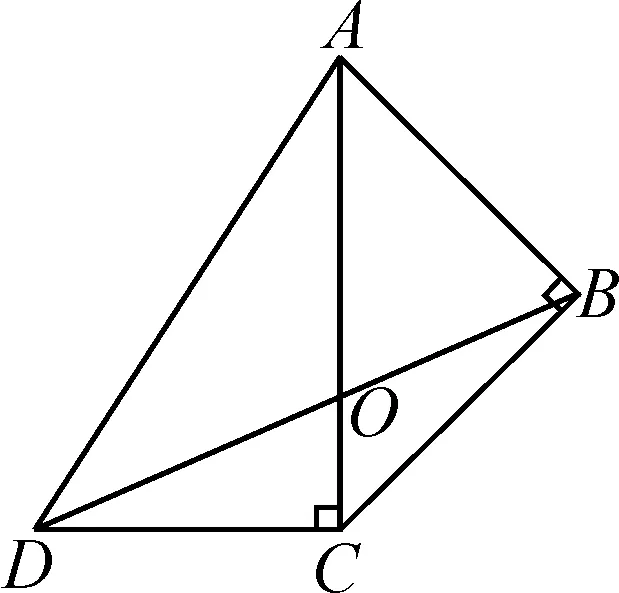
图4

解析：在△BCD中,由BC=CD=1,∠DCB=90°+45°=135°,可得∠BDC=22.5°.

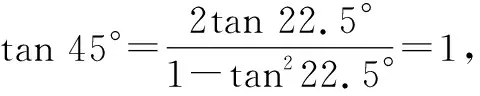
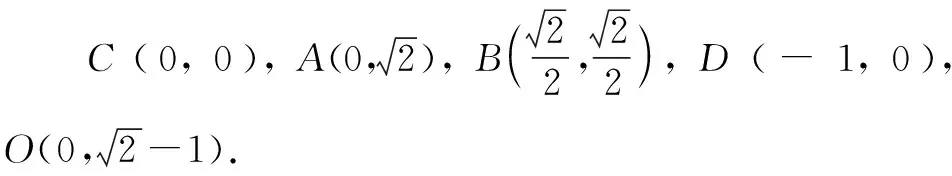
图5

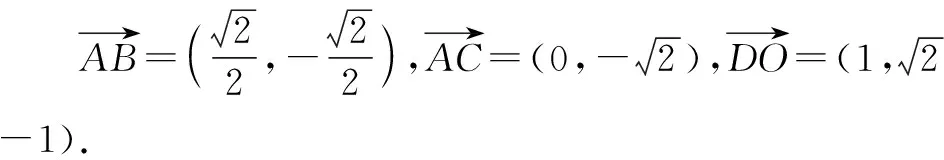
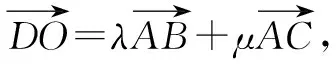
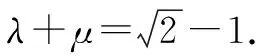
故选择:A.

点评：求解平面向量的线性关系中的系数问题,合理构建数学模型是解题的关键.这里通过抓住平面向量“数”与“形”的双重性质,可以从“数”的视角,也可以从“形”的视角来处理.“数”与“形”的融合与拓展,为平面向量问题的分析与求解提供了基本的思维方式.

3 感悟反思

相应的数学核心素养的培养与养成,对于具体的知识模块来说仁者见仁,智者见智.在实际教学与学习过程中,要充分扎根于课堂,借助平面向量这一模块知识,从本质上加以合理挖掘与拓展,就数学核心知识、数学核心素养等方面,巧妙应用,有效实施.

特别在单元教学过程中,教师要根据平面向量模块知识的本质与特点,从“数”与“形”两个本质属性入手,在课堂教学与学习中加以渗透,提升学生数学能力与数学核心素养.