三维球床几何稀疏条数长特征线加速方法

郭 建,郭 炯,李 富,*,严 睿,邹 杨

(1.中国科学院 上海应用物理研究所,上海 201800;2.清华大学 核能与新能源技术研究院先进核能技术协同创新中心 先进反应堆工程与安全教育部重点实验室,北京 100084)

特征线法是实现球床高温气冷堆复杂几何全堆芯中子输运最有前景的方法[1]。在数学上,特征线法是一种广泛应用的偏微分方程解析解法,20世纪70年代,Askew[2]将偏微分方程特征线法和中子输运方程的离散纵标法、碰撞概率法结合起来,发展出了求解中子输运方程的特征线法。中子输运特征线法在求解区域按照离散纵标法产生的角度方向稠密布置大量的特征线,角通量在特征线上逐段解析求解,并通过积分得到网格标通量。中子输运方程的求解在特征线上完成,因而特征线法对求解区域几何和材料分布没有任何要求,非常适合于具有随机分布燃料球的高温气冷堆中子输运求解。

迭代次数多和计算速度慢是限制特征线法应用的主要因素。因此,特征线法通常作为组件计算中的二维输运计算方法或者全堆芯计算2-D/1-D方法[3]的径向二维输运计算方法。WIMS[4]、CASMO[5]和HELIOS[6]等组件计算软件均采用特征线法作为非均匀几何中子输运计算方法。为了解决特征线法计算速度慢的问题,CASMO、OpenMOC[7]和DeCART[8]等程序采用粗网有限差分(CMFD)方法降低迭代次数,可实现具有宏观方形规则区域的加速,显著减少了计算时间。基于2-D/1-D方法的MPACT[9]和NECP-X[10]等程序除了采用CMFD方法进行数值加速外,还实现了在集群计算机上的大规模并行,能够在分钟量级给出单个算例的结果。

为了突破数值加速方法中宏观规则几何的局限,Yamamoto[11]提出了广义粗网再平衡(GCMR)方法,从理论上指出GCMR方法可应用于非规则几何的粗网格,然而没有给出具体可行的方法。柴晓明等[12]提出了广义粗网有限差分(GCMFD)方法并引入了用于计算非规则几何耦合系数的宽度因子,但宽度因子无法从理论上直接给出而只能在迭代过程中逐渐逼近,此外,非规则几何区域网格边界面积和体积通常只能近似计算,这都减弱了GCMFD方法的加速效果。Smith[13]提出了长特征线加速方法(macro-track transport acceleration method),不需要计算网格界面的中子流,具有和特征线法同样的几何处理能力,可真正实现任意几何特征线法加速。

本文在长特征线加速方法中引入稀疏条数长特征线方法,可在不降低加速方程精度的前提下极大地缩短计算时间,解决三维几何加速方法计算量大的问题。

1 传统长特征线加速方法

长特征线加速方法将连续几个线段合并为一个长特征线段,如图1所示,实线段表示长特征线。根据特征线法中的角通量,见式(1),可以得到长特征线上的源,见式(2):

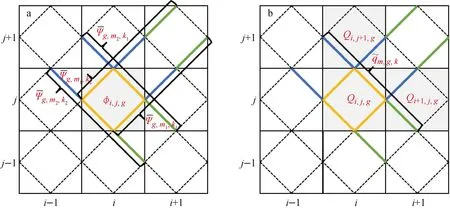
a——网格标通量计算方法示意图;b——长特征线源计算方法示意图图1 长特征线加速方法网格标通量和长特征线源计算方法Fig.1 Calculation method of grid scalar flux and macro-track source for macro-track transport acceleration method

Ψi,g,m,k(s0,out)=Ψi,g,m,k(s0,in)e-τi,g,m,k+

(1)

Ψip,g,m,k(sp,in)

(2)

(3)

式中:s为特征线段编号;l为特征线段长度;s=p,p+1,…,q为长特线从起点p到终点q穿过的所有特征线段。

长特征线上的源可在特征线扫描过程中计算得到,然后可构造低阶的基于特征线法的加速方程。长特征线上的角通量为:

(4)

网格标通量用穿过网格的所有长特征线平均角通量修正为:

(5)

式中:φ为网格标通量,上角括号为迭代次数,0为启动长特征线加速的初始值,n为跳出加速时的迭代结果;I(M,K)为穿过网格i的所有角度方向的特征线段。

长特征线源用其穿过的所有网格源来修正为:

(6)

式中,Q为网格内的源。长特征线加速方法的计算流程如图2所示。Smith[13]基于轻水堆1/4堆芯二维问题研究了长特征线方法的加速效果,在迭代步上得到了20～50倍的加速效果。长特征线加速方法是一种非线性加速方法,本质上是对输运方程特征法的低阶近似,具有良好的稳定性,因此可以用于扩散非线性加速方法发散时问题的加速。长特征线加速方法的缺点是计算量要明显高于其他加速方法,加速方程求解过于耗时导致其在时间上的加速效果弱于迭代步上的加速效果。

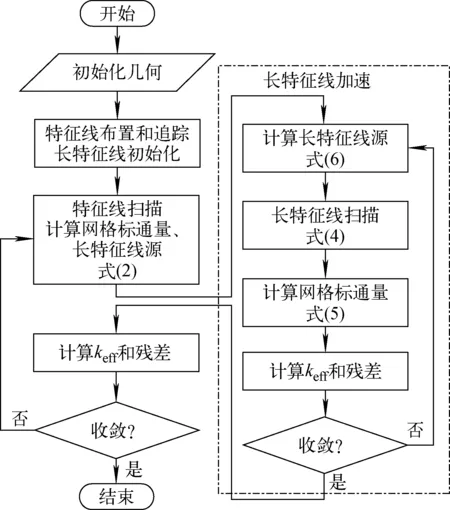
图2 长特征线加速方法计算流程Fig.2 Flow chart of macro-track transport acceleration method

2 稀疏条数长特征线加速方法

为了解决长特征线加速方法计算量大的问题,二维方法中通常采用稀疏角度的方式。二维特征线法将角度方向划分为M个方位角和P个极角,总的方向数为MP,方位角按照等角度间隔的方式划分,极角有多种划分方式,包括:等角度、等权重和TY求积组[14]等。三维特征线法一般采用旋转对称的求积组,常用的求积组有Carlson求积组和Lee求机组等[15]。图3对比了二维和三维特征线法求积组的不同,可以看出二维方法中求积方向在两极相对稠密,因此二维特征线法可以选择具有反射对称性的少量几个方位角和1个极角作为加速方程的求解方向,此时的网格标通量计算公式为:

a——二维特征线法求积组,16个方位角,6个极角;b——三维特征线法旋转对称求积组,S8图3 二维和三维特征线法的求积组对比Fig.3 Comparison of quadrature set for 2-D and 3-D method of characteristics

(7)

三维问题相比二维问题特征线数量高一个数量级,本文提出了稀疏条数长特征线加速方法来降低三维加速方法的计算量,并引入了条数稀疏度概念,如图4所示。三维几何中,按照每t个相邻特征线取一的方式选择用于求解加速方程的特征线,这里的t即为条数稀疏度,此时网格标通量的计算公式为:

a——特征线方法,M=12;b——稀疏角度长特征线加速方法,M=4;c——稀疏条数长特征线加速方法,M=12,t=3图4 长特征线布置方法Fig.4 Macro-track arrangement method

(8)

采用稀疏条数长特征线加速方法相比稀疏角度的优点是不会降低加速方程在角度离散上的精度。一维离散纵标法可以证明,SN阶方程的精度相当于PN-1阶,对于二维和三维问题虽然不能得到相同的结论,但求积方向越多方程的精度越高仍然成立。稀疏条数长特征线加速方法不降低特征线方向数,只在空间上减少特征线的数量,由于三维几何特征线布置相对二维几何是非常稠密的,减少特征线数量不会明显影响式(8)特征线数量积分的准确性。

3 加速方法参数选取

条数稀疏度、长特征线长度和长特征线迭代步是影响加速效果的主要因素。本文基于小型轻水堆基准题对长特征线加速方法的加速效果进行了分析。小型轻水堆基准题[16]是一个边长为50 cm的正方体,计算模型划分为50×50×50个边长为1 cm的正方体小网格,三维特征线间距为0.2 cm,长特征线最大长度限制为2 cm,每次启动加速方法迭代50步后退出。在进行加速参数研究前对特征线间距进行敏感性分析以避免特征线布置的疏密影响加速效果,计算结果如图5所示,有效增殖因数keff偏差为相对特征线间距为0.05 cm时的keff计算结果,可以看出keff偏差随着特征线间距降低而趋于稳定,本文特征线间距是根据keff偏差小于5 pcm的原则选取的。

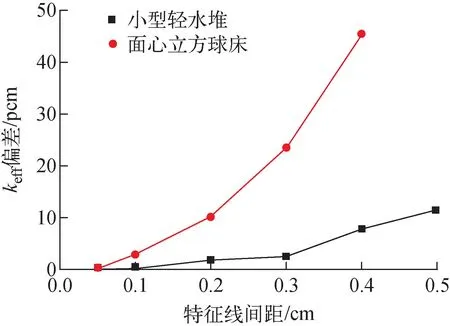
图5 keff偏差随特征线间距变化Fig.5 keff difference variation with track spacing

条数稀疏度对加速效果的影响如表1所列,条数稀疏度为1时的总扫描时间(包括特征线扫描和长特征线扫描)增加了接近1倍,简单计算可以得到长特征线每次扫描所需时间与特征线扫描所需时间相当。条数稀疏度不大于5时,随着条数稀疏度增加总扫描时间快速降低,迭代步和加速迭代步均不变,条数稀疏度进一步变大时加速效果开始出现明显减弱,迭代步和加速迭代步也大幅度增加。说明条数稀疏度大于5时,由于长特征线数量减少,式(8)的计算准确度会严重偏离真实情况。

表1 长特征线加速方法加速效果随条数稀疏度的变化Table 1 Macro-track transport acceleration performance with respect to sparsity

长特征线长度对加速效果的影响如表2所列,计算过程过中条数稀疏度为3,长特征线长度越长单次扫描所需时间越短,长特征线长度越长则低阶加速方程相比特征线方程近似越多,需要的迭代步越多,总的加速效果由以上两个方面因素共同决定,表现为总扫描时间先缩短后增加。

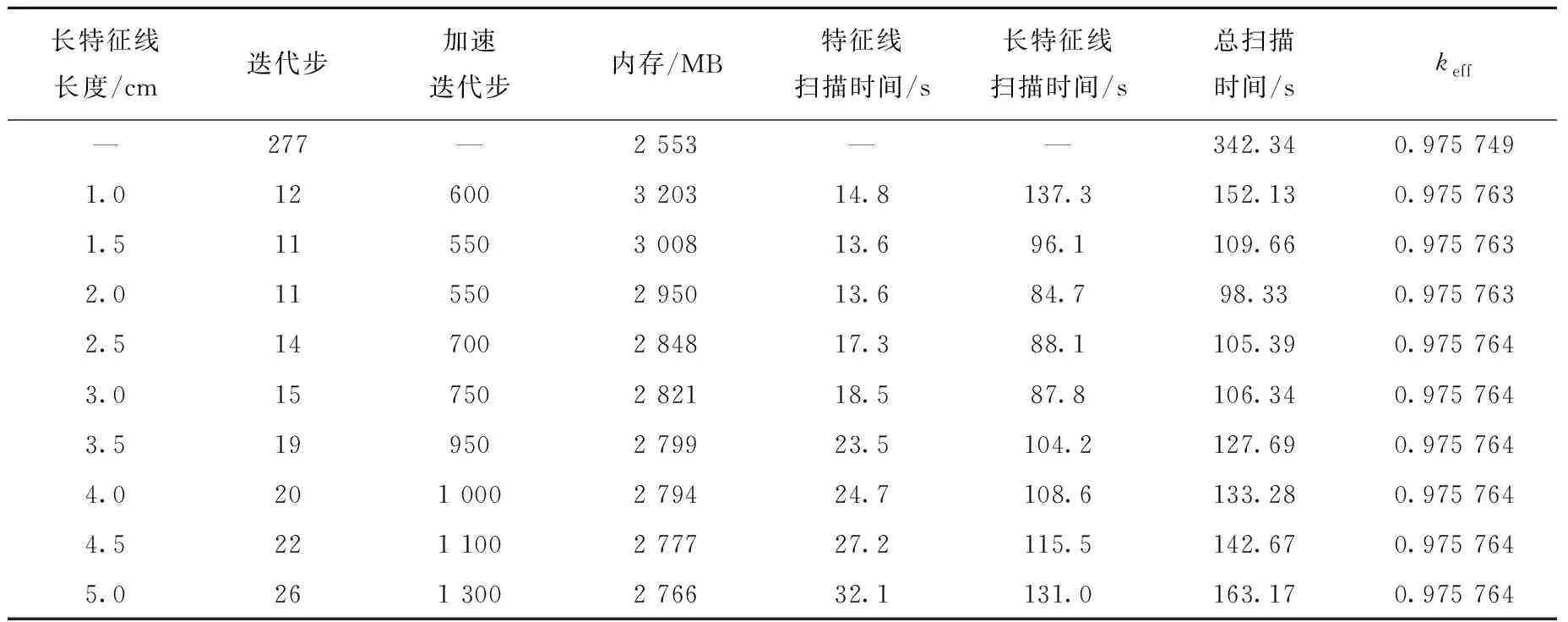
表2 长特征线加速方法加速效果随长特征线长度的变化Table 2 Macro-track transport acceleration performance with respect to length of macro-track

长特征线迭代步用来控制每次启动加速方法后的迭代次数。长特征线迭代步对加速效果的影响如表3所列,计算过程中条数稀疏度为3,长特征线长度为2.0 cm。长特征线迭代步不大于60步时,迭代步随长特征线迭代步增加而降低,之后即使进一步增加长特征线迭代步,迭代步也保持不变。总扫描时间的最小值未出现在长特征线迭代步为60步时,而是出现在20步时,原因是总的扫描时间中长特征线扫描占很大一部分,长特征线迭代步的增多抵消了迭代步的降低。

表3 长特征线加速方法加速效果随长特征线迭代步的变化Table 3 Macro-track transport acceleration performance with respect to macro-track iteration step

综合以上分析,条数稀疏度取3～5,长特征线长度取2.0 cm左右,长特征线迭代步取20～60步时可以获得比较好的加速效果。使用最佳参数时,三维长特征线加速方法在计算时间上可以获得7倍左右的加速效果,此时在迭代步上可以获得20倍左右的加速效果;只考虑迭代步最多时可以得到25倍的加速效果,与二维方法迭代步加速效果基本一致。

4 球床几何加速效果

使用球床几何模型对稀疏条数长特征线加速方法的加速效果进行了验证,受限于服务器的计算能力,构造了1个由172个面心立方堆积的燃料球的简化模型,如图6所示,模型边长为60 cm,中心有一个边长为31.46 cm的正方形空腔区域,燃料球半径为3 cm,球床区域填充率为0.625,三维特征线间距为0.1 cm。燃料球使用小型轻水堆基准题堆芯截面[16],反射层使用小型轻水堆基准题反射层截面,燃料球间隙为空腔,蒙特卡罗程序计算得到的keff=0.843 10(0.00 016)。

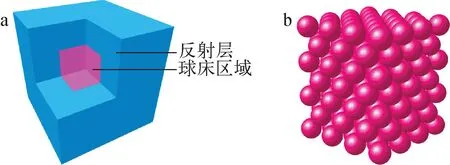
a——正方形球床几何模型;b——球床区域燃料球堆积模型图6 三维面心立方规则堆积球床计算模型Fig.6 Calculation model of 3-D pebble-bed geometry with face-centered regularly packing pebble

计算结果如表4所列,计算过程中长特征线迭代步固定为50步,重点研究了条数稀疏度和长特征线长度对加速效果的影响。从计算结果可以看出,使用稀疏条数长特征线加速后,迭代步可以获得最多30多倍的加速效果,特征线追踪时间可以获得最多7倍左右的加速效果,此时迭代步加速效果为20倍左右。三维面心立方堆积球床的计算证明稀疏条数长特征线加速方法在包含空腔的非规则几何中同样可以获得比较好的加速效果。

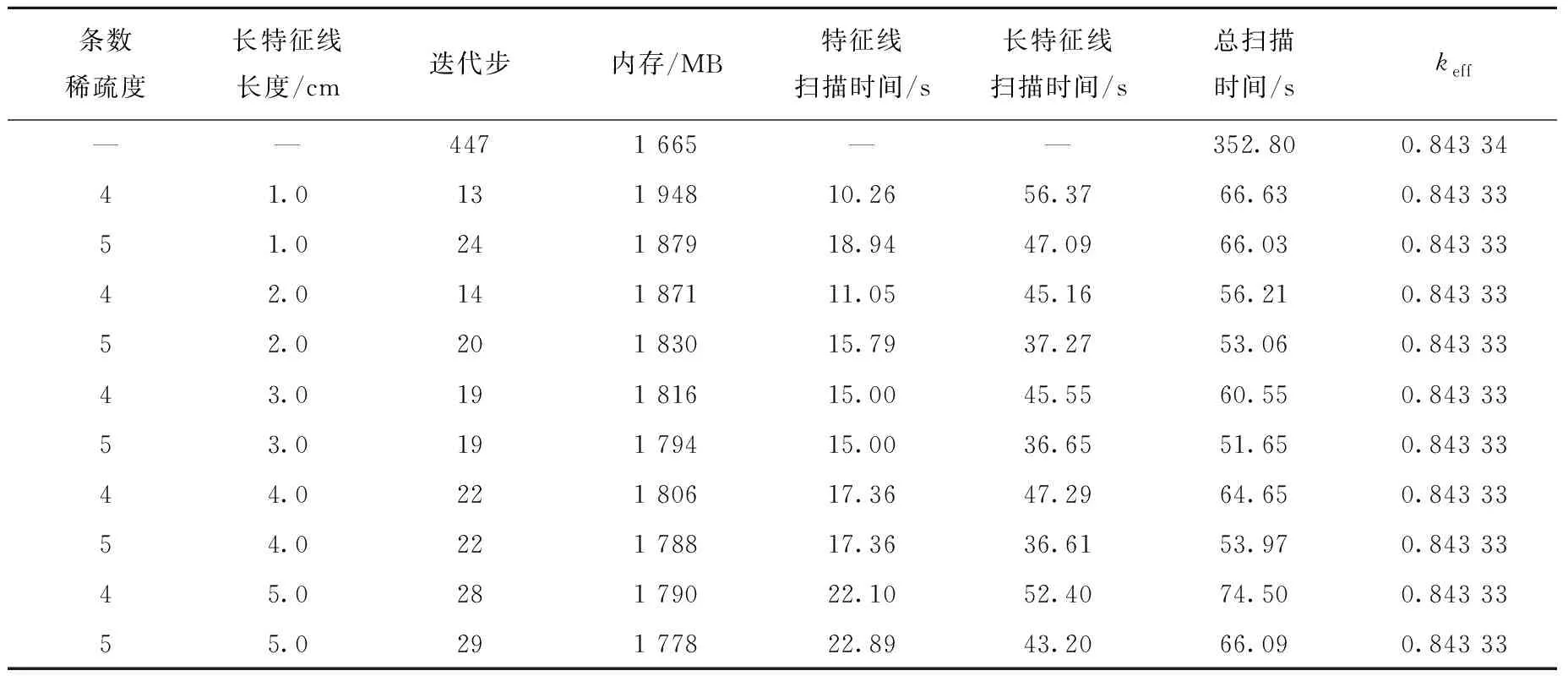
表4 长特征线加速方法对三维球床几何的加速效果Table 4 Macro-track transport acceleration performance in 3-D pebble-bed geometry

5 结论

为解决球床高温气冷堆三维特征线全堆芯输运问题的几何复杂性和迭代速度慢的问题,本文采用长特征线加速方法进行了加速研究,主要结论如下。

1) 将长特征线加速方法应用于三维非规则球床几何并提出了稀疏条数长特征线加速方法,极大地降低了加速方法的计算时间,显著改善了加速效果。

2) 稀疏条数长特征线加速方法在三维非规则球床几何扫描时间上可以获得7倍左右的加速,此时迭代步上可以获得20倍左右的加速,仅考虑迭代步时最多可以得到30多倍的加速效果,总体来说迭代步加速效果与二维特征线法相近。

3) 通过基准题研究,得到了所测试球床问题加速参数的选取范围。条数稀疏度取3～5、长特征线长度取2.0 cm左右、长特征线迭代步取20～60步时可以获得比较好的加速效果。