基于连续能量蒙特卡罗的快中子反应堆均匀化截面计算方法研究

郭 辉,沈宇阳,吴逸炜,陈萃岚,宋去非,顾汉洋

(上海交通大学 核科学与工程学院,上海 200240)

快中子反应堆能有效提高铀资源利用效率、减少高放废物并有助于稳定核燃料循环,是第四代核能系统技术的重要组成部分,也是我国重点发展的先进堆型之一。截至目前,国内外共建造了近20台各型快堆,积累了400余堆年的运行经验。高效准确的反应堆物理分析方法对新型核能系统的研发至关重要。新设计的涌现与精度要求的提高,对快堆的物理计算方法提出了新的挑战,如复杂结构的精确模拟、宽能谱和非均匀效应下的截面生成及高性能大规模并行计算等[1]。蒙特卡罗方法基于精细几何和连续能量数据库,具有较高的计算精度。但对于优化设计、燃料管理、瞬态计算及多物理耦合等任务,其对计算资源要求高的问题尤其显著。快堆确定论两步法通常由组件均匀化截面计算和堆芯扩散/输运计算共同组成,具有较高的计算精度和效率,已广泛应用于快堆工程设计与分析领域。但由于采用空间均匀化、能量分群和角度离散的数值方法,新型设计的复杂结构与能谱必须在均匀化截面生成中精确计算。

在中子能谱上,快堆中子能量主要位于keV～MeV区间,该能量区域共振现象复杂,非弹性散射与(n,xn)等阈能反应重要性增加。在空间上,快堆中子自由程长,堆芯空间耦合紧密。总体空间自屏效应弱,但吸收体等局部结构非均匀性强。快堆中子泄漏强且呈现明显的各向异性。针对这些快堆物理计算的特点,国内外对快堆堆芯用均匀化截面开展了广泛的研究。MC2-3、CONSYST、SARAX-TULIP、ERANOS-ECCO等零维、一维或准二维截面计算程序在传统快堆中已得到广泛验证与应用。为提高燃料组件内非均匀结构与控制棒等复杂组件的计算精度,二维特征线(MOC)方法受到广泛关注,如Guo等[2]在APOLLO3程序、Wei等[3]在SARAX程序中的研究。Faure等[4]基于APOLLO3进一步开发了三维特征线生成截面方法,试图解决ASTRID-CFV等非均匀堆芯的均匀化截面生成问题,但其共振计算能力、计算效率和几何处理能力有待提高。近年来,利用连续能量蒙特卡罗计算均匀化截面受到广泛关注,Nikitin等[5]、Lin等[6]、Tran等[7]、Nguyen等[8]、Martin等[9]、Guo等[10]对蒙特卡罗生成快堆用截面开展了研究。蒙特卡罗方法可建立二维/三维组件与超组件乃至三维全堆模型生成均匀化截面,以充分考虑快堆长中子自由程引起的结构相互作用,精确处理局部复杂能谱变化。已有结果表明,蒙特卡罗产生均匀化截面与堆芯扩散计算结合具有良好的计算效率与精度,但需结合修正技术以提高控制棒等强吸收体的计算精度。Lin等[6]与Guo等[10]的研究表明,基于蒙特卡罗体积通量均匀化方法与堆芯输运计算结合会高估堆芯反应性,需要发展适用于堆芯输运计算的蒙特卡罗生成均匀化截面技术。

本文聚焦基于连续能量蒙特卡罗的快堆均匀化截面计算方法研究。首先,简要梳理国内外蒙特卡罗生成快堆均匀化截面的研究进展;然后,介绍蒙特卡罗生成快堆均匀化截面的基础理论模型,包括体积通量均匀化方法和针对堆芯扩散计算的超级均匀化等效修正方法(SPH),并提出针对堆芯输运计算的蒙特卡罗通量矩均匀化方法(MHT);最后,基于1 000 MWth金属燃料钠冷快堆进行数值验证与分析。

1 国内外研究现状

通过蒙特卡罗方法生成的均匀化截面与多群堆芯计算结合的结果列于表1,其中主要包括Serpent/DYN3D[5]、Serpent/VARIANT[6]、MCS/RAST[7-8]、MCS/MCS(MG)[8]、Serpent/Griffin[9]、OpenMC/TRIVAC[11]、OpenMC/OpenMC(MG)[12-14]。验证与应用算例的堆芯功率涵盖65～3 600 MWth,冷却剂涵盖钠与铅铋,燃料涵盖UOX、MOX、金属、碳化物燃料和氮化物燃料。根据表1结果,堆芯求解器类型可分为堆芯扩散求解器和堆芯输运求解器。

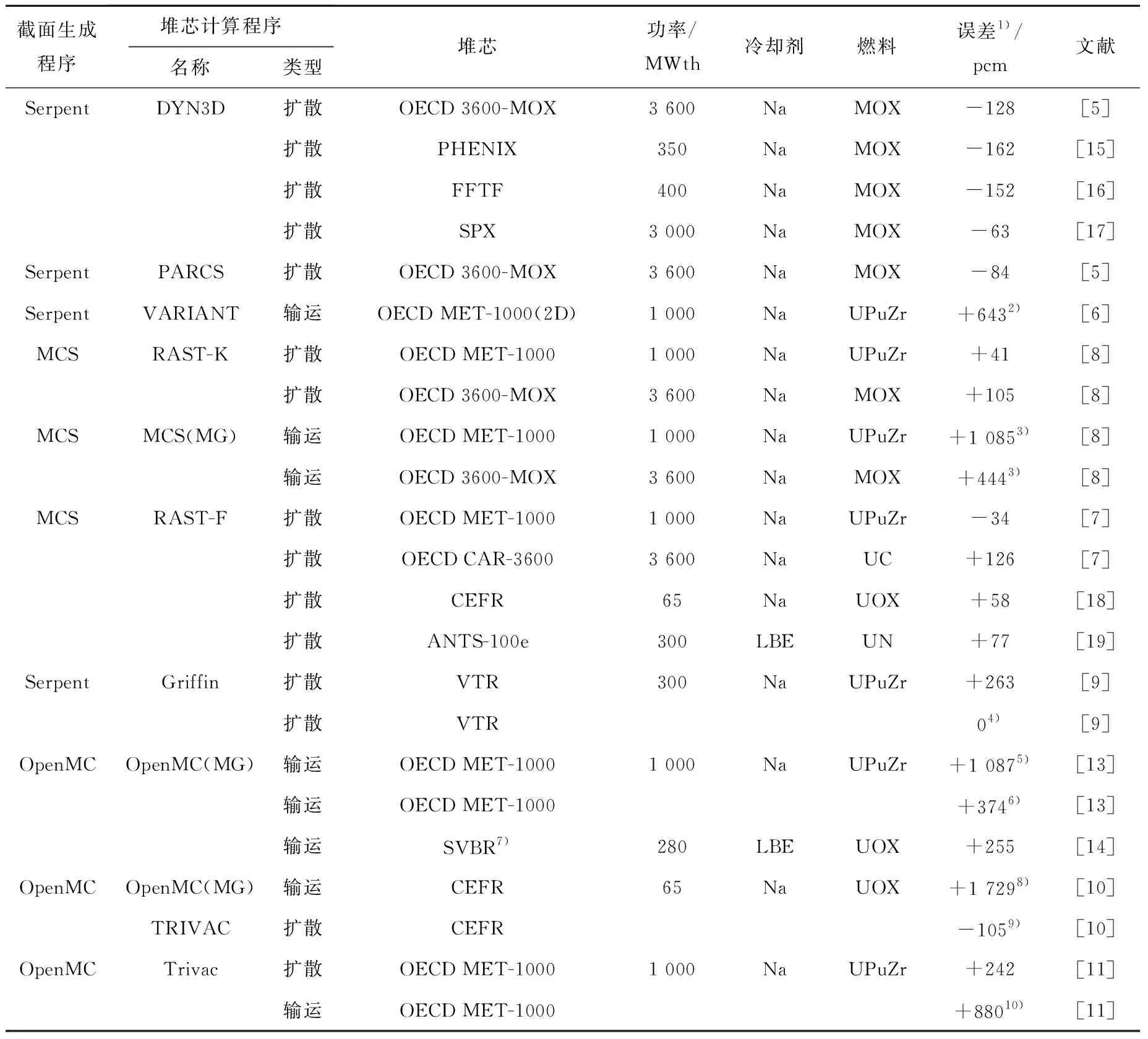
表1 蒙特卡罗生成快堆均匀化截面对堆芯有效增殖因数的计算精度Table 1 Accuracy of Monte Carlo generated multigroup cross-section in predicting core reactivity

1.1 与堆芯扩散计算结合

蒙特卡罗体积通量均匀化方法与堆芯扩散计算结合的两步法所得堆芯有效增殖因数与基准方法之间的偏差在-163～263 pcm之间。对于控制棒未插入堆芯,蒙特卡罗生成均匀化截面与堆芯扩散计算结合的两步法表现出较好的计算精度与计算效率。然而,Nikitin等[5]、Nguyen等[8]、Guo等[11]的结果表明,直接使用该两步法会普遍高估控制棒价值。使用SPH等效修正方法是减小控制棒价值高估的有效方法。

蒙特卡罗法生成均匀化截面在精细几何构建上具有优势。表1中均匀化截面生成模型主要为二维或三维的燃料组件模型、燃料组件与结构组件构成的超组件模型。Serpent/Griffin对MET-1000采用了三维全堆模型,并且对全堆芯截面进行了SPH修正,从而将与基准计算的反应性误差降低到0 pcm。OpenMC/TRIVAC方法对CEFR堆芯采用了三维全堆模型和全堆芯SPH修正,从而将与实验的反应性误差降低到-105 pcm,该误差主要为核数据库引起的误差[20]。全堆SPH等效修正方法在微型反应堆等强非均匀堆芯中亦可应用[21-22]。全堆SPH方法可为特定堆芯计算提供基准群参数,但其产生的截面在不同状态下的鲁棒性还有待进一步验证。

1.2 与堆芯输运计算结合

蒙特卡罗体积通量均匀化方法与堆芯输运计算结合的两步法会明显高估堆芯有效增殖因数。Serpent/VARIANT两步法高估二维OECD MET-1000堆芯反应性约643 pcm。OpenMC/OpenMC(MG)与MCS/MCS(MG)分别高估三维OECD MET-1000堆芯反应性约1 087 pcm和1 085 pcm。OpenMC使用体积通量均匀化方法与DRAGON5-TRIVAC中SP5简化球谐函数输运计算结合高估三维OECD MET-1000堆芯反应性约880 pcm。因此,需要发展针对堆芯输运计算的均匀化方法提高其计算精度。蒙特卡罗通量矩均匀化方法生成截面可将OpenMC/OpenMC(MG)对三维OECD MET-1000堆芯反应性的高估从1 087 pcm降到374 pcm。

2 理论模型

2.1 蒙特卡罗体积通量均匀化方法

蒙特卡罗体积通量法均匀化截面计算方法已得到广泛发展,如SERPENT[23]、MCNP6[24]、McCARD[25]、RMC[26]、JMCT[27]、OpenMC[28]、MCS[7-8]与MCX[29]等。本文以开源蒙特卡罗程序OpenMC[28]中的体积通量法均匀化截面计算方法为例,简要介绍其均匀化截面计算方法[30],不同程序在一些细节上会略有区别。

1) 0阶截面

蒙特卡罗体积通量法中0阶宏观截面定义如下:

(1)

〈Σx,i,φ〉k,g=

(2)

(3)

其中:x为反应类型,如总截面、吸收截面、裂变截面与有效裂变中子数等;i为核素;k为空间区域;g为能群;〈Σx,i,φ〉k,g和〈φ〉k,g为蒙特卡罗计数的反应率和标通量,OpenMC中采用径迹长度估计。

2) 散射矩阵

OpenMC中可通过勒让德多项式或直方分布的形式来表示散射矩阵。勒让德多项式形式较为通用,其l阶散射矩阵计算如下:

(4)

σs(r,E′→E,Ω′·Ω)ψ(r,E′,Ω′)

(5)

其中,〈Σsl,φ〉k,g′→g和〈φ〉k,g采用解析估计进行计数。总截面等采用径迹长度估计,而高阶散射反应率难以采用径迹长度估计。为保持反应率的一致,OpenMC中可采用“一致性”散射矩阵:

Σsl,i,k,g′→g=Σs,i,k,gPsl,i,k,g′→g

(6)

其中:Σs,i,k,g为总散射截面,可由式(1)通过径迹长度估计求得;Psl,i,k,g′→g为散射概率矩阵,可通过解析估计进行计算。

(7)

3) 输运修正

输运截面(Σtr)和输运修正的散射矩阵(Σstr),简称TCP0截面,对减小扩散方程求解的误差具有重要作用。OpenMC中采用限流近似方法进行输运修正:

(8)

Σstr,i,k,g′→g=

(9)

其中,δg,g′为克罗内克函数。

扩散系数由下式计算:

(10)

严格意义上,扩散系数可用过累积徙动方法(CMM)[31-35]获得。CMM可消除由于输运修正近似引起的误差,其对水堆的适应性已得到验证[31-34]。

2.2 超级均匀化等效修正方法

超级均匀化等效修正方法(SPH)[36-37]已广泛用于保持基准非均匀计算与均匀计算间的反应率守恒。在诸多文献[7-8,11,38-39]中,SPH修正已应用于提高蒙特卡罗生成均匀化截面与堆芯扩散计算结合的计算精度。SPH等效修正法的主要流程如图1所示。

图1 超级均匀化等效修正因子计算流程[11]Fig.1 Iteration scheme of SPH[11]

首先,用基准非均匀模型计算均匀化截面,同时存储非均匀体系下的中子通量。蒙特卡罗方法可基于连续能量和精细几何进行组件、超组件及全堆芯模型的基准非均匀计算。

其次,基于以上所得均匀化截面,进行多群、均匀化堆芯计算,获得均匀化通量。

再次,可获得均匀化区域r、能群g的SPH等效修正因子:

(11)

(12)

然后,使用SPH等效修正因子修正截面,计算公式如下:

(13)

最后,将修正后的截面重新代入均匀化多群堆芯计算,获得新的均匀化通量,产生新的SPH等效修正因子与修正截面,往复循环,直至收敛。

SPH等效修正方法属于定点迭代方法,仅需进行一次计算资源要求较高的基准计算,在计算均匀化截面的同时存储对应中子通量数据即可,从而有效降低超级均匀化等效修正所需的计算资源。

2.3 蒙特卡罗通量矩均匀化方法

通量矩均匀化方法在确定论程序APOLLO3的MOC快堆均匀化截面生成模块中得到发展,并应用于快堆分析[41],用于处理总截面随入射角的各向异性,普适于一般的堆芯输运求解器。结合蒙特卡罗生成均匀化截面特点,本文提出了蒙特卡罗通量矩均匀化方法,以下是其简要推导过程。

稳态波尔茨曼方程可写为:

L(r,Ω)+T(r,Ω)=S(r,Ω)+F(r,Ω)

(14)

其中:L为泄漏;T为总反应;S为散射;F为裂变。

如假设截面不随入射角的变化,即通量可分假设或P一致性假设,采用球谐函数表达为:

(15)

(16)

该假设普遍应用于确定论堆芯输运求解器,有效减小了计算量。然而,在材料不连续而引起通量角度强相关的情况下将导致误差。若考虑总截面的角度相关性,准确的方程应写为:

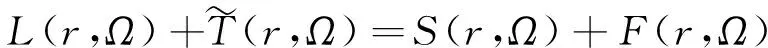
(17)

入射角相关的总截面亦用球谐函数加以考虑:

(18)

为了保证所生成的截面形式在多数堆芯求解器中可用,保持总截面不随入射角变化。

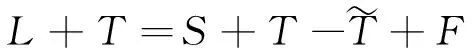
(19)

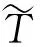
(20)

因此,等效的散射矩阵为:

(21)

以上散射矩阵通用性仍较低,因此Vidal等[41]提出了基于最小二乘法的归并方法,最终等效的散射矩阵为:

(22)

(23)

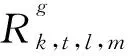
由上述推导可知,MHT的基本原理是将总截面随入射角的各项异性归并入散射矩阵中。从而在考虑截面各项异性的同时,保持所生成总截面在堆芯输运求解器中的泛用性。

2.4 方法讨论

蒙特卡罗体积通量均匀化方法在许多蒙特卡罗程序中均有实现,超级均匀化等效修正方法在蒙特卡罗均匀化生成均匀化截面中已有应用。本文关键技术在于将通量矩均匀化方法与蒙特卡罗生成均匀化截面方法相结合,从而在通用截面形式下考虑截面随入射角的各向异性。需要特别指出的是,本文工作较为局限,蒙特卡罗生成快堆均匀化截面还有许多问题需要深入研究,如不连续因子修正、基模修正、历史效应处理方法等。不连续因子可保证净流守恒,从而改善堆芯有效增殖因数和功率分布计算精度,蒙特卡罗生成不连续因子方法有待研究。基模修正理论可调整计算对象的泄漏率,从而使用考虑泄漏的燃料组件渐进能谱分布并修正群常数,在RMC[42]、Serpent[23]等蒙特卡罗程序中已有研究。快堆均匀化截面历史效应处理方法还需进一步考虑,已有蒙特卡罗程序基于核素微观截面,以燃耗深度和温度为参数,可有效处理压水堆的燃耗历史效应问题[43]。

3 数值验证与分析

3.1 MET-1000基准题

本文采用OECD/NEA/WPRS快堆数值对标[44]中的金属燃料钠冷快堆MET-1000作为对标算例验证以上均匀化截面计算方法。MET-1000堆芯模型如图2所示,该堆芯由72个内燃料组件、102个外燃料组件、114个反射组件、66个屏蔽组件和19个控制棒组件组成。在OECD/NEA/WPRS报告中,有7个组织使用20种不同的计算方法对MET-1000寿期初与寿期末的有效倍增因子、钠空泡值、多普勒常数等关键堆芯参数进行了数值对标。近年来,该算例得到了更加广泛的研究与应用。MET-1000算例基于先进金属燃料快堆,有较详实的参数描述与广泛的研究,因此本文数值验证与分析基于MET-1000开展。

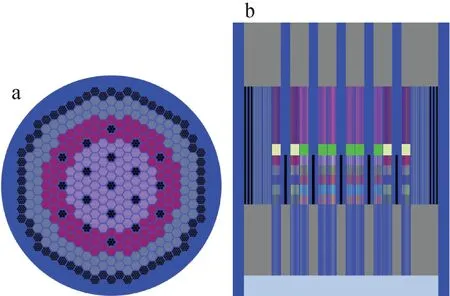
a——径向;b——轴向图2 MET-1000堆芯示意图Fig.2 Layout of MET-1000 core

本文利用OpenMC程序,基于三维全堆MET-1000模型计算其均匀化截面。堆芯计算分别采用DRAGON程序[45]中的TRIVAC扩散求解模块[46]和OpenMC程序中的多群输运计算模式[47]。TRIVAC是DRAGON程序包的堆芯求解模块,包括基于扩散理论的Raviart-Thomas(RT)混合对偶有限元法和简化球谐函数节块法,本文采用其中的扩散求解器。同时,针对蒙特卡罗生成均匀化截面与堆芯扩散计算结合,生成SPH等效修正因子。多群蒙特卡罗方法是假设较少的堆芯输运计算方法,因此本文采用OpenMC的多群模式作为多群输运计算基准。针对蒙特卡罗生成均匀化截面与堆芯输运计算结合,使用了MHT技术。

3.2 与堆芯扩散计算结合

在无控制棒插入时,连续能量精细几何蒙特卡罗计算所得有效增殖因数为1.029 07±0.000 40,堆芯扩散计算所得有效增殖因数为1.031 63,偏差为+242 pcm。控制棒积分价值如图3所示,若无SPH等效修正,堆芯扩散计算方法(TCP0/Diffusion)明显高估了控制棒价值,高估随控制棒插入逐步增加到完全插入时的+2 487 pcm,高估约为控制棒总价值的+13.5%。若对控制棒含吸收体部分的均匀化截面采用SPH等效修正方法(TCP0+SPH/Diffusion),随着控制棒的插入其价值误差在-141～74 pcm之间变化。在控制棒完全插入时,TCP0+SPH/Diffusion对价值预测较好,误差比例仅为+0.35%。但在控制棒微插入时,控制棒价值较小,堆芯计算误差可导致较大控制棒价值误差比例,此时应考虑对相应位置燃料及其他结构物也采用SPH等效修正。

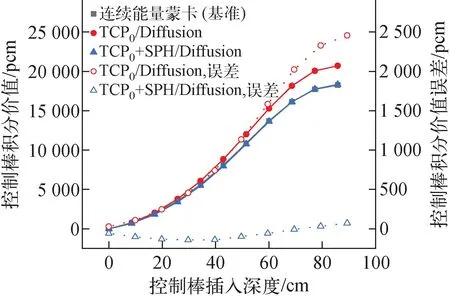
图3 控制棒积分曲线Fig.3 S-curve of control rods

三维功率误差最大值与最小值随控制棒插入深度的变化如图4所示,可见,SPH等效修正提高了功率预测的准确性。在控制棒未插入时,无SPH等效修正的三维功率分布与连续能量蒙特卡罗对比,误差在-4.4%～+3.2%之间,主要误差原因为控制棒吸收能力被高估导致堆芯顶部功率被低估,而堆芯底部功率被高估。经过SPH修正后,三维功率分布的误差减小到-2.3%～2.2%之间,且误差的空间分布更加均匀。随着控制棒的移动,无SPH等效修正的局部功率误差可达-10.5%,而SPH等效修正的局部功率误差始终在-4.2%～+3.0%以内。

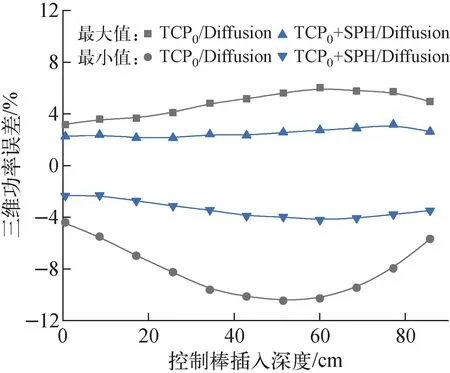
图4 三维功率误差最大值与最小值随控制棒插入深度的变化Fig.4 Variation of relative maximal and minimal error with insertion of control

3.3 与堆芯输运计算结合

对于MET-1000堆芯,OpenMC/OpenMC(MG)计算方法的精度如图5所示。使用体积通量均匀化及3阶勒让德散射矩阵时多群输运计算比基准方法高估1 192 pcm。通过入射角直接离散方法证明了截面随入射角的各向异性是计算误差的主导因素,约772 pcm。入射角直接离散方法难以普适确定论输运求解器。采用2.3节中的MHT,可降低高估约698 pcm。剩余74 pcm可能是MHT均匀化未考虑其他截面类型随入射角的各项异性。

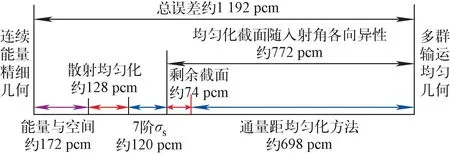
图5 蒙特卡罗生成均匀化截面与堆芯输运计算结合的误差分解Fig.5 Decomposition of reactivity bias of Monte Carlo generated homogenized cross-sections with transport core calculation

在假定散射出射各向同性的系统中,OpenMC/OpenMC(MG)仍高估反应性约938 pcm,证明散射出射角各向异性影响约为254 pcm。将散射矩阵勒让德阶数从3阶提高到7阶,可减小误差120 pcm。通过进一步在多群蒙特卡罗中采用完全非均匀几何以及更加精细的能群结构,可进一步减小误差172 pcm。剩余128 pcm可能是因为蒙特卡罗生成多群截面时在式(5)中使用的不是对应l阶的通量。

功率误差如图6所示。体积通量均匀化方法误差分布不均,趋向于低估内堆芯顶部功率,而高估外堆芯底部功率,误差在-3.63%～+4.02%间。MHT减小功率预测误差,误差在-2.39%～+2.76%之间,且误差分布更加均匀。

图6 蒙特卡罗体积通量(a)和通量距(b)均匀化方法功率误差Fig.6 Power errors without MHT (a) and with MHT (b)

4 结论

连续能量蒙特卡罗方法计算均匀化多群截面方法可精细模拟2D/3D几何,同时可减少共振计算的假设,可适用于复杂几何与能谱,对先进快堆非均匀堆芯的高精度计算具有重要作用,近年来在高性能计算机不断发展的背景下得到广泛研究。本文聚焦使用连续能量蒙特卡罗的快堆均匀化截面计算方法研究。

1) 蒙特卡罗体积通量均匀化方法与堆芯扩散计算结合时,对无强吸收体堆芯计算精度良好。需要通过SPH等效修正方法减小对控制棒价值的高估。SPH等效修正方法亦可实现三维全堆修正,以实现特定堆芯状态点的高精度计算。但SPH修正因子在不同状态点的鲁棒性有待深入研究。

2) 蒙特卡罗体积通量均匀化方法与堆芯输运计算结合时,明显高估堆芯有效增殖因数。对于MET-1000对标算例,通过定量分解分析误差分布,明确了其主要原因是未考虑总截面随入射角的各项异性。MHT将总截面随入射角的各向异性并入散射矩阵中,从而提高了计算精度并普适堆芯输运求解器,为蒙特卡罗生成适用于堆芯输运计算截面提供了一种新的方法。该方法残余误差仍有待进一步消除,在类似ASTRID-CFV等三维强非均匀堆芯中的使用仍有待进一步验证。

蒙特卡罗均匀化截面计算方法在功率分布、反馈系数、扰动状态和计算效率等方面的特性仍需深入研究。其在强非均匀先进快堆和小型快堆方面的误差与改进方法有待系统性研究。