函数展开计数在CLUTCH方法中的初步应用

黄金龙,曹良志,贺清明,秦 帅,吴宏春

(西安交通大学 核科学与技术学院,陕西 西安 710049)

核数据是核反应堆中子学计算的重要输入参数,其敏感性分析结果可反映对响应参数敏感的核数据,进而对核反应堆堆芯设计和不确定度量化[1]等有重要的指导意义。反复裂变几率(IFP)方法[2]被众多蒙特卡罗程序用于k特征值对核数据的敏感性分析[3-6],该方法的主要缺点是,内存占用与每代模拟粒子数呈正比,当每代模拟粒子数较大时,内存占用甚至不可接受。Kiedrowski在MCNP中提出稀疏矩阵[7]存储方式,以降低IFP方法的内存使用。数据表明,采用稀疏矩阵方法可降低10～100倍的内存,但内存占用量依旧较大。Perfetti[8]提出CLUTCH方法[9-10]可在不损失结果精度的前提下,显著降低内存占用。CLUTCH方法需要划分网格来统计权重函数,且网格的大小[8]推荐为1 cm3,对于大规模问题(如压水堆全堆问题),需要划分大量网格来统计权重函数,在网格数量较多的情况下,保证权重函数收敛所需的粒子数是不可接受的。因此,本文将使用函数展开计数(FET)方法[11]对权重函数进行统计,提高统计权重函数的精度和效率,从而实现对大规模问题的高效率、高精度的连续能量核数据敏感性分析。

本文在蒙特卡罗程序NECP-MCX[12]上实现基于网格和函数展开计数方法的CLUTCH方法(CLUTCH-Mesh和CLUTCH-FET),以进行k特征值对核数据敏感性分析。以IFP方法[13]的计算结果为参考解,在Godiva、Flattop和AP1000全堆问题上对CLUTCH-Mesh和CLUTCH-FET方法进行验证,并比较两种方法的计算精度和效率。

1 理论方法

基于一阶微扰理论,k特征值对核数据的灵敏度系数S可表示为:

Sk,Σx(r,E)=

(1)

其中:Σx(r,E)为x反应道在位置r处能量为E的宏观截面;F为裂变项算子;S为散射项算子;T为碰撞项算子;ψ为中子通量;ψ*为共轭通量;〈,〉表示在相空间中积分。

由式(1)可看出,灵敏度系数是反应率和共轭通量的乘积,反应率在蒙特卡罗计数中容易统计,共轭通量可用IFP和CLUTCH方法求解。

1.1 CLUTCH方法

基于Contributon理论[14],相空间中某点P0处的共轭通量表达式为:

(2)

其中:Qs(P0)为粒子进入P0时的权重;χ(r,E)为r处出射能量为E的裂变谱;ν(E′)为入射能量为E′的裂变中子数;Σf(r,E′)为位置r处能量为E′的裂变截面;Ω′和Ω分别为中子的入射方向和出射方向;ψ(r,Ω′,E′|P0)为从P0点产生的中子在(r,Ω′,E′)处产生的中子通量;G(P0→r)为转移函数,表示从P0处转移到r处的中子通量;I*(r)为r处的权重函数。

权重函数I*(r)可根据未归一的裂变谱的灵敏度系数求解,表达式为:

(3)

其中:D为式(1)的分母项;式(3)的分母表示初始代r处产生的裂变中子数,分子表示初始代由r处产生的裂变中子,经过几个蒙特卡罗代的模拟后,在渐近代产生的中子数,因此,I*(r)为初始代r处平均产生的1个裂变中子在渐近代所产生的中子数。由于I*(r)只与空间位置有关,因此,通常基于空间网格对I*(r)进行统计且可在非活跃代统计得到。空间网格需要足够精细,以准确描述权重函数的空间分布,同时需要模拟足够多的粒子,以保证权重函数收敛。Perfetti[8]推荐,网格大小约为1 cm3,每个包含燃料的网格有1 000个非活跃代中子历史,可保证权重函数足够精细和收敛。以AP1000全堆问题为例,为保证网格大小约为1 cm3,需采用320×320×400的网格,为保证每个包含燃料的网格有1 000个非活跃代中子历史,若每代模拟的中子数为106,则需要模拟的非活跃代数为28 581代,计算代价很大。因此,本文将使用函数展开计数方法对权重函数进行统计。

1.2 函数展开计数方法

1) FET系数求解

蒙特卡罗统计目标量φ(ξ)可用任意正交完备的基函数展开[11],表示为:

(4)

其中:ξ为归一化后的相空间位置;n为函数展开阶数;an为n阶函数展开系数;φn为n阶展开函数;ρ(ξ)为ξ处的权重函数。

根据基函数的正交性,可求解an:

(5)

其中,Γ为正交区域。

基于碰撞估计器,可得到an的估计表达式:

(6)

基于函数展开计数方法对式(3)进行统计时需分两步:1) 初始代用函数展开计数方法统计裂变中子的分布,即统计分母,并保存函数展开系数;2) 由于初始代的裂变中子分布已得到,即式(3)的分母已知,再用函数展开计数方法对式(3)进行统计。

2) 勒让德多项式

勒让德多项式[15]是在区间[-1,1]上的正交多项式,n阶勒让德多项式可表示为:

(7)

其在区间[-1,1]上的正交性表示为:

(8)

以基于勒让德函数对三维空间变量φ(x,y,z)的函数展开为例进行说明。φ(x,y,z)可表示为:

(9)

其中:i,j,k分别为x,y,z方向展开系数索引;I,J,K分别为x,y,z方向展开阶数;fi,j,k为函数展开系数,根据式(8)所示勒让德函数的正交性,fi,j,k可根据式(10)求得。

(10)

基于碰撞估计器,可得到fi,j,k的估计式:

(11)

在非活跃代基于勒让德多项式对权重函数进行函数展开计数,将得到的各阶展开系数代入式(9),在活跃代即可得到空间各位置处的权重函数,将得到的权重函数代入式(2),用于共轭通量的求解,进而由式(1)计算得到灵敏度系数。

2 数值结果

基于上述理论方法在NECP-MCX中实现基于网格和函数展开计数的CLUTCH方法,用于k特征值对核数据的敏感性分析,并与IFP方法的计算结果比较,对比CLUTCH-Mesh和CLUTCH-FET方法的计算精度以及效率,其中计算效率用品质因子(FOM)衡量,品质因子的定义如式(12)所示。

(12)

其中:R为蒙特卡罗统计量的相对统计标准差;T为蒙特卡罗计算时间。品质因子越大,则计算效率越高。本文选取Godiva、Flattop和AP1000全堆问题进行验证,使用ACE格式的ENDF/BⅦ.0数据库。

2.1 Godiva问题

Godiva基准题[16]是一个均匀裸球装置,材料为高浓铀,半径为8.741 cm,如图1所示。灵敏度系数计算采用2 000个蒙特卡罗代,其中活跃代设为1 000代,每代模拟粒子数为105,块的大小设置为10代。由于Godiva属于一维问题,因此只需在半径方向上对权重函数进行统计。

图1 Godiva基准题Fig.1 Model for Godiva problem

选用不同展开阶数的勒让德多项式对权重函数进行统计,得到不同展开阶数下CLUTCH-FET方法计算的灵敏度系数,如表1所列,其中Ave和RSD分别为灵敏度系数均值和相对统计涨落。

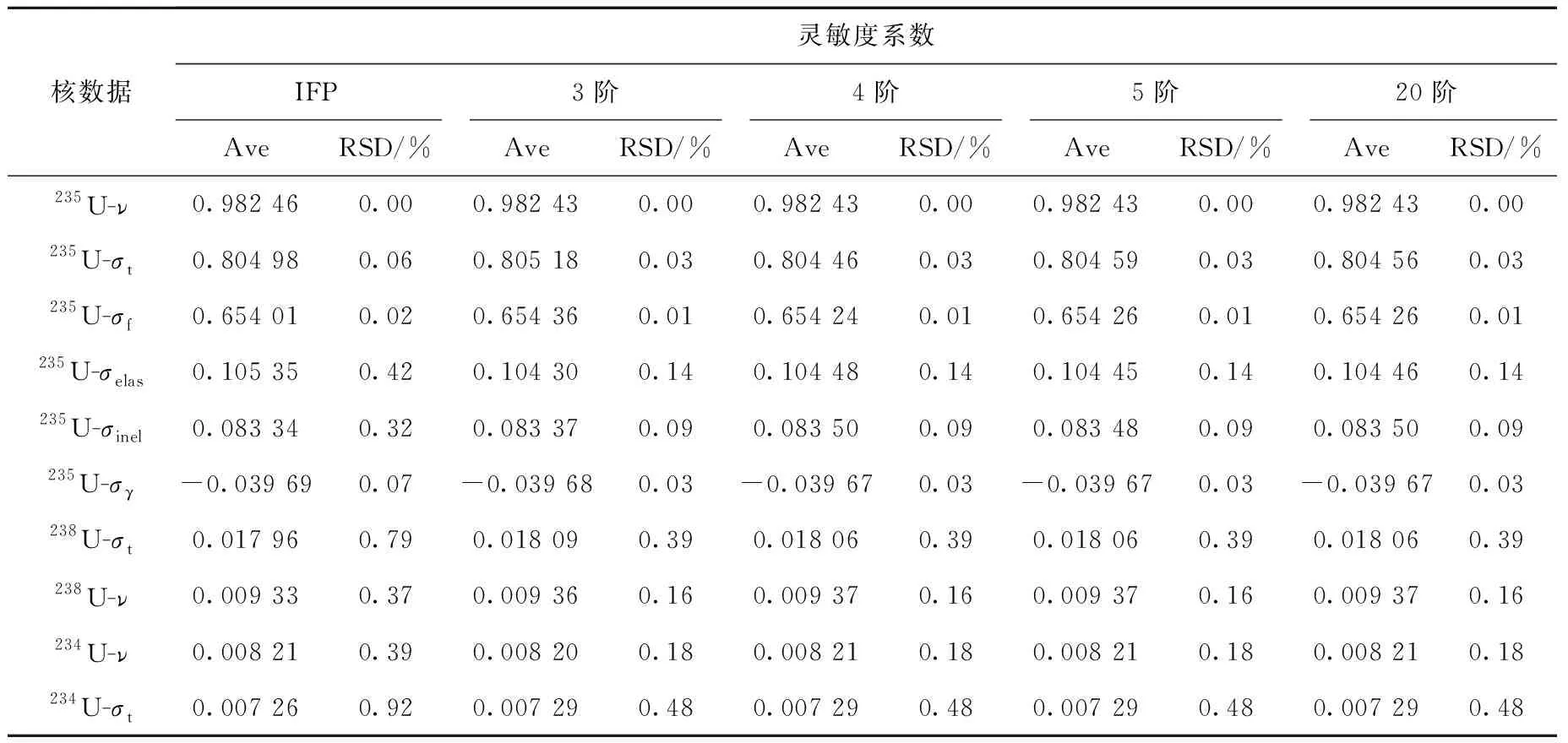
表1 Godiva问题中不同展开阶数下CLUTCH-FET方法计算的灵敏度系数Table 1 Sensitivity coefficient of CLUTCH-FET method under different expansion orders for Godiva problem

(13)

其中:m为反应道序号;M为反应道总数,即M=10;dn,m为勒让德阶数取n阶时第m个反应道的灵敏度系数计算结果与参考解之间的差异,表示为:

(14)

其中:Aven,m和RSDn,m分别为展开系数阶数取n的第m个反应道的灵敏度系数的均值和相对统计涨落;AveIFP,m和RSDIFP,m分别为IFP方法的第m个反应道的灵敏度系数的均值和相对统计涨落。

图2 Godiva问题中不同展开阶数下CLUTCH-FET方法计算的灵敏度系数与参考解间的差异Fig.2 Difference between sensitivity coefficients calculated by CLUTCH-FET under different expansion orders and reference for Godiva problem

CLUTCH-Mesh方法在半径方向上划分16等分作为统计权重函数的网格。CLUTCH-FET方法采用4阶勒让德多项式对权重函数在半径方向上的分布进行统计,两种方法求得的权重函数分布如图3所示,IFP、CLUTCH-Mesh和CLUTCH-FET方法计算得到的灵敏度系数列于表2,FOM值示于图4。

表2 Godiva问题灵敏度系数计算结果Table 2 Sensitivity coefficient result for Godiva problem

图3 Godiva问题权重函数分布Fig.3 Distribution of importance weighting functions for Godiva problem

图4 Godiva问题FOM值对比Fig.4 Comparison of FOM values for Godiva problem

图3表明,基于网格和基于函数展开计数方法计算得到的权重函数符合得较好,随着半径的增大,权重函数的数值逐渐减小。表2显示,CLUTCH-Mesh和CLUTCH-FET方法的计算结果与IFP方法计算结果的相对偏差基本小于1%,表明了两种方法的准确性。通过对比图4所示FOM值,可看出, CLUTCH-Mesh和CLUTCH-FET方法计算得到的灵敏度系数的FOM值相近,CLUTCH-Mesh方法计算得到的FOM值略高于CLUTCH-FET方法,两种CLUTCH方法的FOM值普遍高于IFP方法,表明CLUTCH-Mesh和CLUTCH-FET方法相比于IFP方法计算效率有较大提升。同一方法、不同核数据的FOM值也有较大差异,这与不同反应道发生的概率有关。

2.2 Flattop问题

Flattop基准题[16]布置如图5所示,装置中心材料是钚合金,反射层材料是铀,堆芯半径为4.533 2 cm,反射层外径为24.142 cm。CLUTCH-Mesh方法采用半径方向均分48份一维球状网格,CLUTCH-FET方法在半径方向上全局和分段进行函数展开计数,其中全局函数展开计数表示在半径方向上对[0 cm,24.142 cm]进行勒让德函数展开,展开阶数分别取5、10、15、20阶,分段函数展开计数表示在半径方向上分别对[0 cm,4.533 2 cm]和[4.533 2 cm,24.142 cm]进行勒让德函数展开,得到两套函数展开系数,展开阶数均为4阶,其他计算参数与Godiva问题相同。得到的权重函数沿半径的分布如图6所示,3种方法计算的灵敏度系数列于表3,FOM值示于图7。

表3 Flattop问题灵敏度系数计算结果Table 3 Sensitivity coefficient result for Flattop problem

图5 Flattop基准题Fig.5 Model for Flattop problem

图6 Flattop问题权重函数分布Fig.6 Distribution of importance weighting functions for Flattop problem

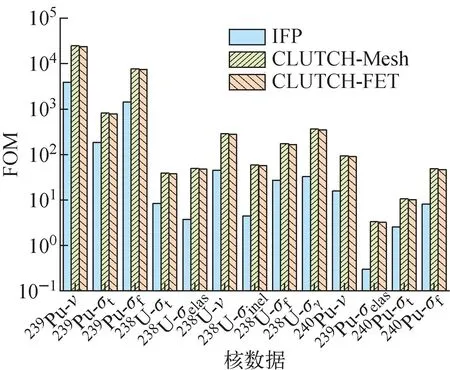
图7 Flattop问题FOM值对比Fig.7 Comparison of FOM values for Flattop problem

图6表明,权重函数在半径方向上的变化达到上百倍,若不进行分段函数展开计数,展开阶数取20阶,仍无法准确统计出权重函数的分布,因此需要进行分段函数展开计数,才能较好地拟合权重函数的分布。结果显示,分两段进行函数展开计数,展开阶数取4阶时,便可得到较好的权重函数分布结果。因此,当权重函数变化较大时,分段进行函数展开计数较全局函数展开计数的效果更好。一般函数展开计数的分段选在材料分界处,保证每段函数展开计数区域内权重函数的梯度不大,以得到更精确的权重函数。图6还表明,分段进行权重函数展开计数时,在区间边界处会出现间断,但由于权重函数仅在燃料区域有意义,且研究结果[8]表明灵敏度系数的计算对权重函数的精度要求为10%～20%,因此权重函数在区间边界处的间断性对灵敏度系数的计算影响较小。由表3可看出,基于CLUTCH-Mesh方法和CLUTCH-FET方法计算的灵敏度系数与IFP结果的相对偏差均小于1%,且两种方法的计算偏差数值相近,表明两种方法具有较高的精度且精度相近。图7表明,基于CLUTCH-Mesh方法和CLUTCH-FET方法计算得到的灵敏度系数的FOM值相近,且普遍高于IFP方法的FOM值,表明两种CLUTCH方法的计算效率比IFP方法更高。

2.3 AP1000全堆问题

AP1000堆芯布置如图8所示,采用15×15的燃料布置,共157个燃料组件,控制棒处于全提状态。在统计权重函数时,CLUTCH-Mesh方法采用340×340×400的立方体网格,以保证网格的大小约为1 cm3,CLUTCH-FET方法对每个燃料组件分别进行函数展开计数,即采用157套函数展开计数,每个燃料组件内,x、y方向各选取4阶勒让德函数展开计数,由于燃料区域的材料在z方向没有变化,因此在z方向不分段,由于z方向燃料区域较长,适当选取高阶展开系数,选取10阶勒让德函数展开计数。每代模拟的粒子数为106,其他计算参数同Godiva问题。IFP、CLUTCH-Mesh和CLUTCH-FET方法计算的灵敏度系数列于表4,FOM值对比示于图9。

表4 AP1000全堆问题灵敏度系数计算结果Table 4 Sensitivity coefficient result for AP1000 problem

图8 AP1000堆芯布置Fig.8 AP1000 core layout

图9 AP1000问题FOM值对比Fig.9 Comparison of FOM values for AP1000 problem

表4表明,在当前计算条件下,CLUTCH-Mesh方法计算得到的238U-σγ、1H-σelas、10B-σt、235U-σγ和1H-σγ的灵敏度系数的计算相对偏差较大,均大于1%,1H-σγ的甚至达到-3.04%,这是由于AP1000全堆问题规模较大,需要划分足够精细的网格才能准确描述权重函数的空间分布,网格数的增多使得每个网格统计得到收敛的权重函数所需的粒子数增多,根据前文结果,在当前网格设置下,每代模拟106个粒子,需要28 581代的非活跃代模拟才能使权重函数收敛,而本次计算仅采用1 000代非活跃代,权重函数未收敛,导致灵敏度系数的计算相对偏差较大。而在当前计算条件设置下,CLUTCH-FET方法计算得到的灵敏度系数的相对偏差均小于1%,表明CLUTCH-FET方法具有较高的精度。对比图9所示的FOM值,发现CLUTCH-FET方法的FOM值普遍高于CLUTCH-Mesh和IFP方法,CLUTCH-Mesh方法的FOM值最低,这是由于CLUTCH-Mesh方法中网格数达到千万级别,对于数据量在千万级别的数组进行规约和运算非常耗时,导致CLUTCH-Mesh方法的FOM值比CLUTCH-FET方法小。相较于IFP方法和CLUTCH-Mesh方法,CLUTCH-FET方法的FOM值分别最大提高了5.2倍和6.0倍。

3 结论

本文分别基于网格和函数展开计数方法对CLUTCH方法中的权重函数进行了统计,函数展开计数选取的基函数为勒让德多项式,在Godiva、Flattop和AP1000全堆问题上进行了验证,并将两种CLUTCH方法(CLUTCH-Mesh和CLUTCH-FET)计算得到的灵敏度系数与IFP方法进行了比较。结果表明,对于Godiva和Flattop问题,CLUTCH-Mesh和CLUTCH-FET方法具有和IFP方法相当的精度,且相较于IFP方法,两种CLUTCH方法的计算效率有显著提升。对于AP1000全堆问题,因该问题规模较大,统计权重函数所需的网格数较多,导致权重函数难收敛,从而使得CLUTCH-Mesh方法的计算精度下降,表明CLUTCH-Mesh方法不适用于大规模问题的灵敏度系数求解。而在选取合适的函数展开阶数的条件下,CLUTCH-FET方法的计算精度与IFP方法相当,计算效率有所提升,其品质因子较IFP方法最大提高了5.2倍,较CLUTCH-Mesh方法最大提高了6.0倍,表明CLUTCH-FET方法适用于大规模问题的灵敏度系数求解。Flattop问题的权重函数分布结果表明,分段进行函数展开计数的效果较不分段的效果好。