点探测器敏感性关联抽样计算方法

李 瑞,付元光,邓 力,许海波

(1.中物院高性能数值模拟软件中心,北京 100088;2.北京应用物理与计算数学研究所,北京 100094)

在反应堆辐射屏蔽设计中,常需要通过改变屏蔽体尺寸、材料密度与组分实现屏蔽方案的优化。在此过程中,掌握这些因素导致的辐射剂量率变化规律可有效提高屏蔽方案优化效率。另外,核数据本身的不确定性会对辐射屏蔽模拟结果的准确性造成影响,在屏蔽方案的评估中也需要加以考虑。当不同屏蔽方案的差异较小时,上述计算辐射剂量率变化的问题可视为微扰问题。

反应堆辐射屏蔽模拟一般采用离散纵标(SN)方法与蒙特卡罗(MC)方法。其中SN方法属于确定论方法,在计算微扰问题时可直接采用两次独立计算并做差的方式进行。但是,由于SN方法对于复杂几何处理能力有限,并存在射线效应等问题,其计算精度一般低于MC方法。与SN方法相比,MC方法可处理比较复杂的几何体,采用的连续能量核反应截面也更适用于核数据扰动分析。但MC方法的计算量巨大,特别是对于辐射屏蔽这一类深穿透问题,需要使用降方差技巧才能得到统计收敛结果。然而,在微扰问题计算中,由于辐射剂量率本身的改变就很小,如果采用直接MC模拟方法计算,则对于其统计收敛性要求更加苛刻,导致时间开销进一步增加。因此,为排除随机涨落的影响,MC方法一般在与参考系统相同的随机序列下完成微扰系统的模拟,常见的方法包括关联抽样[1]与微分算符[2]。

近年来,采用伴随通量作为重要性的降方差技巧在MC辐射屏蔽模拟中被广泛研究,如针对单一目标的CADIS算法[3]以及多目标的FW-CADIS算法[4]。这些算法的实质是基于粒子权重的赌/分裂以及偏倚抽样的组合。另一方面,在MC辐射屏蔽模拟中,常采用点探测器计数方法提高计数率。

MCNP软件[5]基于微分算符法,提供了体平均通量及其衍生计数的敏感性计算功能。Perel等[6]在此基础上研究了点探测器计数的敏感性计算方法。与体平均通量这一类径迹长度估计方法不同,点探测器计数采用了下次事件估计方法[7],需要额外考虑虚粒子的模拟过程。在Perel等[6]展示的算法中,需多次遍历粒子的径迹历史贡献。在采用权重赌/分裂技巧的屏蔽问题模拟中,次级粒子的数目很多且平均粒子随机游动链较长,这种算法的性能开销会很大。本工作基于关联抽样算法架构,利用单因素扰动系统将系统扰动因素局限在可通过一个扰动权重描述的简单情形,在此基础上以随输运过程实时更新的方式代替频繁的粒子历史遍历。另外,将扰动权作为粒子扩展属性也可避免对次级粒子径迹的回溯需求,从而降低算法的实现难度。

1 算法介绍

关联抽样算法的重点在于采用与原系统相同的随机序列模拟扰动系统的输运与计数统计过程。在形式上,扰动系统粒子随机游动过程与原系统是完全相同的,统计差异仅体现在粒子权重上。本工作基于三维粒子输运模拟软件JMCT开展算法研究[8]。

对于辐射屏蔽问题,点探测器计数估计量[6]可表示为:

(1)

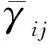
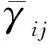
(2)

式中:δ为克罗内克函数,表示仅当虚粒子飞行方向朝向点探测器时触发计数;Ωd为虚粒子飞行方向矢量;Rd为点探测器的位置矢量;R为随机游动链中粒子的位置矢量;Ps为粒子发生反应时在点探测器方向发射粒子的概率,即指向概率;Σt为总反应截面;s为虚粒子到达探测器过程中经历的径迹段长度。

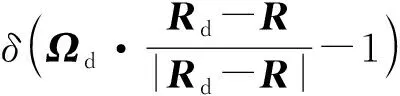
式(1)中的Pik(Ek)为粒子随机游动链中径迹段的产生概率,按照Perel等[6]对于径迹段指标的约定,每个径迹段以碰撞或源抽样事件开始,因此点探测器计数是在径迹段开始处触发的。由于虚粒子与实际碰撞或源抽样过程是独立的,因此影响第k个径迹段点探测器计数的所有径迹段k∈lin(j)并不包括k径迹段本身[6]。因此,对于首个点探测器计数,仅依赖径迹段0,为保证形式上的一致性,将径迹段指标定义进行简单扩展,扩展之后的径迹段概率为:

(3)

Q为辐射屏蔽计算中的外源分布,源粒子的位置属性指标为0,能量与方向指标为1。由于粒子从R0飞行到R1过程中,其能量与方向是不变的,因此E1与Ω1分别对应了第2个径迹段开始之前粒子的能量与飞行方向。对于k>1的情况,位置属性指标与径迹段的关系以此类推。

T为输运核,表示粒子飞行至下一次碰撞的概率,其形式为:

T(Rk,Ek,Ωk;Rk-1)=

(4)

Cx为各类反应的碰撞核,如式(5)所示。

Cx(Rk-1,Ek,Ωk;Ek-1,Ωk-1)=

(5)

式中:Σt为宏观总截面;Σx为宏观反应截面;νx为反应发生后产生的次级粒子数目,主要用于中子诱发裂变、(n,xn)以及中子产光等反应过程。

(6)

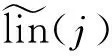
(7)

式(6)所示为权重技巧下的点探测器计数形式。当系统存在扰动时,基于关联抽样计算点探测器计数对应变化量Δ(Td)的过程为:

Δ(Td)=Est*[Td]-Est[Td]=

(8)

式中,上标*表示扰动系统相关项。

式(8)对应的随机游动过程与式(6)类似,唯一的区别就是引入了扰动权乘子

(9)

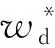
(10)

(11)

根据式(8)～(11)可构建点探测器扰动量的关联抽样算法。仅需要在原系统随机游动模拟过程中更新并统计扰动权对应的计数即可,算法流程如图1所示。

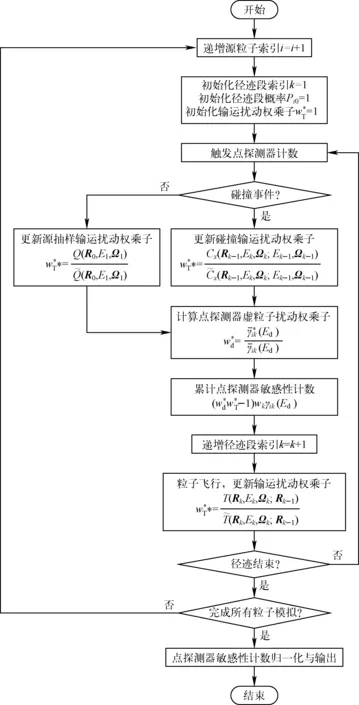
图1 点探测器扰动关联抽样计算流程Fig.1 Flowchart of point detector perturbation based on correlated sampling

另一方面,为完成点探测器扰动的模拟,对于每一个扰动因素,都需要建立与原系统结构相同的统计计数。结构相同是指点探测器的数目、能量区间划分、时间区间划分都相同。具有相同结构的扰动系统计数可通过对原系统计数进行克隆得到。所有扰动系统克隆计数的总内存使用量M如式(12)所示。

(12)

式中:Np为扰动系统总数;Nd为点探测器计数数目;Mi为每个点探测器计数的内存使用量。

JMCT中允许在一次模拟中同时分析多个扰动因素,这些扰动因素包括核素截面与材料密度的变化,以及针对扰动因素的能量区间划分。在本工作中,将某一能量区间内具有单一核素与反应道扰动或材料密度扰动的系统定义为单因素扰动系统。因此,一次MC模拟过程中,可存在多个单因素扰动系统。扰动系统对应的计数内存与内部状态是独占的,有效地避免了不同扰动因素在计算流程上相互干扰。对于每个单因素扰动系统,可通过扩展固定数目为1的粒子属性即可完成输运扰动权乘子的管理。此外,JMCT允许定义扰动所在几何体与材料,从而限制扰动的空间范围。

2 计算结果

利用劳伦斯利弗莫尔国家实验室(Lawrence Livermore National Laboratory, LLNL)的脉冲球形实验装置对算法进行正确性检验。该实验探测D-T脉冲中子在半径为20.96 cm的石墨球中输运后的时间泄漏谱,装置如图2所示。其中D-T中子源发生器通过孔道经-x方向放置于x=-0.131 cm处。D-T中子能量介于13.20～15.11 MeV区间内,具体分布依赖于出射角度。实验中,NE-213探测器与-x轴呈30°角,距离石墨球心776 cm。文献[9]给出了该模型相应的MCNP程序[5]输入文件。

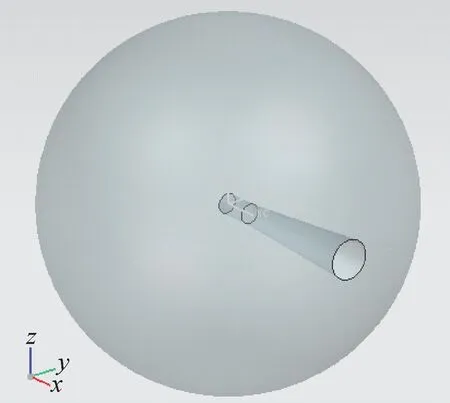
图2 脉冲球形实验装置模型Fig.2 Model of pulsed sphere experiment device

JMCT首先基于该模型进行了泄漏谱的计算,作为对比的实验值来自文献[10]。JMCT整体计算结果与Perel等[6]工作符合良好,如图3所示。

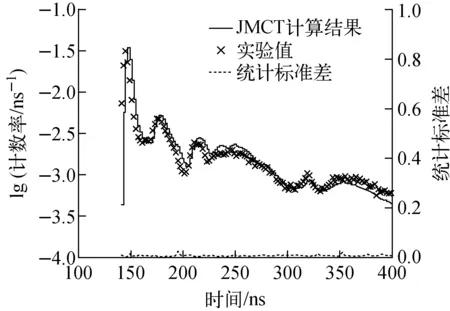
图3 脉冲球形实验装置时间泄漏谱计算结果Fig.3 Calculation result of time leakage spectrum for pulsed sphere experiment device

在此基础上,对14.918～15.296 MeV区间内的(n,n′1)反应截面引入+1%的扰动,计算时间谱的变化。由于该实验装置中D-T中子在石墨球中平均运行2.9个自由程,因此扰动引起的时间泄漏谱变化主要集中在0～2次散射对应的时间区间上。JMCT计算结果如图4所示。其中由于(n,n′1)反应截面的增加导致扰动系统的总截面变大,进而造成点探测器直穿项计数降低。另外,散射截面的贡献会由于散射截面的增加而变大,其中一次散射的贡献最为显著。将JMCT点探测器直穿项和一次散射峰的变化与Perel等[6]工作中微分算符计算结果进行定量对比,相对偏差均在5%以内,如表1所列。

表1 时间泄漏谱扰动结果对比Table 1 Comparison of time leakage spectrum perturbation

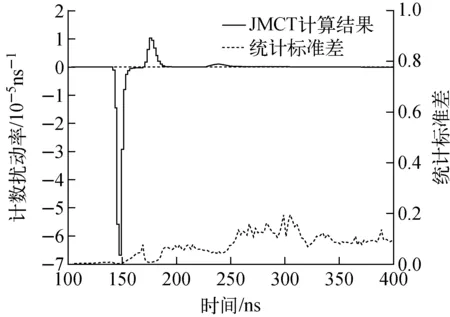
图4 脉冲球形实验装置时间泄漏谱扰动计算结果Fig.4 Calculation result of time leakage spectrum perturbation for pulsed sphere experiment device

针对反应堆辐射屏蔽问题,采用NUREG/CR-6115屏蔽基准题[11]验证使用降方差技巧的点探测器敏感性计算结果。通过在压力容器材料中引入+1%的核子密度扰动,计算压力容器外中子能谱的扰动。为保证计算收敛,该模拟采用了CADIS降方差方法[3],其中伴随通量来自JSNT[12]计算。在4×108粒子历史规模下,JMCT压力容器外表面中子能谱与文献[11]中的DORT结果对比如图5所示。

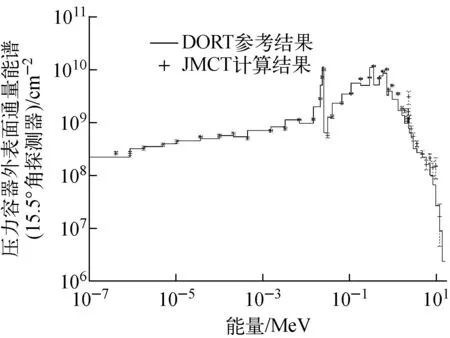
图5 压力容器外表面中子能谱计算结果Fig.5 Calculation result of neutron energy spectrum on outer surface of pressure vessel

这里采用直接MC模拟作为参考对比,关联抽样的计算结果如图6所示。结果表明,两者在趋势上是符合的,即1～2 MeV能量区间的中子通量下降,而1 MeV能量以下的中子通量增加。导致这一现象的原因主要有2个:一方面是由于压力容器材料对快中子的慢化作用导致高能中子慢化为低能中子;另一方面,压力容器内的Fe等核素对快中子的辐射俘获较低能中子更加显著。在该算例中,为避免两次直接MC模拟的统计误差掩盖真实扰动,要求各能群统计标准差均低于0.02,两次MC计算共耗时4 286.2CPU小时,关联抽样计算耗时4.1CPU小时。

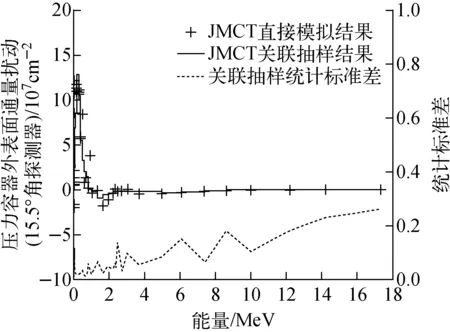
图6 压力容器外表面中子能谱扰动计算结果Fig.6 Calculation result of neutron energy spectrum perturbation on outer surface of pressure vessel

3 结论

脉冲球形实验装置计算结果表明,基于关联抽样的点探测器敏感性计算方法可达到与Perel等[6]工作中微分算符方法相当的计算精度,说明了算法对输运与计数过程的微扰描述是正确的。在NUREG/CR-6115屏蔽基准题模拟中,CADIS降方差技巧的使用一方面对源抽样与输运过程进行了偏倚,另一方面也会在权重轮盘赌过程中产生大量的次级粒子。本工作利用单因素扰动系统的概念将扰动因素进行了规范化,在每个单因素扰动系统内,以粒子扩展属性的方式实现了扰动权乘子的更新。这一方法解决了权重技巧下输运与计数过程的微扰描述问题,并且利用次级粒子的存库与获取顺序避免了敏感性统计中对粒子历史进行频繁的回溯,从而降低了算法的运行时间开销。