基于MOOSE平台液态金属冷却快堆燃料性能分析程序开发

邵世豪,刘宙宇,许晓北,宗育凡,曹良志,吴宏春

(西安交通大学 核科学与技术学院,陕西 西安 710049)

较高的铀资源利用率和较硬的中子能谱等优点使快堆技术成为我国核电“三步走”战略中的重要一步。液态金属冷却快堆作为第四代核能系统极具潜力的堆型之一,对于我国核能创新发展具有非常重要的意义[1]。

燃料元件是核反应堆最基本的部件之一,对其进行的燃料元件性能分析是反应堆研发中最具挑战性的工作之一。燃料元件性能分析用于预测燃料行为与关键参数的演化,是指导燃料元件设计、预测燃料元件服役寿命、确保反应堆安全运行的重要课题之一。国内针对压水堆燃料性能分析程序已经开展了大量研究,然而,相较于压水堆,快堆的运行环境更为严苛,其通量水平更高,运行温度也更高,这导致堆芯材料结构在快堆中受到的辐照影响比压水堆更为显著[2]。因此,开发一套适用于快堆环境的燃料性能分析程序,对于优化快堆设计、提升其安全性以及确保反应堆的长期稳定运行具有至关重要的意义。

从20世纪开始,许多国家相继开发了一系列针对液态金属冷却快堆燃料元件性能分析程序,如美国麻省理工学院(MIT)开发的FEAST-OXIDE[3],适用于氧化物燃料和金属燃料,被认为是目前考虑物理现象最为全面的快堆燃料性能分析程序;法国原子能与可替代能源委员会(CEA)开发的GERMINAL[4]以及日本原子能委员会开发的FEMAXI-FBR[5]等。国内近些年也开发了一些快堆燃料元件性能分析软件,如中国原子能科学研究院开发的LIFEANLS[6],是国内第1个快堆燃料性能分析程序,以及后续开发的FIBER程序[7-8];中国科学技术大学开发的KMC-FUEL[2]等。

为实现快堆燃料元件性能分析程序自主化,本文基于多物理耦合平台MOOSE,开发燃料元件性能分析程序LoongCALF,该程序旨在模拟燃料元件在稳态工况下的长寿期服役性能演化,为LMFR燃料元件设计、服役寿命预测及安全评价提供科学依据。本文首先对LoongCALF程序进行介绍,随后,通过构建并计算两个设计算例,将LoongCALF程序与中国原子能科学研究院开发的Fiber-Oxide程序进行深入对比分析,确保LoongCALF程序的可靠性和有效性,为其在实际应用中的推广使用提供坚实的基础。

1 方法

1.1 程序总体介绍

LoongCALF程序是在之前的轻水堆燃料性能分析程序NECP-CALF[9]的基础上,扩展而来的针对液态金属冷却快堆燃料元件的燃料性能分析程序。程序的体系结构分为4个层次:控制层、求解层、物理层与材料层,如图1所示。其中:控制层负责软件的启动、执行与调度;求解层负责热-力耦合方程的求解;物理层负责燃料中物理现象及过程的模拟;材料层负责计算材料行为参数。

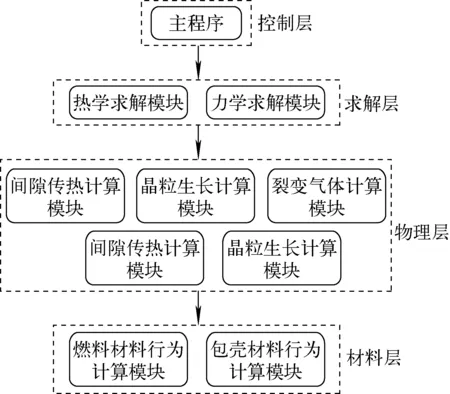
图1 程序体系结构示意图Fig.1 Schematic diagram of program architecture

程序的主要处理流程如图2所示。

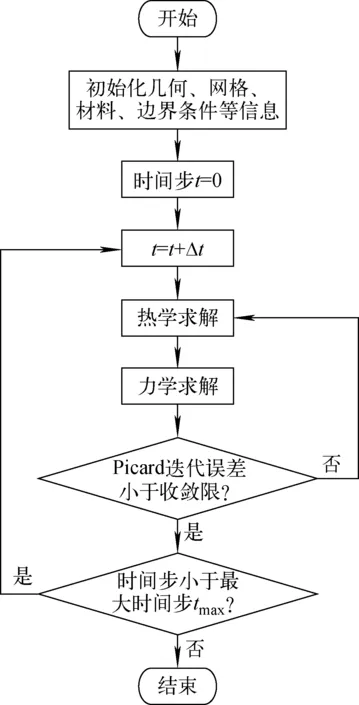
图2 程序主要处理流程图Fig.2 Main processing flowchart of program

在燃料性能分析中,热-力耦合问题涉及温度场和应力场之间的动态交互,这些交互通过材料的热膨胀系数、热传导率等物理参数得以体现。针对这一问题,程序采用Picard迭代方法(又称固定点迭代方法)进行求解。该方法将多物理场问题分解为多个独立的子问题,这些子问题(如温度场、应力场等)通过MOOSE框架中的MultiApp模块进行模拟求解。在求解某个物理场过程中,其他物理场采用初始值或者上一迭代步的计算结果,通过迭代更新耦合物理变量,直至满足预设的收敛条件。Picard迭代方法的应用显著提升了燃料在复杂热力环境下的性能预测的准确性和效率。

对于单独的热学或力学问题求解,JFNK方法(Jacobian-free Newton-Krylov method)已成为一种高效且实用的数值求解策略。该方法巧妙地结合了Newton法的收敛性与Krylov子空间方法的计算效率,同时避免了显式计算或存储完整雅可比矩阵的需求,从而显著降低了计算资源和内存的使用量。然而,为进一步提升JFNK方法的性能和稳定性,通常采用预处理计算方法来优化其求解过程。预处理矩阵的引入旨在改善线性系统的条件数,进而加快迭代收敛速度。在这一过程中,基于MOOSE框架本身的预处理功能,而MOOSE则采用解析表达式来定义预处理矩阵。这种方法不仅提高了求解的精度,还增强了算法的鲁棒性,使得能够更加准确地模拟和预测物理现象。

1.2 基于MOOSE平台程序开发

MOOSE(multiphysics object oriented simulation environment)平台是一个开源的,能够同时模拟多个物理场,用于构建复杂系统的仿真模型。它支持多维度建模计算,可同时模拟多个物理场,如热传导与力学物理场耦合计算。在MOOSE中,可使用模块化的方式来创建复杂的仿真模型,每个模块可代表1个物理场或1个子系统,通过组合这些模块,可构建出多维度、多物理场的仿真模型。此外,MOOSE还提供了丰富的物理模型库,包括常见的材料模型、边界条件、初始条件等,方便用户快速构建仿真模型。

表1 燃料元件结构参数Table 1 Structural parameter of fuel element

程序基于MOOSE平台进行开发,充分利用了MOOSE平台的优势。程序采用模块化设计,有单独的材料模块,目前燃料类型支持UO2及MOX,包壳材料支持HT9及1515Ti,冷却剂材料支持钠、铅及铅铋。此外程序还具备向316(Ti)SS、T92等先进包壳材料及U-Zr、U-Pu-Zr金属燃料扩展的架构条件。

为满足不同复杂度和需求的模型计算,程序为用户提供了多种建模方式和多维度网格求解功能。建模方式包括可视化建模和基于脚本的数字化建模两种方式。可视化建模方式直观易用,用户可通过简单的拖拽和配置即可完成模型的构建;而基于脚本的数字化建模方式则更加灵活,用户可通过编写脚本来自定义模型和计算流程。此外,程序支持一维、二维和三维网格建模计算,以满足不同尺寸和形状的燃料元件模型构建需求。目前,对于燃料元件建模,程序通常采用1.5维建模方法。这种方式不仅大幅减少了计算网格的数量和复杂度,简化了模型构建和维护过程,还降低了对计算资源和时间的需求。同时,它依然能够捕捉燃料行为的关键特征,为分析提供有效的支持。

1.3 数学模型

1) 控制方程

燃料元件的温度通过热传导方程求解:

(1)

式中:ρ为密度,kg/m3;cp为比热,J/(kg·℃);T为温度,K;k为热导率;S为热源。

燃料元件的应力-应变状态通过固体力学平衡方程求解:

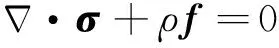
(2)

式中:σ为应力;f为单位质量的体积力。

几何方程为:

(3)

式中:ε为应变;u为位移,m。

本构方程为:

σ=E:(ε-εplastic-εcreep-εeigen)

(4)

式中:E为弹性张量;εplastic为塑性应变;εcreep为蠕变应变;εeigen为本征应变。

2) 流体换热模型

程序采用单通道假设[2],燃料元件与环绕它的流体通道换热,通道与通道之间没有物质和能量的交流。冷却剂温度控制方程为:

(5)

式中:c为冷却剂比热容,J/(kg·K);T为冷却剂温度,K;w为冷却剂轴向流速,m/s;qv,ch为冷却剂流道中的体积热源,W/m3,包括γ辐射带出的少量沉积在冷却剂区域的裂变能及包壳向冷却剂传递的热量(以体积热源的形式引入)。

3) 裂变气体行为模型

模拟燃料中裂变气体的释放常用的方法为两步法:第1步,裂变气体在晶粒内部产生并扩散到晶界,在晶界处逐渐形成气泡;第2步,裂变气体的气泡在晶界处不断长大、合并,最终与外界气体环境连通,使得储存在晶界中的裂变气体被释放到外界气体环境中[10]。

第1阶段的气体扩散过程由下式描述[11]:

(6)

式中:Cg为晶内裂变气体浓度;t为时间;Deff为有效气体扩散系数;r为一维球坐标系的坐标;β为气体产生速率。

第2阶段,当晶界气体与外界连通(即晶界气体达到饱和)时,其在晶界上的面浓度由下式计算:

(7)

f(θdihe)=1-1.5cosθdihe+0.5cos3θdihe

(8)

式中:Ns为裂变气体在晶界上的饱和面浓度,m-2;rb为晶界处裂变气体气泡半径,m;θdihe为晶界气泡的二面角;Vc为饱和时晶界被气泡覆盖的比例;kB为玻耳兹曼常数,kB=1.380 6×10-23J/K;γ为气泡表面张力,J/m2;pext为外部静水压力,Pa。

晶界处的裂变气体积攒超过限值时,多余的气体将被释放到燃料元件气腔中。

4) 燃料化学与结构调整

(1) 氧金属比-燃耗依赖关系

燃料中的氧金属比会影响燃耗的速度和程度,通过研究氧金属比与燃耗的相关性,可更准确地预测燃料的燃烧寿命和性能。

氧金属比的计算参考文献[12],即:

(9)

对于VU=4,且VPu<4,有:

(2YBa-Sr+4YZr-Nb+3YY-Re+4fMoYMo)β

(10)

对于VU>4,且VPu=4,有:

(2YBa-Sr+4YZr-Nb+3YY-Re+4fMoYMo)β

(11)

控制燃料的初始氧金属比,使铀的价态在整个辐照循环中不会显著超过4,这将限制燃料包壳化学相互作用(FCCI)。

(2) 孔隙迁移

通常,氧化物燃料中包含了制造过程中形成的孔隙,这些孔隙被氦气所填充。由于这些孔隙体积大且保持低压,因此其形状呈透镜状。当燃料处于运行功率下,这些孔隙会沿着温度梯度向燃料的内部区域迁移。这一迁移机制主要基于蒸汽传输过程:孔隙在热表面发生蒸发,并在冷表面发生冷凝。因此,孔隙会逐渐迁移到燃料棒的中心区域,最终形成一个中心空洞[3]。

孔隙迁移速度按照以下关系式计算:

Vp=0.337 6exp(-66 490/T)

(12)

式中,Vp为孔隙速度,m/s。

孔隙率分布函数Np(r,t)是用于描述孔隙率随时间以及燃料棒中径向位置而变化的数学表达式,具体可由以下方程求解:

(13)

Np(r,t=0)=Np0

(14)

Np(r=R,t)=Np0

(15)

式中:Np0为制造的燃料中的孔隙浓度;Np(r,t=0)描述方程求解的初值;Np(r=R,t)描述方程求解的边界条件。

(3) 晶粒生长模型

在反应堆中,燃料的晶粒会逐渐生长,晶粒的尺寸是裂变气体行为模型中的一个重要参数,晶粒生长模型采用Ainscough等[13]提出,Khoruzhii等[14]修正的晶粒长大动力学[2],即:

(16)

式中:a为晶粒直径,μm;K为晶粒生长率,μm2/h;amax为可稳定存在的晶粒上限尺寸,μm;airr为考虑辐照效应的修正,μm。

5) 材料行为与物性模型

(1) 热导率

MOX燃料热导率由下式计算[3]:

k=F1F2F3F4ko

(17)

(18)

(19)

(20)

(21)

F4=1-αP

(22)

式中:k为MOX燃料热导率;β为燃耗,at%;P为燃料孔隙率;α为孔隙系数(1.5或2.5),本文取α=2.5。

(2) 热膨胀

热膨胀模型对燃料芯块的尺寸变化进行建模。燃料的尺寸变化会影响芯块到包壳的间隙尺寸,这是决定间隙传热的一个主要因素,从而决定储存能量,这是安全分析的一个重要量。MOX燃料的线热膨胀应变模型[3]为:

(23)

式中:ED为缺陷生成能,J;k=1.38×10-23J/K;K1,2,3为模型系数。

(3) 重定位

当核反应堆运行时,芯块会受到高温和高压的作用,导致燃料碎片的热膨胀和震动移位。MOX燃料直径迁移由下式计算:

DR=0.111GDci-45

(24)

式中:DR为直径迁移,μm;G为直径间隙,μm;Dci为包壳内径,mm。

为保证芯块外径与重定位模型计算值一致,令芯块中央空洞也产生重定位应变。重定位应变只产生在R-θ平面上,其线应变为:

εl=DR/2Rpout

(25)

(4) 肿胀

MOX燃料裂变反应产生的裂变产物大部分为固态,小部分为气态,这些产物滞留在燃料中,造成燃料的肿胀。

固态裂变产物导致的肿胀被称为固态肿胀,可由下式[15]计算:

Δεsw-s=5.577×10-5ρΔBu

(26)

式中:Δεsw-s为固态肿胀体应变增量;ρ为密度,kg/m3;ΔBu为燃耗增量。

气态裂变产物导致的肿胀被称为气态肿胀,可由下式计算:

Δεsw-g=1.96×10-31ρΔBu(2 800-T)11.73×

exp(-0.016 2(2 800-T)-0.017 8ρBu)

(27)

式中,Δεsw-g为气态肿胀体应变增量。

(5) 密实化

燃料芯块在服役过程中,随着裂变产物的累积和温度的提升,燃料中的孔隙不断收缩,导致芯块整体的收缩,这样的现象被称为密实化。

MOX燃料密度分数[3]由下式计算:

ρ=ρo+(0.96-ρo)(1-exp(-Bu/0.6))

(28)

式中:ρ为燃料密度分数;ρo为初始燃料密度分数。

密实化导致的应变:

εV=ρo/ρ-1

(29)

(6) 蠕变

燃料芯块及包壳在高温情况下,即使其应力小于材料的屈服极限,也会缓慢地发生不可逆的形变,这种现象叫做蠕变。

MOX燃料热蠕变由下式计算[3]:

(30)

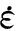
辐照蠕变:

(31)

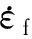
2 程序验证结果

为验证本文开发的液态金属冷却快堆燃料元件性能分析程序LoongCALF的计算准确性及适用性,设计了两个基准算例进行数值模拟与计算。算例1是以UO2为芯块、1515Ti为包壳的燃料棒;算例2是以MOX为芯块、HT9为包壳的燃料棒。Fiber-Oxide程序是由中国原子能科学研究院开发的钠冷快堆燃料元件性能分析程序[7],被选为本文的参考程序。两个算例的燃料元件结构参数列于表1,沿轴向功率分布如图3所示。

图3 轴向功率分布Fig.3 Axial power distribution

使用LoongCALF程序对两个基准算例进行数值模拟与计算,将LoongCALF程序计算得到的芯块最高温度、间隙宽度、应力、气腔压强及裂变气体释放相关参数与Fiber-Oxide程序计算结果进行比较,本文仅展示最大功率的轴向段5的各参数随时间点变化,其他功率轴向段结论相同。

2.1 芯块最高温度对比分析

两个算例轴向段5芯块最高温度比较结果如图4所示。

图4 燃料最高温度比较Fig.4 Comparison of the highest fuel temperature

燃料性能温度分析模块中,芯块包壳间隙宽度对温度产生直接且重大的影响。这种影响主要体现在间隙宽度存在差异的情况下,芯块内表面温度会呈现出显著的差异。此外,芯块热导率模型的差异也是导致温度差异的重要因素。参考文献[16]中各国际知名燃料性能分析程序计算得到的温度差异最大在300 K左右,对于两个算例,两个程序的最大绝对偏差为150 K左右,最大相对偏差为10%以内,在可接受范围之内。

2.2 间隙宽度对比分析

两个算例轴向段5间隙宽度比较结果如图5所示。

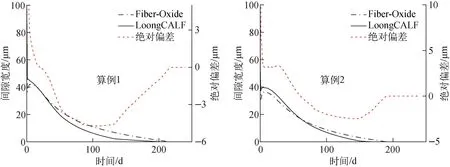
图5 间隙宽度比较Fig.5 Comparison of gap width

间隙宽度的初始差异源于两个程序在处理重定位应变时的理念不同。两个程序对于芯块包壳接触时间预测大致相同,但由于影响芯块包壳间隙的物理量诸多,如热膨胀、肿胀、密实化、蠕变等都会对芯块包壳作用产生应变,不同程序间很难做到完全一致,总体符合较好。

2.3 应力对比分析

两个算例轴向段5包壳内表面米塞斯应力比较结果如图6所示。

图6 包壳内表面米塞斯应力比较Fig.6 Comparison of cladding inner surface Mises stress

包壳应力的不同主要源于两种方法对包壳处理方式的差异。Fiber-Oxide采用了广义平面应变假设,而LoongCALF则采用二维计算方式。但可看到两个程序对应力趋势的预测大致相同,符合较好。

2.4 压强及裂变气体对比分析

两个算例气腔压强及裂变气体释放份额比较结果如图7、8所示。

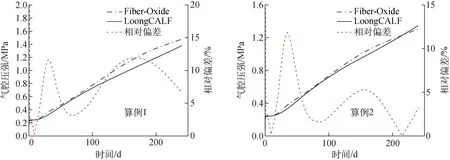
图7 气腔压强比较Fig.7 Comparison of plenum pressure

图8 裂变气体释放份额比较Fig.8 Comparison of fission gas release fraction

气腔压强受裂变气体影响,由于两个程序裂变气体开始释放的时间不同而略有差距。Fiber-Oxide程序计算得到的裂变气体开始释放的燃耗明显早于LoongCALF程序,但考虑到裂变气体释放计算具有较大不确定度以及不同模型之间的差异,这样的结果是可接受的,同时观察到,两个程序对运行后期的裂变气体释放份额模拟基本相同,符合较好。

3 结论

本文开发的快堆燃料元件性能分析程序LoongCALF具备对快堆UO2及MOX燃料的一系列分析功能,包括导热、间隙传热、重结构、裂变产物迁移、裂变气体释放、辐照肿胀、辐照蠕变等计算功能。为验证程序的准确性,本文设计了两个完整燃料棒算例进行程序对比测试。结果表明,LoongCALF程序能够准确模拟液态金属冷却快堆稳态工况条件下燃料元件内部的燃料行为与关键参数演化。

鉴于燃料行为涉及多种复杂现象的耦合,且不同模型间的兼容性对分析结果至关重要,未来将依托更多实际测量案例,对LoongCALF程序进行更深入的验证,以确保其准确性和合理性。同时,程序可基于2.5维和三维建模开展更多的复杂几何工况分析。

本研究得到了中国原子能科学研究院Fiber-Oxide程序结果的帮助,为本研究提供了重要的比较数据。在此,对中国原子能科学研究院的贡献表示衷心的感谢,同时感谢陈启董老师的经验分享与技术指导。