钠冷快堆燃料元件性能分析程序的开发与验证

陈启董,高付海

(中国原子能科学研究院 核工程设计研究所,北京 102413)

从安全角度看,精确预测快堆燃料元件在辐照环境下的演变越来越重要。在燃料元件运行期间,辐照引起的燃料和包壳的热和力学性能的变化非常复杂,因其行为不但取决于制造过程,而且取决于功率水平、功率历史、燃耗等运行因素[1]。预测或评估使用寿命期间的燃料行为的一种有效方法是使用燃料性能分析程序进行分析计算。钠冷快堆燃料元件性能分析程序FIBER从2011年开始开发,用于分析处理正常和预期瞬态条件下的钠冷快堆燃料元件的行为,程序不仅可为辐照实验的解释提供重要信息,还可为安全分析、辐照实验前的探索性分析、模型验证等提供重要信息。

FIBER程序代码由许多理论模型、经验模型以及控制计算过程的参数组成。然而,燃料行为不能仅通过这些模型的简单组合来解释,因为燃料的行为是许多现象相互耦合的结果。因此,必须考虑几种类型的模型组合来充分再现燃料行为。从这个角度来看,必须使用尽可能多的实际测量案例来进行代码验证,以确定合适的模型及参数选择。

本文首先对FIBER程序的主要模型进行介绍,然后将调研得到的俄罗斯示范快堆BN600燃料元件的实验数据与FIBER程序计算结果进行比较,并在裂变气体释放和芯块包壳间隙、辐照变形等方面进行讨论。

1 燃料元件性能分析的计算模型

1.1 燃料元件总体介绍

FIBER程序是中国原子能科学研究院开发的钠冷快堆燃料元件性能分析程序,最初版本1.0为分析中国实验快堆燃料元件(最大燃耗6at%)的行为而开发,为满足示范快堆的应用(最大燃耗10at%),对程序功能及模型进行了扩展及验证,目前程序的版本为2.0。程序整体上可分为热分析模型、力学分析模型。程序的热学分析主要包括冷却剂传热、燃料和包壳的导热、燃料-包壳间隙的传热、裂变气体释放、重结构、裂变产物迁移(MOX)等模型。力学分析主要包括弹性、塑性(包含热压)、蠕变、燃料和包壳的接触应力、芯块开裂和重定位等模型。程序包含的主要材料特性如下:1) MOX燃料(PuO2含量范围从0～30%)或UO2燃料;2) 奥氏体不锈钢(316(Ti)SS、15-15Ti)和铁素体-马氏体钢(HT-9,EP-450)。

燃料元件的计算模型在轴向上分为若干段,每个轴向段将在径向上分成一些同心环。对于热和力学分析,都是基于轴对称的基本假设。

图1为FIBER程序的分析流程图。对于每个时间步的分析流程,首先通过线功率、冷却剂温度、间隙传热系数来进行燃料与包壳温度的计算。根据温度计算结果,计算裂变气体的释放与裂变产物肿胀,计算芯块重结构和裂变产物迁移。然后进行弹性、塑性、蠕变、接触应力的力学分析。热分析与力学分析以时间步的形式进行推进。通过时间步长的控制确保程序的稳定运行。

图1 FIBER程序的分析流程图Fig.1 Analysis flow chart of FIBER code

1.2 热分析模型

在燃料元件的热分析中,一维导热模型用于燃料元件径向温度计算,温度的计算采用有限体积法,冷却剂温度是热分析的边界条件,在稳定和瞬态条件下,每个轴向节点的冷却剂温度可以用功率和冷却剂流量计算得到,芯块与包壳的温度通过导热计算得到。在这个导热模型中1个芯块一般被分成100个节点,包壳在径向上一般被分成10个节点,以确保有足够的计算精度。

1) 热导率模型

对于MOX燃料的热导率模型,使用以下模型来评价混合氧化物燃料的孔隙率和密度的影响[2]。

λ=K1dK1pK2pK3xK4rλ0

K2p=1-αpP

K3x=1

(1)

式中:λ为热导率,W/(m·K);OM为氧金属比;Bu为燃耗,MW·d/kgU;αp为气孔修正系数;P为气孔率;T为芯块温度,K。

2) 间隙传热模型

芯块与包壳之间的间隙传热模型采用了改进的Ross和Stoute模型[3-5]。该模型由3部分组成:氦气与裂变气体的气体导热;包壳和芯块表面的固体接触传热;包壳和芯块表面之间的辐射传热。模型可评估在稳态时随着燃耗而变化的间隙宽度下的间隙传热,以及在瞬态时随着接触力的变化而变化的固体接触传热。间隙传热模型如下:

(2)

式中:hgas、hcon、hr分别为气体、接触、辐射换热系数,W/(cm2·K);λgas为混合气体的热导率,W/(cm·K);δ为间隙,cm;C为粗糙度修正系数;R1、R2分别为芯块、包壳表面粗糙度,cm;g1、g2为气体跃迁距离,cm;λm为芯块与包壳等效热导率,W/(cm·K);pcon为芯块与包壳接触压力,MPa;R为等效粗糙度,cm;H为包壳的硬度,MPa;r1、r2分别为芯块与包壳尺寸,cm;ε1、ε2为辐射发射率;σ为斯蒂芬玻尔兹曼常数;T1、T2分别为芯块、包壳温度,K。

1.3 芯块重结构模型

因为快堆燃料芯块径向功率的分布是均匀的,其温度高于压水堆燃料的,在快堆燃料中,会发生由孔隙迁移和晶粒生长引起的重结构现象(中心孔和柱状晶粒形成)[6]。中心孔的模拟是通过气孔迁移模型[7]实现的,柱状晶区的形成是通过晶粒长大模型与气孔迁移实现的。

P(r,0)=P0

(3)

式中:r为半径,cm;vp为气孔迁移速率,cm/s;Δr为网格宽度,cm;Δt为时间步长,s;P0为初始气孔率。

通过质量守恒即可计算得到中心孔尺寸:

(4)

1) 气孔迁移的速率

孔隙的迁移速率考虑了温度与温度梯度的影响[8-9],具体如下:

(5)

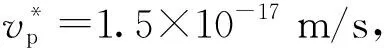
2) 晶粒长大模型

晶粒的长大模型考虑了温度与裂变气体的影响[10],有:

(6)

K=5.24×107exp(-2.67×105/RT)

(7)

1.4 裂变气体释放模型及辐照肿胀模型

1) 裂变气体释放模型

整个裂变气体释放模型的计算流程如图2所示,首先计算晶粒的生长尺寸,根据晶粒生长后的尺寸插值得到新的裂变气体分布。然后根据裂变率计算晶粒内部气泡的尺寸、气泡的密度。通过求解球形晶粒的扩散方程,计算得到扩散进入晶粒边界的裂变气体数量。根据温度与外界环境条件,计算晶粒边界气泡可储存的最大裂变气体量,裂变气体的量大于阈值时,裂变气体将被释放到气腔。

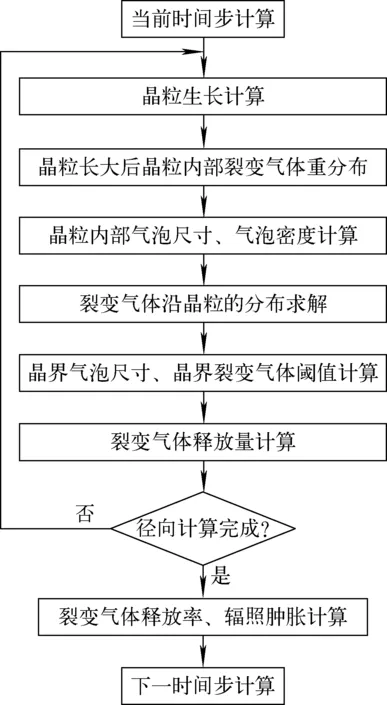
图2 裂变气体释放计算流程图Fig.2 Fission gas release flow chart

裂变气体扩散方程模型基于理想球形晶粒的方程给出[8,11],裂变产生的气体原子溶于基体中,由于浓度梯度扩散的作用向晶粒边界移动。溶于基体的气体原子与储存在晶粒内部气泡的气体原子的数量取决于捕获与再溶解的平衡。气体原子在晶粒中的扩散和被晶粒内部气泡捕获由以下方程描述:

(8)

式中:c为裂变气体晶粒基体中的原子数,cm-3;D为气体原子的扩散系数,cm2/s;g为气体原子被晶粒内部气泡捕获的速率,s-1;b′为气体重新溶于晶粒基体的速率,s-1;m为气泡内单位体积原子数,cm-3;q为单位体积芯块气体原子产生率,cm-3·s-1。

晶粒内部的气泡数量通过WHITE模型[11]进行计算,气泡的尺寸变化是通过晶内气泡的气体状态方程计算得到:

(9)

(10)

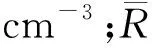
裂变气体扩散到达晶界,在晶界上形成了棱镜状的气泡[12],棱镜状的气泡所能储存的裂变气体的数量是通过气体状态方程来确定的。当晶界气泡储存的量超过阈值时,气体将形成隧道,气体立即从晶粒释放到气腔。

(11)

式中:pgas为气体压力,Pa;R为气泡半径,cm;n为裂变气体数量;f(θ)为晶粒边界气泡形状函数。

2) 辐照肿胀

裂变气体导致的辐照肿胀由晶粒内部气泡与晶界气泡两部分组成。

(12)

晶粒内部气泡体积肿胀为:

(13)

晶界气泡体积肿胀为:

(14)

式中:K为气泡的数量;Vgrain为晶粒体积,cm3;f(θ)为棱镜状气泡的形状函数,右边分母中的2表示1个气泡是由2个晶粒共享的。

3) 气腔压力

计算中假设裂变气体是理想气体,并且棒中的压力是均匀的,计算方法如下:

(15)

1.5 力学分析模型

力学分析模型中,应力/应变分析采用有限元方法,用四自由度的四边形单元进行,每个节点都有一个自由度,芯块径向的网格划分数可以是10～100。假设所有节点的轴向位移相同。使用虚功原理,时间tn+1的平衡条件[13]表示如下:

(16)

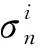
作用于燃料元件的芯块和包壳的外力如图3所示,在轴向上,包壳受到弹簧产生的轴向力,包壳外表面受到一回路冷却剂产生的压力,内表面除了受到裂变气体产生的压力,还受到芯块对包壳的接触作用力。

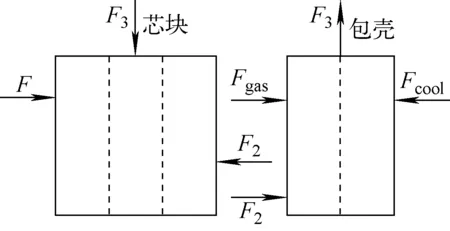
图3 作用于芯块和包壳的力Fig.3 Forces acting on fuel and cladding

力学分析计算的流程如图4所示。首先计算与应力无关的变形,例如致密化、辐照肿胀、热膨胀等,然后计算单元的弹性模量等材料属性,然后组装刚度矩阵,通过刚度矩阵计算应力-应变,应变收敛后通过迭代确保接触应力的计算是收敛的。假如出现接触到无接触,无接触到接触状态的改变的现象,应采用时间步截断的方式,在芯块-包壳间隙为0、接触应力为0的时间点截断,所有与时间相关的物理量根据时间进行插值,重新设计时间步长进行下一步的计算。

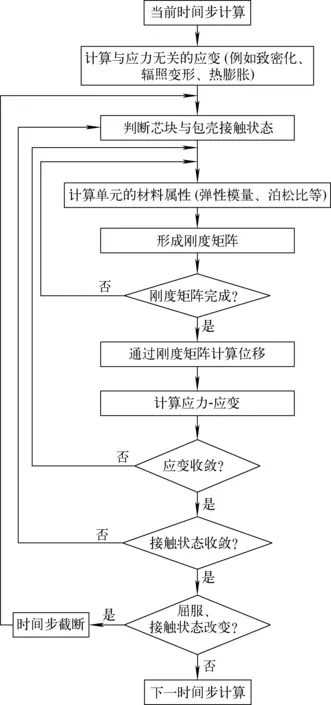
图4 力学计算流程图Fig.4 Mechanical flow chart

1.6 时间步控制

为保证程序计算过程的稳定,采用了如下的时间步控制。

1) 在1个时间步长内,线功率的变化在10 W/cm以内[4]。

2) 在1个时间步长内,燃耗的变化在0.05at%以内[4]。

3) 在裂变气体释放的模块中,时间增量Δt是由扩散方程模型求解方法决定的[4,11,13]。

Δt≤0.05(ΔR)2/D

(17)

式中:ΔR为网格的宽度,cm;D为裂变气体的扩散系数,cm2/s。

4) 在有限元弹塑性计算中,为保证蠕变计算的稳定,应使蠕变应变增量不超过弹性应变[13]。

(18)

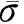
5) 为保证物质迁移的稳定性,应确保网格内物质的含量不会出现负值,即:

Δt≤nVj/(Jj,l-Jj,r)

(19)

式中:J为通过截面的物质的量,mol/s;n为单位体积物质的量,mol/cm3;V为体积,cm3。

6) 在非稳态的温度计算过程中,时间步长的限制如下[14-15]。

(20)

式中,a为热扩散系数,cm2/s。

7) 芯块-包壳接触应力计算中的时间步截断[14-15]。

对于时间步执行直到t→t+Δt的计算,芯块与包壳的接触状态从非接触到接触变化或从接触到非接触式变化时,会对时间步截断,减小时间步长Δt,确定间隙宽度变为零的时间或接触压力变为零的时间t′,所有时间相关的物理量都会随时间线性插值。然后,改变在时间t′的接触状态,并重新计算从t′到t+Δt的物理量。

2 快堆燃料元件的算例验证

为保证钠冷快堆燃料元件性能分析程序FIBER选用的模型及计算假设的合理性,应采用实验数据验证程序计算的准确性。本文调研得到了俄罗斯示范快堆BN600的UO2燃料元件和MOX燃料元件的尺寸和运行参数,具体列于表1与图5。BN600-标准燃料元件为示范快堆BN600的驱动燃料元件,该燃料元件的包壳材料为1515Ti系列奥氏体不锈钢,芯块为17%富集度的UO2,稳态运行3个周期,累计满功率559 d。该燃料元件主要进行了裂变气体释放量、气体体积、辐照肿胀等关键参数的测量[16-20]。BN600-MOX燃料元件为示范快堆BN600的试验燃料元件,该燃料元件的包壳材料为1515Ti系列奥氏体不锈钢,芯块为MOX燃料,包壳直径略小于标准燃料元件,燃料元件稳态运行3个周期,累计满功率559 d。该燃料元件主要进行了柱状晶区、包壳尺寸、间隙等关键参数的测量[16-20]。

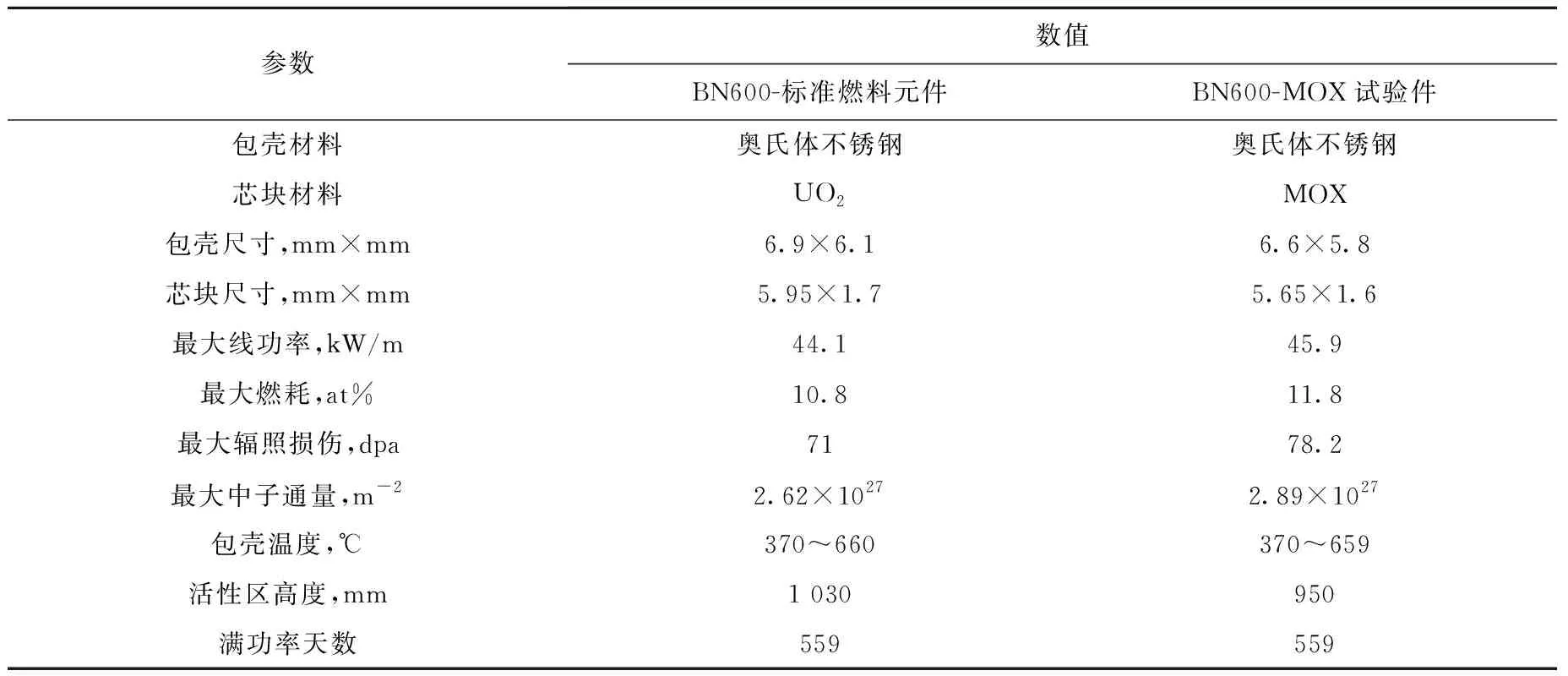
表1 BN600燃料元件参数[16-19]Table 1 BN600 fuel element parameter[16-19]

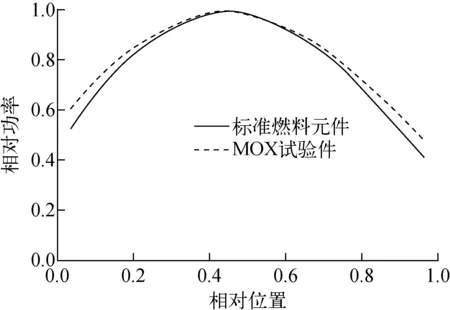
图5 相对功率分布Fig.5 Relative power distribution

采用钠冷快堆燃料元件性能分析程序FIBER对表1中的燃料元件建模计算,燃料元件沿径向分环,沿轴向分段进行计算。

2.1 裂变气体释放的验证

图6为BN600-标准燃料元件最大燃耗4at%～10at%裂变气体的测量结果[17,20],对30根燃料元件进行穿刺,得到了标准状态下的气体体积(包含初始充入氦气),图中横坐标为标准状态下的气体体积除以燃料元件中芯块的质量,纵坐标为燃料元件最大燃耗。30根燃料元件均在BN600反应堆第一流量区稳态运行,组件流量相同,运行过程中燃料组件并不移动位置,燃料元件的运行时间不同,所达到的最大燃耗不一致。从图6可看出,FIBER程序计算结果与实验结果的趋势一致,可很好地反映气腔中裂变气体的变化。

图6 裂变气体释放量计算结果与实验结果对比Fig.6 Comparison of fission gas release calculation results with experimental data

图7为7根BN600-标准燃料元件燃耗裂变气体压力的测量结果[17,20],气体的压力是在20 ℃下测量得到。从图7可看出,FIBER程序计算结果与实验结果的趋势一致,最大相对误差为26%。

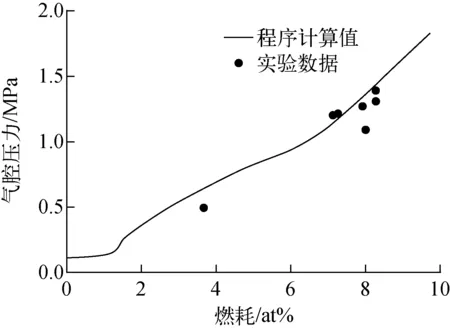
图7 气腔压力计算结果与实验结果对比Fig.7 Comparison of plenum pressure calculation results with experimental data

2.2 芯块辐照变形

文献[17,20]测量得到的UO2芯块的辐照变形,具体数据如图8所示,当燃耗超过4at%,燃料元件的肿胀随燃耗线性增加。在燃耗为9at%～10at%时,体积变形为9%～10%,在这种情况下,UO2芯块的径向辐照变形率为每1%燃耗为0.33at%。需要说明的是,原始数据为示范快堆运行的燃料元件的测量结果,未记录初始燃料芯块的尺寸,变形率按照表1的名义尺寸进行统计,燃料芯块的公差为-0.15～0 mm,因此图中出现了径向变形率小于0的情况。采用程序对上下公差芯块进行计算,从图8可看出,程序计算结果与实验结果的趋势一致。

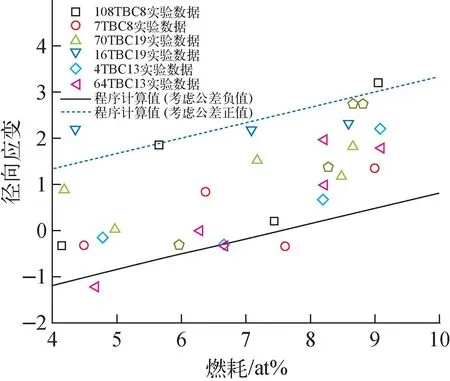
图8 UO2芯块变形计算结果与实验数据的对比Fig.8 Comparison of UO2 pellet strain results with experimental data

大部分的MOX燃料的径向变形率[17,20]与UO2芯块的径向变形率相同,即每1%燃耗为0.33at%,但部分芯块变形率达到了每1%燃耗为0.6at%～0.7at%。这部分燃料的径向变化率有一部分裂变产物迁移的贡献,在辐照后MOX燃料与包壳的间隙检测到了Mo、Cs等裂变产物形成的氧化物(简称JOG=Joint Oxyde-Gaine),如图9所示。同样需要说明的是,原始数据为示范快堆运行后燃料元件的测量结果,未记录初始燃料芯块的尺寸,变形率按照表1的名义尺寸进行统计。燃料芯块的公差为-0.15～0 mm,采用程序对上下公差芯块进行计算,并考虑JOG的贡献,从图9可看出,程序计算结果与实验结果的趋势一致。

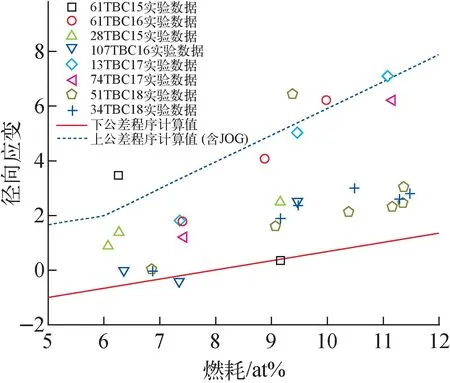
图9 MOX芯块变形计算结果与实验结果的对比Fig.9 Comparison of MOX pellet strain results with experimental data

2.3 包壳尺寸

图10为MOX试验件的测量结果[17,20],对两根燃料元件7个位置进行了测量,横坐标为相对高度(距离燃料段底端高度/燃料段总高度,下同),纵坐标为包壳管外径测量结果。包壳的尺寸从原始的6.6 mm最大增加到6.9 mm。需要说明的是,由于周围棒束及外套管的约束作用,辐照肿胀后包壳管的截面不再是圆形,截面呈现椭圆形,如图11所示,同一燃料元件位置的数据包含了椭圆形长轴与短轴的测量结果。

图10 包壳变形计算结果与实验数据的对比Fig.10 Comparison of cladding strain results with experimental data

图11 辐照前后包壳形状Fig.11 Shape of cladding before and after irradiation

从图10可看出,程序计算结果与实验结果的趋势一致。实验数据与程序计算结果差异较大的点出现在相对位置0.19处,在实验中该位置观察到了芯块较大的变形(每1%燃耗为0.7at%)。该位置包壳的变形可能是芯块较大的变形引起的接触应力导致的。程序计算结果与实验数据的偏差可能是程序只考虑了径向的物质迁移,未考虑轴向裂变产物迁移,芯块变形率计算偏小导致的,同时程序假设JOG并不会对芯块与包壳的接触有贡献,只对传热有贡献。

根据辐照数据及程序结算结果推测,活性区中平面附近芯块的外表面温度1 050 ℃,间隙温度755 ℃,高温下JOG为液态。但随着时间推移,活性中平面的JOG沿轴向迁移至燃料元件的底端,该位置的温度相对较低,芯块的外表面温度622 ℃,间隙温度521 ℃,JOG在燃料元件的底端凝固。铯会与燃料发生化学反应[21],引入铯与燃料的化学反应肿胀,该物质会对芯块与包壳的接触应力有很大的贡献。目前程序对JOG的模型不够完善,后续考虑基于辐照现象对该部分模型进行修改。

2.4 间隙尺寸对比

图12为MOX试验件的测量结果[17,20]。由于芯块开裂以及包壳辐照变形后形状的不规则,同一位置包含多个测量结果。从图12可看出,程序计算结果与实验结果的趋势一致。相对位置0.93处出现较大的偏差,可能是由于该位置的芯块初始芯块尺寸偏小。

图12 间隙计算结果与实验结果对比Fig.12 Comparison of gap calculation results with experimental data

2.5 柱状晶区尺寸

图13为MOX试验件的柱状晶粒范围的测量结果[17,20]。从图13可看出,程序计算结果与实验结果的趋势一致。

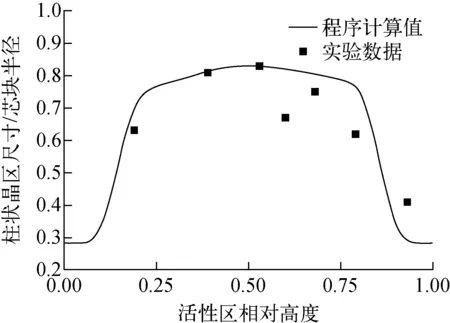
图13 柱状晶粒范围的计算结果与实验结果对比Fig.13 Comparison of columnar region calculation results with experimental data

3 结论

本文对钠冷快堆燃料元件性能分析程序FIBER的热分析、芯块重结构、裂变气体释放、力学、时间步控制模型进行了介绍,并通过调研获取了俄罗斯BN600反应堆两种类型燃料元件的辐照后检验结果,通过实验数据验证了FIBER的计算结果。结果表明,程序可模拟最高燃耗11.8at%、辐照损伤78 dpa燃料元件辐照变形、柱状晶区、裂变气体释放的现象。