基于自动重要抽样方法的减方差技巧体系构建与验证

武 祯,郝以昇,浦彦恒,周 扬,杲申申,邱 睿,*,马锐垚,张 辉,李君利

(1.清华大学 工程物理系,北京 100084;2.粒子技术与辐射成像教育部重点实验室,北京 100084;3.同方威视技术股份有限公司,北京 100084)

辐射屏蔽系统的设计与分析对核设施的安全具有重要意义,随着核电技术的发展,对精细化屏蔽计算的要求越来越高。使用蒙特卡罗方法进行屏蔽计算可准确地模拟粒子的行为,与其他方法相比,其在计算精度、物理模型的完备性、几何描述能力等方面具有无可比拟的优势[1]。但蒙特卡罗方法也存在收敛速度慢、计算较费时的缺点,这成为其在实际工程中应用的主要障碍。Wagner等[1]按照计算目标将粒子输运问题分为源-探测器问题、区域问题和全局问题,为解决这3类问题中存在的深穿透问题,研究人员提出了一系列减方差技巧。按照实现原理,目前已有的减方差技巧可分为偏倚、半解析和耦合减方差方法[2]。几何重要性方法和权窗方法是使用广泛的偏倚减方差方法,它们通过人为修改粒子权重和数量减小方差。半解析减方差方法包括隐式俘获法、统计估计法、点通量法和DXTRAN球法等,它们主要通过在粒子输运中运用解析方法降低方差,然而其并没有改变粒子的随机游动过程,因此对于深穿透问题效率提升不大。耦合减方差方法的特点是进行多次计算,其中一类是在空间上进行耦合,例如确定论和蒙特卡罗的空间耦合[3-4],其利用确定论方法计算大屏蔽、几何简单部分,而利用蒙特卡罗方法计算源项、几何复杂的部分;又例如蒙特卡罗空间分层面源续算方法[5-8]也属于空间耦合方法。另一类是利用一次计算给出合理的几何重要性或权窗参数,再利用几何重要性或权窗方法进行二次计算。根据一次计算的方法可分为蒙特卡罗正算、蒙特卡罗伴随、确定论正算和确定论伴随。一次计算采用正算的耦合减方差方法适用于全局问题和部分区域问题,利用正算通量与权重的正比关系生成权窗参数。文献[8]用确定论程序进行一次计算正算生成空间上的权窗参数,文献[9]将其扩展为空间-能量网格。采用蒙特卡罗程序进行一次计算正算的方法有MAGIC方法[10]和基于蒙特卡罗正算的全局减方差方法[11]等。一次计算采用确定论伴随计算的一致性共轭驱动重要抽样(CADIS)[12]方法最初适用于源-探测器问题,改进后的前向加权一致性伴随驱动重要抽样(FW-CADIS)[1]方法适用于区域问题和全局问题。一次计算采用蒙特卡罗伴随计算的耦合减方差方法方面,邱有恒等[13]曾仿照CADIS方法在MCNP上使用多群伴随蒙特卡罗计算生成源偏倚和权窗参数。

为了解决深穿透问题[14-15],清华大学辐射防护与环境保护实验室提出了自动重要抽样(AIS)方法的减方差技巧[16-19],且在为辐射屏蔽计算设计开发的中子/光子/电子耦合输运蒙特卡罗程序MCShield[20]中进行了实现。AIS方法引入基于重要性采样和统计估计方法的虚拟面,将空间划分为多个子空间层,虚粒子在虚拟面上产生并传送到下一个子空间,随后,进行自动粒子权重调整和数量控制,使虚拟面上的虚粒子数与源粒子数相等。AIS方法需要在源项与统计区域之间定义一系列虚拟面。在MCShield程序中,用户可根据实际需求,沿特定方向设置平面、圆柱面和球面3种类型的虚拟面,同时需要保证虚拟面在计算区域内不相交。虽然AIS方法在解决区域问题时取得了良好的效果[2],但在源-探测器问题和全局问题应用时效率还不是很高,因此MCShield研究团队后续又基于AIS方法提出了一系列减方差技巧用于解决这两类问题。本文以此为基础构建基于AIS方法的减方差技巧体系,并对其中的部分减方差技巧进行验证。

1 基于AIS方法的减方差技巧体系

屏蔽计算问题根据计算目标不同可分为源-探测器问题、区域问题和全局问题。针对不同的目标,适用的减方差方法不同,MCShield研究团队针对这3类问题提出了基于AIS方法的系列减方差技巧。源-探测器问题通常分为小体积探测器问题和迷宫孔道两类问题,针对小体积探测器问题,提出了小探测器自动重要抽样(SDAIS)方法和AIS伴随蒙特卡罗的耦合减方差(AIS-CADIS)方法。SDAIS方法基于探测器位置进行虚粒子数量控制并将AIS方法与指向概率结合,AIS-CADIS方法将AIS方法引入伴随蒙特卡罗输运计算中,利用AIS伴随生成源偏倚和权窗参数减小探测器的统计误差[20-21]。针对迷宫孔道问题,提出了FPAIS方法[2,22],采用方向概率引导粒子输运,以实现减方差的目的。

在区域问题中,往往需要处理大体积和多个探测器。针对区域问题,提出了CNP-AIS方法[2],采用统计估计法和分层输运法实现中子-光子耦合输运。针对全局问题,涉及较大的空间尺度,提出了网格化-AIS方法[20],使整个空间的粒子密度尽可能均匀,以获得统一的全局统计误差。以上述系列减方差技巧为基础,本文构建了基于AIS方法的减方差技巧体系,如图1所示。

2 源-探测器问题减方差技巧验证

2.1 小探测器自动重要抽样方法验证

MCShield研究团队采用NUREG/CR-6115 PWR压力容器计算基准题[23]对SDAIS方法进行验证,选取该基准题的标准核燃料组件布局方案,计算反应堆堆腔内中子剂量仪的中子通量。反应堆中子剂量计位于反应堆腔体内径向距离r=319.56～320.56 cm和轴向高度z=176.27～178.27 cm处,如图2所示。

图2 NUREG/CR-6115 PWR基准题几何示意图Fig.2 NUREG/CR-6115 PWR benchmark geometry diagram

分别采用MCShield程序的几何重要性法(IMP-MC)、AIS方法和SDAIS方法进行计算,比较3种方法的正确性和效率。其中,AIS方法使用4个圆柱形中子虚拟面,半径分别为188、215、230和300 cm。SDAIS方法与AIS方法相比,除了使用半径分别为188、215、230 cm的3个圆柱中子虚拟面外,还进行两点改进:1) 考虑虚粒子位置对探测器贡献的影响,添加修正因子1/d2(d为虚粒子距离探测器的距离)对虚粒子的数量进行控制,达到将更多的粒子向探测器区域输运的目的;2) 在探测器所在位置处设置一个DXTRAN球,中心坐标为(317.04 cm,43.85 cm,177.27 cm),外球半径为7 cm,内球半径为6.5 cm,增加粒子到达探测器区域附近并在其中发生碰撞的概率。

本算例中,选取基准题中确定论程序DORT作为基准参考结果,使用品质因子(FOM)来评估计算效率,FOM定义为:

FOM=1/(R2T)

(1)

其中:R为统计误差;T为计算时间。

堆腔中子剂量仪通量(E>0.1 MeV)列于表1,其中,归一化通量表示由每个粒子引起的通量。可看出,中子通量在中子剂量仪中的衰减约为10-10cm-2。上述方法的计算结果与DORT程序结果基本一致,SDAIS方法的计算效率约为IMP-MC的56倍、AIS方法的7倍。事实证明,SDAIS方法对于源-探测器的问题具有更高的计算效率。除对反应堆堆腔的中子剂量仪的中子通量进行验证外,还验证了混凝土屏蔽层内的中子通量[22]。

表1 堆腔中子剂量仪通量Table 1 Reactor cavity neutron dosimeter flux

2.2 AIS伴随蒙特卡罗方法验证

基于伴随计算的耦合减方差方法在源-探测器问题中具有良好的效果。目前基于伴随计算的耦合减方差方法中,主流的方法是在一次计算中使用确定性伴随计算的CADIS方法。基于蒙特卡罗方法虽也可进行伴随计算,但在深穿透问题中基于蒙特卡罗方法正向计算的伴随问题仍是深穿透问题。为解决这一问题,本文提出了一种基于AIS伴随蒙特卡罗方法的耦合减方差方法,将AIS方法引入伴随蒙特卡罗方法中,以解决深穿透问题中收敛速度慢的问题。

本文将基于AIS伴随蒙特卡罗的耦合减方差方法应用到某商用反应堆屏蔽算例的计算中。某商用反应堆屏蔽算例的二维模型如图3所示,二维切面图的切面均经过测点。探测器位于主管道的保温层内部,共有4个测点,编号为P1、P2、P3、P4,统计各测点快中子(E>1 MeV)和热中子(E<0.6 eV)通量。使用MCNP原始伴随程序和AIS伴随程序分别生成源偏倚和权窗参数,CADIS方法中确定论方法计算的源偏倚和权窗参数作为参考。在AIS伴随方法中采取一系列球面作为虚拟面,如以P1点作为源项的伴随计算时,AIS虚拟面设置为以坐标(0 cm,-40 cm,30 cm)为球心的一系列球面,半径依次为380、320、260、200、140、100、40 cm。

图3 某商用反应堆屏蔽算例的二维模型Fig.3 Two-dimensional model of commercial reactor shielding example

以测量值为基准,统计了3种方法的计算结果与测量值的相对偏差,如图4所示。其中,AIS-CADIS代表基于AIS伴随蒙特卡罗计算的正算结果,MC-CADIS代表基于原始伴随蒙特卡罗计算的正算结果,CADIS代表使用CADIS方法的JMCT程序[24]计算结果。可看出,CADIS和AIS-CADIS在快中子通量结果上较为接近,最大相对偏差小于5%,与测量值的相对偏差也均在20%以内;在热中子通量结果上,CADIS和AIS-CADIS最大相对偏差约为20%;MC-CADIS结果较CADIS和AIS-CADIS的结果偏小超过20%,远大于相对统计误差,原因是伴随通量误差较大,导致计算偏倚源项时出现系统误差。这说明基于原始伴随蒙特卡罗的减方差方法在深穿透问题中有一定的局限性。

图4 快中子(a)和热中子(b)通量与测量值相对偏差Fig.4 Relative deviation of fast neutron (a) and thermal neutron (b) fluxes from measured value

图5为快中子和热中子通量FOM的比较。可看出,对于快中子通量结果,CADIS的计算效率约为AIS-CADIS的1～3倍。对于热中子通量结果,AIS-CADIS的计算效率约为CADIS的5～32倍。总体上说,AIS-CADIS的计算效率略优于CADIS。

图5 快中子(a)和热中子(b)通量FOM比较Fig.5 Comparison of fast neutron (a) and thermal neutron (b) flux FOM

3 全局问题减方差技巧验证

本文通过简化的反应堆屏蔽计算算例验证了网格化-AIS方法,图6为自设反应堆屏蔽算例几何示意图。

图6 简化反应堆屏蔽算例几何示意图Fig.6 Geometry diagram of simplified reactor shielding calculation example

反应堆堆芯是一半径为0.5 m、高为1 m的圆柱体,其下表面与水层底部共面。防护罩外侧为半径为1.5 m、高为4 m的水层,外侧为真空边界的1 m混凝土层。两根0.1 m半径的空气管分别在径向和轴向穿过水层和混凝土层。中子源各向同性,能量分布符合瓦特裂变谱。本算例测试了直接蒙特卡罗方法、AIS方法和网格化-AIS方法在各向异性较强几何下的计算表现,3种方法计算得到的中子通量及相对统计误差三维分布沿空气管道中心处的切面如图7～9所示。表2列出了简化反应堆屏蔽算例计算结果。网格化-AIS方法的平均相对统计误差为3.3%,在实际屏蔽计算中,通常要求相对统计误差需要小于5%。另外,网格化-AIS方法的FOM是AIS方法的12倍左右,是直接蒙特卡罗方法的290倍左右。

表2 简化反应堆屏蔽算例计算结果Table 2 Calculation result of simplified reactor shielding example

图7 直接蒙特卡罗方法的通量(a)及相对统计误差(b)Fig.7 Analog Monte Carlo method flux (a) and relative statistical error (b)

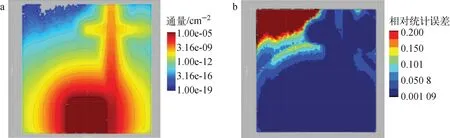
图8 AIS方法的通量(a)及相对统计误差(b)Fig.8 AIS method flux (a) and relative statistical error (b)

图9 网格化-AIS方法的通量(a)及相对统计误差(b)Fig.9 Grid-AIS method flux (a) and relative statistical error (b)

4 区域问题减方差技巧改进

对于区域问题使用的减方差方法CNP-AIS,需要在源项与统计区域之间定义一系列的平面、圆柱面或球面虚拟面,将整个计算区域划分为多个子空间。在实际应用中,虚拟面需要用户凭借经验进行设置,计算结果的准确性和效率取决于虚拟面设置的好坏。在不同的几何条件下,虚拟面的设置方法及最优位置的选择是不同的,这也就要求用户具备较为丰富的屏蔽计算经验,不利于程序的通用性。同时,目前AIS方法仅支持平面、圆柱面或球面3种虚拟面,不足以适应各种复杂几何的情况。

为解决以上问题,本文结合CADIS方法,提出了适用于复杂几何的虚拟面自动生成与调整算法,其基本过程为:1) 读取各CADIS方法计算的相空间网格参数,得到计算空间中各网格的响应贡献分布情况;2) 基于网格的响应贡献分布生成源偏倚参数,同时绘制响应贡献分布等值面,基于等值面自动生成多个网格虚拟面,用于后续的AIS方法虚粒子生成;3) 将虚拟面所在网格中的能量权重结果进行汇总,生成该虚拟面的能量权重参数,用于对虚拟面上的虚粒子进行能量权重修正;4) 在对到达虚拟面的虚粒子进行再抽样时,需要将该虚粒子自身的权重乘以其对应能量权重参数,再对其进行轮盘赌或分裂生成新的虚粒子,然后作为下一个子空间的源粒子进行继续输运。

5 结论

本文对MCShield研究团队针对屏蔽计算深穿透问题研发的基于AIS方法的系列减方差技巧进行了总结,构建了基于AIS方法的减方差技巧体系,用于解决区域问题、源-探测器问题和全局问题,并对其中的一些方法进行了介绍及验证。采用NUREG/CR-6115 PWR压力容器计算基准题验证了SDAIS方法,结果表明SDAIS方法对于源-探测器问题的计算效率高于AIS方法。提出了AIS-CADIS方法,将AIS方法引入到蒙特卡罗伴随计算中,对某商用反应堆主管道内的测点通量进行了计算验证,结果表明,该方法与CADIS方法的效率相当,且仅使用一套程序,避免了确定论与蒙特卡罗耦合计算带来的问题。针对全局问题,使用简化的反应堆屏蔽计算算例验证了网格化-AIS方法,结果表明,与AIS方法和直接蒙特卡罗方法相比,网格化-AIS方法可有效提升计算效率。