基于cosRMC的同位素电池屏蔽计算研究
王益祺,刘仕倡,*,靳程建,李 锐,孙宁延,韩 毅,张 显,陈义学
(1.华北电力大学 核科学与工程学院,北京 102206;2.中国辐射防护研究院,山西 太原 030006;3.辐射安全与防护山西省重点实验室,山西 太原 030006)
热电式同位素电池系统作为一种新型能源系统,在深空、深海探测任务中有广泛应用。相比于常规能源,热电式同位素电池具有比功率高、寿命长、适应外部环境能力强、运行稳定的优势[1-2]。钛酸锶热源是一种纯β衰变放射源,广泛应用于热电式同位素电池中。钛酸锶热源中的放射性同位素90Sr和90Y会发射β射线,β射线与物质作用产生韧致辐射,韧致辐射具有很强的穿透力,需要为同位素放射源安装屏蔽层,以降低辐射剂量。为评估其中的同位素衰变产生的放射性对外界的影响,需要对同位素电池进行高精度屏蔽计算。
蒙特卡罗方法具有复杂几何描述准确、计算精度较高等优点,因此广泛应用于同位素电池的屏蔽计算。伊朗沙赫鲁德理工大学的Zohreh等[3]在选择放射源时,考虑到所需放射性同位素的半衰期与期望从同位素电池获得的寿命之间的匹配,选择90Sr+90Y作为同位素电池的放射源,为了确定合适的电极,使用蒙特卡罗程序MCNP的计数卡得到电极吸收和击中的β粒子数,从而计算电极的效率。韩国原子能研究所的Souza等[4]在63Ni放射源外放置屏蔽层以防止放射性物质泄漏,为评估保护层厚度对电子吸收的影响,使用蒙特卡罗程序MCNP6对放射源的辐射强度进行计算,得到不同厚度保护层下表面粒子数的变化。日本船舶研究所Ohashi等[5]利用蒙特卡罗程序MCNP4A研究了通过添加分级结构来降低90Sr放射性同位素电池热源模型辐射剂量的可能性,结果显示,3层、4层和5层基础结构的剂量分别减少了17%、19%和22%。中国原子能科学研究院的刘诗蕾等[6]在90Sr放射源中加入少量石墨材料,使用蒙特卡罗程序MCNP对90Sr放射源的韧致辐射强度进行了计算,结果表明,在热源中加入少量石墨材料,有效降低了放射源产生的韧致辐射;马俊平等[7]采用蒙特卡罗程序MCNP对放射性同位素电池进行屏蔽计算,得到剂量率随屏蔽层厚度的变化。当屏蔽层厚度超过一定值后,蒙特卡罗方法计算结果的统计误差显著增大[8]。通过大量增加蒙特卡罗程序追踪的粒子数,可以减小统计误差,但将耗费大量时间。减方差技术通过引导更多粒子输运到目标区域,增加统计样本,从而减小统计误差,提高计算效率,在MCNP、cosRMC等蒙特卡罗程序中有广泛应用。通过减方差技术可以有效降低屏蔽层外部区域的蒙特卡罗统计误差,从而提高热电式同位素电池屏蔽计算的准确性。同时,由于电子输运模拟耗时很长,而厚靶韧致辐射(TTB)模型可以近似处理由光子产生的二次电子,假设光子诱导的电子被立即转化为轫致辐射光子,与电子输运相比可以显著提高计算速度,因此可以通过TTB模型处理电子产生的光子,从而提高计算效率[9]。
cosRMC是由国家核电软件开发中心和清华大学联合研发的自主化蒙特卡罗粒子输运程序,cosRMC中开发了栅元重要性减方差技术和中子-光子-电子耦合输运模拟功能[10]。cosRMC针对反应堆计算的需求进行开发,具有屏蔽计算、燃耗计算、临界计算等计算分析功能,可用于反应堆堆芯设计分析和辐射屏蔽计算,尚未在同位素电池屏蔽计算中应用。本文拟开展cosRMC程序的减方差技术和TTB模型在同位素电池屏蔽计算中的应用研究及验证。参考美国SNAP-21结构对热电式同位素电池进行精细建模和屏蔽计算,并与MCNP结果进行比较,从而分析cosRMC 程序在热电式同位素电池屏蔽计算中的准确性,并在此基础上对栅元重要性减方差方法的效果进行分析。
1 cosRMC计算方法
1.1 光子-电子耦合输运
在光子-电子的耦合输运中,光子可以通过光电效应、康普顿效应和电子对效应产生电子并存储于临时电子库中,产生的电子在模拟光子历史后被提取并输运。电子可以通过韧致辐射和正电子-电子湮灭产生光子并存储于临时光子库,产生的光子在模拟电子历史后被提取并输运。光子-电子的耦合输运的相互作用示于图1。

图1 光子-电子耦合输运的相互作用Fig.1 Interaction of photon-electron coupled transport
与光子输运相比,电子输运需要大量的时间。为了减少计算时间,常用TTB模型近似电子产生的二次光子,该模型仅考虑厚靶韧致辐射中产生的光子的能量分布,韧致辐射光子的位置和运动方向由位置和运动近似。与电子输运相比,TTB模型可以大幅减少计算时间[11]。
1.2 栅元重要性减方差
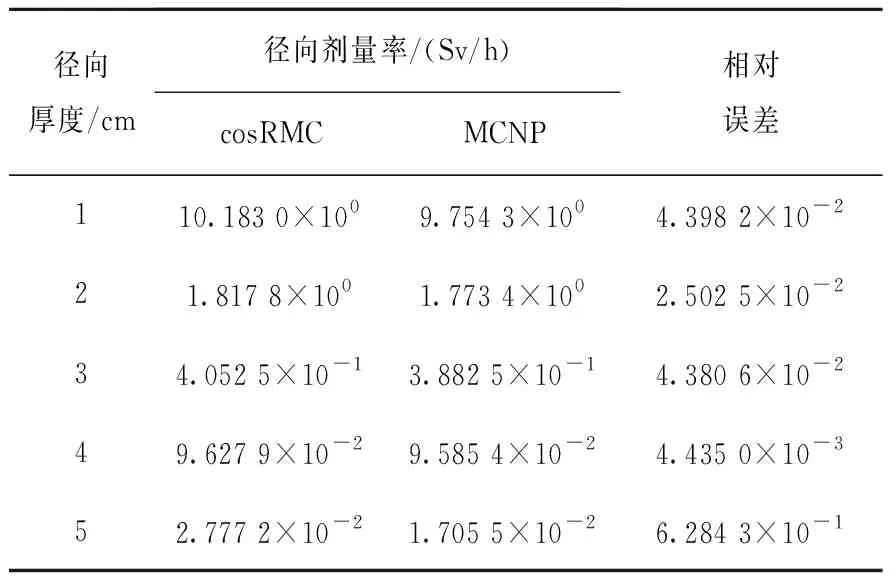
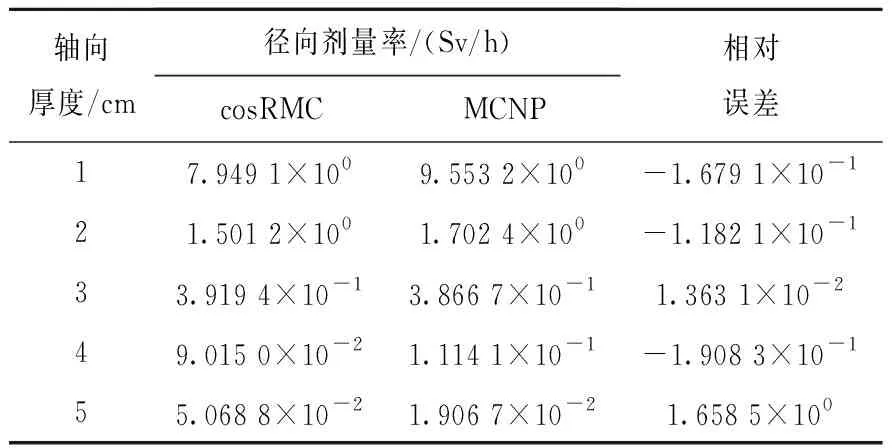
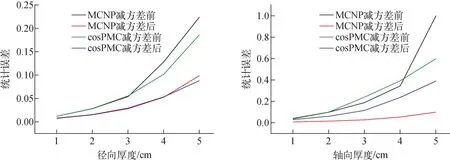
栅元重要性是常用的减方差技巧,该方法主要对计算模型的不同区域定义不同的重要性数值,当粒子从重要性低的区域飞入重要性高的区域时,由于分裂机制会产生更多的粒子;反之,当粒子从重要性高的区域飞入重要性低的区域时,会进行轮盘赌[12]。当粒子向非计算所需区域输运时,程序会终结粒子的历史。粒子的几何分裂与轮盘赌如图2所示。由图2可见,当粒子从重要性为IA的栅元A输运到重要性为IB的栅元B时,如果IB>IA,当前粒子将会进行分裂,分裂为n个粒子,n为IB与IA之比,为了结果的无偏性,每个粒子的权重变为之前的1/n;反之,若IB 图2 几何分裂与轮盘赌示意图Fig.2 Diagram of geometric split and roulette 在编写MCNP和cosRMC程序的输入卡时,使用IMP指定栅元的重要性[13]。但栅元重要性在相邻栅元之间相差不能太大,否则会增加程序的抽样负担。因此,设置相邻栅元的重要性比值不大于4,数值设置按照2的指数变化[14]。 在屏蔽计算中,随着粒子穿透深度和屏蔽层厚度的增加,穿透屏蔽层的粒子数减小,统计误差增大。为减小程序的统计误差,本文对电池热源及热源外部的结构依次设置了不同的栅元重要性,以达到减小统计误差的作用。 SNAP-21是美国3M公司研发的深海放射性同位素燃料热电式发电机供电系统[15],其结构如图3所示。参照SNAP-21结构和典型同位素电池的设计方案[16],对热电式同位素电池的结构进行建模,如图4所示。 图3 SNAP-21 10 W热电式同位素电池Fig.3 SNAP-21 10 W thermoelectric isotope battery 图4 热电式同位素电池总体结构Fig.4 Overall design of thermoelectric isotope battery 钛酸锶热源中的放射性同位素90Sr在衰变过程中会发射β射线,其最大能量为0.546 MeV,衰变产物为90Y,90Y会进行β衰变,β射线最大能量为2.28 MeV,产物为稳定的90Zr。90Sr和90Y衰变过程中都会发射β射线,β射线在穿过钛酸锶热源时与其原子核会发生相互作用,产生轫致辐射[6]。 同位素电池共有4块热源,2块热源组成1个热源盒,热源结构由2个热源盒连接组成。 在热源结构外是热屏蔽层,虽然热源盒采用不锈钢外壳,但表面辐射仍很强。热屏蔽有内屏蔽和外屏蔽。高容量电池通常采用内屏蔽;小型电池因制造方便和隔热材料安装方便,采用外屏蔽。在内屏蔽中,90Sr衰变产生的2.28 MeV的β射线射程只有2 mm,不锈钢屏蔽层厚度不低于2 mm即可阻挡轫致辐射。 本文设计的屏蔽结构如图5所示,包括内屏蔽和外屏蔽结构,内屏蔽用于屏蔽β射线,外屏蔽用于屏蔽轫致辐射时放出的X射线。 图5 屏蔽结构示意图Fig.5 Schematic diagram of shielding structure 使用cosRMC程序计算90Sr同位素电池屏蔽层外表面的剂量率,计算过程如下。 1) 对同位素电池结构进行精确的几何描述。结合同位素电池结构建立径向和轴向计算模型,如图6所示。 图6 90Sr同位素电池的径向和轴向计算模型Fig.6 Radial and axial calculation models of 90Sr isotope battery 2) 依据钛酸锶热源的几何构造和参数以及材料特点和参数,设计本文使用的通用源的数据卡。 3) 通过面计数卡,记录屏蔽层贫铀外表面的通量分布。为获得平均剂量率,通过Dose选项卡将面通量转化为剂量。 计算中电子为源粒子,钛酸锶热源中电子的取向是等向性的,钛酸锶热源的衰变能量遵循其自身的β射线能量概率分布。钛酸锶热源发射的β射线能量所对应的概率如表1所列。 表1 钛酸锶热源发射的β射线能量所对应的概率Table 1 Probability of β ray energy emitted by SrTiO3 heat source cosRMC模拟的是1个放射源,其结果需乘以粒子的放射性强度,本文采用的热源粒子的放射性强度为6.29×1014Bq[6-7]。 本文在分别在贫铀屏蔽层的径向和轴向的不同厚度上进行通量统计,追踪的粒子数为1×108个。两程序关于贫铀径向和轴向剂量率的相对误差列于表2、3。 表2 贫铀径向剂量率两程序计算结果对比Table 2 Comparison of calculation results of two programs for radial dose rates of depleted uranium 表3 贫铀轴向剂量率两程序计算结果对比Table 3 Comparison of calculation results of two programs for axial dose rates of depleted uranium 从表2、3可看出,随着屏蔽层厚度的增加,剂量率呈指数下降,MCNP与cosRMC所得径向及轴向剂量率的相对误差均随贫铀屏蔽层厚度的增加而增大。相对误差的合理性与对应厚度处的组合统计误差σ有关,σ的计算公式如下: (1) 贫铀径向和轴向剂量率的相对误差和组合统计误差示于图7。从图7可以看出,随着贫铀厚度的增加,相对误差均落在±3σ范围内,说明两程序符合良好。 图7 贫铀径向和轴向剂量率相对误差和组合统计误差Fig.7 Depleted uranium radial and axial dose rate relative deviation and combined statistical error 随着电池径向和轴向贫铀厚度的增加,两程序的统计误差逐渐增大,因此使用栅元重要性对电池径向和轴向进行减方差计算,减方差前后两程序所得的统计误差如图8所示。 图8 减方差前后两程序的统计误差Fig.8 Statistical error of two programs before and after variance reduction 由图8可看出,减方差后两程序的统计误差均有大幅减小。由于电池径向5 cm处和轴向4 cm处统计误差很大,对结果有较大影响,所以对径向5 cm处和轴向4 cm处减方差计算前后的相对误差和组合统计误差σ进行误差分析,结果列于表4、5。 表4 电池径向5 cm处两程序计算结果减方差前后对比Table 4 Before and after comparison of minus variance at 5 cm radial of depleted uranium 表5 电池轴向4 cm处两程序计算结果减方差前后对比Table 5 Before and after comparison of minus variance at 4 cm axial direction of depleted uranium 从表4、5可看出,在电池径向5 cm处和电池轴向4 cm处,减方差后两程序的相对误差均明显减小,且相对误差均落在±3σ范围内,进一步说明两程序在同位素电池的屏蔽计算上符合良好。 本文基于美国SNAP-21结构的设计方案,采用cosRMC程序对同位素电池进行了精细建模,通过改变径向和轴向外屏蔽层贫铀的厚度分析其对表面剂量率的影响,同时通过厚靶韧致辐射模型处理电子产生的光子,并与MCNP结果进行比较。结果表明,在径向和轴向使用不同厚度的屏蔽层,cosRMC与MCNP计算的贫铀屏蔽层表面剂量率的相对误差在±3σ区间内符合良好。经栅元重要性减方差后,两程序统计误差均减小,在径向5 cm处和轴向4 cm处,cosRMC的统计误差分别减小了52.515%和39.338%,且cosRMC与MCNP所计算的剂量率相对误差在±3σ区间内符合良好,进一步验证了cosRMC程序进行热电式同位素电池屏蔽计算的准确性。同时,采用栅元重要性减方差方法可以有效提高同位素电池屏蔽计算的准确性。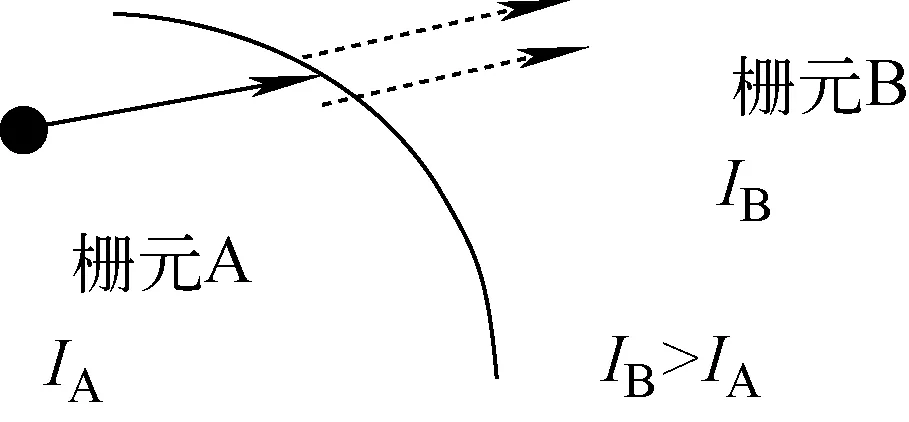
2 热电式同位素电池建模


2.1 热源结构
2.2 屏蔽结构
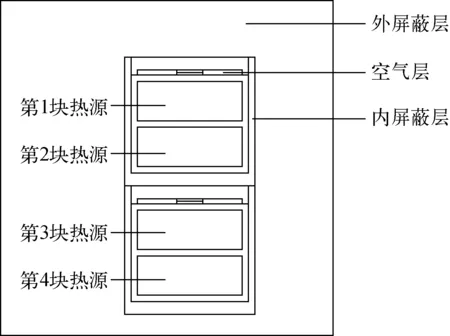
3 屏蔽计算及结果分析
3.1 屏蔽计算
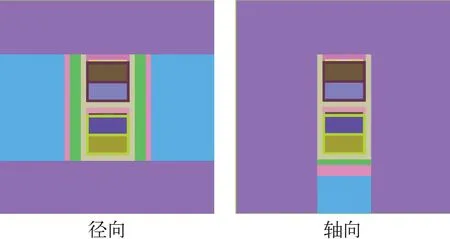
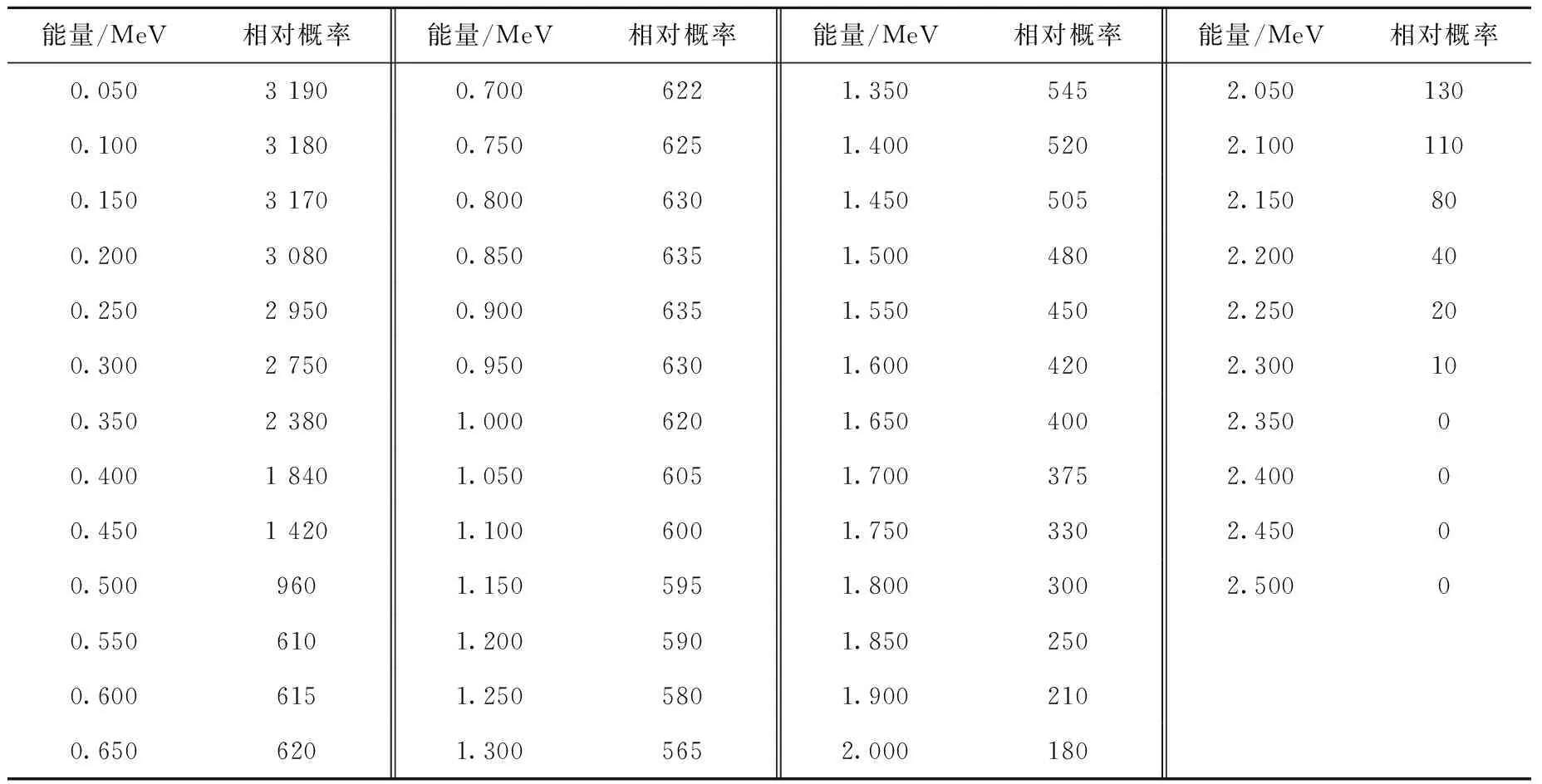
3.2 结果分析



4 结论

