液态金属冷却快堆子通道分析软件SACOS-LMR研发与工程应用

王金顺,陈荣华,朱昕阳,田家豪,田文喜,秋穗正,苏光辉

(西安交通大学 核科学与技术学院,陕西 西安 710049)

我国已确立了压水堆-快堆-聚变堆三步走的核能发展战略,快堆在这一战略路线中发挥着承上启下的关键作用,以钠冷、铅铋或铅冷为代表的液态金属冷却快堆则是其中最主流的堆型。在核反应堆设计中,堆芯的热工水力特性分析是反应堆安全的前提,为提高堆芯的安全性能,要求尽可能精确地计算出堆芯的热工参数。子通道分析方法目前是反应堆堆芯详细热工水力分析的一种相对精确的计算方法。考虑到液态金属快堆堆芯的结构特点,有必要在压水堆子通道分析程序的基础上进行改进。韩国原子能研究所基于COBRA-Ⅳ-Ⅰ和MATRA程序,开发了适用于钠冷快堆带绕丝燃料组件的稳态及瞬态分析子通道程序MATRA-LMR,并利用所开发程序对HYPER堆芯燃料棒束进行了热工水力分析[1-2]。上海交通大学[3]在COBRA的基础上开发了COBRA-LM,可用于液态金属反应堆堆芯子通道计算分析,程序采用ORNL19棒束实验进行了验证。中国科学技术大学[4]自主开发了铅基堆子通道分析程序KMC-Sub,程序通过ORNL19棒束实验和KYLIN台架的61棒束实验完成了验证。博洛尼亚大学Lodi等[5]开发了适用于液态金属快堆热工安全分析的子通道程序ANTEO+,可用于堆芯组件的稳态计算分析。

西安交通大学热工水力研究室在液态金属快堆热工水力特性分析方面开展了大量研究,积累了大量的研究经验和软件开发基础[6-12],本文基于自主开发的子通道程序SACOS[13],通过添加液态金属快堆特有的模型,如绕丝模型、盒间流模型、液态金属对流换热模型等,采用SIMPLE算法和交错网格技术完成子通道计算模型的求解,形成适用于液态金属快堆的子通道热工安全分析程序SACOS-LMR;为了验证程序的功能和计算精度,对德国卡尔斯鲁厄核研究中心开展的37棒束钠冷瞬态实验[14]的稳态工况和沸腾前瞬态工况进行对比计算;基于验证后的SACOS-LMR子通道程序对欧洲铅冷快堆(ALFRED)[15]开展稳态工况和瞬态事故工况下的热工安全特性分析,以证明SACOS-LMR子通道程序在液态金属快堆的堆芯设计和热工水力计算方面的能力。

1 数值方法

1.1 控制方程

在液态金属冷却快堆堆芯内不大可能发生沸腾现象,因此本研究的模型中没有考虑铅铋的沸腾导致的两相流动和换热。对于单相液态金属,其可压缩性很小,可看成是不可压缩流体,忽略其中的重力、压力以及动能变化所做的功,并忽略轴向导热,假设流体无内热源,并且假设相邻子通道之间的湍流交混不产生质量交换,则可得到以下热工水力分析模型,依次为质量守恒方程、能量守恒方程、轴向动量方程和横向动量方程。

(1)

(2)

(3)

(4)

式中:A为流通面积,m2;ρ为冷却剂密度,kg/m3;t为时间,s;m为轴向质量流量,kg/s;z为轴向高度,m;wij为横向质量流速,kg/(m·s);h为焓值,J/kg;w′ij为湍流质量流速,kg/(m·s);h*为i与j通道间隙处焓值,J/kg;GD为热导因子;λ为热导率,W/(m·K);s为间隙宽度,m;l为湍流长度,m;T为通道流体温度,K;Qrad_con为相邻通道流体径向导热,W;u为轴向速度,m/s;p为压力,Pa;g为重力加速度;α为流动方向与竖直方向夹角,rad;f为摩擦阻力系数;De为子通道i的水力当量直径,m;Ks为局部形阻系数;Kg为横向流动阻力系数;下标i和j为通道编号,N为通道i相邻的子通道总数。图1为子通道划分示意图。

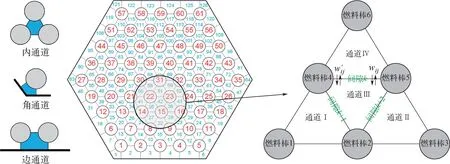
图1 子通道划分示意图Fig.1 Schematic diagram of sub-channel division

1.2 燃料棒导热模型

SACOS-LMR程序可对燃料棒或加热棒进行建模,并可考虑棒在径向、周向的导热:

(5)

式中:cp为比定压热容;λ为热导率;r为半径;φ为周向方向上的角度,考虑到周向控制体数量只能和相邻子通道个数保持一致,因此无法按照周向角度精细划分,燃料棒内部导热计算节点划分如图2所示;qV为单位体积热源。燃料棒包壳表面温度T采用第三类边界条件计算:

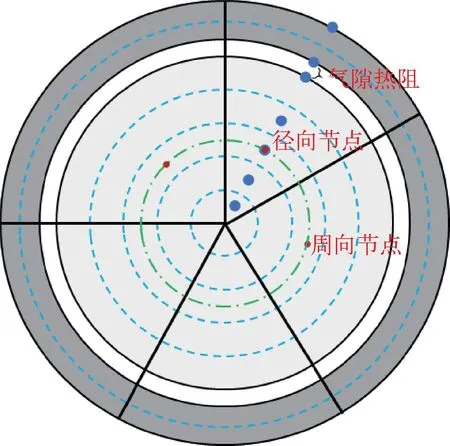
图2 燃料棒导热控制体划分Fig.2 Heat conduction node in fuel rod

(6)

其中:ht为燃料棒壁面换热系数,W/(m2·K);下标w和f分别为冷却剂和壁面。

1.3 辅助模型

1) 绕丝模型

为了封闭上述横向动量方程(式(3)),需要对沿程摩擦阻力系数fi和局部形阻系数Ksi进行计算。液态金属快堆组件常采用绕丝定位棒束,如图3所示。绕丝的存在将大大影响冷却剂的流量和温度分布,一方面,棒束总压降增大,另一方面,绕丝改变了流体在包壳表面的流动方向,增大了通道间的横流交混。因此,绕丝模型在子通道分析中十分重要。Novendstern[16]结合以前所有的实验方法和实验数据,提出了适用于六边形绕丝棒束的摩擦阻力系数计算模型。本研究采用Novendstern模型或UCTD模型[17]来计算fi,而由于局部形阻系数Ksi过于依赖经验,常通过用户根据局部形阻特征给定,在此不予考虑。在Novendstern模型中,通过有效摩擦系数feffect来表征绕丝带来的影响,在光管阻力系数fsmooth上乘以倍增系数M得到带绕丝燃料棒的有效阻力系数,摩擦阻力系数fi由下式确定:

图3 绕丝定位的六边形组件Fig.3 Hexagonal assembly with helical wire-wrap spacer

(7)

(8)

式中:L为燃料元件的长度,m;Vi为通道i的冷却剂流速,m/s;M为倍增系数,主要由节径比(P/D)、栅径比(H/D)以及雷诺数确定。

(9)

Novendstern模型适用范围为:棒数19～217,P/D范围1.06～1.42,H/D范围8.0～96.0,且适用于过渡区和紊流区,雷诺数范围2 600～105。

UCTD模型是Chen等[17]在CTD模型的基础上改进得到的,优化了层流雷诺数的预测精度并修正了组件压降随棒数变化趋势异常的问题。相比于Novendstern模型,UCTD模型在层流湍流及过渡流做了更细致的区分和计算,相对更加精确。

(10)

(11)

式中,CfiL和CfiT为湍流常数,与燃料棒和绕丝的几何参数有关。

2) 换热系数模型

国内外关于液态金属冷却的棒束通道内的流动换热系数模型研究得较多,其中 Mikityuk模型[18]的适用范围更广,平均偏差低于5%,且开发年代较近,模型如下:

Nu=0.047(1-e-3.8(P/D-1))(Pe0.77+250)

(12)

式中,Pe为佩克莱数,表示对流与扩散之比。Mikityuk模型适用范围为1.1

此外,程序中还内置了Kazami和Carelli开发的Westinghouse换热关系式[19],即:

(13)

3) 湍流交混模型

相邻子通道间冷却剂在流动过程中存在着横向质量、动量和能量的交换,这种横向的交换统称为交混。由于交混的存在,各通道内的冷却剂流量沿轴向将不断发生变化,热通道内冷却剂的温度和焓会有所降低。因此,准确模拟冷却剂交混是子通道分析的关键之一。交混主要分为湍流交混、横向流动、流动散射和流动扫掠4种形式。横向流动是由于子通道间的横向压差导致的定向流动,通过式(4)右边第一项横向压差作用力项考虑。流动散射和流动扫掠分别是由定位件引起的非定向交混和定向横流,现有研究还不能够精细描述机理规律,因此在SACOS-LMR软件中将定位件的影响叠加在湍流交混效应中考虑。湍流交混本质上是子通道间流体脉动时自然涡团扩散引起的非定向交混。方程(2)～(4)中的湍流交混项w′ij为:

(14)

β=0.007 479Re-0.1

(15)

4) 液态金属对流换热模型

本文开发的液态金属子通道分析程序适用于液态钠、铅铋和铅作为冷却剂的快堆。世界经济合作组织核能署(OECD/NEA)在2015年出版的铅铋手册中对前人的一些实验结果进行了整理和分析,总结出一套液态铅铋合金的物性模型[21],如表1所列。Fink等[22]在1995年发布的钠物性报告中,推荐了液态钠的热物性,如表2所列。

表1 液态铅铋和铅的物性(397.9～2 021 K)[21]Table 1 Property of liquid LBE/Pb (397.9-2 021 K)[21]

表2 液态钠的物性[22]Table 2 Property of liquid sodium[22]

1.4 求解策略

相对于传统子通道软件(如COBRA-EN)采取的牛顿辛普森算法,采用自下而上的方式对整个流体域进行逐层求解并对出口流量进行修正,在求解中低流量时收敛性较好,在求解倒流、回流和极低流量时收敛效果不佳,而SACOS-LMR采用的SIMPLE算法,对整个轴向流体域建立全局矩阵,同时迭代求解,能够对局部倒流不收敛的情况进行优化,具体求解流程如图4所示。

图4 SACOS-LMR程序求解流程Fig.4 Solution process of SACOS-LMR code

2 程序验证

2.1 37棒束钠冷瞬态实验[14]

37棒束钠冷瞬态实验是在德国卡尔斯鲁厄核研究中心的KNS钠回路上进行的37棒束失流实验。图5为KNS 37棒实验段及功率分布。参考SNR-300堆芯组件,棒的排列方式为六边形组件中的三角形排布,采用电加热棒进行加热,热功率分布类似于正弦分布,并由下式计算:

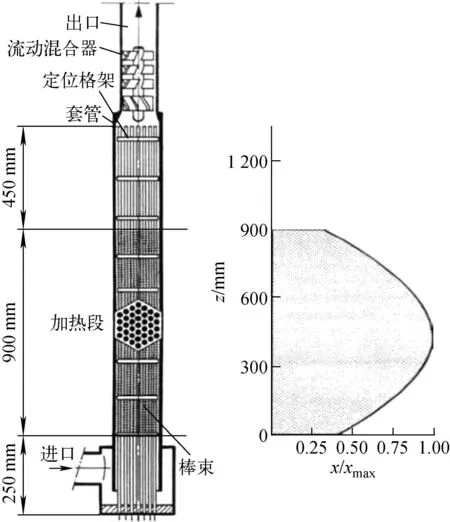
图5 KNS 37棒实验段及功率分布[14]Fig.5 KNS 37-pin experiment section and power distribution[14]

(16)

其中:x为单根棒的线功率,W/cm;z为加热段底部位置的距离,mm;xmax为单根棒的最大线功率,W/cm。

实验段由200 mm的零功率入口段和900 mm的加热段以及450 mm的零功率出口段组成。KNS 37棒束的其他几何参数列于表3。

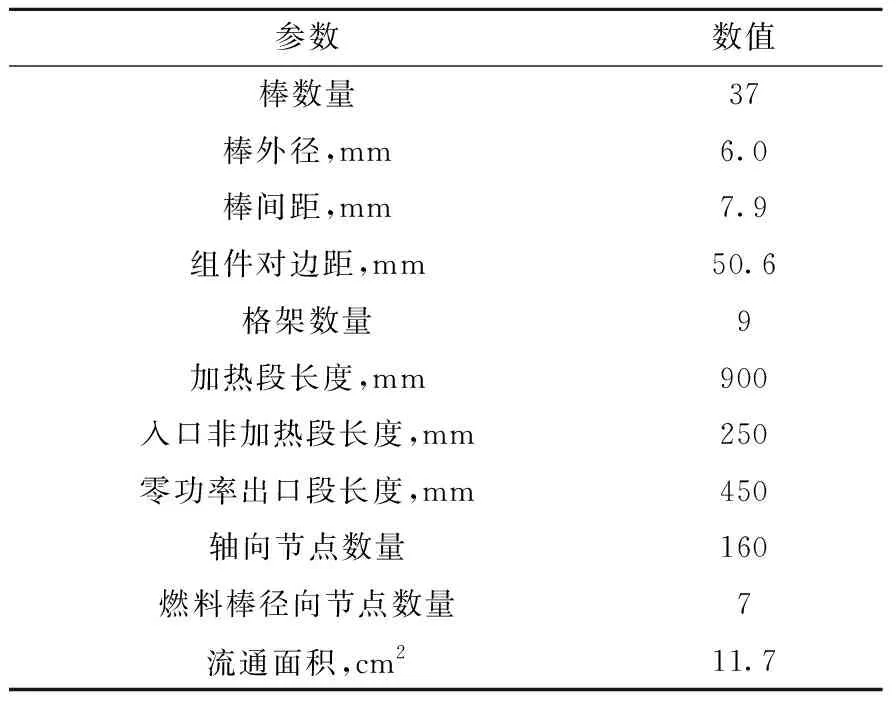
表3 KNS 37棒实验段几何参数Table 3 Geometric parameters of KNS 37

KNS 37棒钠冷实验共进行了3种形式的失流实验(L22、L26和L29),实验中通过控制泵转速和阀门来控制实验段的入口流量。本文选取L22实验进行程序验证,分为两个工况,其具体参数列于表4。对于沸腾前工况的计算,考虑到SACOS-LMR程序目前还未扩展至汽液两相,因此随着入口流量不断减小至钠沸腾前即停止计算。

表4 KNS 37棒实验边界条件Table 4 Boundary conditions of KNS 37

2.2 计算结果

基于上述实验参数建立KNS 37棒L22实验稳态工况和沸腾前工况的SACOS-LMR计算模型,计算中考虑到实验段向周围环境的热损失,推荐使用6.7 W/(m2·K)的换热系数以及40 ℃的环境温度来计算实验段的热损失。

图6为稳态工况和钠沸腾前工况中心子通道钠温度的轴向变化。可看到,稳态工况和沸腾前工况下程序计算所得中心钠温度与实验值趋势符合较好,稳态工况最大偏差在20 ℃以内(为进出口温升的12.2%),沸腾前工况最大偏差在25 ℃以内(为进出口温升的6.8%)。两种工况下,在零功率出口段附近的冷却剂温度偏差较大,且相较于实验值都普遍预测偏低。由于金属堆温度普遍较高,若采用传统方法计算温度误差,则误差数值过小难以反映计算的准确性,因此采用相对偏差(RD)表示,如式(17)所示:

图6 稳态工况和沸腾前工况中心通道钠温度轴向变化Fig.6 Variation of axial sodium temperature in central channel of steady case and before boiling

(17)

图7为稳态工况下压力沿轴向的变化,可看到程序具备计算格架定位件阻力系数的功能,计算的进出口压降与实验值符合较好。图8为沸腾前工况距离加热段底部779 mm高度处径向(90°～270°方向)的温度分布。可看到,最大偏差在45 ℃以内(为进出口温升的12.2%),边通道的偏差最大。对于实验中90°和270°方向的对称子通道内的温度出现不对称倾斜的情况,可认为是实验段制造工差引起的。

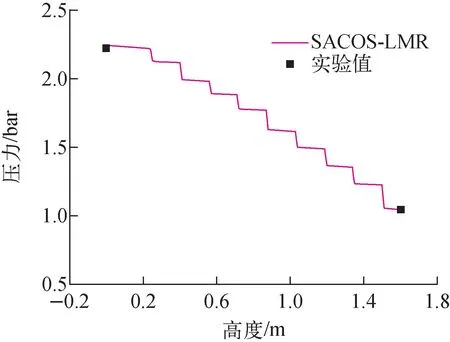
图7 稳态工况压力轴向变化Fig.7 Variation of axial pressure of steady case

图8 沸腾前工况下1 029 mm截面上子通道温度分布Fig.8 Temperature distribution at 1 029 mm before boiling

SACOS-LMR对KNS 37棒实验稳态和瞬态过程的计算结果可表明,程序具备稳态和瞬态的计算功能,且温度场的相对偏差在15%以内,程序对进出口压降的预测精度较高,能够捕捉流量等瞬态过程的变化。

3 程序应用

ALFRED(Advanced Lead Fast Reactor European Demonstrator)是一个欧洲的核反应堆项目。ALFRED反应堆目前处于设计和开发阶段,预计未来几年开始建设。ALFRED反应堆的堆芯由171个燃料组件(FA)组成,根据流量和功率分为4组,如图9所示,而燃料组件的几何和物理参数列于表5。

表5 燃料组件的几何和物理参数Table 5 Geometrical and thermal-hydraulic parameters of ALFRED FA

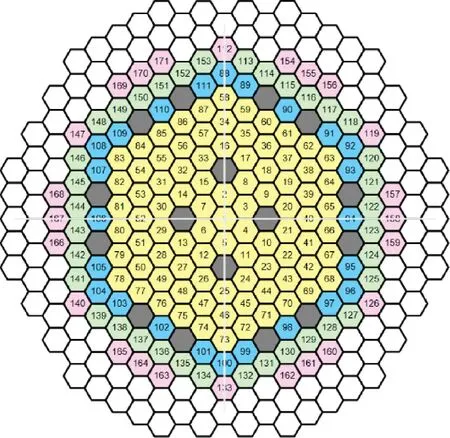
图9 ALFRED燃料组件分组[23]Fig.9 Fuel assemble groups in core of ALFRED[23]

基于上述验证可认为SACOS-LMR具备对液态金属快堆堆芯进行稳态和瞬态计算与分析的能力。因此采用SACOS-LMR程序对ALFRED堆芯进行热工水力计算,用于评估其热工水力特性。

图10为中央燃料组件活性区出口截面的温度云图。可看到,内通道的温度最高且分布相对均匀,约为490 ℃。边缘通道的温度最低,约为473 ℃,而6个角通道的温度较高,接近483 ℃。最热的燃料棒为中心燃料棒,这与Petrovich等[23]的计算结果一致。在高度方向上,最热燃料棒的燃料包壳外表面、包壳内表面、燃料芯块表面、燃料芯块中心以及铅冷却剂的温度变化示于图11。可看到,燃料芯块的最高温度出现在0.335 m位置,为1 832.3 ℃,低于2 000 ℃的设计限值。包壳的最高温度出现在出口处,为544.4 ℃,低于550 ℃的设计限值。

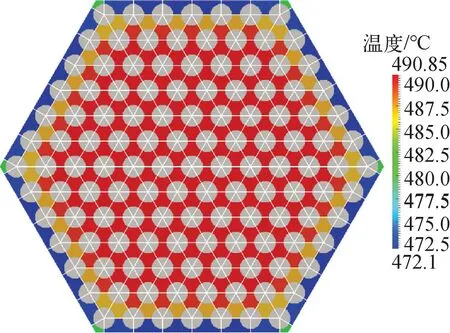
图10 冷却剂温度及最热棒表面温度分布Fig.10 Coolant temperature and circumferential temperature of hottest rod

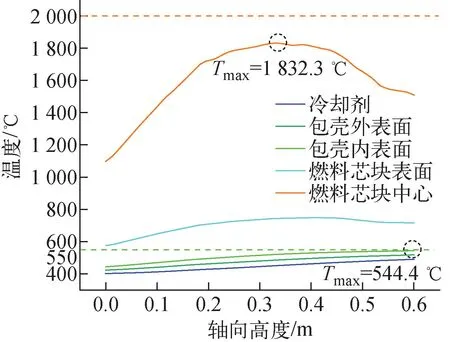
图11 中心棒轴向温度变化Fig.11 Axial variation of temperatures in central fuel rod

表6为Petrovich[23]采用ANTEO-LFR子通道软件与SACOS-LMR软件计算的最高温度的对比,二者相对偏差在15%以内。图12为中心燃料棒在0.335 m处的内部温度云图。可看到,气隙热阻造成了约210 ℃的温差,芯块表面至芯块中心温差达到1 000 ℃。

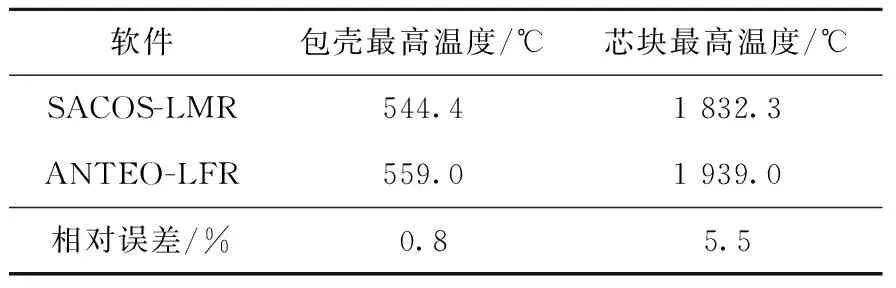
表6 中心组件燃料棒最高温度对比Table 6 Comparison of maximum temperature of central FA

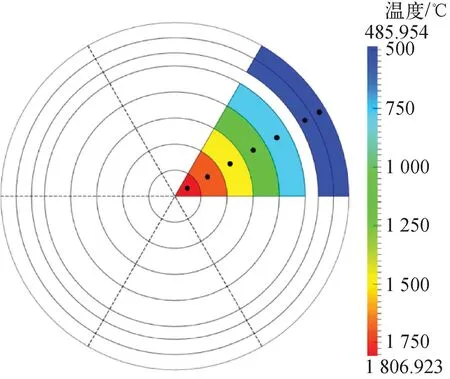
图12 中心燃料棒内部温度分布Fig.12 Temperature distribution inside central fuel rod

图13为中央燃料组件的质量流量和流速分布。可看到,角通道的流量相对较低,导致局部温度较高。尽管包壳温度低于设定的限值,但仍存在一定的安全隐患。可考虑调整几何参数,即P/W和P/D,从而优化流量分布,在堆芯中实现更均匀的温度分布。

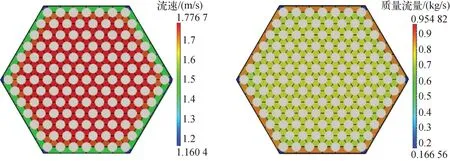
图13 出口截面流速和质量流量云图Fig.13 Distributions of velocity and mass flow rate

为了进一步探究P/W对温度场和流场的影响,在保证组件对边距和边界条件不变的情况下,开展了P/W的敏感性分析。图14展示了提取参数的子通道编号。图15为不同P/W下出口处温度、质量流量和流速的径向分布。可发现,P/W的变化对内通道影响不大,对边通道影响较大,对角通道影响最大。随着P/W的增大,内通道温度减小,边通道和角通道温度增大,流量和流速则呈相反的变化趋势。此外可发现,当P/W为2.070时,温度、流量和流速的径向分布更加平均,对堆芯热工安全更加有利。图16为不同P/W下最高温度的变化。可发现,随着P/W的增大,芯块最高温度下降了6.9 ℃,包壳最高温度下降了7.8 ℃,冷却剂最高温度上升了7.9 ℃,而此时节径比P/D仅从1.3增加到1.325,足以说明P/W和P/D对堆芯内局部热点的分布有重要影响。

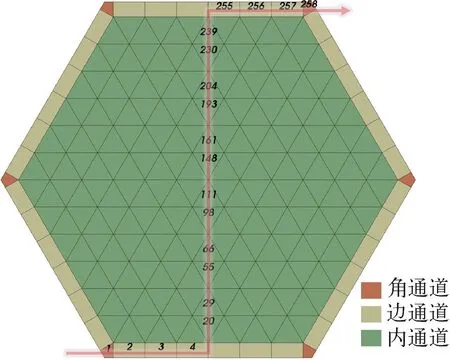
图14 子通道编号Fig.14 Measured sub-channel number

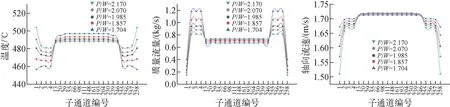
图15 P/W对热工水力参数的敏感性分析Fig.15 Sensitivity analysis of P/W to thermal-hydraulic parameters

图16 P/W对燃料棒和冷却剂最高温度的敏感性分析Fig.16 Sensitivity analysis of P/W on maximum temperature of fuel rods and coolants

此外,为了分析SACOS-LMR程序的瞬态运行特性,对ALFRED进行了假设的事故场景计算分析,即无保护流失(ULOF)事故。ULOF瞬态是由所有主泵停机引起的。因此,系统逐渐进入一种主冷却剂质量流量不断下降的连续过程,直到自然循环模式接管。自然循环堆芯质量流量为39.9 kg/s(额定值的21%)。

图17为ULOF事故发生后中心燃料组件入口质量流量和出口温度的变化。芯块峰值温度(PFT)在25 s内从1 832 ℃迅速降低至1 395 ℃,300 s内略有上升直至稳定在1 405 ℃,包壳峰值温度(PCT)和冷却剂出口最大温度(PCoT)在25 s内迅速上升至780 ℃和758 ℃,在50 s内降低至652 ℃和638 ℃,然后逐渐稳定不变,该计算结果与ENEA-Relap5计算结果符合良好,但芯块峰值温度始终偏低。图18为ULOF事故后中央燃料组件内最高温度的变化。

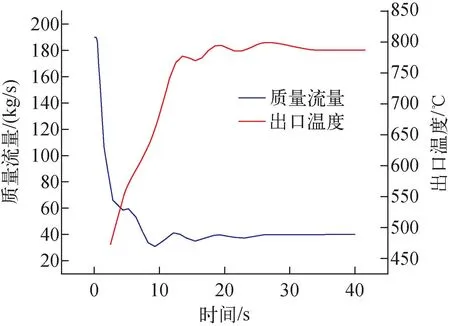
图17 中心燃料组件入口质量流量和出口温度的变化Fig.17 Variations of inlet mass flowrate and outlet temperature in central FA

图18 中心燃料组件的峰值温度变化Fig.18 Variations of peak temperature in central FA

4 结论

本文基于西安交通大学热工水力研究室自主开发的适用于压水堆的子通道程序,通过添加液态金属快堆特有的模型,如绕丝模型、盒间流模型、液态金属对流换热模型等,开发了适用于液态金属快堆的子通道分析程序SACOS-LMR;同时结合卡尔斯鲁厄核研究中心开展的37棒钠冷瞬态实验,完成了SACOS-LMR程序的瞬态功能验证。程序计算的温度场的相对偏差在15%以内,温度最大偏差为25 ℃;采用SACOS-LMR程序对ALFRED堆芯开展了热工安全特性分析,稳态计算结果与ANTEO-LFR的相对偏差在5%左右,预测的包壳最高温度为544.4 ℃,芯块最高温度为1 832.3 ℃,均满足设计限值要求;发生假想ULOF事故后,包壳峰值温度在20 s时达到最大,为780 ℃,远超包壳温度的设计限值,存在安全隐患,程序计算结果与ENEA-Relap5计算结果整体上符合良好,但芯块峰值温度始终偏低。以上计算结果表明,SACOS-LMR子通道程序可用于液态金属快堆的堆芯设计和热工水力分析研究,能为中国液态金属快堆设计和工程应用提供分析工具。