LOCA事故下碳化硅复合包壳失效概率计算

曹力文 易柏全 郝祖龙

（华北电力大学 核科学与工程学院 北京 102206）

福岛事故后，耐事故燃料（Accident Tolerant Fuel，ATF）成为核燃料行业的研发重点［1-2］。作为ATF包壳候选材料之一，碳化硅（SiC）及其复合材料在堆内的热-力耦合行为与断裂失效机理受到关注，现有研究主要集中在正常运行工况下SiC包壳的应力分析与失效概率计算［3-5］。但从安全角度出发，研究失水事故（Loss of Coolant Accident，LOCA）下的SiC包壳瞬态失效行为更具有意义。

LOCA 事故发生后，随着应急冷却水的快速注入，燃料包壳表面温度开始迅速下降发生骤冷，从而对燃料包壳形成较大热冲击。相较于锆合金包壳，SiC包壳在热冲击作用下更易引发断裂失效。文献［6-7］分别利用实验和模拟计算方法研究了单质SiC 和SiC 复合包壳在LOCA 事故下的抗热冲击行为，讨论了材料热导率、尺寸结构、热冲击温度以及端塞等因素对热冲击行为的影响，但未涉及失效概率计算。Rho 等［8］在前期开发的多层SiC 包壳力学模型基础上，结合热工水力计算程序分析了LOCA下双层SiC 包壳的瞬态失效行为，计算时先模拟事故下包壳温度和内外压强，再将计算结果作为输入条件计算包壳应力和失效概率。

Rho等的研究需要分两步模拟事故下的失效概率，采用的是间接耦合方法，而本文采用了直接耦合方法。以双层SiC 复合材料包壳为研究对象，基于原有的稳态失效概率计算程序，结合LOCA 事故下包壳表面温度和内外部压力的变化趋势，计算事故瞬态SiC 复合包壳在不同时刻的失效概率，并分析不同层厚比和不同威布尔参数对SiC复合材料包壳失效概率的影响。直接耦合的优势在于，不但考虑了材料物性对温度分布的影响，同样考虑了温度对材料物性的反作用，反复迭代，直到达到稳定状态。

1 LOCA下SiC包壳失效概率计算原理

本文采用准稳态计算方法，该方法将LOCA 事故进程分解为若干个长短不一的时间步，时间步的长短由包壳壁面温度，包壳内外压强变化的剧烈程度决定。在每一个时间步长内，认为包壳处于近似稳态的状态，采取稳态计算方法计算此时包壳的应力分布，最终得到LOCA事故进程中，包壳应力场随事故后时间的变化，并据此计算碳化硅包壳在LOCA事故下的失效概率。

该方法的优点在于：在每个时间步内，进行稳态计算，将边界条件变化较大的时间步进一步细分，避免由于边界条件的剧变导致计算无法收敛。

图1 给出了LOCA 事故瞬态工况下SiC 复合材料包壳失效概率的计算方法。

图1 瞬态下碳化硅包壳失效概率的计算方法框图Fig.1 Block diagram of the failure probability calculation of SiC claddings under transient accidents

2 模型与参数

与传统锆合金相比，SiC 包壳具有极低的高温氧化速率，但由于SiC材料热导率相对较低、且具有一定陶瓷脆性，使得它在事故下的失效模式主要表现为脆性断裂失效。考虑到当前SiC包壳管的设计方式和制备工艺，本文重点考虑断裂失效风险计算问题。SiC包壳管断裂失效主要受到三个力学因素的影响，分别是内外压差、热应力和辐照应力。由于辐照应力为长期效应，LOCA事故为瞬态事故，辐照对包壳断裂失效的影响本文暂未考虑。

图2为SiC复合包壳的示意图，包壳内层为陶瓷基复合材料（Ceramic Matrix Composite，CMC），外层为SiC 单质。包壳内径r1=4.18 mm，包壳外径r3=4.75 mm，通过改变r2即可改变内外层的厚度比，研究不同CMC层厚度，对SiC复合包壳的失效概率的影响。

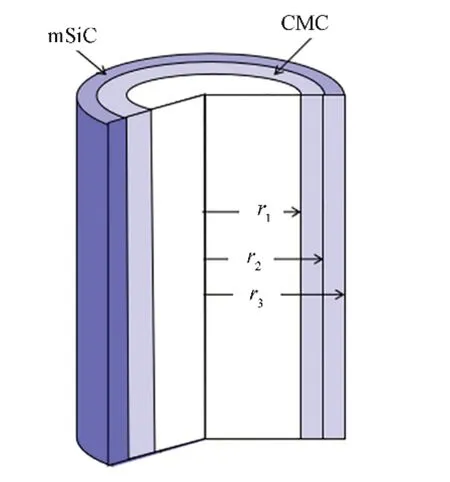
图2 双层SiC复合包壳示意图Fig.2 Schematic of a double-layer SiC composite cladding

基于文献［3］的数据，表1给出了CMC和SiC单质的材料物性参数。稳态下SiC复合包壳失效概率的计算模型，笔者在前期工作中已经给出了较为详细的阐述［9］，如式（1）～（3）所示。其中，式（1）为SiC复合材料包壳失效概率计算模型，式（2）为SiC单质失效概率计算模型，式（3）为CMC 材料失效概率计算模型。

表1 SiC包壳材料物性参数Table 1 Physical property parameters of SiC cladding materials

式中：r、θ、z分别表示包壳径向、环向和轴向；H（σ）为引入的阶跃函数；σP为比例极限应力；σU-P为比例极限应力（Proportional Limit Stress，PLS）与极限拉伸应力（Ultimate Tensile Stress，UTS）的应力差值；εU-P为PLS 与UTS 的应变差值；Pf(εU-P，σU-P，σP)为给定参数的失效概率；pdf(εU-P)、pdf(σU-P)、pdf(σP)分别为参数σP、σU-P、εU-P的概率密度函数。

由于CMC 材料具有“假塑性”（pseudo-plastic）断裂特性，其失效概率计算较为复杂。通过对PLS和UTS 的分析，可以构造出σP、σU-P、εU-P3 个应力-应变性质，将这3 个性质的概率密度函数进行积分可得到CMC材料的失效概率，具体求解过程如图3所示。

图3 CMC材料失效概率求解过程流程图Fig.3 Flowchart of process of solving the CMC failure probability

根据文献［5］可得σP、σU-P、εU-P的概率密度函数相关参数，如表2所示。

表2 相关性质分布类型及参数Table 2 Distribution types and parameters of related properties

通常CMC材料失效概率服从威布尔分布，将表2中根据文献［3，5］得到的参数代入威布尔模型后，可得σP、σU-P、εU-P的概率密度函数：

为简化计算，先分别求出3 个参数概率密度函数最大值所对应的参数值，然后取应力-应变曲线中点的杨氏模量作为CMC材料的等效杨氏模量，最后运用计算SiC单质存活概率公式近似计算出碳化硅复合材料存活概率。

3 计算结果与分析

本文模拟的LOCA 事故从第5 s 开始，第8 s 时包壳温度达到最大值，第23 s开始进入再灌水阶段。图4给出了第5 s后燃料包壳外表面温度、包壳内外压力随时间变化情况。然后以双层碳化硅包壳为对象，计算了LOCA事故下碳化硅包壳的失效概率，结果见图5。

图4 LOCA事故后燃料包壳参数变化 (a) 包壳外表面温度，(b) 包壳外压，(c) 包壳内压Fig.4 Changes in the fuel cladding parameters after a LOCA(a) Cladding surface temperature, (b) Cladding external pressure, (c) Cladding internal pressure

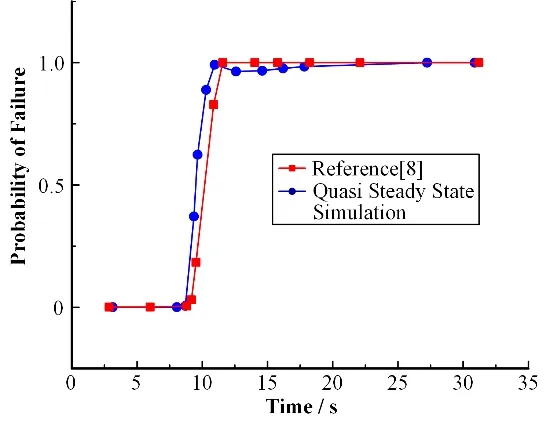
图5 LOCA事故下双层碳化硅包壳失效概率（层厚比5:5）Fig.5 Failure probability of SiC claddings under a LOCA(layer thickness ratio of 5:5)

由图4可知，在LOCA事故后，包壳表面温度和内外壁面压强变化趋势与文献［8］的模拟结果基本一致，但本文采用的方法是将包壳温度及内外表面压强与冷却水的热物性耦合，在每一个时间步内得到包壳和冷却水同时达到稳态的计算结果，再进行下一个时间步的计算，当时间步划分足够小时，便可以得到LOCA 事故后的瞬态计算结果，这样得到的结果更接近真实情况。

由图5可知，由于包壳表面温度突然上升，内外压力突然下降，包壳失效概率呈现快速上升的趋势，并在温度达到峰值时失效概率增至0.99，包壳失效概率变化趋势与文献［8］的模拟结果基本一致。但在本文的模拟中，温度达到峰值时，包壳内外压差较大，平衡了一部分热应力，因此失效概率并未达到1。之后，随着包壳表面温度下降，碳化硅包壳失效概率略有下降，但随着后来内外压差继续变大，失效概率又逐渐回升。

下面分析双层碳化硅包壳在瞬态工况下的失效概率主导因素。如图6所示，在事故发生后，由于温度突然升高，而包壳内外压差迅速降低，导致了热应力在环向和轴向的占比均逐渐升高，而机械应力占比逐渐降低。而当包壳表面温度下降后，热应力下降，因此热应力在整个应力的占比中由上升转为下降。同时，由于包壳内外压差从减小至增大，因此机械应力所占比例也由一开始的减小变为增大。因此，发生事故后包壳热应力占比较大，对包壳失效概率起到了主导的作用，在包壳表面温度下降后，虽然热应力占比也在降低，但整体上依旧高于机械应力。

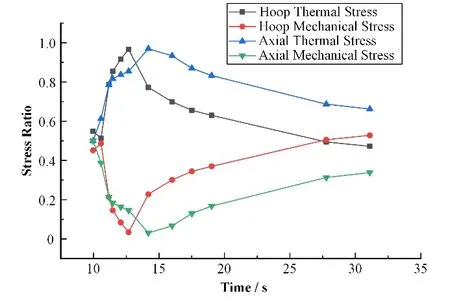
图6 环向和径向的机械应力和热应力占总应力比值瞬态变化Fig.6 Transient variation in the ratio of mechanical and thermal stresses to the total stress in annular and radial directions

1）层厚比对失效概率的影响

同时研究了不同厚度比对碳化硅复合包壳瞬态失效概率评估的影响，结果如图7所示。可知，事故后的相同时间内，当包壳外表面温度还没达到峰值前，随着处在内层的复合材料层所占比例的增加，双层碳化硅包壳的失效概率逐渐增加。当表面温度达到峰值时，所有不同厚度比的碳化硅包壳失效概率均达到最大。而在峰值之后，不同厚度比的包壳均呈现先下降后上升的趋势，且随着复合材料层占比越小的包壳失效概率越小。造成这种现象的原因在于复合材料层的热导率远小于单质层的热导率，当包壳表面温度快速变化时，复合材料层占比较大的包壳释放的热量更小，所受的热应力更大，因此失效概率更大。由于CMC层具有非常强的伪塑性，虽然CMC层中热应力较大可能会出现裂纹，但是内部的SiC纤维可以保证包壳的完整性。mSiC材料的致密性较强，且事故情况下产生的温度应力大部分由内部的CMC 材料承担，mSiC 材料发生脆性断裂的概率较小，可以起到包容裂变产物的作用。文献［10-11］也通过模拟论证了mSiC 可以保证包壳的气密性。对于CMC层和mSiC层的最佳厚度比还需要更多地测试。

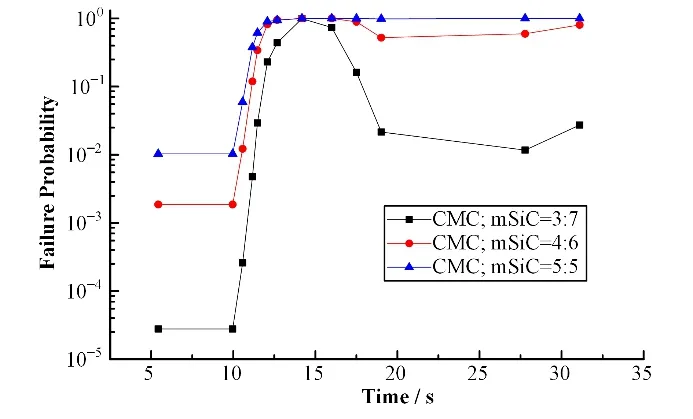
图7 LOCA事故下不同层厚比双层碳化硅包壳瞬态失效概率变化Fig.7 Variation in the transient failure probability of bilayer SiC claddings with different layer thickness ratios under a LOCA

2）Weibull参数敏感性分析

研究了Weibull 参数的选取对于瞬态失效概率的影响，在对参数m和σ0的敏感性计算时，所选参考Weibull 模量m（CVD-SiC）=9.7，m（CMC）=17.5，特征 强 度σ0（CVD-SiC）=250 MPa，σ0（CMC）=290 MPa。分别讨论m±1变化及σ0±10%变化时对包壳失效概率的单因素影响。

图8给出了LOCA工况下双层碳化硅包壳失效概率对m和σ0的敏感性分析结果。可见，无论是m还是σ0，随着参数值的减小，相同时间的包壳失效概率均减小，而随着参数值的增大，包壳失效概率均增大。除此之外，改变m时的包壳失效概率分布曲线变化间距大于改变σ0时的变化曲线，说明在瞬态工况时，包壳失效概率对特征强度σ0的变化相对更敏感。

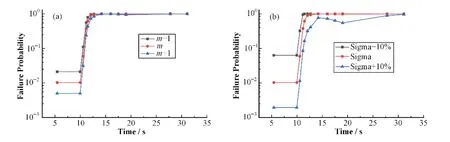
图8 瞬态下双层碳化硅包壳失效概率敏感性分析（5:5） (a) 改变m，(b) 改变σ0Fig.8 Sensitivity analysis of the failure probability of bilayer SiC claddings under transient conditions (5:5)(a) Change in m, (b) Change in σ0

3）线功率对失效概率的影响

此外，讨论了线功率变化对碳化硅包壳失效概率的影响分析。分别选取线功率分别为18 kW·m-1和11.2 kW·m-1，失效概率计算结果如图9 所示。可见，当线功率较低时，包壳失效概率随之降低。并且即使包壳表面温度达到峰值，低线功率对应的包壳失效概率也处在一个较低水平。

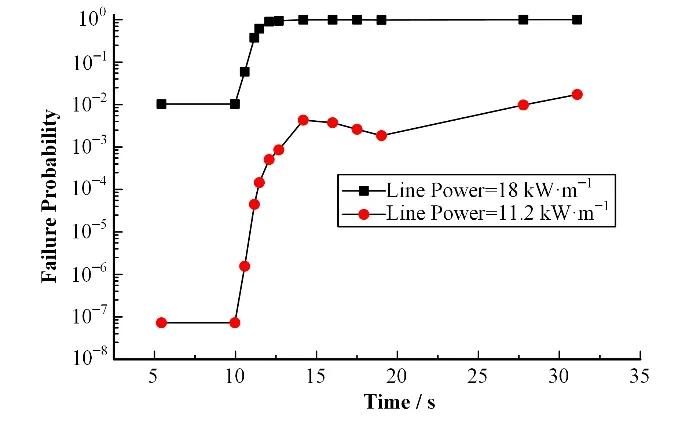
图9 瞬态工况下双层碳化硅包壳失效概率敏感性分析Fig.9 Sensitivity analysis of the failure probability of bilayer SiC claddings under transient conditions

4 结语

本文采用准稳态计算方法，计算得到了LOCA事故下双层碳化硅包壳的失效概率，通过分析模拟结果，得到以下结论：

1）LOCA 事故时，随着包壳表面温度的突然上升，碳化硅包壳失效概率也呈现出快速增大的趋势，随后在内外部压力的共同影响下，失效概率又略有下降，但基本维持不变。

2）由于复合层的导热性能较差，SiC 复合包壳的失效概率会随着复合层占比的增大而增大。

3）在计算双层碳化硅材料包壳瞬态工况下的失效概率时，参数σ0±10%对于失效概率的影响要大于参数m±1的影响，说明在瞬态工况时，包壳失效概率对特征强度σ0的变化相对更敏感。

4）对于较低的线功率，包壳可达到的最高温度会降低，包壳内部的热应力也会相应减小，因此可以降低包壳的失效概率。

作者贡献声明曹力文负责部分仿真计算，初稿撰写；易柏全负责仿真计算；郝祖龙负责课题指导，稿件修改。