LN函数核截面隐式敏感性系数计算方法

胡 馗,马续波,张 辰,刘 莎,陈义学

(华北电力大学 核科学与工程学院,北京 102206)

伴随核能的发展,新的反应堆堆型被不断提出,这些堆型包括铅基快堆、热管堆、空间堆以及混合谱反应堆等。新型反应堆由于工程实践有限及系统自身的反应堆物理特点,导致反应堆物理计算存在较大不确定度。这些物理特点主要指中子能谱较硬,中子主要集中在中高能区,而在中高能区的截面测量误差相对较大,由此导致系统的有效增殖因数的不确定度主要来自于核截面[1]。研究核截面引起的反应堆物理计算的不确定度方法对新型反应堆的设计具有重要意义。

针对核数据引起的反应堆物理计算的不确定度大小,国内外也进行了大量研究,也包括基于最新评价核数据的验证[2],开发了大量的程序,这些程序包括TSUNAMI-1D/3D、SUFR、SCALE-SS、DINOSAUR、MCNP、SURE、UNICORN[3-10]等。敏感性系数的隐式效应与共振自屏截面的处理方法相关,而由于共振自屏计算往往复杂,由此也导致敏感性系数的隐式效应也变得比较复杂。比如针对压水堆问题,可以采用求解连续能谱慢化方程或者改变有效共振积分表的方法考虑隐式效应[11]。针对热堆,由于中子慢化需要经过共振自屏效应强烈的中能区,隐式敏感性效应比较显著,在计算敏感性系数的时候,需要考虑隐式效应。而对于快能谱反应堆(快堆),虽然从理论上讲,隐式效应不是很显著[11],但一直没有很好的方法进行敏感性系数的隐式效应的计算。基于本底截面迭代的共振自屏处理方法在很多反应堆物理程序中都有广泛应用[12],本文针对该共振自屏处理方法提出一种新的隐式敏感性系数计算方法,该方法只需要根据本底截面计算结果就可以计算得到隐式敏感性系数。在此基础上,采用基准题对提出的隐式敏感性系数计算方法进行验证,对比MCNP的计算结果。

1 隐式敏感性系数计算理论

快能谱反应堆截面制作方法有多种,其中一种为利用连续点截面考虑共振自屏制作得到多群截面,然后利用多群截面进行组件或棒栅元计算,考虑几何效应及能谱泄漏影响计算得到多群中子通量密度和中子通量密度矩,或直接进行连续点截面计算中子通量密度或通量矩,然后进行并群得到少群截面,最后进行少群截面的堆芯计算。堆芯计算的响应量相对于少群截面的敏感性系数在之前的相关文献中进行了详细研究[4],但针对组件计算的敏感性系数引入的隐式敏感性则很少,且没有多群相对于连续点截面的相对敏感性系数的计算理论。本文把响应量相对于连续点截面的敏感性系数分为两个部分,分别是多群截面相对于连续点截面的敏感性系数Sσg,σ(E)和响应量相对于多群截面的敏感性系数SR,σg,总的敏感性系数SR,σ(E)计算式为:

SR,σ(E)=SR,σgSσg,σ(E)

(1)

其中:σg为每个能群的平均截面;σ(E)为连续能量点截面。

由于隐式敏感性系数计算与共振自屏截面计算相关,首先讨论多群截面相对于连续点截面的相对敏感性系数。根据反应率守恒,多群截面的计算公式为:

(2)

其中:σx,g(T)为温度为T的第g能群的反应类型为x(x可能是裂变、辐射俘获、弹性散射等)的平均截面;σx(E,T)为反应类型为x的连续点截面;φ(E)为连续能量中子能谱。对于非共振核素,如果对连续点截面做扰动,由于截面并不对能谱形状造成影响,因此,扰动后的截面和扰动前的截面的关系为:

σ′x(E,T)=(1+δx,g)σx(E,T)

Eg≤E≤Eg-1

(3)

(1+δx,g)σx,g(T)

(4)

其中:δx,g为群截面的扰动量,一般为1%[11];ΔEg为g能群的能群宽度。由于温度在共振自屏处理前已处理完成,为叙述方便,下面的公式推导均在给定温度下进行,不再标温度T。由式(5)可见,相当于直接对超细群截面的每个能群做扰动。如果对于共振核素,在窄共振近似下,中子能谱可表示为:

(5)

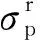
(1+δx,g)σx,g(σ′0)

(6)

其中,δt,g为由于x截面的扰动而造成总截面的扰动量。截面随本底截面的变化规律类似于LN函数[13],如采用LN函数对本底截面进行插值,则为:

σx,g(σ1)=Aglnσ0+Bg

(7)

其中,

(8)

由于正扰动和负扰动计算超细群截面相对于连续点截面的隐式敏感性系数Sσg,σ(E)为:

(9)

(10)

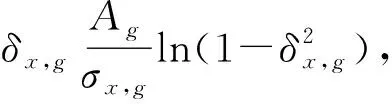
2 计算流程

利用式(9)、(10)进行敏感性系数和不确定度计算的流程如图1所示。由图1可见,多群截面的相对于连续点截面的敏感性系数可根据本底截面的计算结果给出,然后再与扰动多群截面得到的敏感性系数一起,即可计算得到总的敏感性系数。在不确定度分析程序SUFR中增加了对多群截面扰动功能,扰动后的截面再用MGGC2.0中一致性PN方法或其他堆芯程序计算系统的有效增殖因数。另外在截面处理程序中增加了计算隐式敏感性系数中Cg参数的模块,通过此模块计算多群截面相对于连续点截面的敏感性系数。

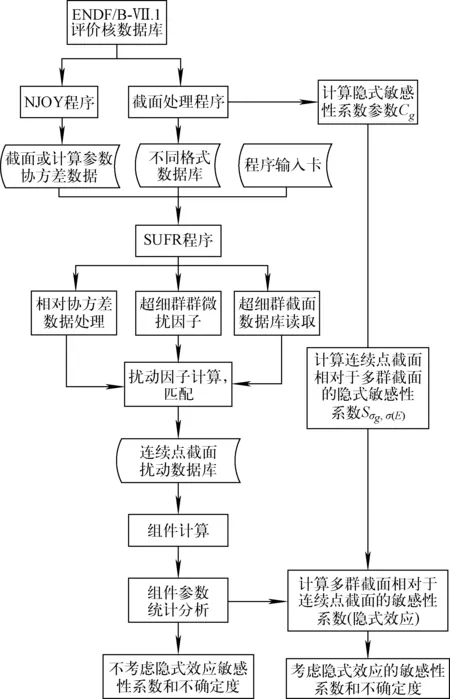
图1 少群截面的敏感性系数的计算流程Fig.1 Calculation process of sensitivity coefficient for few-group cross-section

3 计算结果

为计算隐式敏感性,采用一无限大基准题模型,基准题模型中仅包括了对快能谱反应堆不确定度分析具有重要影响的6种核素(表1)。计算软件采用了截面处理软件MGGC2.0[14-15]或堆芯计算软件。MGGC2.0程序是一款专门为快谱或混合谱反应堆制作少群截面的软件,通过求解超细群的输运方程计算中子通量密度和中子通量密度矩,然后进行并群得到少群截面。MGGC2.0中采用了求解一致性PN方程加上临界搜索的方法求解反应堆堆芯中子能谱,利用本底截面迭代的方法求解有效自屏截面。

表1 基准题核子密度Table 1 Atomic density of isotopes in benchmark

3.1 多群截面隐式敏感性系数

共振自屏效应是反应物理计算中的重点,NJOY2016在制作多群截面时,采用了随温度和本底截面σ0变化的截面。使用时,可采用各种方法求解与几何和核素相关的本底截面σ0,然后再去之前的截面本底网格中插值得到问题相关的有效自屏截面。在敏感性分析中,由于某核素截面发生变化,导致中子能谱发生变化,进而引起敏感性系数发生变化称为隐式敏感性。本文把能谱变化与本底截面σ0联系起来,进而计算截面隐式敏感性。具体实施步骤为:首先利用NJOY2016程序制作了超细群(2 082能群)的MATXS格式多群截面,多群截面随温度和本底截面变化,温度选取了300、600、900、1 200、1 500、1 800、2 100 K共7个温度点,本底截面选取1.0×1010、1.0×107、1.0×105、1.0×104、1.0×103、1.0×102、10、1.0、5.0×10-1、1.0×10-1b,共10个本底截面。MGGC2.0针对所研究的问题进行本底截面迭代,计算式(10)中的Ag和σx,g(T,σ0),然后利用式(9)可计算得到核素每个反应道的每个超细群的敏感性系数。图2～5分别给出了239Pu、238U、56Fe和23Na的超细群有效共振自屏截面和相应的每个反应道每个能群截面的相对敏感性系数Sx,g。

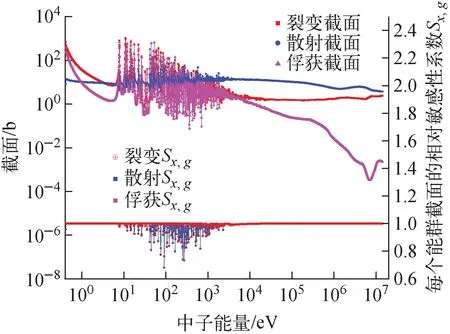
图2 239Pu核素有效共振自屏截面和相对于连续点截面的敏感性系数Sx,gFig.2 Effective self-shielding cross-section of 239 Pu and its sensitivity coefficient respect to continue cross-sections Sx,g

图3 238U核素有效共振自屏截面和相对于连续点截面的敏感性系数Sx,gFig.3 Effective self-shielding cross-section of 238U and its sensitivity coefficient respect to continue cross-sections Sx,g

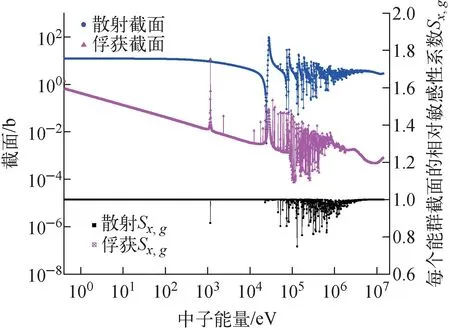
图4 56Fe核素有效共振自屏截面和相对于连续点截面的敏感性系数Sx,gFig.4 Effective self-shielding cross-section of 56Fe and its sensitivity coefficient respect to continue cross-sections Sx,g

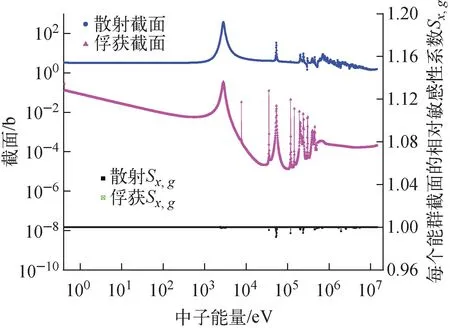
图5 23Na核素有效共振自屏截面和相对于连续点截面的敏感性系数Sx,gFig.5 Effective self-shielding cross-section of 23Na and its sensitivity coefficient respect to continue cross-sections Sx,g

由图2可见,在没有共振的能量区间,每个能群截面的相对敏感性系数等于1.0。在共振峰密集的能群区间,每个能群截面的相对敏感性系数Sx,g均在1.0附近,能群截面的相对敏感性系数均明显小于1,最大的可到0.7。由于能群截面的相对敏感性系数在共振的能区明显小于1,这样将会使得考虑隐式敏感性系数后,响应量相对于超细群的敏感性系数会减小。由于每个核素的共振能区的位置不一样,每个超细群相对敏感性变化明显的能区也有明显差别,如239Pu和238U变化较明显的能区在10～10 000 eV,但56Fe的变化较明显的能区为104～107eV,主要是因为56Fe的共振峰集中在这个能量区间。但对于23Na,在共振能区,能群截面的相对敏感性系数较56Fe要更接近1.0。由于是超细群能群结构,23Na的共振峰均能很好地被描述,在超细群的共振峰内部,共振自屏效应较弱。这也说明,共振自屏的强弱跟能群结构也有很大关系,如果能群宽度越宽,每个能群中包括的共振峰数目越多,则该能群的共振自屏效应越强。

3.2 考虑隐式效应的keff敏感性系数

前面计算得到每个核素每个反应道每个能群的相对敏感性系数可应用于任何响应量。为验证前面计算的每个能群截面的相对敏感性系数的正确性,选用有限增殖因数作为响应量,计算keff相对于多群以及少群截面的相对敏感性系数,采用了MCNP连续点截面计算的结果作为基准。MCNP程序计算基于ENDF/B-Ⅶ.1,每代粒子数为100 000个,粒子代数为400代,舍掉前100代。

不考虑隐式效应的keff相对敏感性系数计算方法:利用NJOY程序制作得到多群MATXS格式数据库,采用MGGC2.0通过本底截面迭代计算得到各个核素的不同反应道的有效自屏截面,然后利用SUFR程序对每个多群分别进行正负扰动,然后再利用MGGC2.0或堆芯计算程序做输运计算,得到系统的keff相对于每个核素每个细群的相对敏感性系数SR,σg。利用响应量相对于每个细群的相对敏感性系数SR ,σg以及式(9)计算得到多群相对于连续点截面的相对敏感性系数Sσg,σ(E),两者相乘可得到考虑隐式效应的细群的敏感性系数。考虑隐式效应和不考虑隐式效应两种情况的少群敏感性系数计算公式分别为式(11)、(12)。

(11)

(12)

图6～10分别给出了238U辐射俘获、239Pu裂变、239Pu辐射俘获、56Fe辐射俘获和23Na辐射俘获反应道少群截面keff的相对敏感性系数。由图6～10可见,考虑隐式效应的细群的相对敏感性系数与不考虑隐式效应的细群的相对敏感性系数随能量的变化趋势与MCNP的计算结果吻合较好,细群相对于连续点截面的相对敏感性系数Sσg,σ(E)对细群相对于keff的相对敏感性系数起到了修正的作用。这种修正作用对于不同核素,作用的能群位置和大小也会有所变化。为更清楚表示隐式效应的修正作用,表2给出了少群截面相对于keff的总敏感性系数对比。由表2可见,除239Pu裂变反应道,考虑隐式敏感性系数后的结果与MCNP吻合更好,少群截面相对于keff的总敏感性系数均有明显改进。对于239Pu裂变反应道,由图7可见,不考虑隐式效应的敏感性系数本身均较MCNP计算结果偏低,而隐式效应的修正进一步使原来的敏感性系数更低,所以相比于MCNP的结果偏离方向与其他计算结果稍有不同,该偏离方向可能跟不同反应道的共振自屏效应不同,而Bondarenko本底截面方法中只对总截面迭代,由此可能造成不精确,有待进一步研究分析。

表2 少群截面相对于keff的总的敏感性系数对比Table 2 Comparison of total sensitivity coefficients respect to keff for different isotopes

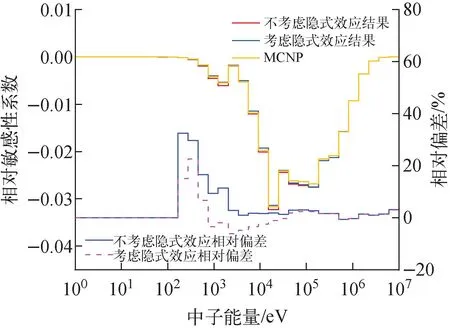
图6 238U辐射俘获反应道少群keff的相对敏感性系数Fig.6 Relative sensitivity coefficients of keff of 238U capture

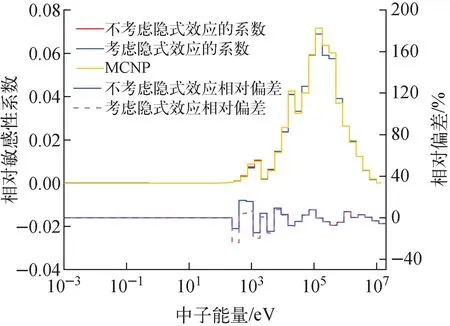
图7 239Pu裂变反应道少群keff的相对敏感性系数Fig.7 Relative sensitivity coefficients of keff of 239Pu fission

图8 239Pu辐射俘获反应道少群keff的相对敏感性系数Fig.8 Relative sensitivity coefficients of keff of 239Pu capture

图9 56Fe辐射俘获反应道少群keff的相对敏感性系数Fig.9 Relative sensitivity coefficients of keff of 56Fe capture

图10 23Na辐射俘获反应道少群keff的相对敏感性系数Fig.10 Relative sensitivity coefficients of keff of 23Na capture

3.3 不确定度计算

利用少群的敏感性系数计算上述反应道的keff的不确定度大小,对比考虑隐式敏感性与不考虑隐式敏感性的差别。不确定度的计算方法:将并群得到的考虑隐式敏感性和不考虑隐式敏感性的相对敏感性系数,利用式(13)计算得到keff响应量的不确定度,比较结果以MCNP为基准。本模拟中采用了每代10 000个例子,活跃带为300代,非活跃带为100代,keff=1.465 08,统计误差为0.000 23。

(13)

表3 不同反应道相对于keff的不确定度Table 3 Comparison of total uncertainty of keff for different isotopes

4 结论

为更精确计算核截面数据引起的反应堆物理计算结果的不确定度,提出了一种新的隐式敏感性系数计算方法。利用该方法可计算多群截面相对于连续点截面的敏感性系数,进而考虑截面的隐式效应。并通过基准题对本文提出的隐式效应敏感性系数计算方法进行验证,采用MCNP计算结果作为基准解,分析响应量keff的计算结果,238U辐射俘获、239Pu辐射俘获、56Fe辐射俘获和23Na辐射俘获反应道的结果显示:考虑隐式效应的多群的相对敏感性系数与不考虑隐式效应的细群的相对敏感性系数随能量的变化趋势跟MCNP的计算结果基本一致,可显著改善相对敏感性系数的计算精度。采用多群截面计算,在共振自屏效应强烈的能群,隐式效应修正最大可达50%。针对少能群截面,考虑隐式效应与不考虑隐式效应计算得到的keff总相对敏感性系数和不确定度均有明显提升。以上计算结果说明了本文提出的隐式敏感性系数计算方法的可行性。

针对239Pu裂变反应,改进不明显可能跟Bondarenko本底截面迭代处理共振自屏方法本身有关。在Bondarenko方法中,为考虑共振自屏对中子能谱的影响,需根据实际核素成分和几何计算出本底截面,然后再去总截面网格中插值进行本底截面迭代,一直到总截面收敛。该方法的明显缺点是,不同反应道的共振自屏可能不一样,传统的Bondarenko本底截面只对总截面做迭代,而不对其他反应道处理,这样就有可能导致利用总截面迭代出来的共振自屏因子对应用于其他反应道时,可能会造成一定偏差。但通过总截面的本底截面迭代虽不能对所有核素所有反应道均能较好考虑共振自屏,但对大多数核素的主要反应道,计算结果有所改善。若要精确计算,将来需进行连续点截面才能更好考虑共振自屏效应和灵敏度系数的隐式效应。