基于分子干涉函数的光子-原子相干散射截面计算方法研究

徐 宁,祖铁军,曹良志,吴宏春

(西安交通大学 核科学与技术学院,陕西 西安 710049)

光子在核能系统中有着重要的应用。在核反应堆释热计算[1]和辐射屏蔽计算[2]中需要考虑光子影响,同时,在材料无损检测和医学散射成像领域,X射线衍射也有着重要应用[3]。X射线衍射的基本物理原理为光子与物质发生相干散射,为了实现对于X射线衍射过程的数值模拟,需要提供精确的光子-原子相干散射截面。

光子与原子发生相互作用时,原子核外的电子在电磁场的作用下产生受迫振动,电子的受迫振动会产生一个与入射光子频率相同的交变电磁场,该交变电磁场会向周围辐射与入射光子频率相同的次级光子。由于次级光子频率相同,且具有固定的相位差,彼此之间会产生相互干涉,因此光子与原子发生的上述相互作用过程称为相干散射,也称为瑞利散射。相干散射产生的次级光子与入射光子具有相同的频率,反应前后光子的能量不会发生改变,仅光子的方向改变,因此相干散射也是弹性散射过程。

传统的相干散射微分截面计算采用独立原子形状因子近似方法[4]修正Thomson散射截面,该方法可精确计算光子动量转移较大时的相干散射微分截面[5]。当光子动量转移较小时,采用上述假设会导致相干散射微分截面的计算存在较大偏差,无法准确描述相干散射次级光子的角度分布。因此,对于上述情况光子相干散射微分截面的计算,需要采用更加准确的计算方法。

本文在传统的独立原子形状因子近似的基础上,通过考虑分子干涉效应将传统的相干散射微分截面计算方法拓展至光子动量转移较小的场景,可实现对于全能量段光子相干散射微分截面的准确计算。同时,将修正后的原子形状因子应用于蒙特卡罗程序,对比分析采用独立原子形状因子近似方法和采用分子干涉函数修正后的原子形状因子对相干散射次级光子角度分布的影响。

1 相干散射截面计算方法

1.1 独立原子形状因子近似

光子与1个自由电子的弹性散射截面可由Thomson散射公式表示:

(1)

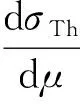
不同于Thomson散射公式描述的光子与1个自由电子的弹性散射过程,原子核外的电子会受到原子核对核外电子的束缚,不同轨道上的电子能量存在差异,即原子核外的电子存在电子密度分布;同时对于除了氢元素以外的其他元素,其中性原子的原子核外都存在不止1个电子[6]。基于以上两种原因,无法直接采用Thomson散射公式对相干散射截面进行计算,需要对其进行修正以考虑上述两个因素的影响。目前,比较常用的修正方法为独立原子形状因子近似方法。

对于1个孤立原子,其原子核外电子分布不受其他原子核外电子分布影响,假设其原子核外电子密度分布为球形对称分布,此时相干散射微分截面可表示为:

(2)

动量转移x可表示为:

(3)

式中:θ为散射角度;me为电子静止质量;h为普朗克常数;c为光速;k为以电子静止能量为单位的入射光子能量;λ为入射光子波长;E为入射光子能量。

采用独立原子形状因子近似修正Thomson散射截面仅可考虑孤立原子内部的电子密度分布对相干散射微分截面的影响,忽略了分子内干涉效应和分子间干涉效应对相干散射微分截面的影响。基于独立原子形状因子近似方法计算分子的相干散射微分截面时只需要对分子中各原子的微分散射截面按照核子密度加权即可[7]。

(4)

该近似方法仅适用于当光子动量转移较大时的相干散射微分截面计算,当光子动量转移较小时,忽略分子内和分子间干涉效应将会对相干散射次级光子角度分布的计算精度产生影响。

1.2 分子干涉函数计算

分子干涉效应可分为分子内部干涉效应和分子间干涉效应。对于分子内部干涉效应可采用Debye公式计算。考虑分子内部干涉效应的原子形状因子为:

(5)

式中:FDebye(x)为采用Debye公式计算的原子形状因子;fj(x,Zj)为元素j的独立原子形状因子;rij为分子内元素i和j之间的距离。

对于分子间干涉效应一般采用分子干涉函数进行修正,分子干涉函数S(x)[8]可表示为:

(6)

式中,sij(x)为局部分子干涉函数。

在已知分子结构的情况下,局部分子干涉函数可通过分子动力学模拟进行计算[9]。

(7)

式中:ρ0为原子数密度,即单位体积内的原子数;gij(r)为径向分布函数,表示在1个参考原子i周围距离为r处,原子类型为j的原子在dr厚度的球壳内的局部密度相对于参考原子数密度的比值。

考虑分子内部干涉效应和分子间干涉效应的原子形状因子F(x)可表示为:

F(x)=

(8)

采用式(8)计算得到的原子形状因子修正Thomson散射截面可以得到考虑分子干涉效应的光子-原子相干散射微分截面:

(9)

1.3 分子干涉效应在蒙特卡罗程序中的实现

在蒙特卡罗程序中,相干散射微分截面[10]可表示为:

(10)

式中:p(μ)为相干散射次级光子角度分布;re为电子半径。

为了获得合适的概率密度分布,将式(10)中对μ的微分转化为x2的微分:

(11)

由式(11)可知,在蒙特卡罗程序中进行相干散射模拟时,需要光子-原子ACE格式数据库中提供的独立原子形状因子f(x,Z)和积分原子形状因子A(x2,Z)。基于独立原子形状因子近似计算的积分原子形状因子可表示为:

(12)

当考虑分子干涉效应时,需要利用分子干涉函数对原子形状因子进行修正,考虑分子干涉函数的原子形状因子可表示为:

F2(x,Z)=S(x)f2(x,Z)

(13)

将考虑分子干涉效应的原子形状因子代入式(10)和式(11)可得到考虑分子干涉效应的原子形状因子FMI(x,Z)和积分原子形状因子AMI(x2,Z):

(14)

(15)

基于式(14)和式(15)对ACE格式数据库中需要的原子形状因子和积分原子形状因子进行计算,得到考虑分子干涉效应的光子-原子ACE格式数据库。

2 数值结果与验证

2.1 分子干涉函数计算

对于结构参数已知的分子,其分子干涉函数可通过分子动力学模拟程序进行计算。本文分别针对水分子和乙醇分子进行分子动力学模拟,获得各原子之间的径向分布函数,其中,水分子采用TIP4P/2005模型[11],乙醇分子采用Loren William模型[12]。对于水分子和乙醇分子在模拟过程中均采用OPLS-AA力场,利用GROMACS分子动力学程序[13]分别对水分子和乙醇分子进行模拟,获得水分子和乙醇分子各原子间的径向分布函数,如图1所示。

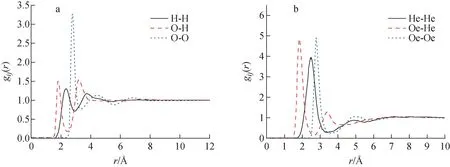
图1 水分子(a)和乙醇分子(b)中各原子间的径向分布函数Fig.1 Radial distribution function of water (a) and ethanol (b)

基于图1计算得到的水分子和乙醇分子的径向分布函数,利用式(7)可计算得到水分子和乙醇分子的局部分子干涉函数,如图2所示。最后,对局部分子干涉函数进行加权计算,可得到水分子和乙醇分子的分子干涉函数,如图3所示。其中,将水分子的分子干涉函数模拟结果与实验测量结果[14-18]进行对比,可看出基于分子动力学模拟获得的水分子的分子干涉函数与实验测量结果吻合较好,可以用于修正独立原子形状因子,获得考虑分子干涉效应的原子形状因子。

图2 水分子(a)和乙醇分子(b)的局部分子干涉函数Fig.2 Partial molecular interference function of water (a) and ethanol (b)

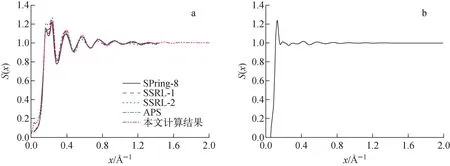
图3 水分子(a)和乙醇分子(b)的分子干涉函数Fig.3 Molecular interference function of water (a) and ethanol (b)

将模拟计算得到的水分子和乙醇分子的分子干涉函数分别修正,基于独立原子形状因子近似方法给出的水分子和乙醇分子中各元素的原子形状因子,可得到上述两种分子中各元素考虑分子干涉效应的原子形状因子,如图4、5所示。

图4 水分子中H元素(a)和O元素(b)基于独立原子形状因子近似和考虑分子干涉效应的原子形状因子Fig.4 Independent atomic form factor approximation and atomic form factor modified by molecular interference effect of H (a) and O (b) elements of water

图5 乙醇分子中C元素(a)、H元素(b)和O元素(c)基于独立原子形状因子近似和考虑分子干涉效应的原子形状因子Fig.5 Independent atomic form factor approximation and atomic form factor modified by molecular interference effect of C (a), H (b) and O (c) elements of ethanol

2.2 分子干涉效应对相干散射角度分布的影响分析

为了验证分子干涉效应对相干散射角度分布的影响,本文分别制作了采用独立原子形状因子近似和考虑分子干涉效应的光子-原子ACE格式数据库,利用蒙特卡罗程序对图6所示装置进行了模拟,并对水和乙醇的成像效果进行了对比分析。图6装置中的光子源S采用管电压为100 kV的X射线管,其光子源能谱如图7所示,光子源距离样品中心的距离SAD为100 cm,光子源距离探测板W的距离SDD为153.6 cm,样品为0.5 cm×0.5 cm×0.5 cm的立方体,探测板宽度为41 cm[19]。

图6 成像装置示意图[19]Fig.6 Illustration of imaging geometry[19]

图7 光子源能谱Fig.7 Spectrum of photon source

图8示出采用独立原子形状因子近似和考虑分子干涉效应的水分子散射成像模拟结果与Poludniowski等[19]计算结果的对比。由图8可看出,基于本文计算得到的分子干涉函数计算得到的水分子成像结果与Poludniowski等的计算结果吻合较好。通过图8的对比分析可发现,考虑分子干涉效应模拟得到的水分子散射成像在光子动量转移较小时与采用独立原子形状因子近似模拟得到的结果存在明显的差异。对于光子与水分子散射成像结果可看出,考虑分子干涉效应会导致相干散射的前向散射显著减少。图9示出本文模拟得到的乙醇分子的散射成像模拟结果,由图9的结果对比可得出与水分子散射成像模拟相同的结论,即考虑分子干涉效应时,相干散射的前向散射明显减少。

图8 采用独立原子形状因子近似(a)和考虑分子干涉效应(b)的水分子响应信号对比Fig.8 Comparison of scattering image of water using independent atom form factor approximation (a) and molecular interference effect (b)

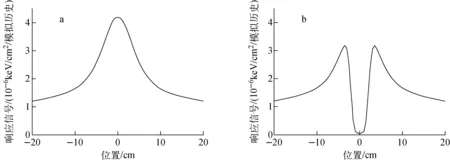
图9 采用独立原子形状因子近似(a)和考虑分子干涉效应(b)的乙醇分子响应信号对比Fig.9 Comparison of scattering image of ethanol using independent atom form factor approximation (a) and molecular interference effect (b)

3 结论

本文介绍了基于独立原子形状因子近似的传统相干散射截面计算方法,同时为了实现对于X射线衍射的数值模拟,本文介绍了考虑分子干涉效应的相干散射截面计算方法。基于分子动力学模拟获得了水分子和乙醇分子的分子干涉函数,对光子-原子ACE格式数据库中相应数据进行了修正,并利用蒙特卡罗程序对水分子和乙醇分子的散射成像效果进行了数值模拟。数值结果显示,对于水分子和乙醇分子,考虑分子干涉效应会导致光子的前向散射显著减少。