砂土中冲刷条件下三筒基础水平承载特性研究

赵学亮，王 鑫，陈馨睿，隋淑环，沈侃敏，邓温妮

（1.东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 211189；2.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122）

吸力式筒型基础作为深海油气平台的一种基础形式，近年来逐渐在海上风电领域得到推广应用，相比传统海上风机基础，具有施工安装方便、无噪音、可重复利用、方便拆除等优点。吸力式多筒基础在较深海域能表现出更好的安全性和经济性，可适用于水深20～40 m甚至更深的海域，拥有广阔的发展前景。在海上波浪流的作用下，吸力式筒基础周围流场发生变化，顶部附近海床易发生局部冲刷从而降低吸力式筒基础入土深度，导致基础承载力受到影响。近年来随着吸力式筒型基础的推广和应用，冲刷对筒型基础承载性能的影响受到越来越多的关注。

鲁晓兵等［1］认为同种砂土地基中，筒型基础的直径、筒高以及在地基中的埋深直接影响其承载特性，其他学者们也大都以筒高、筒径和基础埋深作为影响因素来研究筒基的位移模式和极限承载力等受冲刷的影响［2-4］。海上风电基础在工作时受到波浪流的冲刷，易出现失稳破坏，Chen 等［5］对整体冲刷下筒型基础的稳定性进行试验研究，结果表明基础的稳定性随着冲刷深度的增加逐渐降低，基础的最终状态逐渐从循环稳定转变为循环失效。马天驰等［6］对整体冲刷作用下吸力筒基础的位移模式、筒顶位移和转动点进行小比尺模型试验，认为在波浪循环荷载作用下，整体冲刷作用对筒基础运动模式的影响不大，但整体冲刷深度对筒顶位移影响极大。Liu等［7］通过试验分析了冲刷条件下筒型基础在波浪和水流作用下的循环响应，并提出了计算冲刷作用下筒型基础转角的经验公式。

为研究各冲刷条件下的极限承载力，陆罗观等［8］引入冲刷率的概念，采用有限元方法研究不同冲刷率下复合筒型基础的竖向极限承载力，并基于Meyerhof 理论计算不同冲刷率下筒型基础的竖向极限承载力。Zhu 等［9］考虑了冲刷土体应力历史的影响，计算整体冲刷条件下的筒型基础竖向承载力。张鹏辉［10］对长径比在0.25～2.00之间的筒型基础进行复合加载承载特性模拟，分析了不同长径比的筒基在不同冲刷条件下的承载力演化规律及破坏机制。

吸力式筒型基础在工作中主要承受自重带来的竖向荷载和波浪、海流所引起的水平与弯矩荷载的复合荷载。基础失稳破坏时所受各种荷载的分量组合在应力空间内构成一个三维极限状态曲线，即极限荷载包络图。Palix 等［11］、Kay 和Palix［12］结合不同的有限元软件，提出了沉箱基础在黏土中的V-H-M包络线的有限元计算方法。Hung和kim［13］、刘润等［14］通过有限元分析筒型基础在V-H、V-M、H-M和V-H-M加载模式下的地基承载力包络线，并提出筒形基础的修正承载力表达式。V-H-M包络线表明，随着竖向承载力增加，筒基础的水平承载力和抗倾覆能力降低。但是对小于竖向极限承载力40%的垂直荷载，给定的竖向荷载对水平和抗倾覆组合承载力的下降可以忽略不计，在实际中筒基础的竖向承载力远小于竖向极限承载力的40%［15］。

对于吸力式三筒基础承载力，目前研究较少。Kim等［16］利用有限元分析三筒基础的间距、嵌入深度和荷载方向对承载力的影响，并提出三筒基础承载力的修正参数；乐丛欢等［17］基于有限元分析四筒导管架基础的筒径与筒高对基础抗弯承载力的影响；Li等［18］采用数值模拟分析四筒基础周围的冲刷模式对地基承载包络线的影响。

三筒基础因具有较大直径，能有效承受基础上部结构自重传递至基础的竖向荷载，筒与筒之间的组合效应，使其水平和抗弯承载力大大提高，但因筒型基础相较桩基础埋深浅，冲刷对其承载力的影响更应得到重视。目前考虑冲刷作用的吸力式多筒基础承载力变化分析研究尚不充足。因此，这里采用模型试验和数值模拟方法，分析冲刷作用对三筒基础的水平和弯矩承载力的影响，提出冲刷条件下三筒基础的水平和弯矩极限承载力计算方法。

1 模型试验研究

研究通过小比尺模型试验，对不同冲刷条件下的三筒基础进行一定加载高度的水平加载试验，研究冲刷条件下三筒基础的水平承载性能。

1.1 试验方法

将吸力筒视为刚性基础，采用钢材制作吸力筒模型。3 个模型筒尺寸一致，长度L为150 mm，顶盖厚度δ1为5 mm，外径Do为120 mm，内径Di为117 mm，长径比为1.25，筒壁壁厚δ2取1.5 mm。结合文献［19］中对模型试验边界范围的研究，水平荷载对吸力筒周围2.5 倍筒直径范围外、荷载方向后侧土体几乎没有影响，基于本试验所用模型筒的尺寸，制作尺寸为1.2 m×1.2 m×1.5 m（长×宽×高）的模型箱，以避免三筒基础周围土体的边界效应对试验结果的影响。试验布置如图1所示。

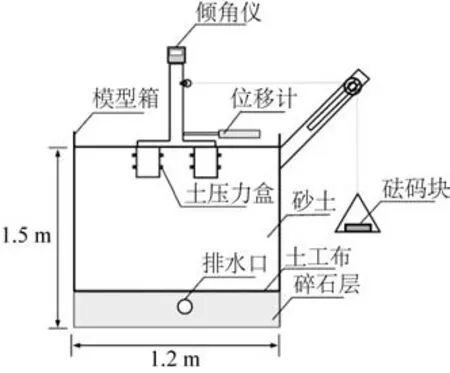
图1 试验布置示意Fig.1 The layout of a model test

试验所用砂土为级配良好的中密砂，砂土的基本物理力学性质见表1，颗粒级配曲线如图2 所示。模型试验开始前向试验箱内分层填筑砂土并夯击，施加0.45 N/mm2的作用力进行预压。48 h后向模型箱内注水，待模型箱底部排水口有水流出后关闭排水口，水高过泥面后停止注水，并静置24 h 使之固结。为方便观察试验现象，试验开始前，所有水排出试验箱，所以本试验采用的是完全饱和砂土，综合考虑了实际工程中水的影响。

表1 试验用砂物理参数Tab.1 Physical parameters of test sand

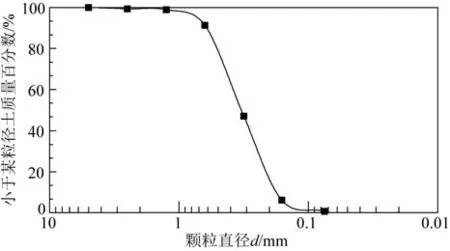
图2 模型试验所用砂土粒径级配曲线Fig.2 The grain size distribution curve of test sand

为了模拟冲刷条件，试验中将对筒周土体进行开挖，对于冲刷坑开挖形态，通过对吸力筒冲刷特征进行物理模型试验研究来考虑，为此分别开展了不同波流条件下（入射波高hw=0.05～0.15 m，周期T=1.0～1.8 s，水流速度Uc=0.26～0.31 m/s），不同结构尺寸的单筒与三筒基础的冲刷水槽试验（单个筒基础的直径为30 cm）。图3（a）为水槽现场图片，图3（b）为测量流场特点使用的传感器（波高仪、流速仪），图3（c）～（f）为吸力筒单筒与多筒模型。

图3 水槽、仪器和模型筒Fig.3 Flume, instrument and bucket modes

水槽中冲刷试验布置如图4 所示。筒型基础的冲刷坑形态为前半侧圆环状冲刷、后半侧为“人”字形淤积，如图5（a）所示。测量各个筒基础在不同波浪水流条件下的局部冲刷坑深度与宽度，如图5（b）所示，冲刷深度d和冲刷宽度w可以简化为线性关系，见式（1）。已有学者通过对单筒基础的承载力进行研究认为，筒型基础的水平承载力主要由筒内土体和荷载方向前侧的土体提供［20］，后侧土体的冲刷对承载力影响不大，因此开挖冲刷坑时考虑波浪的方向性及最不利承载工况，忽略筒后少量淤积。为简化冲刷坑形态以更好地量化控制冲刷条件，同时最大程度上模拟冲刷坑对承载特性的影响，本试验在开挖冲刷坑时将以倒圆锥台作为冲刷坑形状，如图5（c）所示。

图4 冲刷试验布置示意Fig.4 Scour experiment setup

图5 水槽冲刷形态及开挖形态Fig.5 Scouring patterns and excavation forms in water channels

式中：d为冲刷坑深度；w为冲刷坑宽度。

1.2 试验工况

研究内容为不同冲刷条件下，不同尺寸三筒基础的水平和弯矩承载性能，因此在设计试验工况时，主要控制冲刷率e、相对筒间距S/D（S为各筒中心点之间的距离，D为筒直径）这两个因素。其中冲刷率e的定义为冲刷深度ds和吸力筒直径D的比值。

相比单筒基础，三筒基础和筒间土相互作用提高了基础的承载力［21］。根据文献［22］结果，考虑承载力增长率和用钢量增长率的平衡问题，三筒基础最佳优化尺寸为L/D=1.27、S/D=3，长径比与本试验模型筒的长径比1.25 非常接近，故本试验设置三筒基础的相对筒间距S/D=3。当筒型基础上部结构与主筒直径比值介于0.2～0.5 时，该基础具有一定的防冲刷能力，因此筒基础周围的冲刷深度较小［23］。结合三筒基础的冲刷试验结果，各工况筒周最大冲刷深度的范围在0.08D～0.49D之间，因此设置试验承载力模拟的冲刷率e分别为0、0.2、0.4、0.6，共4组试验，详见表2。

表2 水平承载力试验工况Tab.2 Test conditions of horizontal bearing capacity

试验采用恒载加载方式，通过添加砝码块逐步施加水平荷载。根据《港口工程桩基规范》（JS 167—4—2012）对水平静荷载试验的规定，加载时荷载级差取预估荷载的1/10左右，每级加载至少维持5 min，观察筒顶放置的位移计，待筒体稳定后再施加下一级荷载。在加到某一级荷载时，筒体的水平位移快速增大，在荷载不变的前提下，位移持续变大并没有减缓的趋势，停止加载。在饱和砂土中采用水平分级加载的方法，每级加载之间间隔时间较长，属于慢加载，砂土渗流性好，采用慢加载有足够时间进行排水，该试验中分级加载时间是5 min，该模型定义为排水行为［16］。

1.3 试验结果分析

针对相对筒间距S/D为3的三筒基础进行不同冲刷率下的水平加载试验，水平加载高度He为360 mm，如图6所示为三筒基础失稳过程。通过观察分析试验过程，可将三筒基础加载过程分为3个阶段：弹性变形阶段—塑性变形阶段—失稳破坏阶段。弹性变形阶段三筒基础的位移非常微小，难以观察，筒顶位移计监测所得数据小于1 mm；但随着荷载逐级增加，在受拉筒后侧可观察到筒壁与土体分离产生的微小缝隙，对应于图7曲线初始阶段，三筒基础基本没有位移发生。随着水平荷载加大，三筒基础周围的土体逐渐从弹性变形阶段进入塑性变形阶段，受压筒前侧土体逐渐被拱起，产生向外扩散的细小裂缝，受拉筒后侧裂缝逐渐扩大，筒体开始产生向上拔起、向荷载方向转动的趋势，对应于图7 曲线开始发生位移阶段。当施加最后一级荷载后，基础进入失稳破坏阶段，水平荷载保持不变的情况下，基础变形开始快速增长，直至倾倒，对应于图7曲线位移剧烈发生阶段。

图6 冲刷率e=0.2时基础失稳过程Fig.6 Process of foundation failure with scour rate e=0.2

图7 不同冲刷率下荷载—位移曲线Fig.7 Load-displacement curves with different scour rate

从图6（b）可以看出：基础破坏时，受压筒和受拉筒前侧土体均被挤压形成楔形破坏区，说明受拉筒和受压筒前侧的被动土压力为三筒基础提供了部分水平承载力。受拉筒被完全拔出时，可以观察到受拉筒内土体脱落，说明筒内土体与筒壁在加载过程中发生摩擦，进一步说明受拉筒提供的水平承载力部分来自筒壁内外侧与土体的摩擦。

图7为不同工况的荷载—位移曲线，采用切线相交法计算得到冲刷率e分别为0、0.2、0.4时，三筒基础的水平极限承载力分别为378、329 和316 N，水平承载力随冲刷率提高而下降。受试验组数限制，下面将建立有限元模型，详细分析冲刷对三筒基础承载性能的影响效果。

2 冲刷对水平和弯矩承载特性影响

为进一步研究冲刷对水平和抗弯承载力的影响，建立有限元模型对模型试验进行验证并扩展分析。

2.1 有限元模型建立与验证

数值模型中吸力筒的尺寸取值与模型试验中取值一致。为了简化模型以提高计算效率，三筒基础各筒顶之间通过设置梁单元进行刚性连接。实际工程中的三筒基础在XY平面上一般为等边三角形分布形式，将该等边三角形几何中心处作为荷载施加点。界面强度折减系数Rinter反映筒土相互作用程度，范围在0～1之间，一般情况下和周围完整土体相比，接触面强度低、刚度小。强度折减系数值取决于结构材料和土层材料的特征（接触面的粗糙程度），无相关经验和数据的情况下可按照2/3输入，这里定义界面系数Rinter=0.67。

筒体材料采用Q235 钢材，定义筒为线弹性本构模型，取弹性模量Ns=2.06×105MPa，泊松比v=0.31，筒的重度γ=78.5 kN/m3。采用Mohr-Coulomb 模型模拟砂土的应力应变关系，土体材料的参数取值与模型试验用砂参数基本一致。但在设置黏聚力时，若黏聚力为0会使计算结果偏小，Brinkgreve推荐黏聚力c=0.2 kPa、剪胀角ψ=4°［24］，数值模拟参数设置见表3。

表3 有限元模型物理参数Tab.3 Physical parameters of finite element models

三筒基础在3倍筒间距S水平方向、2倍筒长L竖直方向以及筒基础内部土体进行局部网格加密，设置粗糙系数为0.35，对于其他部分的模型进行单元网格自适应划分，如图8所示。

图8 有限元计算模型Fig.8 The model of the finite element method

图9为试验和模拟所得不同冲刷条件下三筒基础的荷载—位移曲线对比，曲线都为陡变型曲线，采用切线相交法从荷载—位移曲线中计算得到各工况下模型试验和有限元计算所得极限承载力值，对比结果见表4。

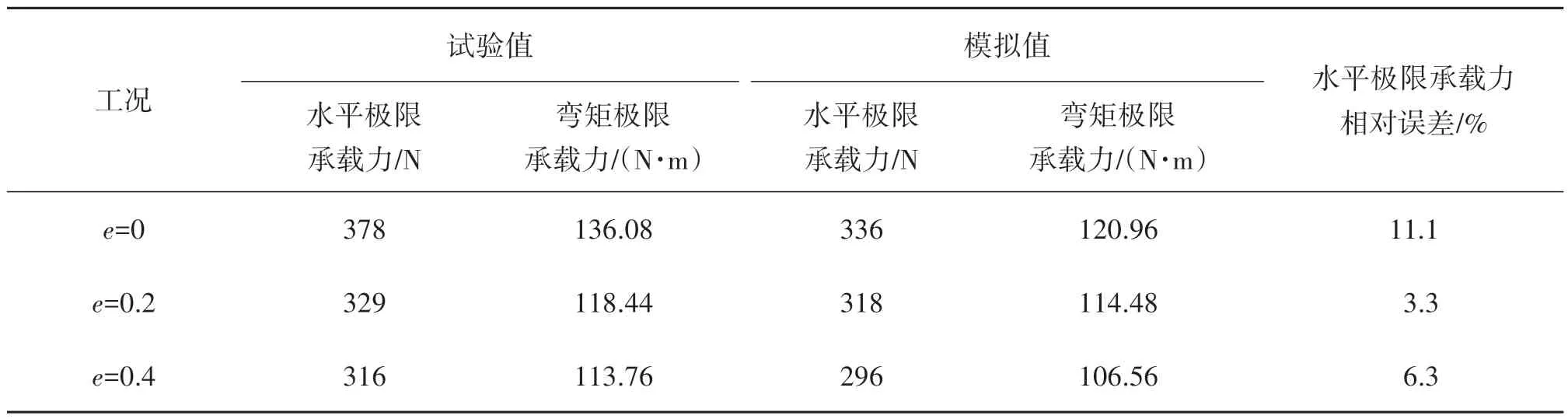
表4 极限承载力试验值和模拟值对比Tab.4 The comparison of ultimate bearing capacity between test and FEM

图9 有限元与试验结果对比Fig.9 The comparison between FEM and experiment result

当荷载—位移曲线拐点不明显，荷载超过某个值后，曲线的斜率会随荷载的增大而逐渐的增大，取曲线刚开始以及最终位置的两条切线交点对应的荷载值作为极限承载力大小，如图10中A点所示。三筒基础在无冲刷的工况下试验所得极限承载力为378 N，有限元计算所得结果为336 N，误差为11.1%，原因可能是该工况试验每级加载时间间隔较长。冲刷率为0.2和0.4的工况误差分别为3.3%和6.3%，误差较小，验证了本文研究三筒基础在冲刷条件下的承载力有限元模型的合理性和结果的可靠性。

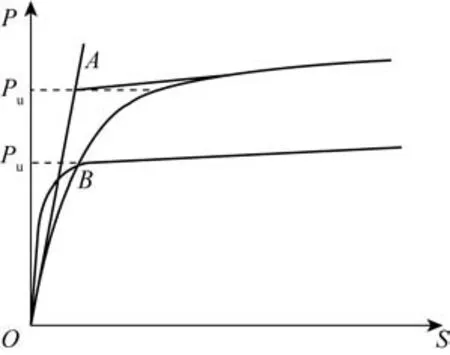
图10 典型荷载—位移曲线Fig.10 Typical load-displacement curves

2.2 水平承载力的影响

本节主要研究不同冲刷率e对不同相对筒间距S/D的三筒基础的水平极限承载力的影响，通过有限元模拟的荷载加载法，分别对S/D=2.5、3.0、3.5，冲刷率e=0、0.2、0.4、0.6共12组工况进行三筒基础水平加载模拟，通过得到的水平荷载—位移曲线，确定水平极限承载力和水平承载力效率系数，并分析冲刷率对水平承载力效率系数的影响，根据分析结果提出冲刷条件下三筒基础水平承载力效率系数计算方法。根据模拟所得不同相对筒间距下三筒基础的水平荷载—位移曲线，使用切线相交法确定水平极限承载力Hult。

由图11 可以看出：相对筒间距S/D=2.5、3.0、3.5 的三筒基础，水平极限承载力随冲刷率e的增大而减小，且下降速率随冲刷率增大而增大。这是因为三筒基础的水平承载力主要由筒内土体和筒外被动区土体提供［20］，加载过程中会在筒前形成楔形破坏区，随着冲刷率的提高，筒前侧提供抗力的土体体积减少，从而三筒基础水平承载力减小；因模拟冲刷条件时考虑了冲刷坑的形态而非简单挖去一定深度的土层，故随着冲刷率的提高，筒前侧楔形破坏区土体体积的减少幅度也提高，因此水平承载力的下降速率随冲刷率的增大而增大。纵向对比不同相对筒间距的三筒基础的水平极限承载力变化曲线可知：相对筒间距S/D越小，水平极限承载力越小，且水平极限承载力随冲刷率提高而下降的速率越快。这说明在水平荷载下，相对筒间距越小的三筒基础抵抗冲刷削弱水平承载力的能力越差。

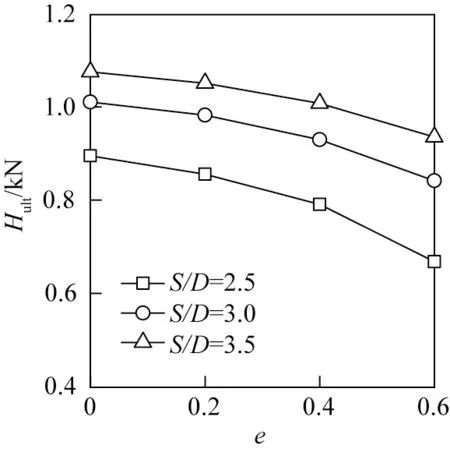
图11 水平极限承载力和冲刷率的关系曲线Fig.11 The relationship between horizontal bearing capacity and scour rate

对各模拟工况所得承载力进行无量纲化、归一化处理。荷载、位移标记方法如表5 所示。表中：EcH、EcM分别为水平和弯矩承载力效率系数；Hult，S、Mult，S表示无冲刷时单筒基础水平和弯矩极限承载力；Hult，T和Mult，T分别表示各工况对应冲刷率的三筒基础水平和弯矩极限承载力；单筒基础与三筒基础具有相同直径D、长径比L/D。

表5 荷载和位移标记方法Tab.5 Load and displacement marking method

引入冲刷修正系数dhe，以无冲刷工况的水平极限承载力为标准，对各工况的水平极限承载力进行归一化，见式（2）。

其中，EcH（e=0）为无冲刷工况的水平承载力效率系数。

根据图12 中冲刷修正系数dhe随冲刷率e的变化趋势，选用二次函数为拟合函数，依次代入4 组冲刷率e和冲刷修正系数dhe，使用最小二乘法经过多次迭代计算，得到冲刷修正系数dhe和冲刷率e的二次函数关系如式（3）所示，从图12中可以看出曲线拟合度较好。

图12 冲刷修正系数dhe随冲刷率e变化曲线Fig.12 The relationship between dhe and e

式中：α=-0.180 6exp（-0.364 8S/D）；β=4.139 9exp（-0.792 4S/D）；0≤e≤0.6；2.5≤S/D≤3.5。

2.3 弯矩承载力

图13 为不同相对筒间距的三筒基础的弯矩极限承载力随冲刷率的变化曲线，可以看出：相对筒间距S/D=2.5、3.0、3.5 的三筒基础，弯矩极限承载力随冲刷率e的增大而减小，且下降速率随冲刷率增大而增大，这是因为随着冲刷率增大，三筒基础入土深度减小，弯矩荷载作用下受拉筒周围的土体提供抵抗上拔的能力减小。

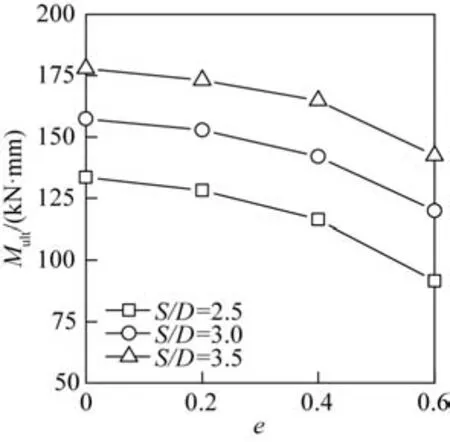
图13 弯矩极限承载力和冲刷率的关系曲线Fig.13 The relationship between bending moment capacity and scour rate

引入冲刷修正系数dme，以无冲刷工况的三筒基础弯矩极限承载力为标准，对各工况的弯矩极限承载力进行归一化，见式（4）。

其中，EcM（e=0）为未冲刷工况的弯矩承载力效率系数。

将修正系数dme与冲刷率e、相对筒间距S/D的曲线关系进行拟合，经过多次迭代计算，得到冲刷修正系数dme和冲刷率e的二次函数关系如式（5）所示，图14中可以看出曲线拟合度较好。

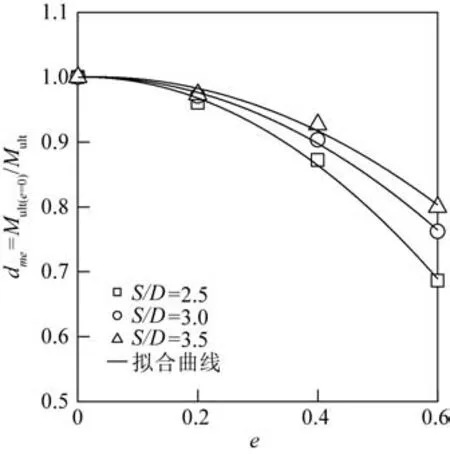
图14 冲刷修正系数dme随冲刷率e变化曲线Fig.14 The relationship between dme and e

式中：δ=-0.017 8S/D-0.030 32；ζ=-0.287 3S/D-1.589 1；0≤e≤0.6；2.5≤S/D≤3.5。

综上计算分析，对比水平荷载和弯矩荷载下冲刷修正系数dhe和dme，可以发现：冲刷修正系数dhe和dme与冲刷率e都存在二次函数关系，dhe和dme随e增大而减小，且减小速率随e增大而增大，说明冲刷深度越大，冲刷对三筒基础的水平抗弯承载力削弱越强。当冲刷率e=0.6时，S/D为2.5、3.0、3.5的三筒基础水平承载力的冲刷修正系数dhe分别为0.746、0.833、0.871，而弯矩承载力的冲刷修正系数dme分别为0.686、0.762、0.800，对比可以发现不同相对筒间距的三筒基础水平承载力的冲刷修正系数dhe大于弯矩承载力的冲刷修正系数dme，说明冲刷对抗弯承载力的影响大于对水平承载力的影响。

2.4 冲刷对M-H包络线影响

吸力式多筒基础在工作中主要承受自重带来的竖向荷载和波浪、海流所引起的水平与弯矩荷载的复合加载。文献［15］表明，当筒型基础所受竖向荷载小于竖向极限承载力的0.4倍时，竖向荷载对其承载力包络图的影响不大，因此本节将主要研究吸力式三筒基础在M-H应力空间内的承载特性受冲刷作用的影响。

采用固定荷载比方法，对相对筒间距S/D分别为2.5、3.0、3.5的三筒基础进行水平和弯矩复合加载模拟，并将各模拟工况所得极限承载力进行无量纲化、归一化处理，无量纲化处理可以更清晰地看出包络线的位置变化，归一化处理可以更容易对比出包络线的形状变化。不同相对筒间距S/D和不同冲刷率e下的M-H无量纲与归一化破坏包络线如图15和图16所示。

图15 M-H无量纲破坏包络线Fig.15 Non-dimensional M-H envelope curves

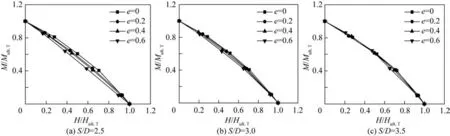
图16 M-H归一化破坏包络线Fig.16 Normalized M-H envelope curves

通过图15可以看出冲刷率对无量纲包络线的影响较大。随着冲刷率的提高，三筒基础的水平和弯矩极限承载力均减小，导致M-H破坏包络线向内移动，且移动范围随冲刷率的提高而不断变大。说明随着周围土体缺失深度和范围的增大，三筒基础的水平和弯矩承载力不断降低，且随着冲刷率的上升，水平和弯矩承载力降低幅度增大。

通过图16可以看出，不同冲刷率下，三筒基础的归一化破坏包络线在第一象限内重合率较高，该现象与单筒基础一致［10］。对比各工况下三筒基础的M-H归一化破坏包络线，发现各包络线形状相似：随着水平力的增加，极限弯矩值明显降低；随着相对筒间距S/D增大，破坏包络线呈上凸的趋势，三筒基础的水平和弯矩极限承载能力随着相对筒间距的增大而小幅提高，这是因为相对筒间距增大，三筒基础的弯矩力臂增加，结构整体稳定性更强。

对比文献［25-26］中筒型基础的M-H破坏包络线公式的研究（图17）可见，本研究模拟所得包络线与Hung和Kim［26］的结果比较接近。故这里在Hung和Kim的研究基础上，引入相对筒间距S/D和冲刷率e，采用式（6）对M-H破坏包络线进行拟合。

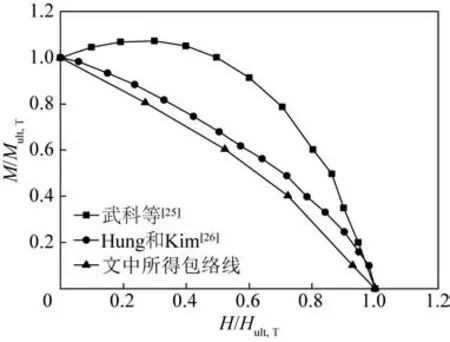
图17 归一化破坏包络线对比Fig.17 The comparison of normalized envelope curves

经过多次迭代计算，得到各工况下的修正系数η值见图18。

图18 修正系数与冲刷率对应关系Fig.18 The relationship between η and e

根据式（6）的函数特性：修正系数η趋近于0 时，第一象限内形状接近1/4 圆弧；η趋近于2 时，第一象限内形状接近斜率为-1、截距为1的直线。纵向对比图18中相同e、不同S/D的修正系数η可发现：相同冲刷条件下，三筒基础的相对筒间距越大，η越小，M-H破坏包络线形状越外凸，即水平、抗弯承载性能越好。对比不同S/D下，修正系数η随冲刷率e变化曲线可知：随着冲刷率的上升，S/D=2.5时η的变化幅度最大，S/D=3.5时η的变化幅度最小。说明相对筒间距越大，水平、抗弯承载力受冲刷率的影响越小，抗冲刷能力越强。

将修正系数η与冲刷率e、相对筒间距S/D进行拟合计算可得三筒基础M-H归一化破坏包络线计算公式：

式中：γ=-0.083 5S/D+1.437 3；λ=-0.553 9S/D+2.000 9；μ=10.740S/D-3.098；0≤e≤0.6；2.5≤S/D≤3.5。

图19为通过拟合计算所得破坏包络线与试验数据的对比，可以看出不同冲刷工况的极限承载力试验数据均在破坏包络线附近，验证了包络线计算公式的合理性。

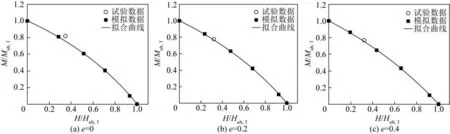
图19 包络线计算公式与试验数据对比Fig.19 The comparison between calculation formula and test result

3 结 语

结合模型试验和数值模拟对吸力式三筒基础在水平、弯矩作用下的破坏模式和极限承载力受冲刷的影响进行研究。得出以下结论：

1）冲刷条件下三筒基础受水平和弯矩作用直至破坏的过程，经历弹性变形阶段—塑性变形阶段—失稳破坏阶段，三筒基础提供的水平弯矩抗力主要来自筒前土体被动土压力和筒壁内外侧与土体的摩擦。

2）三筒基础的水平极限承载力随冲刷率e的增大而下降，且下降速率随冲刷率增大而增大。考虑文献中最优筒间距取值，当相对筒间距的范围为2.5～3.5 时，相同长径比的三筒基础水平极限承载力随相对筒间距的减小而降低，但水平承载力受冲刷影响而下降的速率随相对筒间距的减小而提高。

3）冲刷率e对M-H无量纲破坏包络线的影响较大：随着冲刷率的提高，三筒基础的水平和弯矩极限承载力均降低，导致M-H破坏包络线向内移动，且移动范围随冲刷率的提高而不断变大。说明随着周围土体缺失深度和范围的增大，三筒基础的水平和弯矩承载力不断降低，且随着冲刷率的上升，水平和弯矩承载力降低幅度增大。不同冲刷率下，三筒基础的M-H归一化破坏包络线在第一象限内形状相似，随着水平力的增加，极限弯矩值明显降低；随着相对筒间距S/D增大，归一化破坏包络线呈上凸的趋势，这是因为三筒基础的弯矩力臂随着相对筒间距的增大而增大，结构整体稳定性更强。