岛礁地形上斜坡堤前破碎波流场数值模拟研究
黄晶鑫,杨 氾,潘军宁,王登婷,刘清君
(南京水利科学研究院 河流海岸研究所,江苏 南京 210024)
岛礁是一种岸坡非常陡峭的海岸地形,波浪从深水传播至岛礁时,水深发生急剧变化,使波浪发生浅水变形并破碎,随后在平坦的礁坪上继续向前传播。波浪破碎过程中产生的波动流场,对岛礁底部冲淤变化、岛礁周围生物环境及防波堤护底和护面结构等产生很大影响。因此研究岛礁地形上波浪破碎过程中的波动流速分布具有重要意义。
国内外学者采用现场观测、物理模型试验及数值模拟等手段对波浪在岛礁上的传播变形进行了大量研究。何栋彬等[1]采用非线性Boussinesq 型方程波浪模型,进行了规则波和随机波在礁坪上传播的数值模拟。谭安平等[2]应用FLOW-3D 数值软件开展了珊瑚礁地形下防波堤波浪爬高特性研究。诸裕良等[3]采用非线性Boussinesq 型方程数值软件FUNWAVE-TVD 模拟了礁坪上波浪破碎过程与增水特征。刘林平等[4]基于FUNWAVE-TVD 对孤立波在理想化三维岛礁地形上的传播及爬坡开展了现场尺度的平面二维数值模拟,结果表明:珊瑚礁的存在总体上可有效降低岛屿四周孤立波的最大爬坡高度;入射波高、礁坪水深、礁坪宽度、珊瑚礁糙率是影响珊瑚岛礁四周孤立波爬坡分布的主要因素。
除上述基于欧拉法的数值模型外,拉格朗日型无网格粒子法——光滑粒子流体动力学法(smoothed particle hydrodynamics,简称SPH)也常被用于波浪破碎的模拟。该方法于1977 年分别由Lucy[5],Gingold 和Monaghan[6]独立提出,最初应用于解决天体物理学中的星系碰撞、流星冲击等问题,之后发展至自由表面流[7]、多相流[8]、流固耦合[9]等问题的数值求解当中。温鸿杰[10]基于SPH方法建立了一个能够精确描述OWC式波能转换装置附近水动力特性的湍流模型,并改进了控制方程中的耗散项,克服了在进行长时间的数值模拟时自由液面处流体粒子向上漂移的现象。任冰等[11]建立了基于SPH 法的二维数值波浪水槽,模拟了规则波对透空式结构物的冲击作用,并通过黎曼解和CSPM 相结合的方法对连续方程和动量方程进行了修正。温鸿杰等[12]基于SPH 模型采用周期性边界较好地模拟了规则波在深海岛礁上的传播变形过程以及礁坪上波浪增水空间分布。Dalrymple和Rogers[13]模拟了波浪越浪和浅滩破碎等问题并验证了SPH方法的适用性。Altomare 等[14]模拟了采用复杂护面块体的防波堤在波浪作用下的波浪爬高,验证了SPH 方法在模拟该类问题中的可行性。Khayyer 等[15]在不可压SPH 法的基础上进行了修正,改善了波浪破碎的模拟效果。Lowe等[16]研究了岛礁上不规则破碎波的流场。但目前尚缺乏对岛礁上破碎波作用下斜坡堤前波动流场的相关研究。
鉴于波动流场尤其是近底流速对堤前冲刷预测和护底设计的重要性,基于SPH 模型建立数值波浪水槽,开展规则波作用下斜坡堤对岛礁地形上波浪传播变形和破碎波流场影响的数值模拟研究。首先模拟无防波堤时波浪在礁坪上的破碎过程,将礁缘前后不同位置处波动流速最大值垂线分布与波浪水槽物理模型试验测量结果进行比较,以验证SPH 模型的准确性和适用性;之后在数值水槽中添加斜坡堤,模拟分析建堤后礁坪上波动流场及波高的变化特征。
1 数值模拟方法
数值模拟采用基于SPH 方法的开源程序DualSPHysics[17-18],该程序应用了CUDA 技术以支持GPU 运算,具有较高的性能和较好的适用性。
1.1 控制方程及其离散格式
弱可压SPH法中的控制方程为N-S方程,连续性方程和动量方程为:
式中:ρ为流体密度;t为时间;u为速度矢量;P为应力张量;g为重力加速度;Γ为耗散项。
在SPH 法中,一个粒子在某一时间点的物理量通过使用核函数被离散化为该粒子周围支持域内临近粒子的物理量的求和,物理量的梯度采用核函数的梯度来表达。
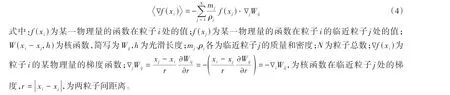
核函数需要满足一定条件[19],主要包括:1)紧支性,在支持域外时,函数值恒为0;2)局域性,在支持域内时,函数值恒大于等于0;3)衰减性,粒子距离增大时,函数单调递减。采用的核函数为Wendland[20]提出的五阶样条函数:
式中:αD为归一化常数,在二维问题中αD= 3 (2πh2),在三维问题中αD= 15 (16πh2);q=r/h,无量纲量,为初始粒子间距与光滑长度的比值。
利用式(3)和式(4)将式(1)、式(2)中的物理量离散化后即可得到粒子离散形式的控制方程。在弱可压SPH法中,粒子的质量为恒定值,计算过程中粒子密度发生变化[14]。
δ-SPH法在连续性方程中引入了人工黏性项,提高了计算的稳定性。采用了δ-SPH法的连续性方程为:

式中:α为人工黏度系数,研究[14,18]表明α= 0.01 为保证计算稳定性及避免非物理性振荡的最小值;-cij=0.5(ci+cj)为平均声速;μij=huij·rij(rij2+η2)为黏性系数,其中η2= 0.01h2;uij=ui-uj、rij=ri-rj分别为粒子i与粒子j处的速度矢量差和位置矢量差。
在研究礁坪上波浪破碎问题时,人工黏性理论中采用的人工黏度系数会造成过大的数值耗散[21],文中计算根据边界层黏性理论(laminar viscosity)[22]及亚粒子尺度湍流模型(sub-particle scale turbulence)[13]对其进行了优化。采用了边界层黏性理论和亚粒子尺度法后的动量方程离散形式:
式中:ν0为边界层中的运动黏度;τi、τj分别为i、j处的应力张量。
当采用弱可压假定时,粒子处压力依据粒子处密度通过状态方程计算得出,数值计算中采用的时间步长由流体中的声速计算确定[23]。为了使计算时间步长保持在合理范围内,弱可压假定中调整了流体的可压缩性,从而可以采用较低的流体声速。为了保证计算稳定性,密度变化需限制在1%以内,因此声速需要大于10倍的最大流体速度。状态方程为[24]:

式中:ri为粒子i的位移量。
1.2 边界条件
水槽中的固边界采用动态边界条件法(dynamic boundary condition,简称DBC)[25]。该方法将结构边界离散为粒子后,边界粒子视为同样满足流体粒子的控制方程,并参与流体粒子控制方程的计算,但边界粒子的位置不发生改变。
造波方法采用推板式造波板法,基于二阶规则波造波理论,造波板位移量为:
式中:e(t)为造波板位移量;S0=H m1为造波板冲程;ω= 2πT为波浪圆频率;ϕ为初始相位;H为波高;k= 2πL为波数;d为静水水深。
在使用推板式造波板法的过程中应用主动消波法可以消除二次反射波的影响。主动消波法(active wave absorption system,简称AWAS)[26]通过检测造波板前的实际波面升高与理论值的差异来调整造波板的运动,从而对波面进行修正。造波板运动修正方程为:
式中:ηR(t)为理论波面升高和实际波面升高的差值;ηI(t)为理论波面升高;ηSPH(t)为SPH 计算所得的造波板前的实际波面升高;UR(t)为造波板速度的修正量。
水槽末端消波采用阻尼消波方式。阻尼消波通过修改粒子行进过程中的速度实现消波:
式中:v为修改后的粒子速度;v0为修改前的粒子速度;Δt为时间步长;β为可调节的速度削减参数;x为当前粒子位置;x0、x1分别为消波区的起始位置和结束位置。
1.3 时间积分
时间积分方法采用对偶位置Verlet 法(symplectic position verlet scheme),该方法具有二阶精度,并且在采用了人工黏性项时仍具有时间可逆性和对称性。当采用显式时间积分法时,时间步长取决于库朗数(courant-friedrichs-lewy,简称CFL)、压力项和黏性扩散项。
1.4 模型设置
采用上述SPH 方法建立岛礁地形上破碎波作用的二维数值水槽模型,图1 所示为未设防波堤的数值水槽布置示意图。水槽整体尺寸为50 m×1.5 m(长×高);礁前静水水深0.6 m,礁坪静水水深0.1 m;坡前水平段长5.0 m,斜坡坡度为1∶1,长0.5 m,高0.5 m。水槽最左侧为推波板,产生向右行进的规则波。试验中波高H为0.085 m,周期T为1 s。水槽末端为人工阻尼消波区,以消除水槽右边界反射波的影响。

图1 未设防波堤的数值水槽布置示意Fig.1 Schematic diagram of a numerical wave flume in the absence of a slope breakwater
1.5 模型验证
为验证SPH 模型在模拟岛礁地形上的波浪传播变形方面的准确性,在波浪水槽中进行了物理模型试验,开展对比研究。图2 所示为物理模型试验水槽布置示意图。水槽尺寸为60.0 m×1.8 m×1.6 m(长×宽×高)。水槽一端配有推板式造波机,在两端均配有消浪缓坡及消浪装置。礁缘距造波机26 m,礁坪高0.5 m,试验水深及波要素与数值模型相同。水槽中选取3条流速测线,分别位于岛礁斜坡中间处、礁缘前、礁坪上,1#、2#和3#测线距礁缘距离分别为-0.25,-0.10,0.80 m,各测点垂向高度见表1。另在礁缘前0.50 m、礁缘处及礁缘后0.50 m 处分别设置A、B、C 三个波高仪。流速测量采用Vectrino 小威龙声学多普勒点式流速仪(ADV),波高测量采用LG1型电容式波高仪,采用DS30型64通道浪高水位仪系统进行数据采集。

表1 模型验证测点位置Tab.1 The location of measurement points for model validation 单位:m

图2 物理模型试验水槽布置示意Fig.2 Schematic diagram of a physical wave flume
将数值模拟得出的各测点正向及反向水平波动流速最大值的垂线分布与物理模型试验结果进行对比(见图3),可见数值模拟的波动流速与试验测量结果总体符合较好,3#测线处数模计算的流速幅值略小。由于波浪破碎导致能量损耗,礁坪上3#测线处波动流速显著小于礁缘前1#和2#测线处波动流速。图4给出了1#、2#和3#测线近底水平波动流速变化过程验证情况,图5 为3 个波高测点处的波面过程对比图,从图中可以看出,SPH 模型的近底流速和波面过程模拟结果与物理模型试验结果呈现良好的一致性。数值模拟与物理模型试验在A波高仪处的波高分别为8.72、8.89 cm;在B波高仪处的波高分别为6.12、6.31 cm;在C波高仪处的波高分别为4.65、4.92 cm。

图3 数值模拟结果与物理模型试验结果中各点水平波动流速正、反向幅值对比Fig.3 Comparison of the forward and reverse amplitudes of the horizontal fluctuation velocity of the numerical simulation results and the physical model test results

图4 不同测点处近底水平波动流速变化过程对比Fig.4 Comparison of near-bottom horizontal fluctuation velocity variation at various measuring points

图5 不同测点处波面升高过程对比Fig.5 Comparison of wave surface elevation processes at various measuring points
由图3~5 可见:在礁坪前,A 点处波面过程已表现出波峰前波面上升速度大于波谷前波面下降速度、波峰陡峭、波谷平缓及波谷历时大于波峰历时等非线性前倾波特征,但1#和2#测线近底水平波动流速仍为线性正弦波形态,正、反向水平波动流速最大值垂线分布均表现为自上而下逐渐减小的趋势。在礁坪上,由于波浪破碎,波面和近底水平波动流速过程的非线性特征更为显著:B 和C 点处波峰高度显著大于波谷深度,波峰历时显著小于波谷历时;3#测线近底正向流速最大值小于反向流速最大值,正向流速历时也小于反向流速历时,正向水平波动流速最大值由上向下逐渐减小,反向水平波动流速最大值则逐渐增大。
2 礁坪上斜坡堤对波动流场的影响
为研究斜坡堤对礁坪上波动流场的影响,分别采用SPH 数值水槽进行了有、无斜坡堤情况下的数模计算。计算中采用规则波,波浪要素、礁前水深等参数均与前文相同。图6所示为设有防波堤的数值水槽布置示意图。斜坡式防波堤设置在礁缘后0.8 m处,其坡度为1∶2,长6 m,高3 m,其余尺寸如图6所示。

图6 设有防波堤的数值水槽布置示意Fig.6 Schematic diagram of a numerical wave flume with a slope breakwater
图7为有堤和无堤情况下不同时刻岛礁波动流场对比图。由图7可见:有斜坡堤时,波浪在防波堤前发生反射,波动水体在堤坡上呈现周期性爬高、回落现象,波浪反射及爬高后回落水流对防波堤前流场造成显著影响。t=0时,前波在破碎后波峰传播至堤脚处,后波波峰在礁缘前发生剧烈变形,前缘变得陡峭,有堤与无堤时礁缘前至礁坪中段的波浪形态基本相同,有堤时出现波浪沿堤坡上爬现象。t=0.25T时,有堤时前波在堤坡上进一步爬高,后波波峰在礁坪上发生卷破,破碎点波高大于无堤时。t=0.50T时,后波在破碎后形成破后波,有堤时前波爬高水体回落,后波受反射波影响破碎紊动更为强烈,在波面下形成漩涡。当t=0.75T时,后波波峰传播至堤前,有堤时波峰较无堤时显著抬高,并再次发生卷破。总体上看,防波堤对礁坪上的波动流场形态产生很大影响,使波浪破碎更加猛烈,产生漩涡和紊动等复杂流体运动现象。

图7 有堤和无堤时的岛礁部分流场示意Fig.7 Schematic diagram of part of the reef flow field with and without slope breakwater
为具体研究斜坡堤对岛礁流场的影响,对有、无堤时礁坪上不同位置处最大水平波动流速进行对比分析。从礁缘(图6中5.5 m 处)至堤脚每隔0.1 m 设置一条垂线,每条垂线布置6个计算点,计算点垂向高度分别为0.560、0.540、0.530、0.520、0.510、0.505 m。图8 为有、无堤时各点水平波动流速正、反向幅值对比图,从图中可见流速变化随水平位置呈现显著波动:有堤时,距礁缘0.1~0.3 m 及0.7 m 处正向流速较无堤时减小,其他位置正向流速增大,其中距礁缘0.2 m 处最大减小50%左右,距礁缘0.5 m 处约增大100%;有堤时反向流速除距礁缘0.1~0.2 m 及0.6~0.7 m 处略有增大或与无堤时接近外,其余点均显著增大,其中距礁缘0.4 m处最大增大约90%。

图8 有堤和无堤时各点水平波动流速正、反向幅值对比Fig.8 Comparison of forward and reverse amplitudes of horizontal fluctuation velocity with and without slope breakwater
图9 为有堤和无堤时波高及近底水平波动流速幅值沿程分布图。无堤时,由于波浪破碎后水体强烈紊动导致能量损耗,波高和波动流速均从礁缘处向礁缘后方逐渐减小。有堤时,由于堤前波浪反射的影响,入射波和反射波叠加导致波高和近底流速幅值均呈现沿程起伏波动现象:波高在距堤脚0.649 倍波长和0.108倍波长附近出现峰值,流速减小;波高在距堤脚0.455 倍波长附近出现谷值,流速则增大。总体上符合波浪部分反射时堤前波高和流速变化规律,但在堤前半倍波长范围内(5.85~6.30 m区间段)有堤时反向近底流速峰值增幅较大,显著大于波高峰值增幅,且正向和反向流速峰值出现位置略有不同。

图9 有堤和无堤时波高及近底水平波动流速幅值沿程分布过程Fig.9 Spatial distribution of wave height and near-bottom horizontal fluctuation velocity amplitude in the presence and absence of a slope breakwater
为确定斜坡堤前护面块体重量,《防波堤与护岸设计规范》(JTS 154—2018)[27]推荐按下式计算堤前最大波浪底流速:
式中:Vmax为斜坡堤前最大波浪底流速;H为设计波高;L为计算波长;d为堤前水深。在堤前半倍波长范围内,由式(17)和无堤时区间最大波高计算的最大底流速为0.254 m/s,而数模计算的区间最大近底流速较之增大约70%;在礁坪上距斜坡堤脚0.87~0.76 倍波长、0.63~0.28 倍波长及接近堤脚处的流速大于规范值。因此在岛礁地形上需注意加强堤前护底结构。
3 结 语
基于SPH 模型建立波浪数值水槽,对岛礁地形上的波浪传播变形进行了数值模拟,并与物理模型试验数据进行对比,验证了SPH 方法在模拟岛礁地形上波浪传播变形方面的可行性。比较分析了有、无斜坡堤情况下礁坪上的波浪破碎过程、流场形态及流速分布。
在无堤情况下,波浪在破碎前水平波动流速最大值自上而下逐渐减小,在礁坪上破碎后呈现出非线性特征,正向水平波动流速最大值自上而下逐渐减小,反向水平波动流速最大值自上而下逐渐增大。
有斜坡堤后,波浪破碎更加猛烈,并产生漩涡和紊动等复杂流体运动现象;波浪破碎点前移,同时波浪破碎后的紊动区前移,并且紊动更加剧烈;受反射波影响,礁坪上波高呈现为先增大、再减小、再增大,最后在防波堤堤脚处减小,近底流速变化趋势则与之相反。在堤前半倍波长范围内,有堤时反向近底流速峰值增幅较大,岛礁上斜坡堤护底结构设计应关注这一现象。

