台阶式沉井等效墩宽计算方法探究
闻云呈,朱大伟,王晓俊,成泽霖,3,张帆一,夏明嫣
(1.南京水利科学研究院,江苏 南京 210024;2.江苏省水利勘测设计研究院有限公司,江苏 扬州225009;3.海岸灾害及防护教育部重点实验室(河海大学),江苏 南京 210098)
研究桥墩局部冲刷问题时,桥墩宽度D是最重要的参数之一。常规沉井因施工挡土的需要,沉井顶部与底部截面尺寸总是设计成相同大小,研究局部冲刷时其计算墩宽取沉井迎水面宽度D即可。然而从结构构造考虑,沉井顶面尺寸仅需满足塔柱布置以及上部结构传力的需要[1]。对于超大型沉井,其实际需要的顶部尺寸往往比沉井底部平面尺寸小的多,这为沉井台阶的设置提供了条件。为节约建设成本,便于施工,同时减小局部冲刷带来的影响,在建主跨1.176 km 的常泰长江大桥主墩已首次应用了台阶式沉井这一设计,如图1 所示,沉井顶部宽度D1=39.8 m,底部宽度D2=57.8 m,台阶平台埋深位于床面以下0.6 倍水深处[2]。此外,拟建主跨度1.78 km 的盐泰锡常宜铁路长江大桥主桥墩也已采用了该结构设计(D1=39.8 m,D2=63.0 m)。对于台阶式沉井结构,研究局部冲刷时计算墩宽的选取则需额外考虑桥墩截面的非均匀性。

图1 台阶式沉井基础现场照片及示意Fig.1 The main pier of Changzhou-Taizhou Yangtze River Bridge (under construction) and its schematic diagram
随着沉井截面尺寸的不断增大,基础周围的河床冲刷深度也不断增大。以泰州长江大桥主塔沉井(D=44.1 m)为例,2020年大洪水后,监测资料表明最大局部冲刷已发展到30.8 m,短期大幅的局部冲刷给桥梁的安全运维以及由此对周边带来的影响不容忽视,因此有必要对局部冲刷深度进行准确度更高的预测。在桥墩尺度上,最大局部冲刷深度由墩宽、水深和床面可蚀性共同决定。其中,影响流场结构的墩宽和水深最为重要[3]。因此非均匀桥墩墩宽的计算对局部冲刷的准确预测至关重要。
在相关研究中,通常使用等效墩宽对非均匀桥墩的非均匀性进行量化描述。等效墩宽De是指在相同的水流和泥沙条件下,与非均匀桥墩产生相同局部冲刷深度的圆柱型桥墩的直径。一般等效墩宽被认为是结构自身参数的函数,与其他要素无关。台阶式沉井这类桥墩的特点在于随着沉井埋置深度的改变,其冲刷特性有所变化,等效墩宽也会改变。因此部分经验系数方法并不适用,如Sheppard等[4]使用桥墩投影宽度乘以固定系数确定桥墩与水流正交时的等效墩宽。当前国内外大多相关研究均使用加权平均公式计算该类桥墩的等效墩宽,量化非均匀桥墩的非均匀性,然而这些方法存在一定差异。这里针对台阶式沉井结构,对各类等效墩宽计算方法进行了讨论,并结合试验数据对不同方法计算结果进行对比分析。
1 台阶式沉井计算方法理论分析
在《公路工程水文勘测设计规范》(JTG C30—2015)[5]及陆浩和高冬光编著的《桥梁水力学》[6]中,给出的台阶式沉井类非均匀桥墩的等效墩宽计算方法如下:
式中:h1与h2分别代表桥墩上下两部分结构在水中的高度,如图2(a)所示;D1和D2分别表示桥墩上下两部分迎水面宽度;h为水深。经分析该公式也可通过阻水效应守恒条件推导得到。基于流量守恒原理,根据水下构筑物结构尺寸并结合流速分布,可推导得到桥墩的平均阻水宽度如下[7]:
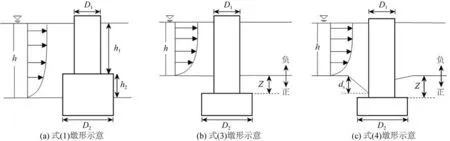
图2 不同等效墩宽计算公式墩形示意Fig.2 The schematic diagrams of piers for different equivalent pier width calculation methods
其中,U(z)表示高程z处流速,D(i)表示对应高程处桥墩迎流面宽度。考虑到天然河道中流速垂向分布较为均匀[8],忽略近底边界层中的流速梯度差异,对于上下部分迎水面宽度不同的台阶式沉井结构,式(2)即可简化为式(1)的形式。已有研究表明,沉井下部埋置于床面以下一定深度能够有效减小局部冲刷深度[9-10]。然而,式(1)并未考虑沉井下部结构埋置于床面以下,即h2为负值的情况,如图2(b)所示。因此对于台阶式沉井,等效墩宽公式可依据上述思路拓展为以下形式:
其中,Z表示沉井下部结构埋置深度,台阶低于床面时为正值,反之为负值。当Z<0时,式(3)与式(1)等价。
根据上述分析可知,规范中台阶式沉井的计算墩宽公式仅考虑了定床条件下的平均阻水宽度,而并未考虑水深会随着局部冲刷坑发展而变化的实际情况。等效墩宽最终需要描述的是冲刷平衡时与目标桥墩冲刷深度相同的等效圆柱型桥墩宽度,因此有必要考虑冲刷坑发展对等效墩宽的影响。通常局部冲刷深度的数量级与墩宽相当,这一深度相对于桥墩尺寸不可忽略。因此需要引入局部冲刷深度ds以描述局部冲刷达到平衡后水深的改变对等效墩宽的影响,如图2(c)所示。考虑局部冲刷深度的影响后,台阶式沉井的等效墩宽计算公式可以改写为以下形式:
由于局部冲刷深度ds事先无法预知,因此式(4)难以直接应用。针对这一问题,Melville 和Raudkivi[11]使用了近似处理方法,基于非均匀圆柱型桥墩局部冲刷试验数据,提出了一种等效墩宽加权平均计算公式,与式(3)类似,该式中等效墩宽De仅与水深h、墩宽D及埋置深度Z相关:
公式适用范围为Z≤D2并且-Z≤h。观察式(4)与式(5)可以发现二者差异仅有一处,即式(5)中使用D2将式(4)中的局部冲刷深度ds进行了替换,因此该公式本质上也是基于动床条件下的流量守恒原理得到的加权平均公式。由此可见,上述国内外对于等效墩宽的研究实际上是计算不同条件下的桥墩平均阻水宽度。
除上述根据流量守恒原理推导得到的公式外,一些学者针对由桥墩、承台及群桩组成的复杂桥墩(国外文献中一般表述为complex pier)也提出了适用范围更广的等效墩宽计算公式[12-13]。将群桩等效墩宽等价于沉井基础下部直径D2后,这些公式也可应用于台阶式沉井等效墩宽的计算。这些公式依赖大量不同类型桥墩的局部冲刷试验数据得到,往往过于复杂和经验化,因此这里对此不具体展开讨论。
2 台阶式沉井等效墩宽计算方法对比分析
2.1 台阶式沉井局部冲刷试验
针对3类沉井结构开展了局部冲刷试验,其中1类沉井为无台阶大型沉井,另外2类沉井为台阶式沉井,试验用桥墩模型如图3所示。3类沉井下部完全一致,即D2=20 cm,其中D1=14 cm 的台阶式沉井下文称为中型沉井,D1=10 cm 的台阶式沉井下文称为小型沉井。台阶式沉井模型下部可拆卸,安装不同高度的基础可实现不同埋置深度的局部冲刷试验要求。

图3 3类沉井模型照片(左)及上部截面参数(右)Fig.3 Photos of three caisson models (left) and parameters of upper section (right)
在试验水槽中进行冲刷试验,试验水槽尺寸为40 m×1.9 m×0.5 m(长×宽×高),配有独立的循环回水系统。试验水槽可根据不同工况需求调整流量、流速及水深。水槽上游采用变频器自动控制出水流量,在进口处设置有整流栅,对进入水槽中的水流进行消能及调整以快速达到稳定状态;下游通过推拉式尾门跟踪水位,通过控制尾门开合程度控制试验段水深。试验回水槽设置溢流口,稳定模型内外水位差,控制上游出流稳定性。
根据模型试验经验,在水槽进口处应保留5~7 倍水槽宽度的过渡段,使紊流发展充分,同时在出口处留有3~5倍槽宽的过渡段调整水流。因此本试验将水槽分为进水段、试验段及出水段,其中进水段长18 m,试验段长10 m,出水段长12 m。水槽模型进水段及出水段均为固定床面,表面为光滑水泥抹面。通过水位测量,推算水槽整体糙率约为0.012。水槽模型动床试验段平面示意如图4(a)所示;试验段中动床段长6 m,铺沙厚度为30 cm,剖面示意如图4(b)所示。

图4 试验段平面及剖面示意Fig.4 The schematic diagram of test section top view and side view
试验过程中水下流速采用小威龙ADV进行测量,在沉井内部布置一台水下摄像头以观测局部冲刷坑发展情况。研究中各试验工况水深流速条件均相同:试验用沙为中值粒径d50= 0.35 mm的均匀硅沙(泥沙非均匀系数σg= 1.3);沉井埋置深度Z变化范围为-10 ~20 cm,即对应的台阶平台位置变化范围为床面以上10 cm至床面以下20 cm。观测到的长时间局部冲刷发展过程表明,试验开始6小时后局部冲刷深度普遍达到平衡冲刷深度的80%以上。为提高试验效率,每组试验时间均设置为6 小时。具体试验参数及试验测量得到的最大局部冲刷深度ds如表1所示。表1中Uc为泥沙临界起动流速。
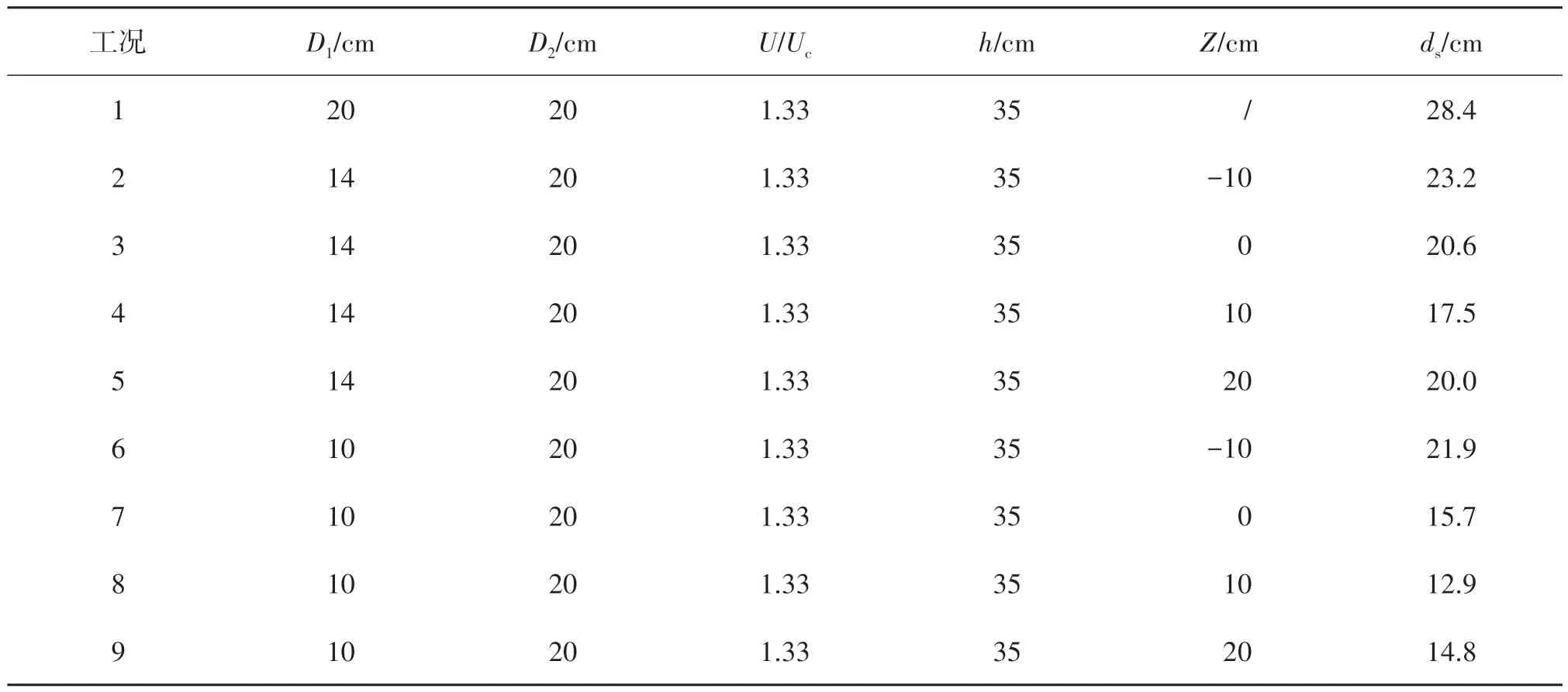
表1 台阶式沉井局部冲刷试验工况及试验结果统计Tab.1 Experimental cases setup and the equilibrium scour depth for each case
2.2 等效墩宽计算成果对比分析
将局部冲刷深度ds代入式(4)求出实际动床条件下的平均阻水宽度,并与其他等效墩宽计算公式的计算结果进行对比,如图5所示。显然,式(5)计算得到的等效墩宽与实际动床条件下平均阻水宽度最为接近;而未考虑动床水深变化的式(3)计算得到的等效墩宽则普遍偏小,随着埋置深度不断增加,偏差不断增大。当埋置深度为20 cm时(工况5和工况9),局部冲刷深度均未大于埋深值Z,沉井下部结构未因冲刷暴露在水流中,意味着此时局部冲刷未受下部结构影响,等效墩宽实际上应该为上部结构迎水面宽度D1。然而此时式(3)的计算结果已小于D1的50%,表明式(3)在沉井结构埋置深度较大时已不能准确地估算台阶式沉井实际平均阻水宽度。Coleman公式[12]与Ataie-Ashtiani等[13]公式的估算结果与实际动床条件下平均阻水宽度也存在较大的差异,这2个公式均是基于更为复杂的桥墩结构发展而来的,其对于台阶式沉井等效墩宽计算的适用性并不强。
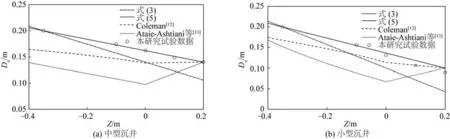
图5 不同埋置高度下等效墩宽计算Fig.5 Calculation results of the equivalent pier width for medium and small caissons at various buried heights
此外,本研究还收集整理了前人类似台阶式沉井结构(国外文献中一般表述为compound pier)的局部冲刷试验数据资料,以探究式(5)对台阶式沉井类结构的适用性。如表2 所示,收集的相关试验资料共计193组[11,14-22],包含的非均匀桥墩类型如图6所示,不同试验研究中使用的泥沙粒径覆盖了细砂至粗砂范围。

表2 台阶式沉井类桥墩局部冲刷试验资料来源及试验参数范围Tab.2 The data source and parameter range of local scour experiments for compound piers
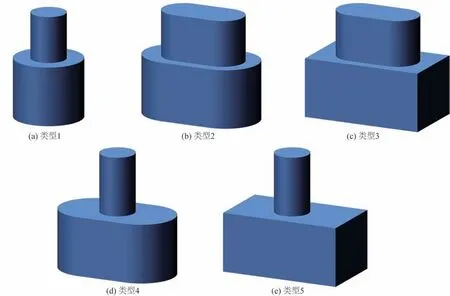
图6 数据集包含非均匀桥墩类型示意Fig.6 Schematic diagram of non-uniform pier included in the dataset
将式(5)的等效墩宽De计算结果与式(4)计算得到的实际平均阻水宽度(记为Dw)进行对比,如图7 所示。以Dw为实测值,De为预测值,统计了二者间的均方根差(RMSE)、偏差(Bias)以及平均相对误差(MRE)。统计结果显示二者较为接近,均方根差为1.01 cm,绝大多数等效墩宽计算结果误差小于15%,平均相对误差为5.46%。偏差为负值则体现了式(5)计算结果的保守性。因此可以认为式(5)能够较为准确且保守地估算台阶式沉井类结构的平均阻水宽度,能够较好地量化大多数台阶式沉井类结构的截面非均匀性。

图7 式(4)与式(5)计算结果对比Fig.7 Comparison of calculation results of Eq.4 and Eq.5
2.3 等效墩宽计算公式讨论
对于简单的圆柱型结构桥墩,一般认为最大局部冲刷深度总是小于2.5倍的桥墩直径D[23]。而对于台阶式沉井类结构,局部冲刷深度ds与沉井底部墩宽D2的比值必定小于上述值。图8 显示了基于193 组局部冲刷试验数据的冲深墩宽比ds/D2统计直方图。可以发现台阶式沉井类结构的冲深墩宽比ds/D2绝大多数情况下小于2,平均值为0.945。因此式(5)中直接使用D2代替式(4)中未知量ds存在一定合理性。2.2 节中统计结果也表明,对于台阶式沉井类结构,这一经验化的近似是简单有效的,避免了等效墩宽计算过程中更多与局部冲刷相关的非沉井自身结构参数的引入,如流速U和粒径d。因此在预测台阶式沉井局部冲刷深度时,使用式(5)计算等效墩宽更为合理。

图8 冲深墩宽比统计直方图Fig.8 The statistics histogram of ratio of scour depth and pier width
虽然式(5)形式简单,在经验上能够较好地描述动床条件下台阶式沉井的平均阻水宽度,但其计算结果逻辑上仍存在一定问题。现有研究表明随着埋置深度的增大,局部冲刷深度呈现先减小后增大再不变的变化趋势[14,21]。根据等效墩宽的定义,等效墩宽大小也应呈现该变化趋势,但是式(5)计算结果显示等效墩宽会随着埋置深度增大而不断增大。由于当前尚未有较为合理的方法仅使用墩型自身结构参数对该变化趋势进行合理描述,因此台阶式沉井等效墩宽的准确计算仍待开展深入研究。
3 结 语
基于理论和试验数据分析,对深水桥梁台阶式沉井基础等效墩宽的计算方法进行了对比分析,得出以下结论:
1)对于台阶式沉井类结构等效墩宽计算,国内外方法均是通过阻水效应守恒条件推导得到的,《公路工程水文勘测设计规范》(JTG C30—2015)中计算墩宽公式主要考虑定床条件下的平均阻水宽度,而Melville和Raudkivi[11]等效墩宽计算公式则是针对动床条件下平均阻水宽度的近似。
2)开展台阶式沉井局部冲刷试验,根据试验结果对比了不同等效墩宽计算方法对于台阶式沉井的适用性,发现Melville和Raudkivi[11]的近似公式计算结果与实际平均阻水宽度最为接近。
3)收集了国内外193组台阶式沉井类结构局部冲刷资料开展分析,发现Melville 和Raudkivi[11]有效墩宽计算公式能够较好地量化台阶式沉井类结构的非均匀性,可适用于大多数细砂至粗砂地质条件下的台阶式沉井类桥墩。统计结果表明台阶式沉井类结构冲深墩宽比ds/D2平均值为0.945,体现了Melville 和Raudkivi[11]计算公式中使用的近似方法的合理性。

