电场力做功与路径无关的条件
王良翼
(成都市树德中学 四川 成都 610031)
柯丁荣
(四川省雅安中学 四川 雅安 625000)
顾 鑫
(西华师范大学物理与天文学院 四川 南充 637000)
王 娣
(烟台开发区高级中学 山东 烟台 264000)
向国兴 廖友兵
(成都市锦江区嘉祥外国语高级中学 四川 成都 610023)
在静电场中,电场力做功与路径无关,只决定于初末位置[1].此处电场力做功与路径无关的条件需要注意以下两点:第一,如果静电场是有界静电场,带电粒子从边界某点运动出静电场,然后从边界另一点再进入静电场,电场力做功可能与路径有关;第二,静止电荷周围产生的电场称为静电场[1].静电场中,任何一个点的电场不随时间变化,如果带电粒子在交变电场中运动,虽然某一时段为静电场,但是整个过程电场力做功可能与路径有关.在教学过程中发现学生知道电场力做功与路径无关,但是忽略做功与路径无关的条件,从而对带电粒子在电场中运动的复杂情境理解出现偏差.
1 题目及解析
【例题】如图1所示,在竖直面内的光滑半圆弧绝缘轨道与光滑水平绝缘轨道相切于B点,圆弧轨道左边有场强大小E=2×104N/C、方向与水平轨道成θ=37°斜向上的匀强电场.一个带电荷量q=+1×10-4C的小物块以初速度v0=16 m/s从A点开始运动,AB间距L=10 m.物块在运动过程中电荷量不变,圆弧半径R=4 m,物块质量m=0.2 kg,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=
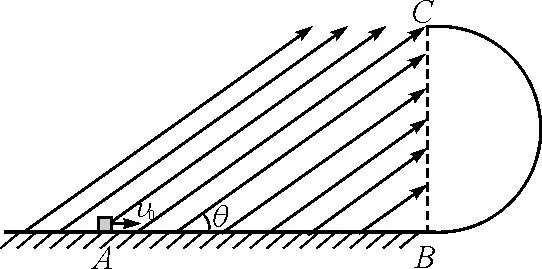
图1 有界电场分布示意图
0.8,求:
(1)带电物块通过C点时的速度大小;
(2)带电物块从C点抛出后在竖直方向和水平方向的加速度大小和方向;
(3)带电物块从C点抛出后落在水平地面时距A点的距离.
解析:(1)由题意从A到C对小物块由动能定理得
(1)
解得带电物块通过C点时速度大小为
v=16 m/s
(2)对小物块从C点抛出后受力分析可得
竖直方向有
mg-qEsin 37°=ma1
(2)
水平方向有
qEcos 37°=ma2
(3)
解得a1=4 m/s2,方向竖直向下,a2=8 m/s2,方向水平向右.
(3)带电物块从C点抛出后,设经过t时间落地,则竖直方向满足
(4)
水平方向满足
(5)
解得t=2 s,x=16 m.
如图2所示,落在水平地面的D点距A点的距离为

图2 带电物块运动示意图
Δx=x-L=6 m
(6)
2 带电粒子出进有界电场 电场力做功与路径有关
教学过程中,学生认为,电场力做功与路径无关,只取决于初末位置.如图3所示,由例题的第(3)小问可知,小物块落地点为D点,D点的速度为8 m/s,设AD的距离为Δx,从A点到D点的过程中,只有电场力做功,所以对小物块应用动能定理得

图3 电场力做功与路径的关系
(7)
解得Δx=12 m,与原文正解矛盾.
学生的错误理解在于对电场力做功与路径无关的条件把握不清.电场力做功与路径无关的条件是带电体一直需要在静电场中运动,如果带电体运动出静电场的区域再返回静电场区域,电场力做功与路径无关的条件则可能不成立.本题就是带电物块从B点运动出电场,然后再从C点进入电场,在电场中从点A到点B任选一条路径电场力做功与路径无关,在电场中从点C到点D任选一条路径电场力做功与路径也无关,但是不能认为带电粒子从A点运动到D点全过程中电场力做功与路径无关.带电物块从点A到点D运动过程中,电场力做功应该计算各段电场力做功之和.由图3可知,小物块从A点运动到B点电场力做功
WAB=EqLcosθ
(8)
小物体从B点运动到C点电场力不做功
WBC=0
(9)
小物体从C点运动到D点电场力做功
WCD=-Eq·2Rsinθ-
EqLcosθ-EqΔxcosθ
(10)
所以小物块从A点运动到D点整个过程中电场力做功为
WAD=WAB+WBC+WCD=
-Eq·2Rsinθ-EqΔxcosθ
(11)
从A点到D点的过程中,对小物体应用动能定理得
-Eq·2Rsinθ-EqΔxcosθ=
(12)
解得Δx=6 m,与原文正解相符合.
3 分时段静电场 电场力做功与路径有关
如图4所示,匀强电场的大小为E,方向水平向右,在A1点静止释放一带正电粒子,仅在电场力作用下,粒子运动到A2时,匀强电场大小不变,方向改变为水平向左,A1A2的距离为x,求粒子再次回到A1时的速度大小?
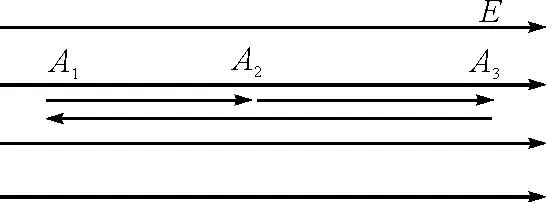
图4 分时段静电场示意图
教学过程中发现,很多学生认为粒子在电场中的位置没有变化,所以电场力没有做功,从而粒子回到A1点时,由动能定理,粒子的速度为零.静电场中,电场力做功与路径无关,这里的静电场只能是电场不随时间变化,而本题中的静电场方向突变之后,电场力做功与路径有关.由运动分析,对带电粒子应用动能定理得
(13)
解得
(14)
4 带电粒子出进有界分时段静电场 电场力做功与路径有关
如图5所示,是回旋加速器的示意图.

图5 回旋加速器加速示意图
在回旋加速器中,粒子在A1处,电场的方向竖直向下,粒子运动到A2处,电场的方向也是竖直向下,如果认为电场力做功与路径无关,选择如5图所示水平向左的路径,从A1到A2电场力没有做功,所以A1点的速度和A2点的速度一样,从而回旋加速器不能达到加速的目的.这种理解是错误的,第一,回旋加速度器中的静电场为交变电场;第二,带电粒子运动出电场,然后在磁场中运动,再进入电场,所以回旋加速度器中粒子运动全程做功与路径有关.设半圆形金属盒的距离为d,则由动能定理得
(15)
从而在回旋加速器中,粒子的速度越来越大.
5 总结与反思
电场力做功与路径无关的条件是带电粒子在静电场中运动,如果带电粒子运动出静电场的边界,然后从非等势点进入静电场,电场力做功与路径有关.同时静电场特指全过程中电场不是时间的函数,不然带电粒子在变化的电场中,电场力做功也与路径有关.

