关于“利用手机Phyphox软件探究向心加速度公式”实验的再思考

张明硕 黄致新

(华中师范大学物理科学与技术学院 湖北 武汉 430079)

智能手机的普及促进了手机传感器在物理教学中的应用,在向心加速度的教学中,学生可以利用手机的加速度传感器和陀螺仪分别测出圆周运动物体的向心加速度和角速度的大小,并通过Phyphox软件将数据可视化并以XLS等表格格式导出,对数据进行分析可以有效得出向心加速度公式．

为了挖掘出“利用手机Phyphox软件探究向心加速度公式”这一实验更加丰富的教学功能,让此实验更好地应用于中学教学中,笔者结合具体实验与相关文献对其进行再思考,并就相关问题做进一步阐释与澄清．

1 实验验证和探究的逻辑

为了找出向心加速度、转动半径、角速度三者的关系,探究或验证向心加速度公式,我们一般会用到控制变量法对所需数据进行测量[1-3]:控制转动半径r大小不变,改变角速度ω大小,测得相应的向心加速度a,得出a-ω关系为a=k1ω2;同理,控制ω一定,得出a-r关系为a=k2r;然后从a=k1ω2和a=k2r推导出向心加速公式为a=rω2．

关于上述推导过程,笔者认为需要对其中的逻辑做进一步论述．根据a=k1ω2和a=k2r如何推导出a=rω2,以及推导过程所体现的逻辑是对公式a=rω2的验证还是探究呢?

1.1 对公式进行“验证”

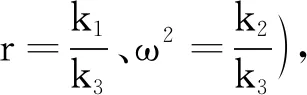
1.2 对公式进行“探究”

在未知向心加速度公式的情况下,从逻辑上讲,a=k1ω2和a=k2r还不足以推断出公式a=rω2,因为k1和k2为什么不可能是某个还未探讨的物理量呢?但是从物理学研究的一般过程而言,物理学的探究也需要基于事实和有所根据的猜想,从a=k1ω2和a=k2r是可以猜想出公式a=rω2的．在教学中需要引导学生对斜率值进行观察,发现a-ω2(a-r)图像的斜率值与转动半径(角速度的平方)的大小在误差允许范围内相等,即k1=r、k2=ω2,环环相扣,进而顺利猜想出a=rω2,再利用多组数据重复检验,最终确认向心加速度公式为a=rω2．这样即强调了物理核心素养“科学探究”中的证据要素[4],又能让学生从问题到猜想再到验证,最终得出结论,加深学生对物理学研究过程的理解．

2 传感器位置的确定方法

本文实验需要用到手机中的加速度传感器和陀螺仪．陀螺仪的位置难以确定,因为在同一转速下,手机上任何地方的角速度大小均相等,换言之,陀螺仪的位置并不会对角速度的测量值产生影响．但是,手机上不同位置的加速度大小是不相等的,这使得确认加速度传感器的位置成为必要．

笔者按图1所示对器材进行组装,将手机水平放置在圆盘上进行实验,设计了两种确认加速度传感器位置的方法．

图1 器材组装图

2.1 弧线相交法

如图2所示,为弧线相交法找到的手机加速度传感器位置.具体操作如下.

图2 弧线相交法

将手机任意摆放在某一位置,改变角速度,绘制a-ω2图像.图像拟合出的斜率值,即为转动半径大小,也就是加速度传感器到圆心的距离,记为r1,围绕圆心以r1为半径画圆在手机上留下一段弧线;改变手机位置,重复操作,以r2为半径在手机上留下另一段弧线;两段弧线的交点即为加速度传感器的位置．

由于长度测量工具的精度限制和人为操作的误差,笔者只能大致确认实验所用手机的加速度传感器位置在前置摄像头附近．

2.2 直线相交法

为了导出向心加速度大小的测量值,笔者和文献中的实验设计用到的多为图3所示的“向心加速度”模块．跳出思维定势,向心加速度本质上仍然是加速度,我们不妨利用图4所示原始传感器中的“加速度(不含g)”模块导出相关数据．

图3 “向心加速度”模块

图4 “加速度(不含g)”模块

“加速度(不含g)”模块可以显示x、y、z轴3个方向的分加速度以及合加速度的大小,手机的x、y、z轴如图5所示．将手机平放在水平圆盘上转动,忽略z轴方向的加速度,只考虑x轴与y轴方向的加速度．

图5 Phyphox手机坐标系

实验时任意摆放手机使其做匀速圆周运动,向心加速度为x轴与y轴两个方向的加速度的矢量合成,向心加速度大小即为图4中“加速度绝对值”的大小．

那么如何利用“加速度(不含g)”模块确定加速度传感器的位置呢?

我们知道,物体做匀速圆周运动时的加速度指向圆心,不存在沿切线方向的切向加速度．通过改变手机的摆放位置,使x轴方向的加速度为零(由于误差的存在,确保x轴方向加速度值在零附近波动,平均值大致为零即可),这样y轴指向圆心,y轴方向的加速度即为向心加速度,过圆心垂直手机x轴在手机上留下一段直线;同理,使y轴方向的加速度为零,x轴方向的加速度即为向心加速度,过圆心垂直手机y轴在手机上留下另一段直线,两条直线的交点即为传感器的位置．用此方法同样确定所用手机的加速度传感器位置在前置摄像头附近,与“弧线相交法”得出的结果一致．

3 切向加速度对测量的影响

在文献[1-3]中,根据控制变量法测量数据时,是让手机做匀速圆周运动,待ω值稳定在某一数值附近时,才进行取值,并记为ω1,然后改变转速,以同样的方式依次得出ω2,ω3,ω4,…,根据数据绘制的a-ω图像是一个个离散的点,每一个ω值对应的均是某次匀速圆周运动的角速度大小．因此,准确地讲,文献[1-3]利用测得的数据得出的公式a=rω2是匀速圆周运动的向心加速度公式．

那么,是否可以如匀速圆周运动一样,对变速圆周运动的向心加速度公式进行探究呢?

文献[5]利用Phyphox软件探究向心加速度公式时,是从慢到快摇动自行车脚踏板,使固定在车轮上的手机做角速度不断变大的圆周运动,测量出连续变化的角速度的值,因此得到的a-ω2图像是一系列较为密集的点．考虑到Phyphox软件数据采样的时间间隔很短,我们可以将文献[5]中a-ω2图像近似看成是连续的．因此,文献[5]根据数据探究的其实是变速圆周运动的向心加速度公式,得出的结论同样为a=rω2．

从实验结果来看,无论是变速圆周运动还是匀速圆周运动,利用各文献所展示的数据得出的向心加速度公式均为a=rω2．

从物理意义上讲,运用极限思想,变速圆周运动可以看成一系列匀速圆周运动的连续变化,所以变速圆周运动和匀速圆周运动的向心加速度公式是一致的．

但是,根据Phyphox软件对“向心加速度”模块的介绍,笔者发现,手机做变速圆周运动时,如何对向心加速度进行测量还需要进一步探讨．

3.1 基于“向心加速度”模块的测量

查看Phyphox软件对“向心加速度”模块的介绍,得知此模块显示的向心加速度大小其实是加速度计得到的“加速度绝对值”的大小．换言之,将手机水平放置在圆盘上进行实验,“向心加速度”模块显示的加速度值其实是x轴与y轴两个方向的分加速度经矢量合成后的合加速度的大小．

手机做匀速圆周运动时,传感器没有切向加速度,只有指向圆心的加速度,“向心加速度”模块显示的加速度值是真实的向心加速度的大小．

但是,手机做变速圆周运动时,传感器存在切向加速度,如图6所示.

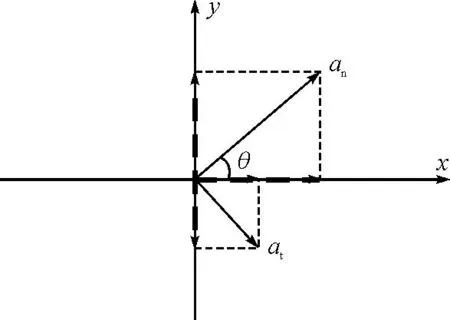
图6 变速圆周运动的加速度

以传感器位置为原点,建立直角坐标轴．根据

ax=ancosθ+atsinθ

和ay=ansinθ-atcosθ

不难计算出

从实验效果来看,即使存在切向加速度,利用“向心加速度”模块导出的数据也能很好地符合公式a=rω2．这可能是因为Phyphox软件每次采集数据的时间间隔很短,切向加速度很小,对向心加速度大小的测量影响有限．同时,这也正好证明了“变速圆周运动是一系列匀速圆周运动的连续变化”这一物理事实．

在变速圆周运动中,切向加速度的存在会影响Phyphox软件“向心加速度”模块显示的加速度值,那么是否可以消除切向加速度对向心加速度测量值的影响呢?换言之,手机做变速圆周运动时,如何显示出真正的向心加速度?

3.2 基于“加速度(不含g)”模块的测量

参考关于“直线相交法”的讨论,我们可以通过调整手机的摆放位置,让x轴(y轴)指向圆心,而y轴(x轴)指向圆周运动的切线方向．这样即使是变速圆周运动,也能排除切向加速度对向心加速度测量值的影响,x轴或者y轴方向的加速度值即为向心加速度的大小．

4 结束语

利用智能手机传感器开发的学生实验,具有成本低、精度高等特点,将其应用于中学课堂之中,可以获得良好的教学效果．在教师的引导下,学生能够自主完成“利用手机Phyphox软件探究向心加速度公式”实验,得出向心加速度的公式．

除了完成知识的传授、让学生理解向心加速度公式之外,本文倡导应挖掘此实验更加丰富的教学功能．

明晰验证性实验和探究性实验的逻辑,可以培养学生对问题进行科学推理、科学论证的能力,尤其是将此实验作为探究性实验应用在教学中,可以让学生对物理研究的一般过程有更加深入的理解．在探究过程中,基于证据提出猜想并严格地对猜想进行检验,明白物理学既是严谨的科学,同样也是猜想的艺术．

确认加速度传感器的位置,不仅能让学生了解手机传感器和Phyphox软件工作的原理,还能让学生对向心加速度公式进行应用,加深其对匀速圆周运动、向心加速度的方向和大小的理解,促进学生关于运动的物理观念的构建．

讨论切向加速度的存在,让学生的认知从特殊的匀速圆周运动上升到更为一般的变速圆周运动．利用极限思想,在理论上可以认为变速圆周运动是一系列连续的匀速圆周运动的集合,但是学生不易理解变速圆周运动和匀速圆周运动的这一关系．利用手机传感器和Phyphox软件对变速圆周运动的向心加速度公式进行探究,得到了和匀速圆周运动一样的结果,正好在实验上为这一关系提供了事实证明．学生由此可以体会到物理知识在理论和实验上的和谐统一,对实验这一物理研究方法的理解也更为深刻．