带有NLOS误差补偿的UWB/INS室内融合定位算法研究

唐新明，王鹏，张茂帅

（青岛大学自动化学院，山东青岛 266071）

近年来，随着智能设备和技术的普及，人们对各种基于位置服务(Location Based Services，LBS)的需求日益增加[1]，如自动驾驶、应急救援、人员管理、智慧工厂、无人超市等。由于建筑物遮挡，全球卫星导航系统无法在室内环境中提供可靠的位置服务[2]，推动了Wi-Fi 定位、蓝牙定位、ZigBee 定位以及UWB 定位等[3]室内定位技术的发展。其中，UWB 技术具有时间分辨率高、穿透力强、抗多径性能好等优势，成为了当前室内定位领域的一种主要技术[4]。然而室内环境复杂多变，UWB 信号易受人员、物体或墙壁等因素的遮挡造成非视距(Non-Line-of-Sight,NLOS)传播，导致UWB 定位技术出现精度低和稳定性差等问题[5]。因此，在复杂环境下仅仅依靠单一类型的传感器很难实现高精度的定位。

INS 是一种独立的导航系统，通过惯性测量单元(Inertial Measurement Unit,IMU)来估计位置。IMU 不依赖外部信息，抗干扰能力强，但长期工作会产生较大累积误差[6]。因此，将UWB 和IMU 组合起来进行优势互补的融合定位算法被广泛研究。文献[7]提出了一种基于四元数卡尔曼滤波器的UWB/IMU 室内融合导航方法，避免了复杂的线性化，降低了系统的复杂度。文献[8]通过机器学习识别UWB 测距信息中的非视距误差，然后融合IMU 信息缓解NLOS 对定位精度的影响，缺点是需要保留大量离线数据。文献[9]提出了一种基于迭代卡尔曼滤波的融合定位算法，该算法利用三角不等式原理检测非视距测量值，在无连续非视距误差时具有较好的定位精度。然而,在实际室内环境中，经常出现多个UWB 设备同时并长时间处于非视距环境的情况，导致UWB 定位系统失效，无法校准IMU 的累积误差，进而影响融合定位系统的定位精度和稳定性。

针对以上现状，该文基于无迹卡尔曼滤波(Unscented Kalman Filter,UKF)提出了一种带有非视距误差补偿的UWB/INS 室内融合定位算法(UKF with NLOS Error Compensation,EC-UKF)。该算法不需要环境先验信息，仅使用UWB 测距信息通过残差检验法[10]即可识别非视距误差；同时通过构造“近似补偿误差”实现对非视距误差的高精度补偿，从而保证UWB 定位系统的稳定运行。实验数据表明，所提算法在具有连续非视距误差的强NLOS 环境下依旧能保持较高的定位精度和稳定性。

1 系统模型

1.1 基于INS的运动模型

INS 通过IMU 来估计位置，其定位原理如图1所示。

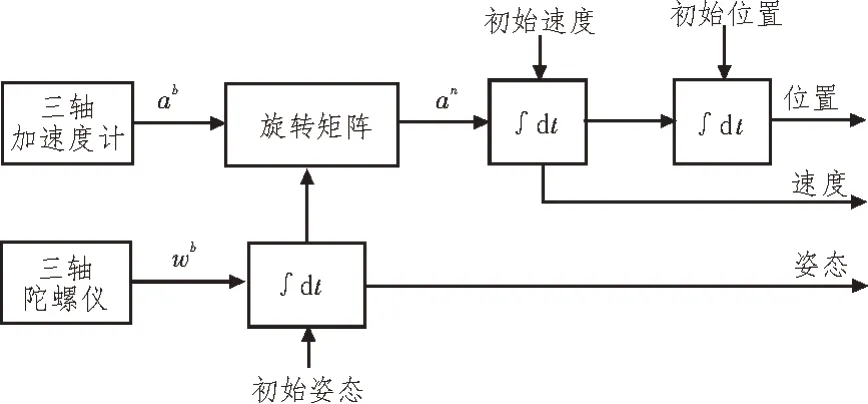
图1 IMU定位原理示意

该文采用“东-北-天”坐标系作为导航坐标系，载体坐标系采用“右-前-上”坐标系，利用位置、速度、四元数[11]来描述组合定位系统的运动状态。因此，组合定位系统的运动模型为：

其中，pn为导航坐标系中的三维位置向量；vn为导航坐标系中的三维速度向量；qbn为方向四元数；a͂b为载体坐标系下加速计测量值；ῶb为载体坐标系下陀螺仪测量值；ba和bg分别为加速度计和陀螺仪偏差向量；na和ng分别为加速度计和陀螺仪的测量噪声；δa和δg分别为加速度计和陀螺仪偏差的随机游走噪声；g为当地重力加速度；⊗为四元数乘积运算符[12]；为从机体坐标系到导航坐标系的旋转矩阵[13]。

1.2 观测模型

基于UWB 的室内行人定位系统由四个位置已知的UWB 基站、一个待定位UWB 标签、一个无线数据传输通道和一个上位机组成，如图2 所示。

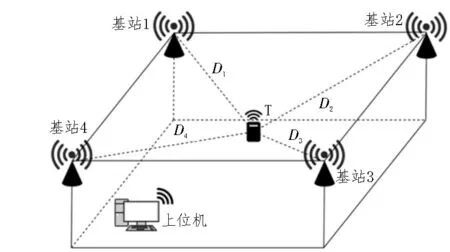
图2 超宽带定位系统

为减少基站和标签之间时钟不同步以及频率漂移而产生的测距误差，采用基于到达时间(Time of Arrival，TOA)的双边双向测 距(Double-Sided Two-Way Ranging，DS-TWR)方法[14]测量标签与基站之间的距离。

基于图2 所示的UWB 定位系统，利用多边定位算法可以得到组合定位系统的观测模型为：

其中，D1,k、D2,k、D3,k和D4,k分别为时刻标签到四个基站的距离；(px,k,py,k,pz,k)为k时刻标签的位置；nuwb,1、nuwb,2、nuwb,3和nuwb,4分别为四个基站的测量噪声；(xi,yi,zi)为基站坐标，i=1,2,3,4。

2 基于EC-UKF的融合算法设计

2.1 NLOS误差识别与补偿

在室内行人导航系统中，相邻时间的UWB 测距值总是相似的。然而NLOS 会造成正传播延迟，导致NLOS 环境下的测距误差远大于LOS 环境。通过设定决策阈值[15]，利用残差检验法识别NLOS 误差，可以在没有先验信息的情况下区分出LOS 和NLOS 数据。具体过程如下：

令ΔDj,k=Dj,k-Dj,k-1,j=1,2,3,4为k时刻第j个UWB 基站的测距残差。

则NLOS 识别方法为:

其中，TH 为决策阈值，大小由标签的移动速度和LOS 环境下UWB 测距的标准方差决定。通常选择TH=σ+Δs，其中，Δs为标签在测距时的位移。

为了提高定位系统的定位精度和鲁棒性，当第k时刻的测量值为NLOS 数据时，使用第k-1 时刻的测量值对其进行补偿。

在考虑NLOS 误差补偿时，UWB在k时刻的测量数据可以表示为：

设Δk为补偿NLOS 数据后估计结果的误差，其计算公式如下：

其中，hk(Xk)=[h1,k,h2,k,h3,k,h4,k]T表示第k时刻UWB 标签和各基站之间的欧氏距离。

对于室内行人的实时导航与定位，在正常情况下，系统状态的变化和误差Δk通常都是可以忽略的。然而，在NLOS 环境下误差Δk将持续增加，这将影响补偿NLOS 数据的准确性。因此，计算补偿NLOS数据后估计结果的误差Δk是有必要的。令Xk-1等于k-1 时刻的后验状态估计值，并且令Xk等于k时刻的估计值。的值通常是已知的，但是̂k的值未知且无法计算。因此，考虑使用-1的一步预测值̆k来近似̂k，则近似补偿误差Δk计算如下：

因此，考虑近似补偿误差Δk的NLOS 修正数据可以表示为：

2.2 EC-UKF融合定位算法

卡尔曼滤波器最早是处理线性滤波问题的一个最小方差估计器。然而实际生活中许多系统都是非线性系统，由此发展出了扩展卡尔曼滤波、无迹卡尔曼滤波等可以处理非线性滤波问题的卡尔曼滤波器。其中，UKF 通过无迹变换(Unscented Transformation,UT)[16]近似非线性系统状态的后验概率密度分布，避免了计算雅可比矩阵的需要[17]，具有相对较低的计算开销和较高的估计精度。

该文设计了基于EC-UKF 的UWB 和IMU 融合定位算法。在滤波更新阶段，当UWB 系统出现非视距测量时，通过上述补偿算法对NLOS 误差进行补偿，以此提高融合定位系统的定位精度和稳定性，算法流程如图3 所示。

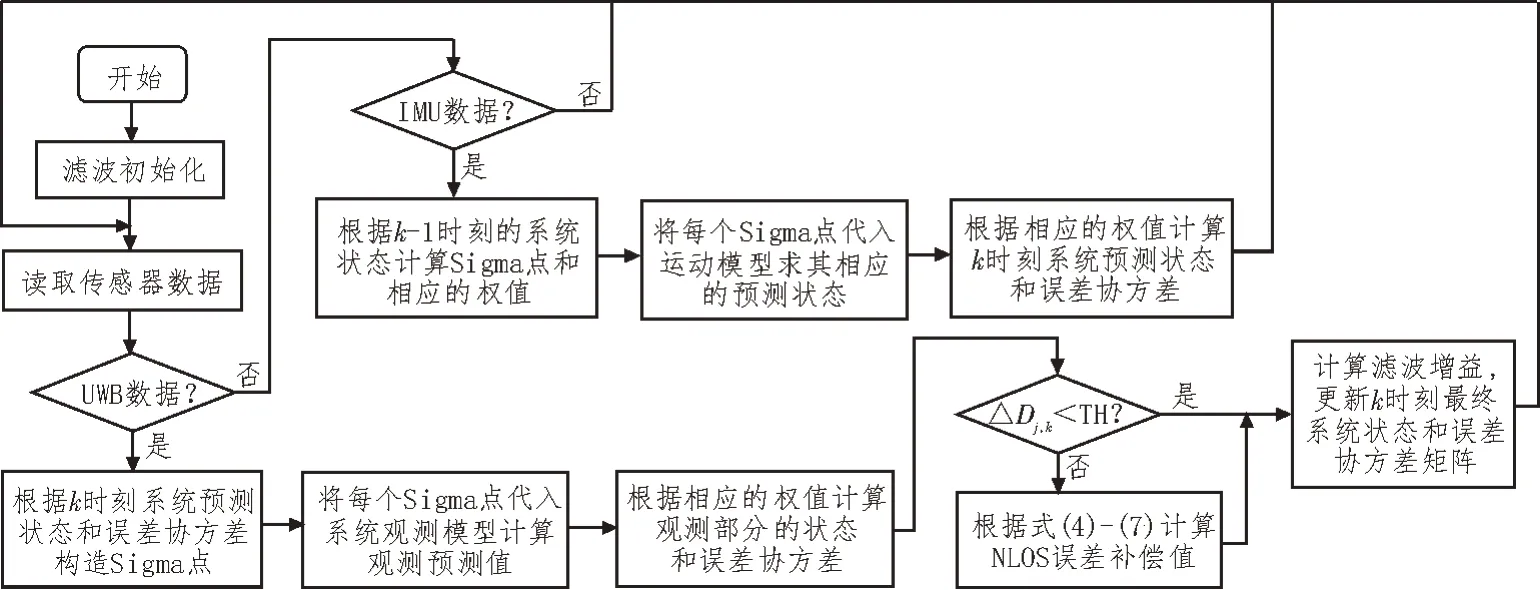
图3 EC-UKF算法流程图

3 实验与结果分析

3.1 实验环境及实验装置

为验证所提算法的有效性，在山东高速西海岸中心B1 层车库进行了实地实验。实验场景如图4所示。

图4 实验环境

其中，四个UWB 基站分布在矩形的四个顶角，分别固定在高2 m 的三角支架上；实验区域中间为两根混凝土承重柱，用来构造NLOS 环境；预设运动轨迹如图4(b)虚线所示，是一个长12.9 m、宽4.7 m 的矩形轨迹。

实验采用Decawave 的UWB 收发器DW1000 以及意法半导体的六轴惯性测量单元LSM6DSL。实验中UWB和IMU的采样频率分别为20 Hz和100 Hz。

3.2 实验结果及分析

图5 是所提出的EC-UKF 融合定位算法与单独使用UWB 或IMU 定位方法的定位结果对比。

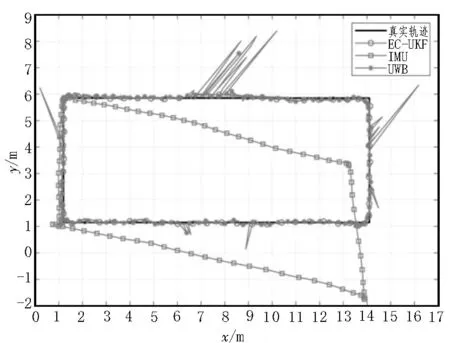
图5 EC-UKF算法与单一传感器算法的定位结果对比

从图5 可以看出，EC-UKF 融合定位结果明显优于单一传感器的定位结果。在NLOS 环境下UWB 定位轨迹波动较大，且在遮挡严重处出现较大的“毛刺”；受累积误差的影响，IMU 定位轨迹在实验开始不久便出现较大偏移，无法进行正常定位。

图6 是EC-UKF、UWB、IMU 三种定位算法的定位误差累积分布函数。

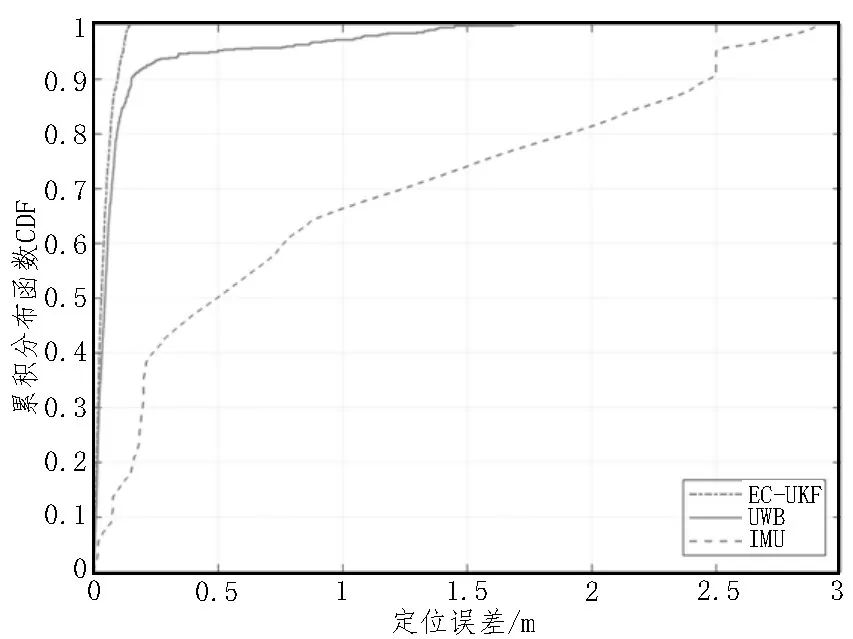
图6 EC-UKF、UWB、IMU三种定位算法的误差累积分布函数

由图6 可知，与单一传感器定位方法相比，ECUKF 算法的最大误差和均方根误差更小，定位精度相较于UWB 定位提高了84.15%，相较于IMU 定位提高了96.16%，具体数值如表1 所示。

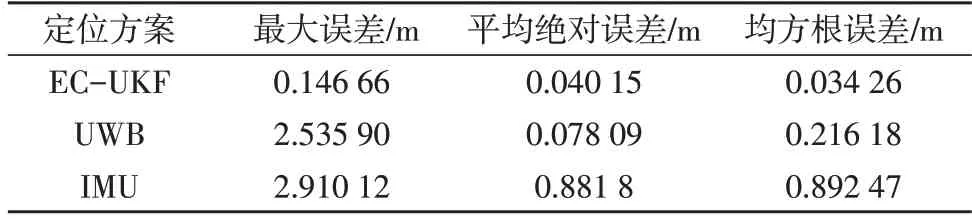
表1 三种定位算法的定位误差

图7 是EC-UKF 融合算法、EC-EKF 融合算法与传统UKF 融合算法的定位结果对比。

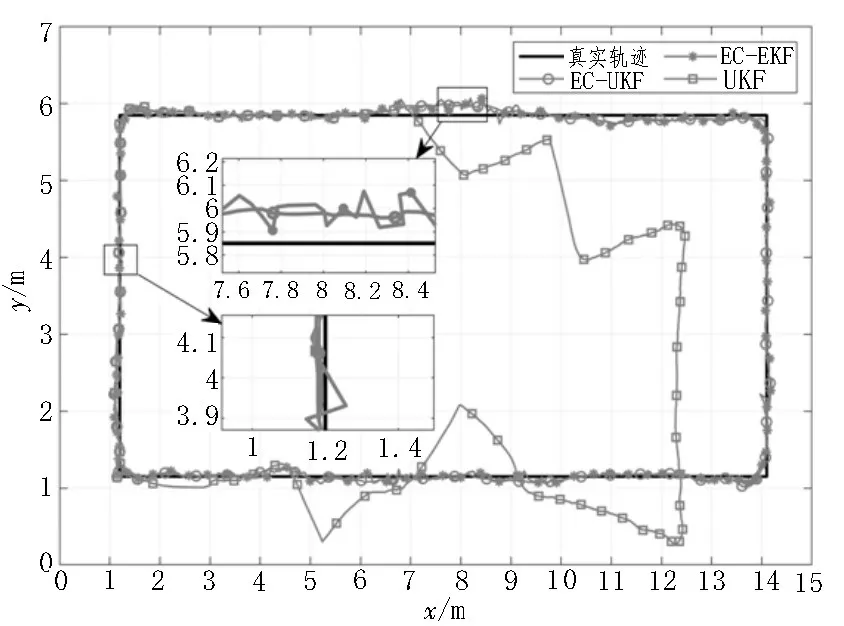
图7 EC-UKF、EC-EKF与UKF算法的定位结果对比

从图7 可以看出，EC-UKF 和EC-EKF 算法定位性能相近，但是所提出的EC-UKF 算法定位轨迹更加平滑，精度更高；传统UKF 融合算法在弱NLOS 环境下性能与EC-UKF 相近，而在强NLOS 环境下定位轨迹出现较大偏差，并且之后即使UWB 通信恢复正常，但IMU 累积误差没有得到校正，导致定位轨迹偏离真实轨迹。

图8 是EC-UKF、EC-EKF、UKF 三种定位算法的误差累积分布函数。

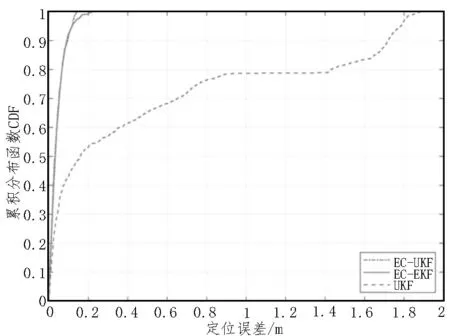
图8 EC-UKF、EC-EKF、UKF三种定位算法的误差累积分布函数

由图8 可知，EC-UKF 与EC-EKF 性能相近，但是EC-UKF 的最大误差与均方根误差更小，定位精度相较于EC-EKF 提高了9.58%，相较于传统UKF提高了94.71%，具体数值如表2 所示。

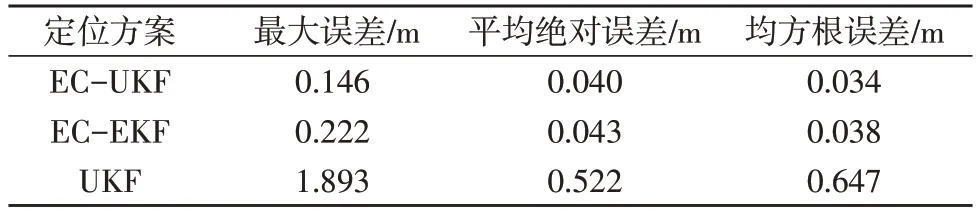
表2 三种定位算法的定位误差

4 结论

针对复杂室内环境中，UWB 定位精度易受非视距影响导致误差增大以及INS 定位误差随运行时间迅速累积的问题，提出了一种基于EC-UKF 的UWB/INS 室内融合定位算法。该算法没有忽略由障碍物遮挡引起的非视距误差，而是利用INS 预测信息计算出“近似补偿误差”，然后结合UWB 测距信息估计和补偿非视距误差，从而缓解非视距环境对组合系统定位精度的影响。实验结果表明，在具有连续非视距的强NLOS 环境下，EC-UKF 算法依旧能保持较好的定位精度和稳定性。