基于支持向量机的网格化电网负荷预测算法设计

徐良德，郭挺，雷才嘉，陈中豪，刘恒玮

（广东电网有限责任公司广州供电局，广东广州 510600）

电网负荷指的是某一特定用电单位或用电区域所使用的电能总和。而电网短期负荷预测[1-3]则是指以小时、天、周和月等为单位，对电网未来某时间段内的负荷数据进行预测，且对其准确预测可为电力部门的后续输电策略提供有力支持。通常电网负荷的预测方法是通过利用过往数据来进行推断及预测，但由于其具备不确定性，使得预测结果会受未来各方面因素的影响。传统电网负荷预测依靠专家决策的方法，通过以往的数据及经验对未来用电量进行判断。该方法的适应度较差，因此预测精度通常难以满足要求。尤其在电网智能化的大趋势下，网格化管理势在必行，而这样则会产生更大规模的用电数据[4-6]。

该文使用改进的支持向量机（Support Vector Machine，SVM）算法来实现网格化电网负荷的短期预测。该算法可快速对多数量、小样本集合进行拟合与预测，同时还具有良好的性能，可以满足某地区网格化电网的负荷预测需求。

1 模型构建

1.1 基于SVM算法的数据分类模型

支持向量机是一种数据分类算法，该算法起源于统计学，能通过函数的拟合对有限数据加以训练，进而得到训练结果。其可训练线性及非线性数据，且算法所需的样本数量较少，同时数据特征的抓取能力也较强。

SVM[7-8]由线性学习机发展而来，该运算的本质即将样本数据映射至一个二维平面，再通过预设的平面分割函数对该平面进行分割。而分割所期望达到的结果，便是最大限度地将不同类别的数据进行切分，具体示意图如图1 所示。

假设最优平面为H；样本集合为(xi,yi)，i=1,2,3,…,n；x向量的维度是m；y则表示数据的类别，通常使用1 或-1 表示。而在图1 中，可见H平面将不同类别的数据分为了两个部分。若方块表示的数据类别为1，圆形为-1，则H平面可表示为：

式中，ω为权值，b为阈值。

除了最优平面H外，图中还有两个与其平行的平面H1及H2。假设H1面的数据点是x，该点投影至最优平面H的点为x0，而H1与H面的距离为γ，ω表示垂直于面H且指向面H1的向量，则上述参数间的数学关系如下：

样本点xi到最优平面距离的最小值为：

最终目标函数可确定为maxd，则转化得到的优化方程就可以表征为：

式中，C为算法惩罚因数，ξi为松弛因数，s.t.则是函数的约束条件。除了图1 所示的数据外，在实际应用中，若样本数据处于相同平面，还需将数据映射至高维空间中。常用的方法即为增加核函数，具体如下：

式中，核函数为U(·)，Φ(·)·Φ(·)为最优平面的内积。此时式（4）的问题可转化为式（6）所示的函数：

由以上计算过程可得到最终的决策函数，具体如下：

其中，和b*是参数最优经验值。

基础SVM 算法的执行过程如图2 所示。

图2 SVM算法执行过程

1.2 基于PCA-PSO的SVM参数优化算法

由SVM 可知，在算法执行过程中，最重要的步骤是选择合适的参数，例如惩罚因数C、投影距离γ及核函数U(·)等。SVM 模型的性能与此类参数的相关性较大，但这些参数的最优值是未知的，故需对最优参数进行搜索。传统的方法为多次仿真SVM 模型使用网格类搜索算法。然而该算法的参数搜索时间较长，同时收敛度也较差。因此，文中对粒子群算法（Particle Swarm Optimization，PSO）进行优化，且对SVM 参数进行最优选取。

PSO[9-11]是一种启发式算法，其将鸟类的捕食行为作为参照，使算法通过不断迭代以优化粒子的最佳位置。同时还采用粒子群中的特征信息完成共享，从而进一步提升算法的准确度。

首先PSO 执行初始化，并通过一定规则的迭代获得结果。在迭代过程中，需搜索个体与全局极值两个粒子，之后再对迭代速度及二次迭代值进行确认。假设集合样本数量为m，数据维度为d，而样本为Xi=(xi1,xi2,…,xid)，i∈(1,m)，迭代发生的速度则是Vi=(vi1,vi2,…,vid)，i∈(1,m)。若搜索后得到的局部最佳粒子位置为Qi=(qi1,qi2,…,qid)，而种群所有粒子内部的最佳位置为Qall=(qall1,qall2,…,qalld)，最终可得到粒子的更新速度如下：

式中，c1、c2为加速因数，r1、r2为随机数，k为迭代次数。最终得到的下一代粒子为：

PSO 算法的执行流程如图3 所示。

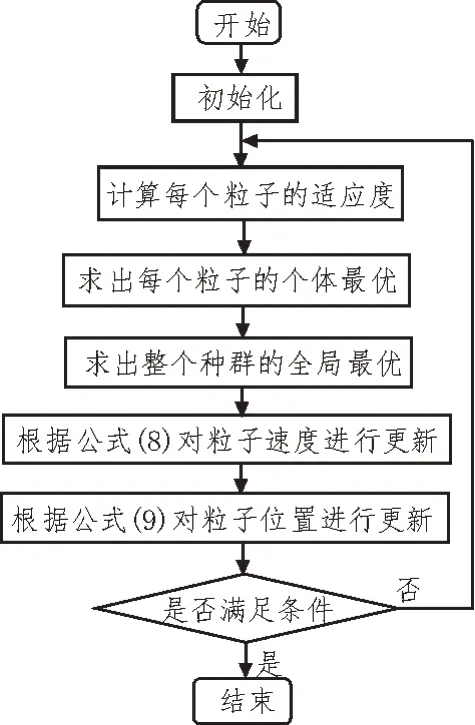
图3 PSO算法执行流程

PSO 可对SVM 参数进行优化与训练，但若数据的维度较高，在对一些含有噪声的信息进行训练后，则易出现拟合过量及特征种类提取不完整的问题。因此，需进一步提取数据特征。

主元分析法（Principle Component Analysis，PCA)[12-14]是一种降低数据维度的算法。其可通过多种类的数据完成主要指标的提取，进而实现样本数据从高维到低维空间的转变，同时还能降低算法的冗余度。

假定样本数据数量为m，数据维度为d，样本为Xi=(xi1,xi2…xij)，i∈(1,m)，j∈(1,d)，则此时样本数据可用m行d列的矩阵表示为(Xij)m×d。

通过多维数据对主成分特征进行提取，可由以下步骤执行：

1）矩阵标准化。对数据矩阵(Xij)m×d进行标准化，则有：

2）计算的协方差矩阵，并对其进行分解，最终得到矩阵特征值集合λ=[λi]及特征向量集合A=[Ai]，i∈(1,n)。

3）计算矩阵的解，并获得各个特征向量的单特征贡献率及多特征累计贡献率。则有：

基于PCA-PSO 的SVM 参数优化算法流程如图4 所示。

图4 PCA-PSO算法的SVM参数优化算法流程

从图4 中可见，程序分为数据处理及预测两个部分。其中数据处理模块包括PCA 与PSO 算法，该模块主要对采集到的电力负荷数据进行取样，并提取其特征，从而降低数据维度带来的冗余度。然后，再利用PSO 模型对SVM 参数进行优化选取。而数据预测部分则将PSO 优化得到的参数传入至SVM 模型中，且对负荷数据进行训练，最终完成电力负荷数据预测。

2 算法测试

2.1 测试环境

文中采用的电力负荷数据集合为某地区2020—2021 年的用电数据及环境、日期、经济信息等。将其作为训练与验证数据集，则实验环境配置与样本集数据信息，如表1 所示。

表1 实验环境及样本集数据

2.2 PCA主源特征提取

该文首先使用PCA 来分析原始样本数据，并对影响电力负荷的各个特征因素进行训练及排序。然后，计算各特征向量的单特征贡献率与多特征累计贡献率，训练结果如图5 所示。

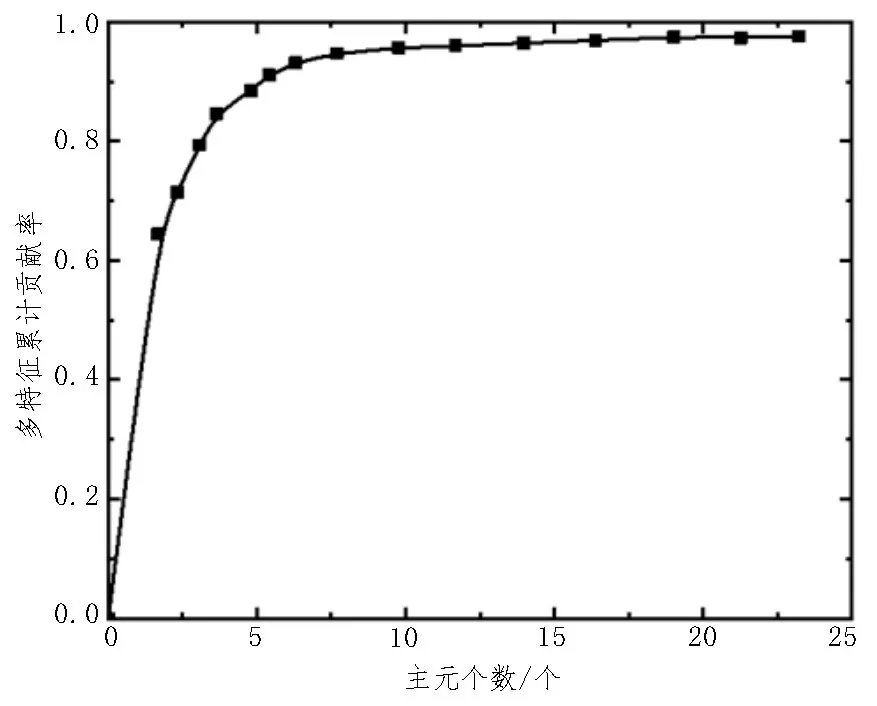
图5 训练结果

由图5 可知，随着主元个数的增加，多特征累计贡献率也逐渐提升。为了保证特征提取的准确性，此次选取的累计贡献率为91%，而特征个数则为6 个。具体特征类型如表2 所示。

表2 特征类型

2.3 预测实验

为验证模型的性能，使用经典算法SVM、PSO-SVM[15]、高斯回归过程（Gaussian Process Regression，GPR）[16]进行对比。同时算法最大迭代次数为100，其他参数则使用默认值，且所有算法均采用相同的数据集与完全一致的训练方式。此外，训练数据集合选择2020 年连续10 d 内的电力负荷数据，而验证数据集选择了2021 年的相同时间段。该文算法首先利用PSO 对SVM 参数进行训练，获得最佳参数后，再使用测试集合所具备的特征类型作为输入变量，进而得到最终的实验结果，如图6 所示。

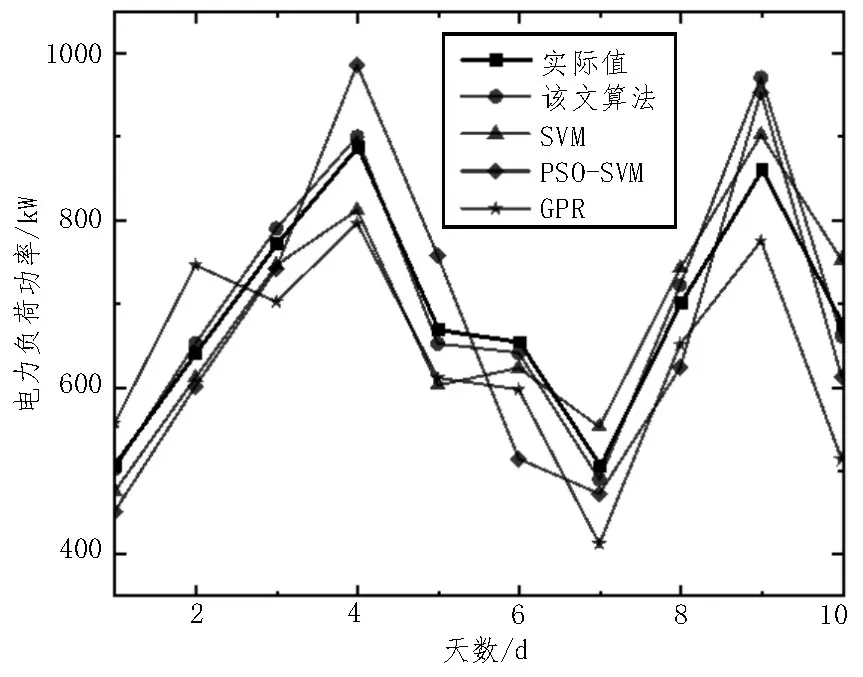
图6 实验结果示意图

从图6 可看出，该文算法模型的性能指标较优，预测的结果也更贴近真实值。相比之下，其他算法的预测结果则在曲线贴合度上与实际值存在一定的差距。这说明所提算法的预测精准度较优，能够对短期电力负荷数据进行精准预测。

为了定量分析预测结果，使用均方根误差（RMSE）、平均绝对误差（MAE）及平均绝对百分比误差（MAPE）进行评估。最终结果如表3 所示。

表3 误差计算结果

由表3 可看出，该文算法的三项指标均较为理想，这也从侧面证明了该算法的准确性较高。

3 结束语

该文提出了一种可用于短期网格化电网负荷预测的PCA-PSO-SVM 模型。该模型在经典粒子群算法的基础上加入了主元分析法进行改进，随即使用改进后的PCA-PSO 模型对SVM 关键参数加以训练，最终通过实验证明了所设计算法的有效性。实验结果显示，与其他算法相比，该文算法在RMSE、MAE及MAPE 三项指标中的误差均为最小。由此表明算法的性能较优，能够为短时间内的电力负荷数据做出准确预测。