引导思考,启发教学:多角度拓展数学思维能力

⦿ 江苏省苏州市立达中学校 徐寅倩

实践证明,启发式教学法具有激发潜能、拓展思维和发展素养的功能.在初中数学课堂教学中,教师应结合学生的学科思维能力和学情,根据课程标准要求,由浅入深、由表及里、由易到难逐步创设质疑情境,引导学生主动存疑、探疑和释疑,积极自主地构建数学学科素养.因此,启发式教学是当下教学的一个重要研究课题,也是教师应该具备的一项基本技能.

1 启发式教学的出发点是激发学生的存疑

在研讨课的评议活动中,有人认为课堂上有师生的双边活动,学生能通过教师设置的一连串问题进行学习就是启发式教学.这是将“启发式”误认为“问答式”了,学生回答问题变成了过眼云烟,在脑海中不会存留丝毫知识的印迹,更谈不上激发潜能、拓展思维和发展素养了.真正的启发式教学是学生“会思维”,而不是简单的“在思考”,是一种在心灵上对数学知识的撞击,是能迸发出智慧火花的.因此,启发式教学并不是一种教学形式,而是一种教学手段和方法.

比如,在进行“认识三角形(2)”教学时,可以创设情境:(做一做)将橡皮筋的一端固定在△ABC的顶点A上,另一端点P从点B出发沿BC移动到点C．问题:在移动过程中,橡皮筋(线段AP)的位置不断变化,你认为哪些位置是特殊的?让学生经历操作、观察、推理、交流等,得到橡皮筋的另一端点P可以落在BC的中点,橡皮筋AP可以平分∠BAC,橡皮筋AP可以与BC所在的直线垂直.通过活动,启发了学生对图形运动过程中特殊位置的思考.因此,启发式教学的根本目的在于启发学生的自主思维,产生的质疑情境是“学生跳一跳能够摘到桃”的形式,学生在思考过程中完善数学知识的建模.

2 启发式教学的目标是驱动存疑、探疑与释疑

对于中学数学来说,多年的教学实践表明,真正能达到启发学生的预期目的,必须在教学中注重以下几个方面:

(1)启发学生对数学奥秘的强烈探究好奇心

启发学生热爱数学,这对于初中数学教学是至关重要的.初中生的好奇心是个人有所发现、学有所成的前提.只有抓住了初中生的好奇心,才能启发并稳固他们的探究兴趣.

比如,“多项式的因式分解”是苏科版七年级下册第九章第五节的内容,是在前四节整数乘法的基础上的延伸.以下为笔者在该节教学时的实录片段.

活动:探究什么是因式分解.

问题1计算:375×2.8+375×5+375×2.2.

学生思考并能回答:375×2.8+375×5+375×2.2=375×(2.8+5+2.2)=375×10=3 750．

师:这样计算的依据是什么?

生:乘法分配律的逆运算．

师:如果把这个算式中的375记为字母a,把2.8,5,2.2分别记为字母b,c,d,怎么表示这个运算?

生:ab+ac+ad=a(b+c+d)．

师:如果将这个式子反过来,就得到a(b+c+d)=ab+ac+ad,这是刚刚学过的整式乘法中的单项式乘多项式法则．而将多项式ab+ac+ad写成积的形式a(b+c+d),叫做多项式的因式分解．

像这样,把一个多项式写成几个整式的积的形式,叫做多项式的因式分解.

问题2下列各式由左边到右边的变形,哪些是因式分解,哪些不是?为什么?

(1)ab+ac+d=a(b+c)+d;

(不是)

(2)a2-1=(a+1)(a-1);

(是)

(3)(a+1)(a-1)=a2-1;

(不是)

(4)3x2-2x-1=(3x+1)(x-1)．

(是)

师:因式分解的概念可以归纳为两个要点.①对象:一个多项式;②结果:几个整式的乘积的形式．

学生的释疑途径可以多样化,但结果必须是唯一的.因此,启发式教学并非课堂提问,而是质疑情境的创设,存疑过程的引领.学生能在不同的释疑途径中领会学习数学的过程是随认知的不同而不同的,能将不同的思维融合、内化成为自身的数学学科素养.

(2)启发学生用数学的眼光去存疑

思维活动是从存疑开始的.启发式教学的知识生成之处都是通过教师创设质疑情境,引起学生存疑思考,随之引导学生善于存疑,在探疑过程中多问为什么,这样就有可能从对生活、生产的观察中不断养成存疑、探疑的好习惯.有了这样的素养,课堂教学中的自主活动就很容易组织和开展了.

例如,在学习七年级上册第五章第三节“展开与折叠”时,一位教师的优质课课堂实录片段如下:

教师引导:出示一个长方体纸盒,然后投影,让学生判断该纸盒是由图1中的哪种纸片折叠而成的.

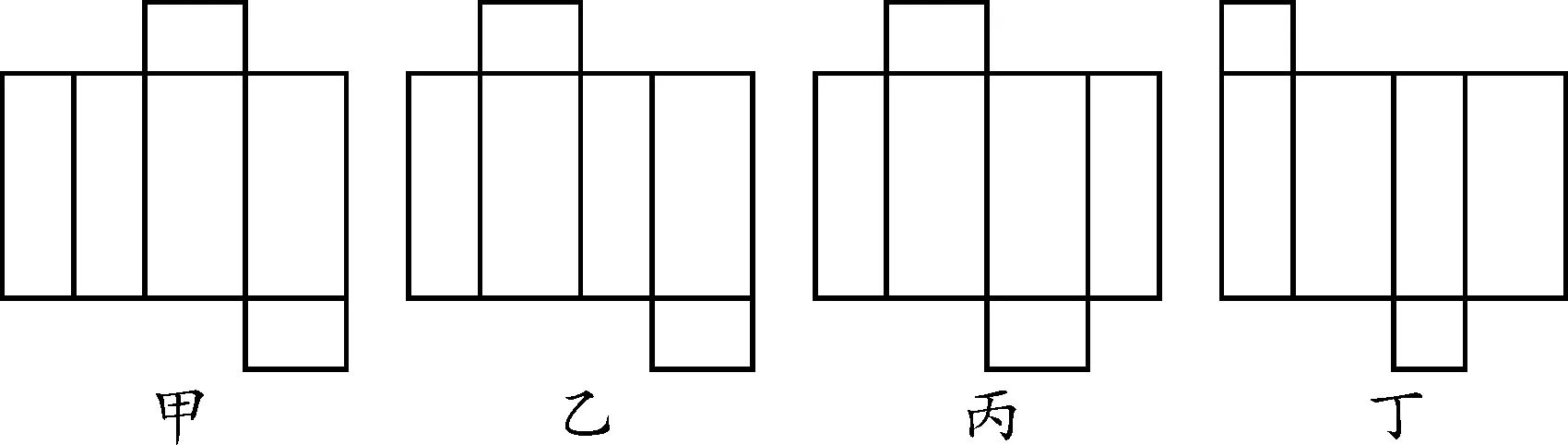
图1

创设目的:乍看是差不多的图形,该如何找出折叠的规律?为学生的思维指明方向.

(3)启发学生运用数学概念与规律去释疑

存疑只是引起思考,真正目的还在于能用正确的方法释疑,因此,启发学生就需要驱动他们学会思考.对于数学问题,如果只凭经验和想当然作出判断,这是不好的思维习惯.因为数学是从生活中抽象出的“缜密”的模型,数学概念与规律是科学的.因此,应用数学概念与规律是解决数学问题的前提.如学习两直线位置关系时,判断“垂直于同一条直线的两条直线平行”,显然这是一个错误的命题,前提必须“在同一平面内”,这就要求对数学概念要有清晰的理解.

3 启发式教学的重要环节设置

启发式教学没有具体的模式,其重要环节在于质疑情境的创设与引导.从近年来课题组听课、评议的记录可以看出,具有多年经验的教师驾驭课堂的有些做法确实是“他山之石”.

(1)通过数学实验模拟的方法进行启发

数学是自然的科学,大量的数学模型都是通过实验抽象出来的.进行数学实验既是学科本身的需要,也是数学教学的需要.实验操作能够吸引学生的注意力,数据或模型能让抽象问题形象化,真正体现“数形结合”的思想.如八年级上册第三章第一节对勾股定理的证明,一位老教师的课堂实录片段如下:

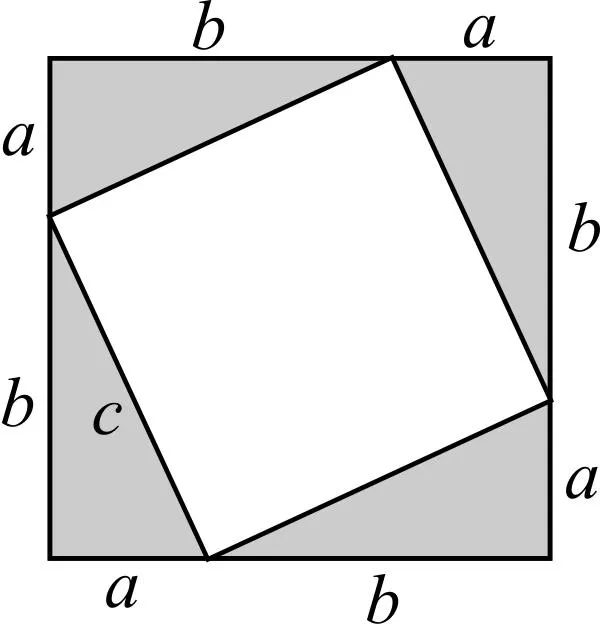
教师创设:拿出四个相同的直角三角形(直角边为a,b且a

图2

问题你能用两种方法求图2的面积吗?对比两种不同的表示方法,你能发现什么?

学生演算,说出结果.

教师引导:这个结果就是“勾股定理”.请同学们分组,再动手拼一拼,看看是否还有其他方法能得出直角三角形中的“勾股定理”.

学生分组进行实验,展示小组得出的成果.

课题组评议:教师将数字转化为正方形的面积,体现了“数形结合”思想.通过实验的方法,引起学生更深层次的思考,达到了教学的预期目的.

(2)利用由浅入深逐步递进的方法进行启发

数学建模是对知识由浅入深理解的过程,从初中数学知识的模块来看,每一章下设的几节内容都是递进的关系,甚至中考试题的设置也是“逐步递进”的.数学素养的养成也是循序渐进的过程.因此,在课堂教学中要通过精心的创设和启发,才能逐步达到活化思维的高度.下面是一位教师中考备考解法指导课的实录片段:

问题情境如图3,在正方形ABCD中,E为边BC上一点(不与点B,C重合),垂直于AE的一条直线MN分别交AB,AE,CD于点M,P,N.判断线段DN,MB,EC之间的数量关系,并说明理由.

图3

(教师点评,学生探究.)

问题探究:在“问题情境”的基础上.

如图4所示,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交AD于点F．求∠AEF的度数;

图4

课题组评议:采用2021年江苏连云港市中考卷的第27题,目标明确.直接用原题中的问题情境创设课堂教学情境,“借力打力”,匠心独运.然后让学生独立完成问题探究,为中考备考知识建模夯实了基础.

总之,在数学教学中引导思考,启发式教学的方法是多角度、多元化的.以上案例解读是近年来课题组在活动过程中的总结.只有在数学课堂教学中将激发学生的存疑作为出发点,将驱动存疑、探疑与释疑作为目标,缜密设置重要的教学环节,那么,启发式教学过程定会有广阔的天地和可开拓的空间.