多孔结构对冲击波的衰减影响研究

黄 浩,崔海林,田晓丽,吴 浩

(1.中北大学机电工程学院,山西 太原 030051)(2.中国兵器工业第二〇八研究所瞬态冲击技术重点实验室,北京 102202)

21世纪以来,弹药爆炸造成的单兵战斗伤亡比例持续上升,爆炸产生的碎片和复合冲击波已成为主要的伤害来源[1]。爆炸是含能材料在短时间内转化为高温高压气体并释放大量能量的过程[2-4]。头盔是军人战斗保护的重要装备,多孔材料作为一种具有优异能量吸收性能和轻质特性的材料,已被广泛应用于头盔内衬的设计中。Mourtize[5]采用理论和实验验证相结合的方法,对高分子多孔结构材料的抗爆性能进行了深入研究。王永刚等[6]则通过理论和实验,分析了冲击波在轻质多孔结构材料中的传播规律。王海福等[7]认为多孔材料中初始冲击波随孔隙度的增加而下降。宋博、胡时胜等[8-9]进行了动态压缩实验,提出了多孔材料在冲击载荷作用下破坏波(压实波)的概念。前人研究表明,多孔材料具有优异的能量吸收性能和轻质特性,能够有效减缓冲击波,但是主要集中在材料的制备、性能表征和实验测试等方面。因此,本文采用数值模拟的方法定量研究了多孔结构几何参数对冲击波衰减的影响,对于优化多孔结构设计和提高其抗冲击性能具有重要意义。

1 数值仿真计算

1.1 数值模型

选用有限元分析软件AUTODYN,对球形装药爆炸冲击波场的形成和传播过程进行模拟,选用AUTODYN-2D模拟爆炸冲击波对多孔材料的冲击过程。除对称面外,空气域各边界设置“Flow-out”边界条件,实现Euler场边界能量的流出。Euler空气域网格选用单一尺寸为0.1 mm×0.1 mm,空气域尺寸为100 mm×4 mm,总网格数为40 000,通过填充方式将TNT材料填充到Euler区。多孔结构网格尺寸为0.1 mm×0.1 mm,长度为2 mm。

二维仿真模型如图1所示,考虑数值模拟的计算时间以及结构的对称性,采用1/2模型。

图1 二维仿真模型

为了得到爆炸冲击波冲击多孔结构时空气域中的压强,在Euler空气域中设置高斯点,如图2所示。本文数值模拟所涉及到的TNT材料、AIR材料、多孔材料,全部从AUTODYN材料库中调用。

图2 高斯点的分布

1.2 材料模型

空气采用理想气体状态方程描述:

p1=(γ-1)ρe+pshift

(1)

式中:p1为压力,e为比热力学能,γ为多方指数,pshift为压力偏移量,ρ为密度。对于式(1),在mm-mg-ms单位制下,分别取γ、ρ、e为1.4、1.255 J/mg、2.068×105mg/mm3。

采用JWL状态方程描述TNT材料:

(2)

式中:p2为爆轰压力,E为初始热力学能,η为爆轰产物的体积比,A为流体的体积压缩性参数,B为流体的容积相关性参数,ω为压缩应变,R1、R2为流体的热压耦合系数。

TNT材料状态方程参数见表1,多孔结构材料参数见表2。

表1 TNT材料状态方程参数

表2 多孔结构材料参数

1.3 理论模型

爆炸冲击波不仅沿着横向传播而且也沿着纵向传播,当冲击波垂直碰撞目标时,冲击波的强度在垂直方向相比长度方向要小,并且多孔材料在压缩过程中,其泊松比 0,即多孔材料只在横向上产生压缩或者在垂直方向上的变形量几乎为0[10]。因此对多孔结构所受冲击载荷的计算可以简化为一维应力波在多层介质中传播规律的理论计算。

当爆炸冲击波在不同材料介质中传播时,由于各层材料的冲击波阻抗不同,冲击波在两层材料的分界面产生透射波和反射波,由分界面的连续条件可知分界面处的压力、质点速度相等,分界面两边的透射波和反射波的强度分别为[11]

(3)

(4)

式中:σT2为第2层材料的透射波强度,σR1为第1层材料的反射波强度,σ1为入射应力波强度,ρ1、ρ2分别为第1层、第2层材料的密度,c1、c2分别为第1层、第2层材料的弹性波波速,ρ1c1和ρ2c2分别为两层材料的波阻抗。其透射波系数T和反射波系数R分别为:

(5)

(6)

对于入射波以压缩纵波冲击目标时,综合分析式(3)～(6)可得:

1)当波由波阻抗较小的介质传入波阻抗较大的介质时,有ρ1c1<ρ2c2,由式(6)可得R>0。由式(3)、(4)可知,反射波和入射波的应力方向相同(反射加载),由式(5)可得T>1,即透射波的幅值大于入射波。

2)当波由波阻抗较大的介质传入波阻抗较小的介质时,有ρ1c1>ρ2c2,由式(6)可得R<0。由式(3)、(4)可知,反射波和入射波的应力方向相反(反射卸载),由式(5)可得T<1,即透射波的幅值小于入射波。

当冲击波经过多孔结构时,波循环由波阻抗较小的空气传入波阻抗较大的多孔结构、再由波阻抗较大的多孔结构传入波阻抗较小的空气,由理论分析可知,多孔结构能够有效地减弱波的强度。冲击波在孔隙结构中传播,由于波阻抗的不同,孔隙结构通过部分反射和部分吸收冲击波能量,因而具有降低冲击波强度的效果。

2 仿真结果与分析

为研究多孔结构对冲击波衰减的影响,以不同孔径和不同孔隙率的多孔结构作为研究对象,通过仿真模拟的方法,分析其变形吸能过程并对比Euler空气域中高斯点1、2处的最大压强,以不同参数下多孔结构的吸能值和相同冲击载荷下多孔结构的压缩距离为参考来评估其对冲击波的衰减程度。

相同孔径不同孔隙率多孔结构相关参数,见表3。

表3 相同孔径不同孔隙率多孔结构相关参数

相同孔隙率不同孔径多孔结构相关参数,见表4。

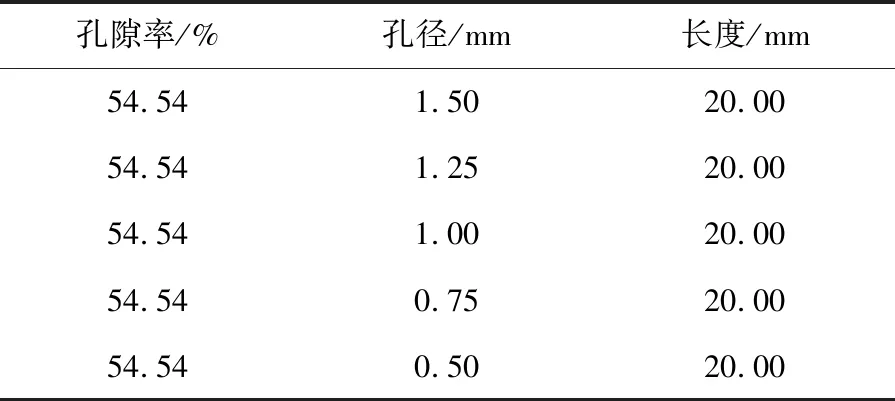
表4 相同孔隙率不同孔径多孔结构相关参数

2.1 多孔结构的变形吸能过程

在冲击载荷作用的初期,多孔结构的骨架发生弹性变形,孔隙被轻微压缩,如图3(a)所示,但由于骨架材料的弹性模量较高,导致多孔材料吸收的能量也较少。当冲击波进一步作用于多孔材料的单元壁时,由于冲击载荷增大,使得空腔内部气体压缩产生的反向压力和冲击波压力之间不平衡,发生屈曲现象。屈曲是指结构在轴向压缩载荷作用下发生的失稳变形现象,其是一种弹性失稳现象。屈曲可以有效地降低多孔材料的刚度,增加其变形量,此时冲击波能量的消耗也随之增加。图3(b)显示了多孔材料圆形空腔单元在冲击波作用下的屈曲过程,由图可知,随着时间的推移,空腔单元壁逐渐发生屈曲变形,其最大位移和最大应变都显著增加。

图3 屈曲变形状态

随着冲击载荷增加，多孔材料的骨架发生塑性变形，孔隙被进一步压缩，即骨架在超过其屈服强度后发生不可恢复的变形。塑性变形可以有效地降低多孔结构的强度，增加其损伤范围，从而消耗冲击波能量。在这个阶段，骨架材料的塑性变形较大，吸收的能量较多。图4显示了多孔材料圆形空腔单元在冲击波作用下的塑性变形过程，从图中可以看出，随着时间的推移，空腔单元壁逐渐发生塑性变形，其最大应力和最大塑性应变都显著增加。

图4 多孔材料的塑性变形

当冲击载荷继续增加时,多孔材料的骨架发生严重的塑性变形和损伤,孔隙被大幅度压缩,甚至达到致密化状态。在这个阶段,多孔材料的应力-应变曲线急剧上升,骨架损伤严重,吸收的能量也大幅度增加。图5显示了多孔材料圆形空腔单元在冲击波作用下的致密过程。从图中可以看出,随着时间的推移,空腔单元达到致密化状态,在这个阶段骨架损伤严重,单个完整胞元在未断裂之前其变形达到最大。

图5 多孔材料致密过程

随着冲击载荷进一步增加,多孔材料的单元壁在冲击波作用下,受到高强度和高速度的载荷作用,发生断裂。断裂可有效降低多孔结构的完整性,增加其碎片数量,从而消耗冲击波能量。图6显示了多孔材料圆形空腔单元在冲击波作用下的断裂过程,从图中可以看出,随着时间的推移,空腔单元壁逐渐发生断裂,其最大应力和最大损伤因子都显著增加。

图6 多孔材料的断裂过程

2.2 不同孔隙率及孔径对冲击波的衰减影响

表5列出了在相同冲击载荷作用下不同孔隙率(40.07%、46.47%、50.27%、54.54%、59.38%、64.9%)、不同孔径(0.50 mm、0.75 mm、1.00 mm、1.25 mm、1.50 mm)下的多孔结构前后空气域的最大压强。因为是同一冲击波作用,所以高斯点1处的压强完全一样。由表5可知,高斯点2处的压强几乎都保持在一个标准大气压,表明多孔结构可以有效地减少爆炸冲击波所产生的能量和压强。

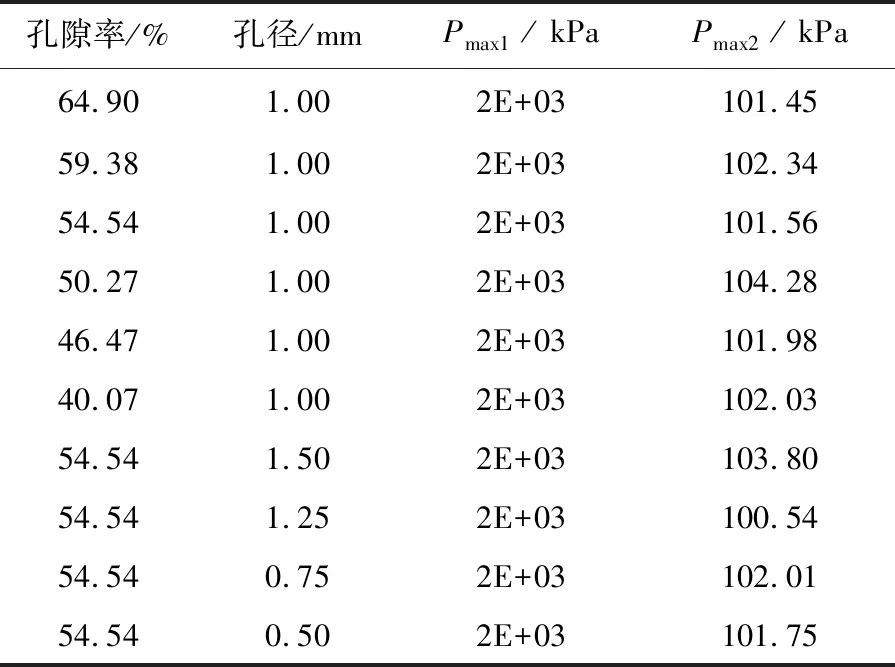
表5 不同结构下高斯点1、2处的最大压强Pmax1、Pmax2

图7、图8分别列出了不同孔隙率相同孔径、不同孔径相同孔隙率的多孔结构在相同冲击载荷作用下的吸能值随着时间变化曲线。对比图7孔隙率为40.07%、46.47%、50.27%所对应的曲线可知,随着多孔结构孔隙率的增加,其吸能值也在进一步增加,当多孔材料的孔隙率增加到一定值时(如图7孔隙率为50.27%、54.54%所对应的曲线),其吸能值差别较小,可以认为在一定孔隙率范围内增大孔隙率,多孔材料的吸能值趋于稳定;随着孔隙率的继续增加(如图7孔隙率为59.38%、64.90%所对应的曲线),多孔结构的吸能值会有所减小,主要是因为在孔径和长度不变时,随着孔隙率的增加,会使其胞元个数增加,致使骨架壁厚减少,从而导致其抵抗冲击波的能力减弱,加快多孔结构的断裂。

图7 不同孔隙率下多孔结构的吸能值随时间变化的曲线

图8 不同孔径下多孔结构的吸能值随时间变化的曲线

对比图8孔径为0.50 mm、0.75 mm、1.00 mm所对应的曲线可知,当孔隙率一定时,多孔结构的吸能值与其孔径的大小成正比,即随着孔径的增加,多孔结构的能量吸收能力逐渐提高,但当孔径继续增加,超过1.00 mm时,其吸能值明显降低,这是因为在多孔结构长度一定的情况下,为保证相同的孔隙率,增大单个胞元的孔隙必然会导致多孔结构横向胞元数量减少,从而减弱其吸能效果。由此可知,适当增加多孔结构的孔径可以有效提高其吸能效果。

表6列出了同一冲击载荷不同结构参数下多孔结构的压缩距离。由表可知,在相同冲击载荷作用下,随着孔隙率的增加其压缩距离也在增加,这也从侧面说明了多孔结构对冲击波的衰减程度与孔隙率成正比,如表6孔隙率为50.27%、54.54%所对应的压缩距离所示,当孔隙率继续增加,压缩距离增长缓慢,表明其吸能值趋于稳定,当孔隙率超过这一范围(50.00%～55.00%)后,压缩距离明显减小。由表6孔隙率为54.54%,孔径分别为0.50 mm、0.75 mm、1.00 mm、1.50 mm、1.75 mm所对应的压缩距离可知,当孔隙率一定时,压缩距离随着孔径的增大而增大,说明其吸能值随着孔径的增大而增大,但当孔径大于1.00 mm时,其吸能效果将会减弱。

表6 不同结构参数多孔材料的压缩距离

3 结束语

本文通过数值模拟分析,探究不同孔隙率和不同孔径下的多孔结构对冲击波的衰减影响和吸能特性,得出以下结论:

1)多孔结构作为头盔内衬能够有效衰减冲击波,降低爆炸冲击波对头部的伤害。孔径和孔隙率的变化对能量吸收性能有一定影响,适当增加孔径和增大孔隙率能够提高其能量吸收能力。

2)当孔径一定时,随着孔隙率的增加,多孔结构的吸能能力也逐渐提高,但当孔隙率增加到一定范围即50.00%～55.00%时,吸能能力趋于稳定,超出这一范围后多孔结构的吸能能力与其孔隙率呈负相关。

3)相同孔隙率下,随着孔径增加,多孔结构的能量吸收能力逐渐增加,但当孔隙率增加超过1.00 mm后,吸能能力反而减弱。